PHYSICS CHAPTER 5 WORK ENERGY WORK AND ENERGY














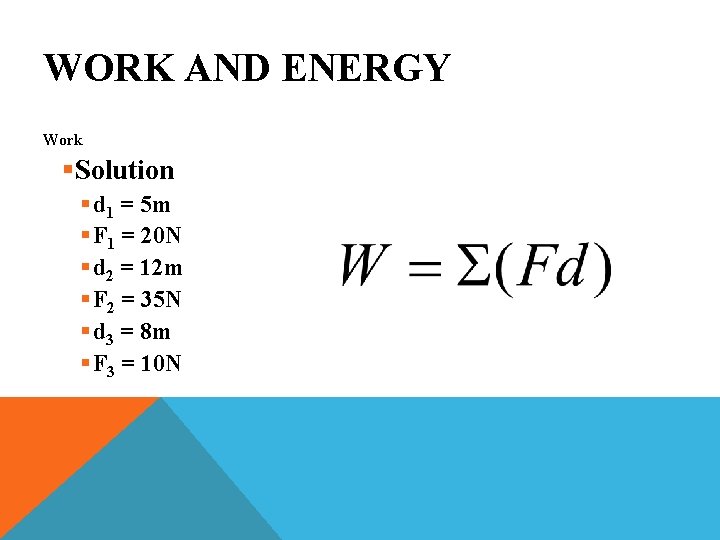








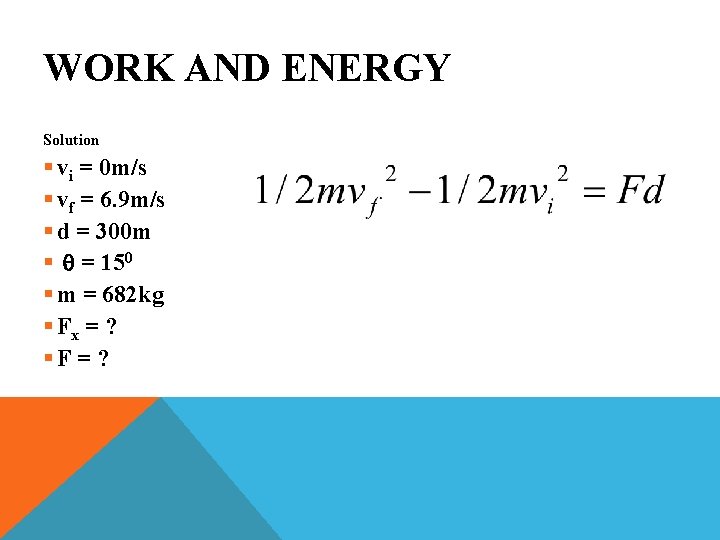

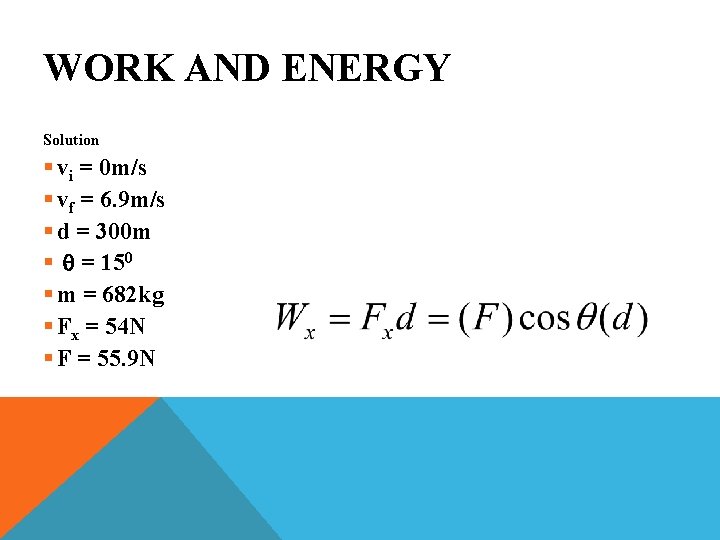
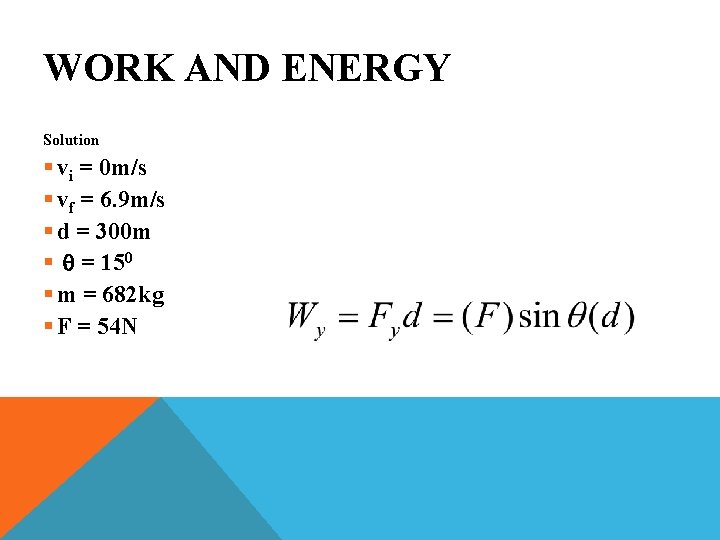
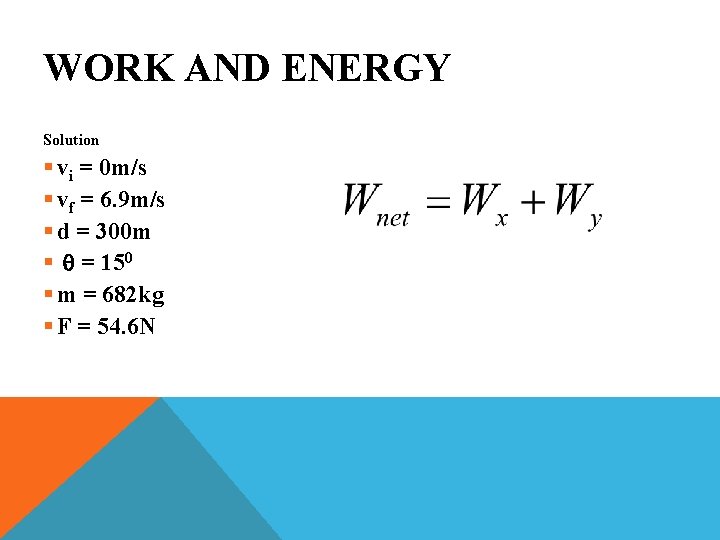




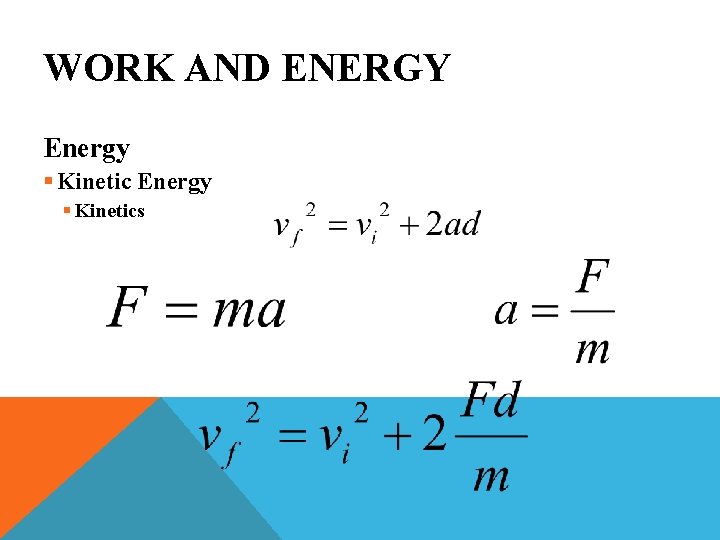
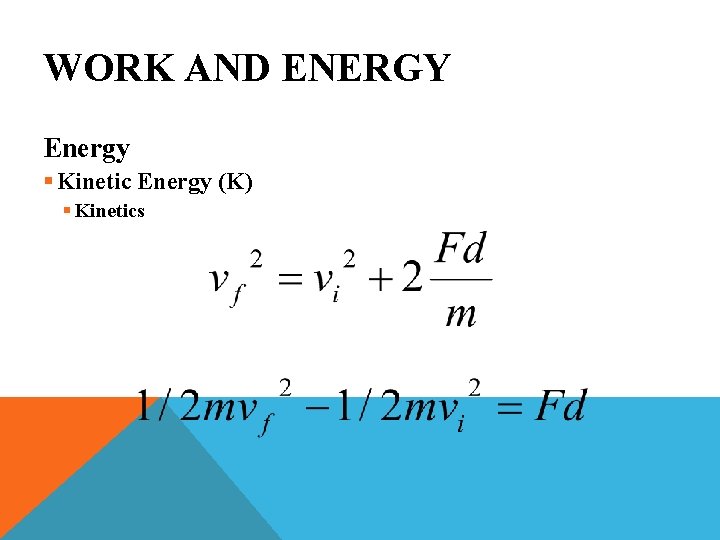












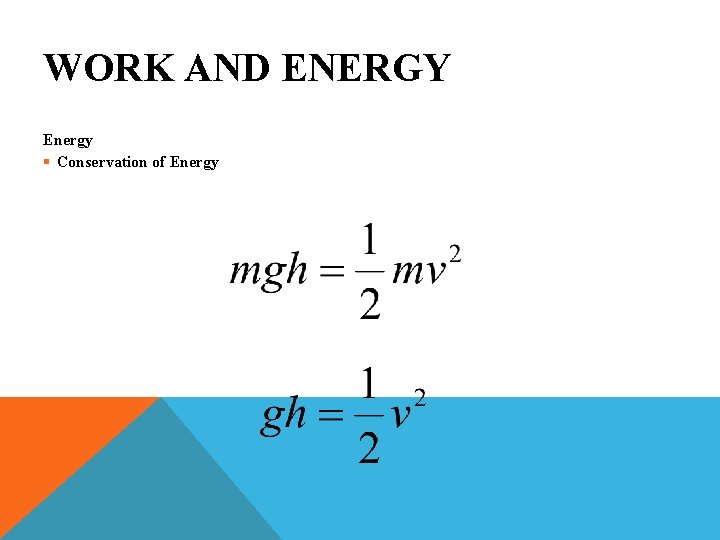
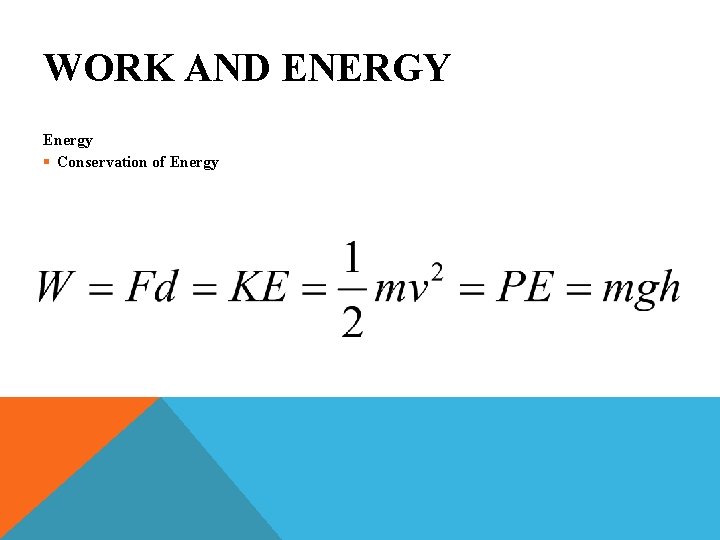


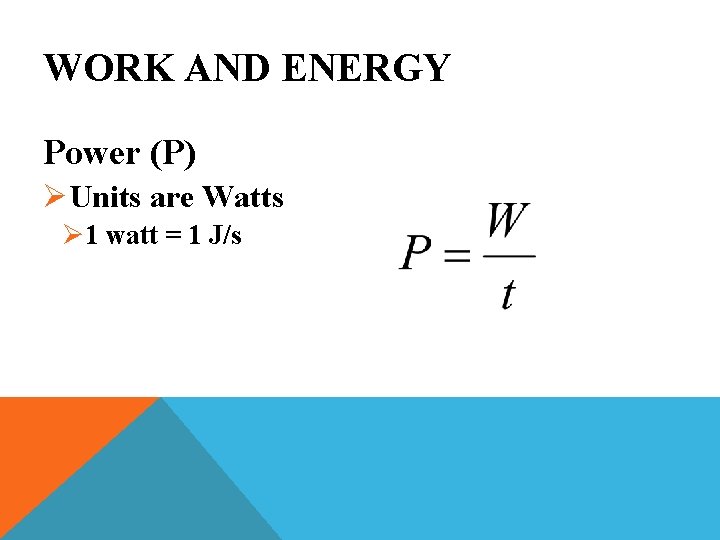

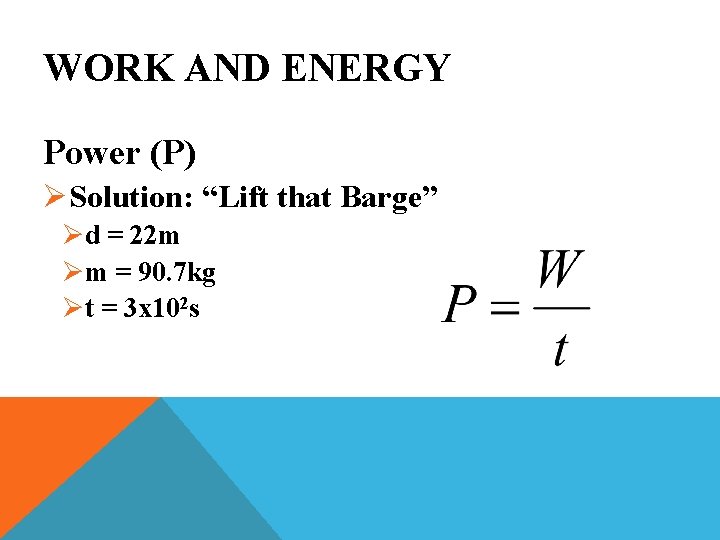

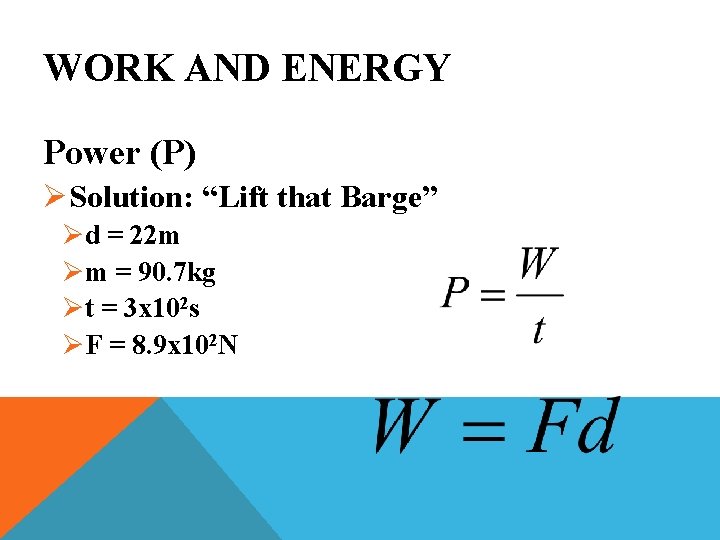


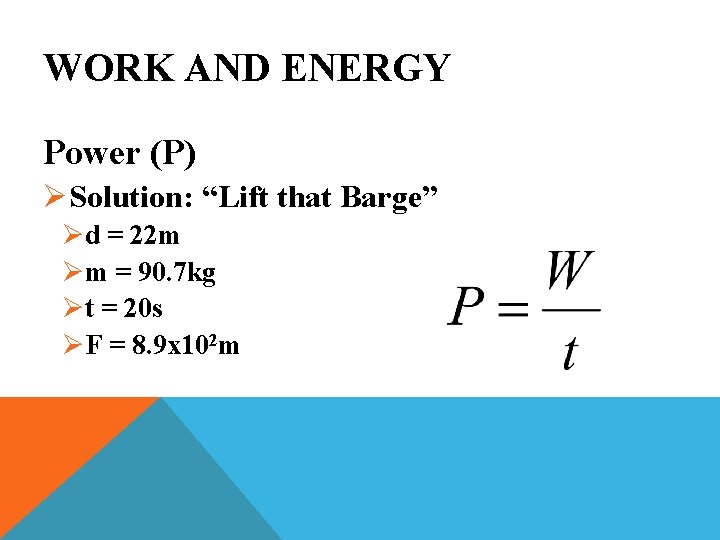


















- Slides: 83

PHYSICS CHAPTER 5: WORK & ENERGY

WORK AND ENERGY Work §A Force that Causes the Displacement of an Object Does Work on the Object

WORK AND ENERGY Work §Has Direction (+ or -) §May Increase Energy of the System (+) §May Decrease Energy of the System (-)

WORK AND ENERGY Work §Units §Force – Newton (kg*m/s 2) §Displacement – Meter §Work – Joule (kg*m 2/s 2) – (Nm)

WORK AND ENERGY Work §A Horizontal Component of the Force (Relative to Motion) Must Do the Work

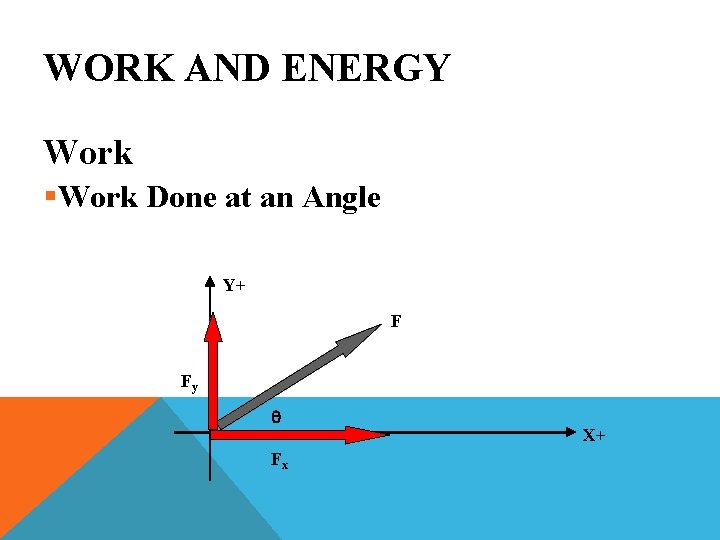
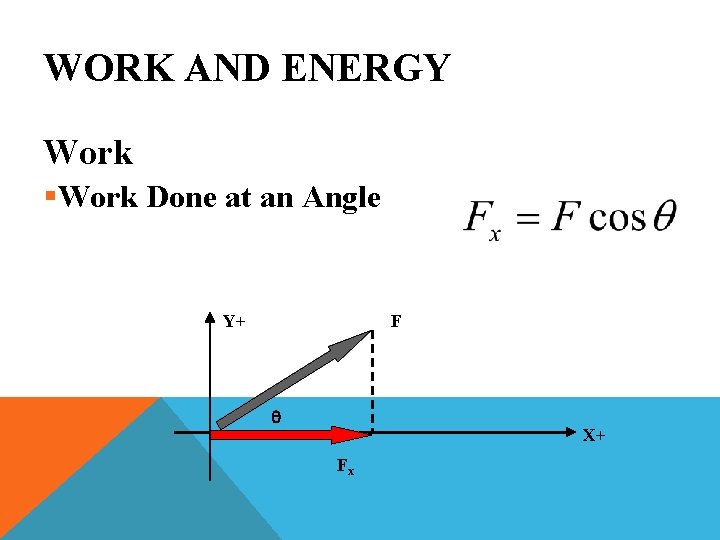
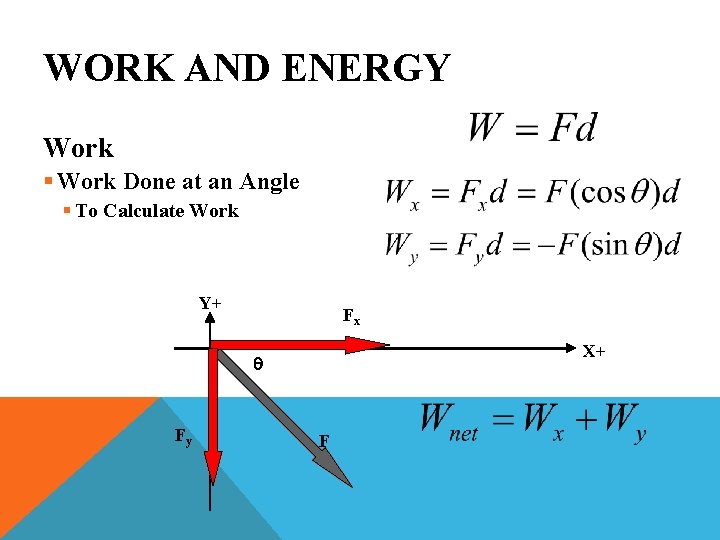
WORK AND ENERGY Work § Work Done at an Angle § Forces Only Move in One Direction, but Involve 2 Axis § These Axis Vectors Can Be Separated and Calculated Individually Y+ F X+

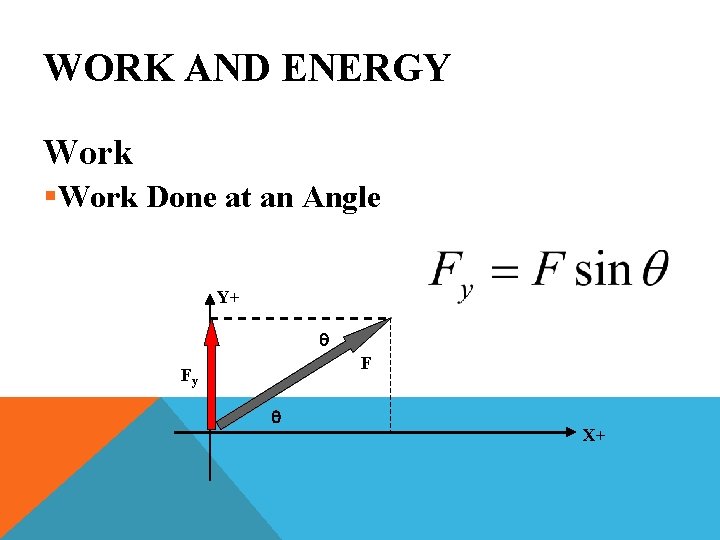
WORK AND ENERGY Work §Work Done at an Angle Y+ F Fy q Fx X+

WORK AND ENERGY Work §Work Done at an Angle Y+ F q X+ Fx

WORK AND ENERGY Work §Work Done at an Angle Y+ q F Fy q X+

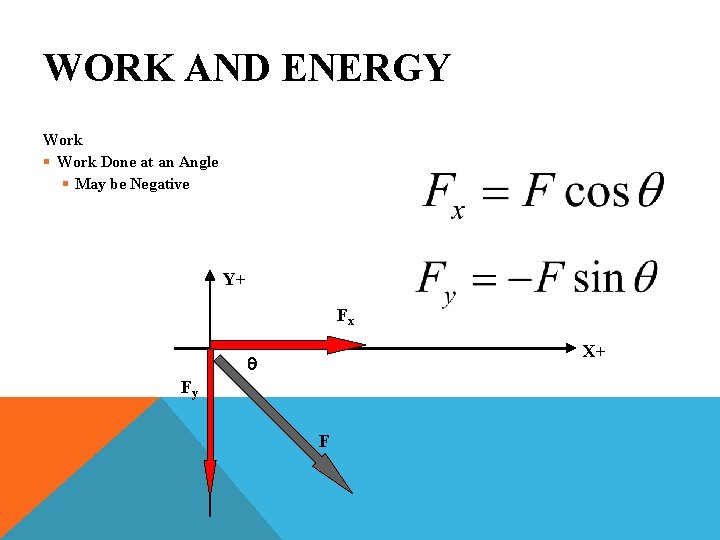
WORK AND ENERGY Work § Work Done at an Angle § May be Negative Y+ Fx X+ q Fy F

WORK AND ENERGY Work § Work Done at an Angle § To Calculate Work Y+ Fx X+ q Fy F

WORK AND ENERGY Work §Problem “Work Truck” §m = 2800 kg §F = 29 N §d = 500 m §What is W? Y+ d X+

WORK AND ENERGY Work §Solution §m = 2800 kg §F = 29 N §d = 500 m Y+ d X+

WORK AND ENERGY Work §Problem “Building Moving” § m = 6600 kg § d = 2. 5 m §What is the Amount of Work?

WORK AND ENERGY Work §Solution “Building Moving” § m = 6600 kg § d = 2. 5 m

WORK AND ENERGY Work §Solution “Building Moving” § m = 6600 kg § d = 2. 5 m § F = 6. 5 x 104 N

WORK AND ENERGY Work §Problem § The third floor of a house is 8 m above street level. How much work is needed to move a 150 kg refrigerator to the third floor?

WORK AND ENERGY Work §Solution § d = 8 m § m = 150 kg

WORK AND ENERGY Work §Problem § John pushes a box across the floor of a stage with a horizontal force. The roughness of the floor changes, and John must exert a force of 20 N for 5 m, then 35 N for 12 m, then 10 N for 8 m. What is the work that John has done pushing the box?
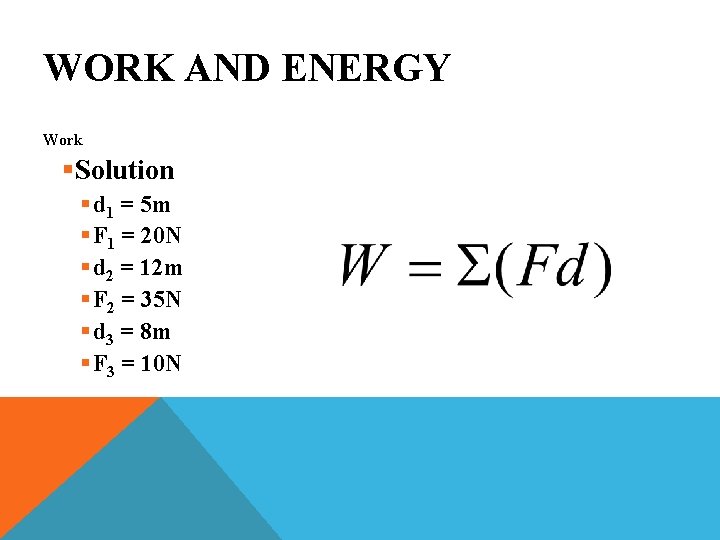
WORK AND ENERGY Work §Solution § d 1 = 5 m § F 1 = 20 N § d 2 = 12 m § F 2 = 35 N § d 3 = 8 m § F 3 = 10 N

WORK AND ENERGY Work §Solution

WORK AND ENERGY Work §Problem § A pump delivers 0. 55 m 3 of oil into barrels on a platform 25. 0 m above the pump intake pipe. The density of the oil is 0. 82 g/cm 3. What is the work done by the pump?

WORK AND ENERGY Work §Solution § d = 25. 0 m § volume = 0. 55 m 3 § density = 0. 82 g/cm 3 § mass = ?

WORK AND ENERGY Work §Solution § d = 25. 0 m § volume = 0. 55 m 3 § density = 0. 82 g/cm 3 § mass = ?

WORK AND ENERGY Work §Solution § d = 25. 0 m § volume = 0. 55 m 3 § density = 0. 82 g/cm 3 § mass = 4. 5 x 102 kg §F = ?

WORK AND ENERGY Work §Solution § d = 25. 0 m § volume = 0. 55 m 3 § density = 0. 82 g/cm 3 § mass = 4. 5 x 102 kg § F = 4. 4 x 103 N

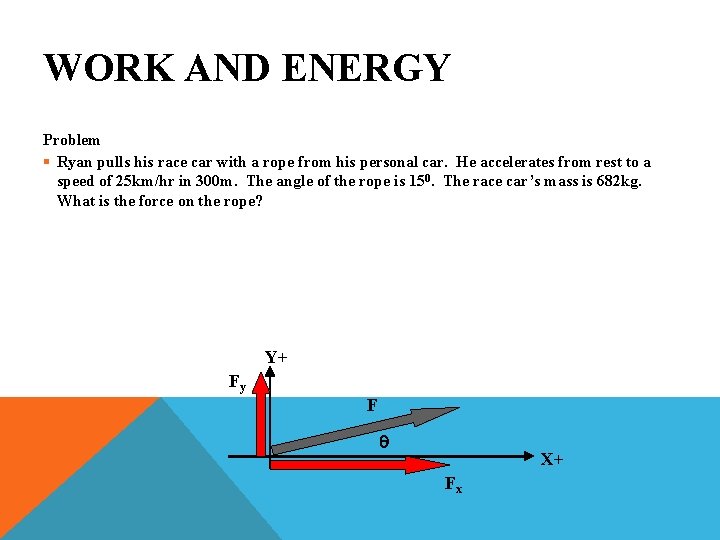
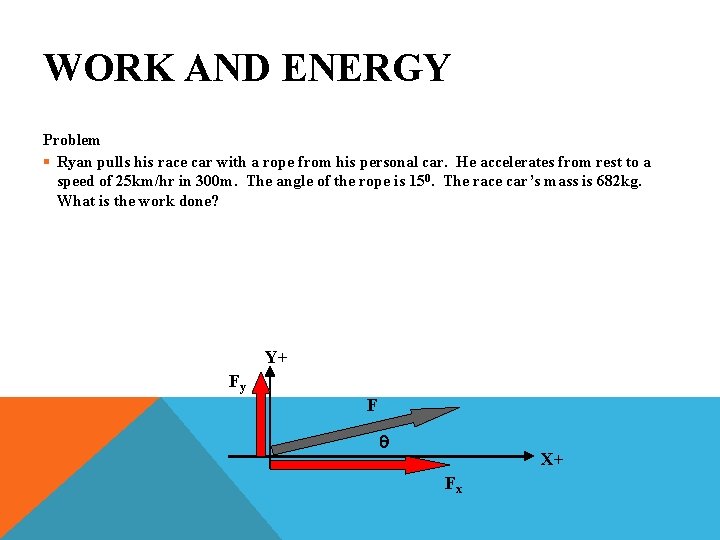
WORK AND ENERGY Problem § Ryan pulls his race car with a rope from his personal car. He accelerates from rest to a speed of 25 km/hr in 300 m. The angle of the rope is 150. The race car’s mass is 682 kg. What is the force on the rope? Y+ Fy F q X+ Fx

WORK AND ENERGY Solution § 25 km/hr § d = 300 m § q = 150 § m = 682 kg § Fx = ? §F = ?

WORK AND ENERGY Solution § vo = 0 m/s § vf = 6. 9 m/s § d = 300 m § q = 150 § m = 682 kg § Fx = ? §F = ?
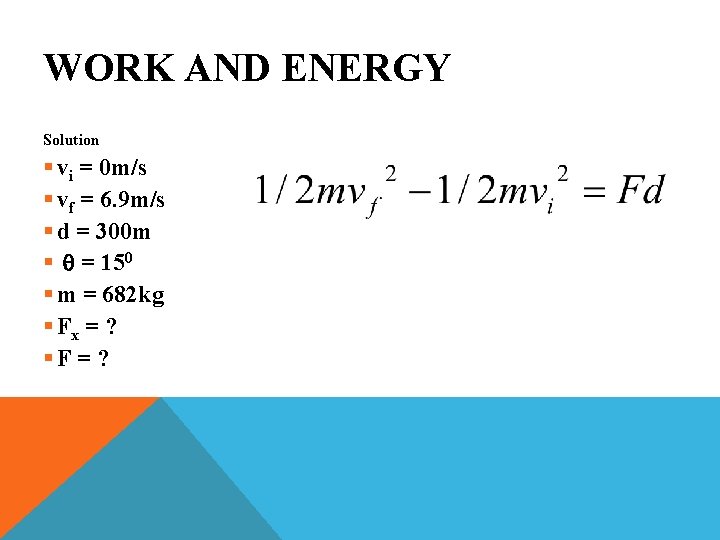
WORK AND ENERGY Solution § vi = 0 m/s § vf = 6. 9 m/s § d = 300 m § q = 150 § m = 682 kg § Fx = ? §F = ?

WORK AND ENERGY Solution § vi = 0 m/s § vf = 6. 9 m/s § d = 300 m § q = 150 § m = 682 kg § Fx = 54 N §F = ?

WORK AND ENERGY Problem § Ryan pulls his race car with a rope from his personal car. He accelerates from rest to a speed of 25 km/hr in 300 m. The angle of the rope is 150. The race car’s mass is 682 kg. What is the work done? Y+ Fy F q X+ Fx
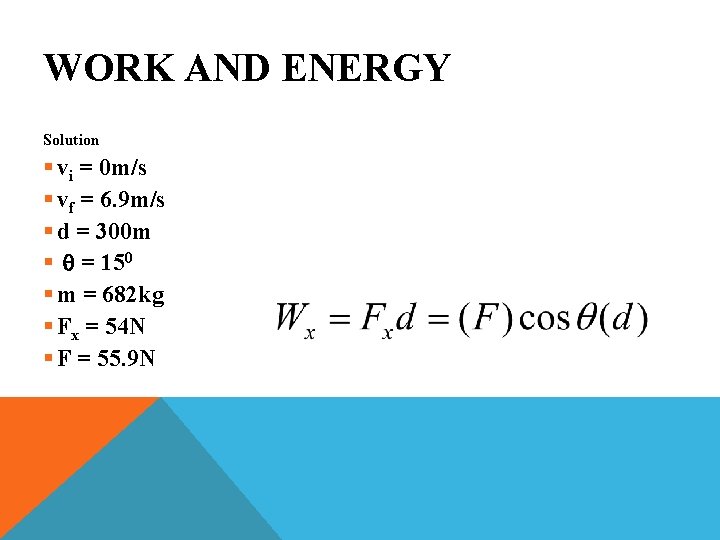
WORK AND ENERGY Solution § vi = 0 m/s § vf = 6. 9 m/s § d = 300 m § q = 150 § m = 682 kg § Fx = 54 N § F = 55. 9 N
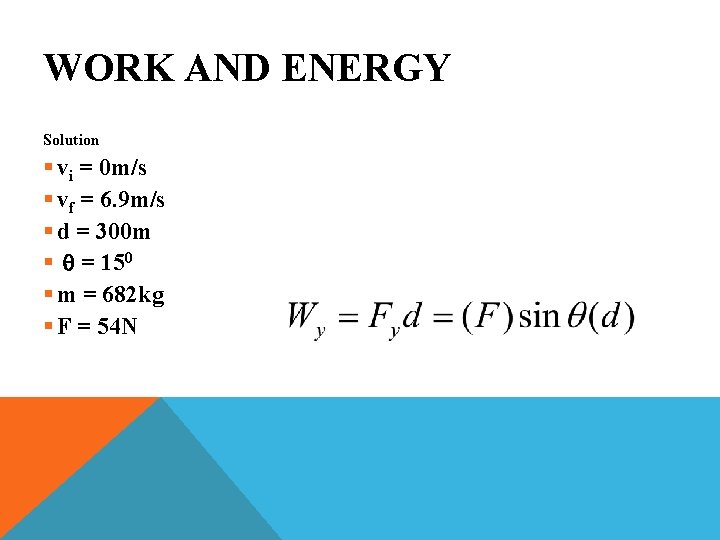
WORK AND ENERGY Solution § vi = 0 m/s § vf = 6. 9 m/s § d = 300 m § q = 150 § m = 682 kg § F = 54 N
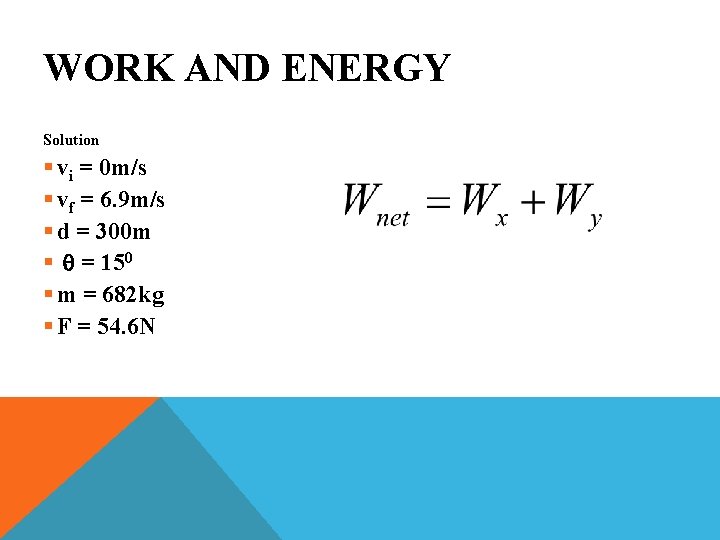
WORK AND ENERGY Solution § vi = 0 m/s § vf = 6. 9 m/s § d = 300 m § q = 150 § m = 682 kg § F = 54. 6 N

WORK AND ENERGY Energy §The Ability to Produce Change Within a System §Thermal Energy §Chemical Energy §Energy of Motion

WORK AND ENERGY Energy §Energy of Motion §The Energy of an Object Resulting from Motion §Kinetic Energy

WORK AND ENERGY Energy § Kinetics § Newton’s Second Law of Motion

WORK AND ENERGY Energy § Kinetics § Motion Equation § Vi is initial velocity § Vf is the final velocity § a is the instantaneous acceleration § d is the displacement
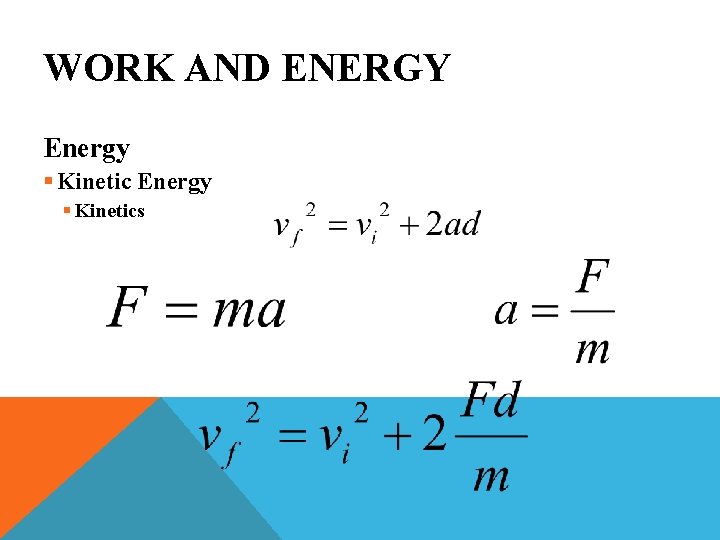
WORK AND ENERGY Energy § Kinetics
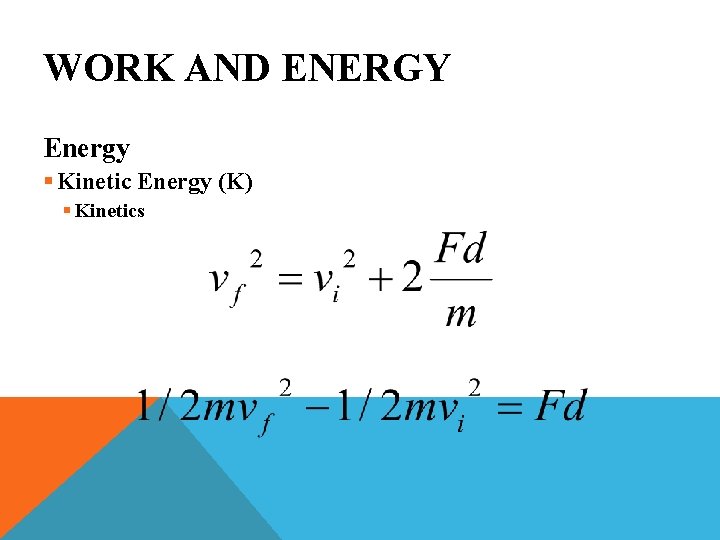
WORK AND ENERGY Energy § Kinetic Energy (K) § Kinetics

WORK AND ENERGY Energy § Kinetic Energy (K) § Kinetics Energy of the System = Environment

WORK AND ENERGY Energy § Kinetic Energy (K) § Kinetics System (Change in Energy) = Environment (Object) A Change in the Environment Due to Energy = Work

WORK AND ENERGY Energy § Kinetic Energy (K) § Kinetics A Change in the Environment Due to Energy = Work

WORK AND ENERGY Energy § Kinetic Energy (K) § Kinetics § Work-Energy Theorem

WORK AND ENERGY Energy §Kinetic Energy §Units §Joule (J) § 1 J=1 kg*m 2/s 2

WORK AND ENERGY Work §Problem “Work Truck” § m = 2800 kg § F = 29 N § d = 500 m §What is DKE? Y+ d X+

WORK AND ENERGY Work §Solution § m = 2800 kg § F = 29 N § d = 500 m Y+ d X+

WORK AND ENERGY Energy §Potential Energy (Gravitational) §Any Object Held by a Normal Force Against the Force of Gravity Contains Potential Energy

WORK AND ENERGY Energy §Potential Energy (Gravitational) §The product of… § the Mass of the Object § the Acceleration of Gravity § the Height of the Object

WORK AND ENERGY Energy §Potential Energy (Elastic)

WORK AND ENERGY Energy § Conservation of Energy § An Object’s Potential Energy is Equal to its Kinetic Energy When the Normal Force is Released

WORK AND ENERGY Energy § Conservation of Energy
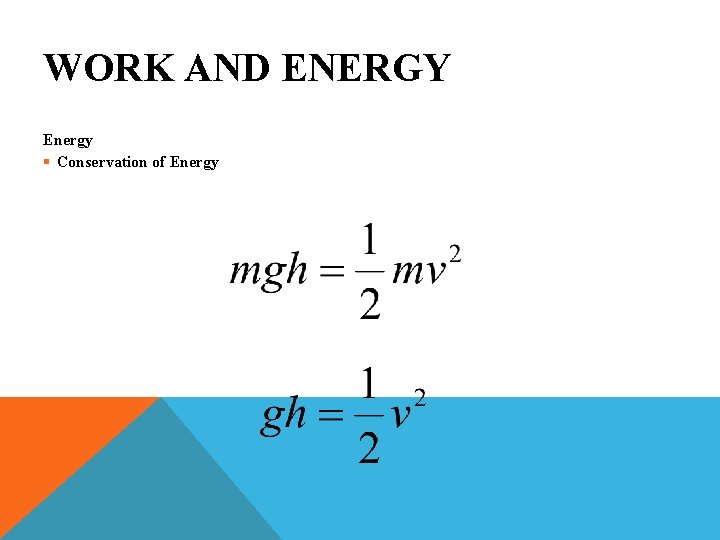
WORK AND ENERGY Energy § Conservation of Energy
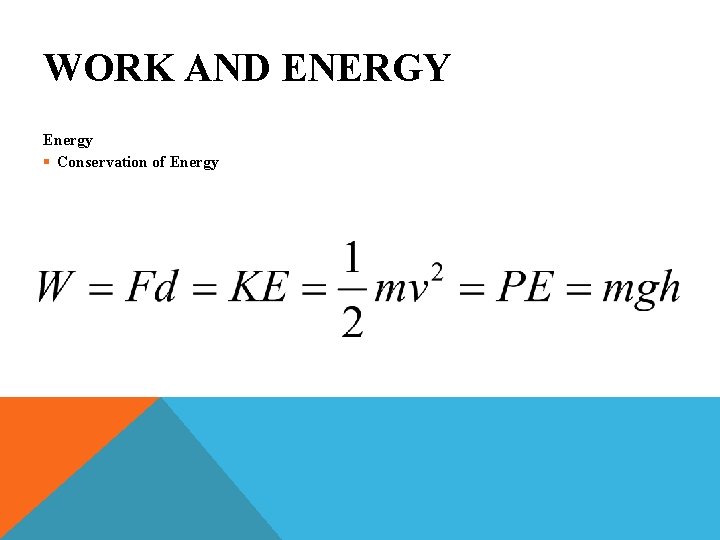
WORK AND ENERGY Energy § Conservation of Energy

WORK AND ENERGY Power §Work Can be Done Quickly, or… §The Same Work Can be Done Over a Long Period of Time §Power is the Rate of Doing Work (the rate of energy transferred)

WORK AND ENERGY Power (P) W = Work (Joules) t =Time (sec) “The Less Time, the Greater the Power”
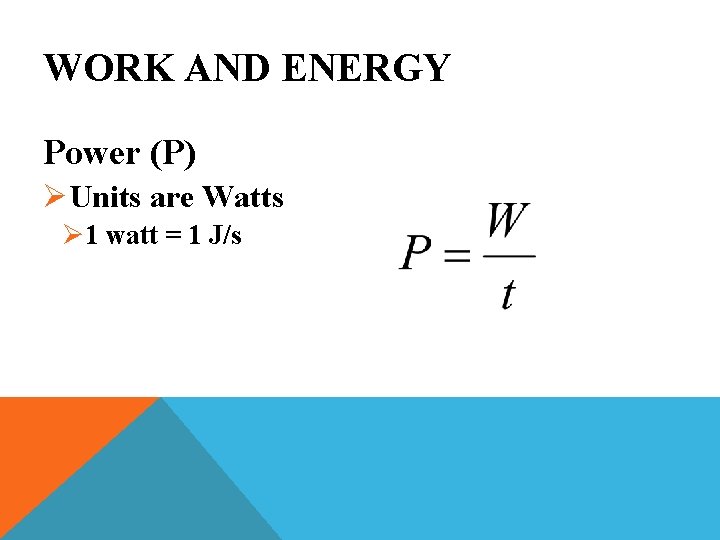
WORK AND ENERGY Power (P) ØUnits are Watts Ø 1 watt = 1 J/s

WORK AND ENERGY Power (P) ØProblem: “Lift that Barge” ØRyan Hauls His Piano Up Two Flights of Stairs (22 m) in 5 minutes. The Piano’s mass is 90. 7 kg. What Power is Used?
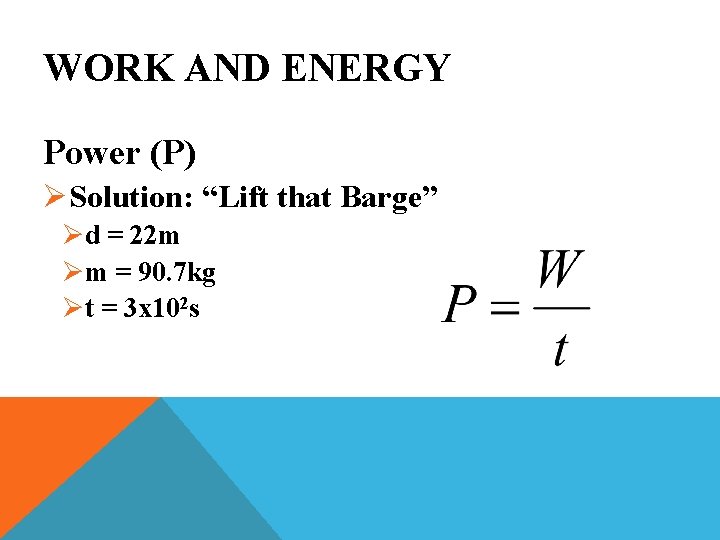
WORK AND ENERGY Power (P) ØSolution: “Lift that Barge” Ød = 22 m Øm = 90. 7 kg Øt = 3 x 102 s

WORK AND ENERGY Power (P) ØSolution: “Lift that Barge” Ød = 22 m Øm = 90. 7 kg Øt = 3 x 102 s
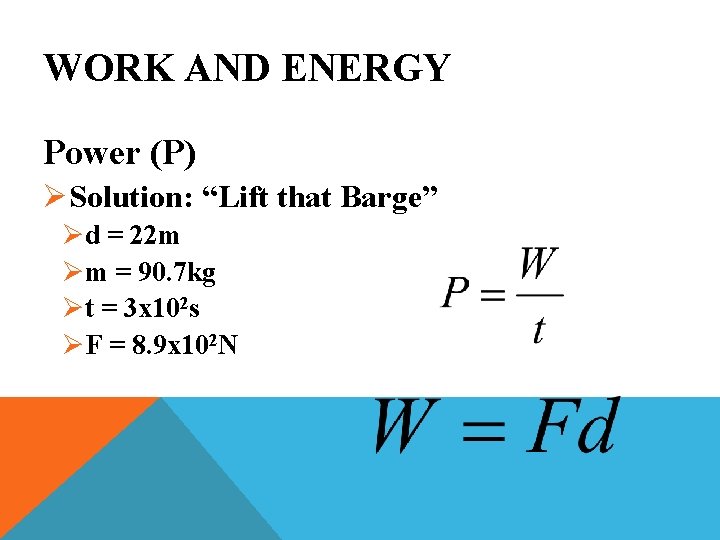
WORK AND ENERGY Power (P) ØSolution: “Lift that Barge” Ød = 22 m Øm = 90. 7 kg Øt = 3 x 102 s ØF = 8. 9 x 102 N

WORK AND ENERGY Power (P) ØSolution: “Lift that Barge” Ød = 22 m Øm = 90. 7 kg Øt = 3 x 102 s ØF = 8. 9 x 102 N

WORK AND ENERGY Power (P) Ø Problem: “Lift that Barge II” ØWhat If Ryan Hustled the Piano Up the Stairs in 20 seconds?
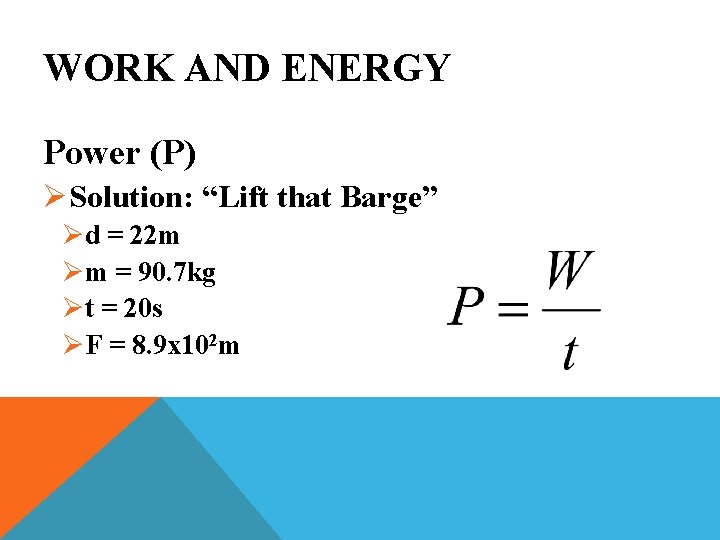
WORK AND ENERGY Power (P) ØSolution: “Lift that Barge” Ød = 22 m Øm = 90. 7 kg Øt = 20 s ØF = 8. 9 x 102 m

WORK AND ENERGY Power (P) ØSolution: “Lift that Barge” Ød = 22 m Øm = 90. 7 kg Øt = 20 s ØF = 8. 9 x 102 m

WORK AND ENERGY Power (P) Ø WOW! ØTo Move the Piano in 5 Minutes – 65 w ØTo Do the Same Work in 20 seconds – 979 w ØYes, 20 seconds is 1/15 of the original 5 minute time and 65. 3 x 15 = 979. Hey! A Direct Relationship!

WORK AND ENERGY Problem §A force of 300. 0 N is used to push a 145 -kg mass 30. 0 m horizontally in 3. 00 s. What is the power developed?

WORK AND ENERGY Solution §F = 300 N §d = 30. 0 m §m = 145 kg §t = 3. 0 s

WORK AND ENERGY Problem §April pushes a wheelbarrow by exerting a 145 N force horizontally. April moves it 60. 0 m at a constant speed for 25. 0 s. What power does April develop?

WORK AND ENERGY Solution §F = 145 N §d = 60. 0 m §t = 25. 0 s

WORK AND ENERGY Problem §If April moves the wheelbarrow twice as fast, how much power is developed?

WORK AND ENERGY Solution §F = 145 N §d = 60. 0 m §t = 12. 5 s

WORK AND ENERGY Problem §Jon pulls a 305 N sled along a snowy path using a rope that makes a 45. 0° angle with the ground. Jon pulls with a force of 42. 3 N. The sled moves 16 m in 3. 0 s. What power does Jon produce?

WORK AND ENERGY Solution §Fg = 305 N §F = 42. 3 N §d = 16. 0 m §t = 3. 0 s § q = 450

WORK AND ENERGY Problem §A lawn roller is pushed across a lawn by a force of 115 N along the direction of the handle, which is 22. 5° above the horizontal. If you develop 64. 6 w of power for 90. 0 s, what distance is the roller pushed?

WORK AND ENERGY Solution §F = 115 N §P = 64. 6 w §t = 90. 0 s § q = 22. 50

WORK AND ENERGY Problem §You slide a crate up a ramp at an angle of 30. 0° by exerting a 225 N force parallel to the ramp. The crate moves at constant speed. The coefficient of friction is 0. 28. How much work have you done on the crate when it is raised a vertical distance of 1. 15 m?

WORK AND ENERGY Solution §F = 225 N § mk = 0. 28 §h = 1. 15 m § q = 30. 00

WORK AND ENERGY Problem §An engine moves a boat through the water at a constant speed of 15 m/s. The engine must exert a force of 6. 0 x 103 N to balance the force that water exerts against the hull. What power does the engine develop?

WORK AND ENERGY Solution §F = 6. 0 x 103 N §v = 15 m/s

WORK AND ENERGY Problem §A 188 W motor will lift a load at the rate (speed) of 6. 50 cm/s. How great a load can the motor lift at this rate?

WORK AND ENERGY Solution §P = 188 W §v = 6. 5 cm/s = 0. 065 m/s