Physics bridging task 3 c Newtons second law

Physics bridging task 3 c: Newton’s second law (2). Continuing theme of consolidating material that you have already covered in Y 11, (so that you have a really firm foundation in GCSE physics when you start the A-level course), the following is the third of three Powerpoint presentations on Newton’s laws of motion. Work through the Powerpoint presentation, completing the included exercises, which are all capable of being self-marked. Because of this, you may work at your own pace, and set your own deadline, appropriate to your own circumstances.

Newton’s second law (2) From the previous lesson: To be able to describe an experiment to verify Newton’s second law. : to check whether it is true. Newton said that when something called a ‘force’ acts on a mass it will cause it to accelerate. Newton went further and suggested the relationship between the force, the mass it acts on and the resulting acceleration: Force α mass x acceleration directly proportional (this means to double the acceleration you needto double the force, if the mass stays the same. Force = mass x acceleration In our SI system of units, the relationship becomes: (N) (kg) (m/s 2)

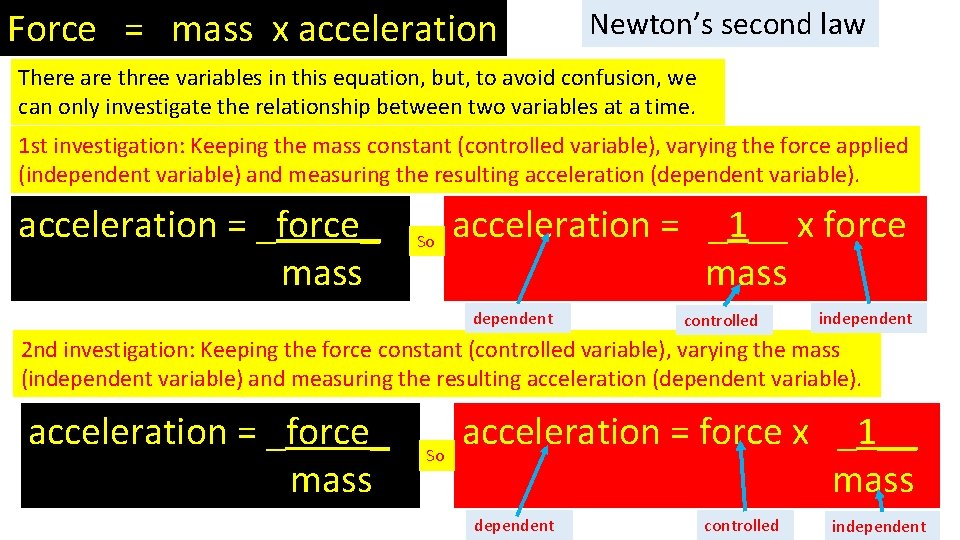
Force = mass x acceleration Newton’s second law There are three variables in this equation, but, to avoid confusion, we can only investigate the relationship between two variables at a time. 1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). acceleration = _force_ mass So acceleration = _1__ x force mass dependent controlled independent 2 nd investigation: Keeping the force constant (controlled variable), varying the mass (independent variable) and measuring the resulting acceleration (dependent variable). acceleration = _force_ mass So acceleration = force x _1__ mass dependent controlled independent

Force = mass x acceleration Newton’s second law 1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). acceleration = _force_ mass So acceleration = _1__ x force mass independent controlled (constant) If we plot the measured values of force and acceleration, what sort of graph should we get? acceleration force Answer on next slide.

Force = mass x acceleration Newton’s second law 1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). acceleration = _force_ mass So acceleration = _1__ x force mass independent controlled (constant) If we plot the measured values of force and acceleration, what sort of graph should we get? If Newton’s second law is correct, the red box above tells us that we should get a straight line through the acceleration origin, showing that the acceleration is directly proportional to the force (ie. if force is doubled, acceleration is doubled). Also, the gradient of the graph should be: (1/mass). force

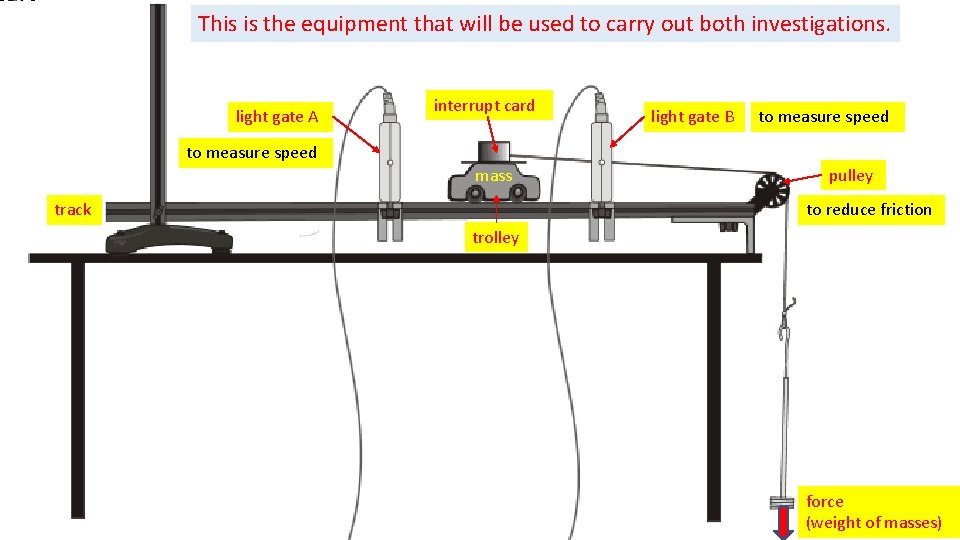
This is the equipment that will be used to carry out both investigations. light gate A interrupt card light gate B to measure speed mass track pulley to reduce friction trolley force (weight of masses)

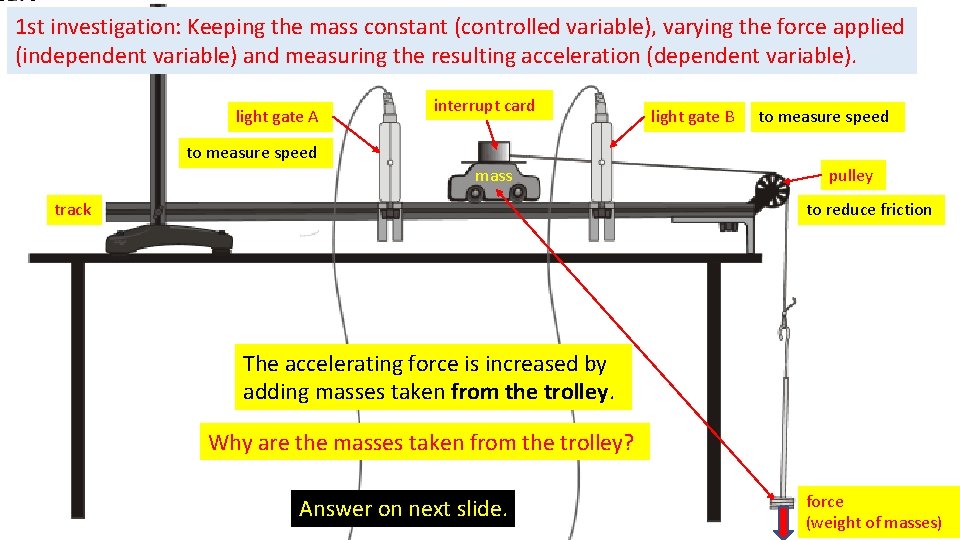
1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). light gate A interrupt card light gate B to measure speed mass track pulley to reduce friction The accelerating force is increased by adding masses taken from the trolley. Why are the masses taken from the trolley? Answer on next slide. force (weight of masses)

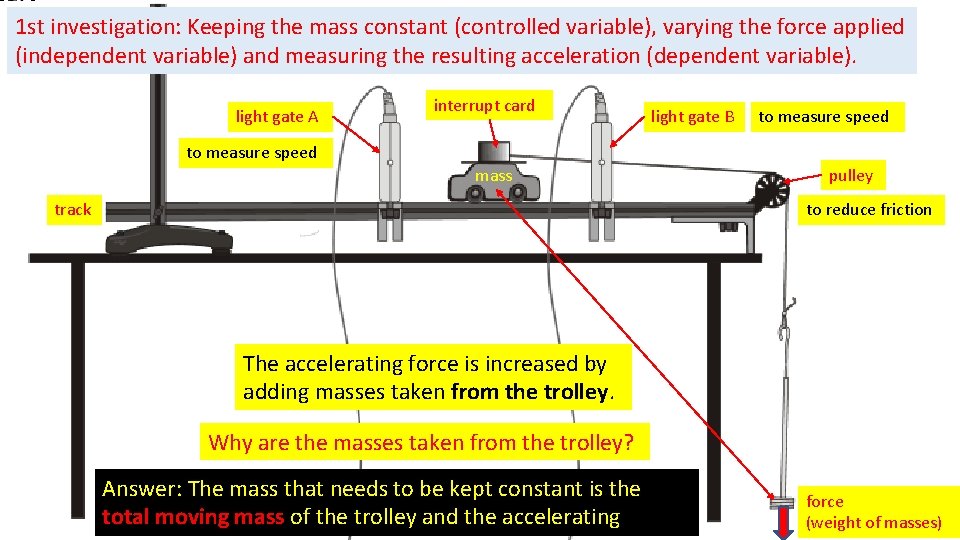
1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). light gate A interrupt card light gate B to measure speed mass track pulley to reduce friction The accelerating force is increased by adding masses taken from the trolley. Why are the masses taken from the trolley? Answer: The mass that needs to be kept constant is the total moving mass of the trolley and the accelerating force (weight of masses)

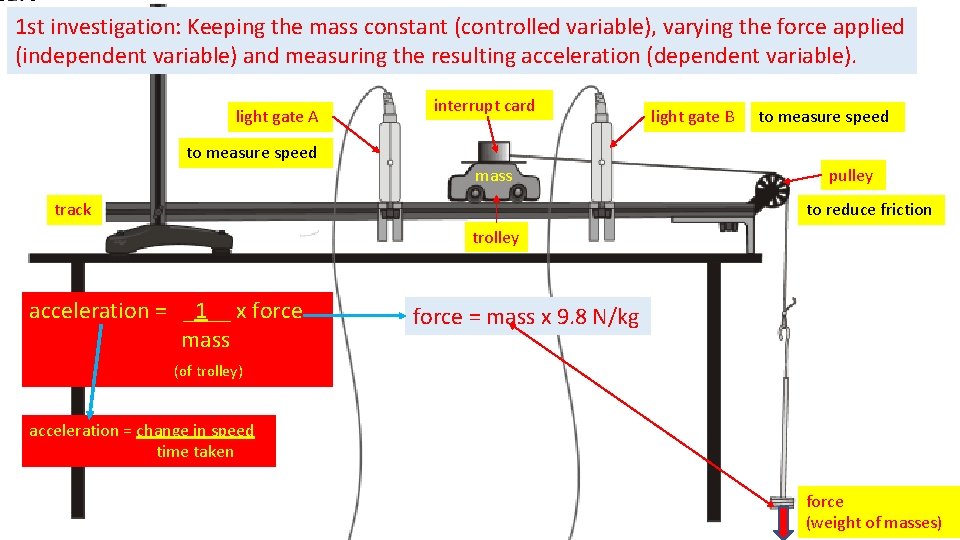
1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). light gate A interrupt card light gate B to measure speed mass track pulley to reduce friction trolley acceleration = _1__ x force mass force = mass x 9. 8 N/kg (of trolley) acceleration = change in speed time taken force (weight of masses)

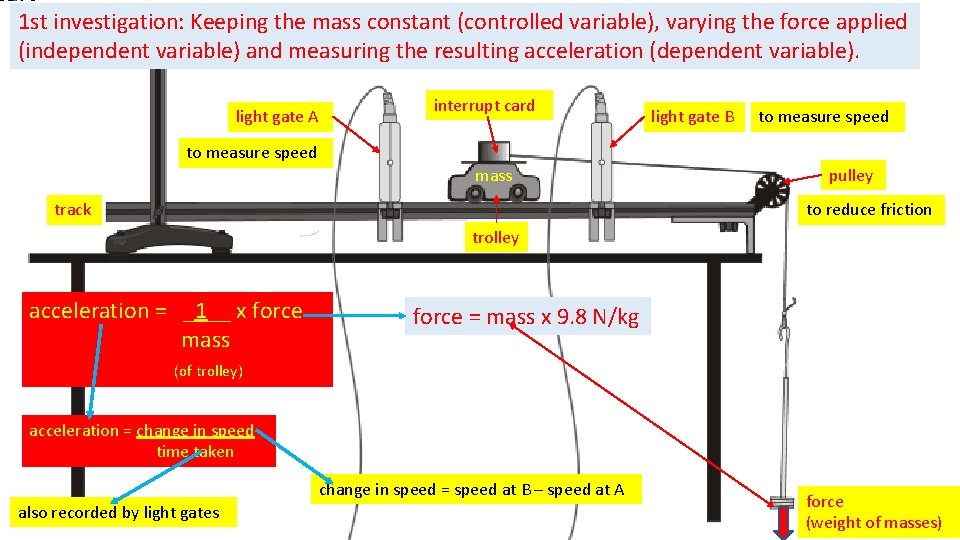
1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). light gate A interrupt card light gate B to measure speed mass track pulley to reduce friction trolley acceleration = _1__ x force mass force = mass x 9. 8 N/kg (of trolley) acceleration = change in speed time taken change in speed = speed at B – speed at A also recorded by light gates force (weight of masses)

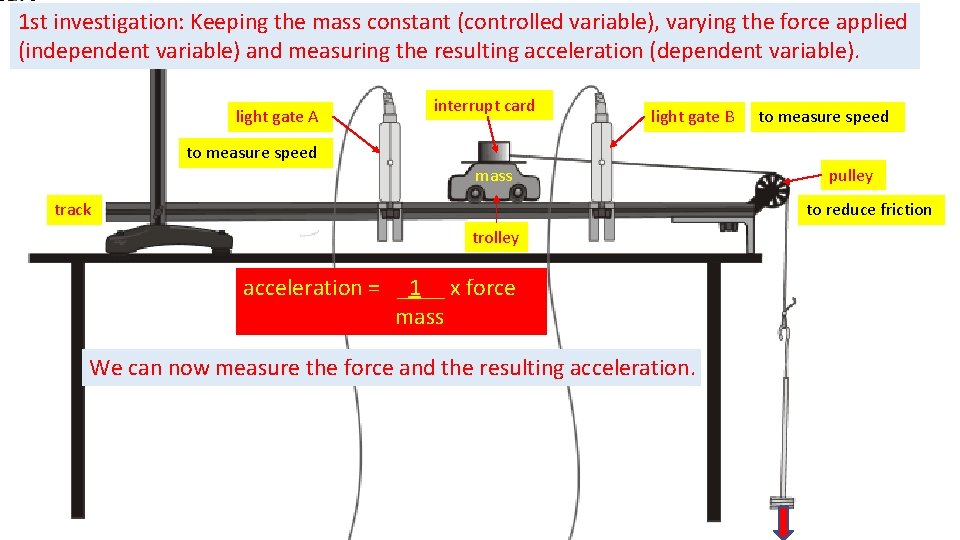
1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). light gate A interrupt card light gate B to measure speed mass track pulley to reduce friction trolley acceleration = _1__ x force mass We can now measure the force and the resulting acceleration.

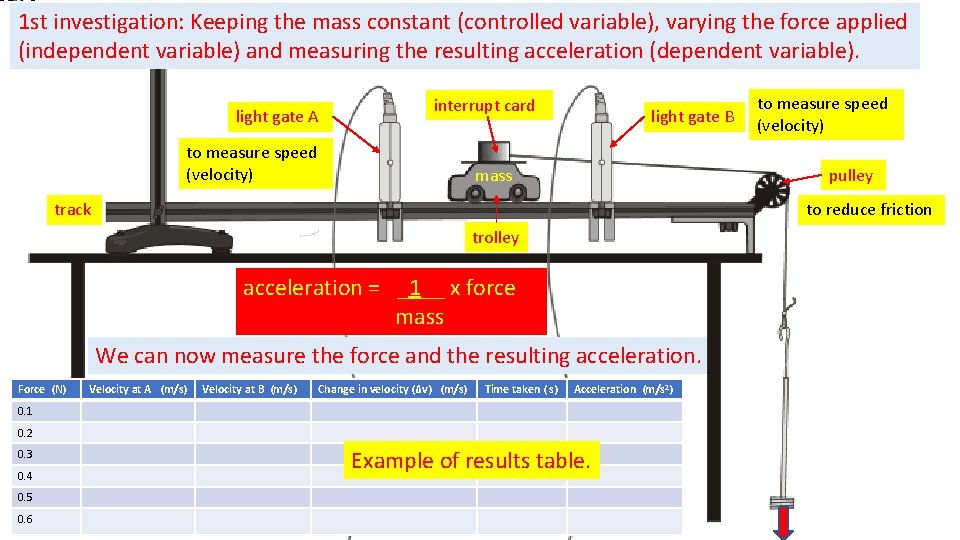
1 st investigation: Keeping the mass constant (controlled variable), varying the force applied (independent variable) and measuring the resulting acceleration (dependent variable). light gate A interrupt card to measure speed (velocity) light gate B pulley mass track to reduce friction trolley acceleration = _1__ x force mass We can now measure the force and the resulting acceleration. Force (N) Velocity at A (m/s) Velocity at B (m/s) Change in velocity (Δv) (m/s) Time taken ( s) Acceleration (m/s 2) 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 to measure speed (velocity) Example of results table.

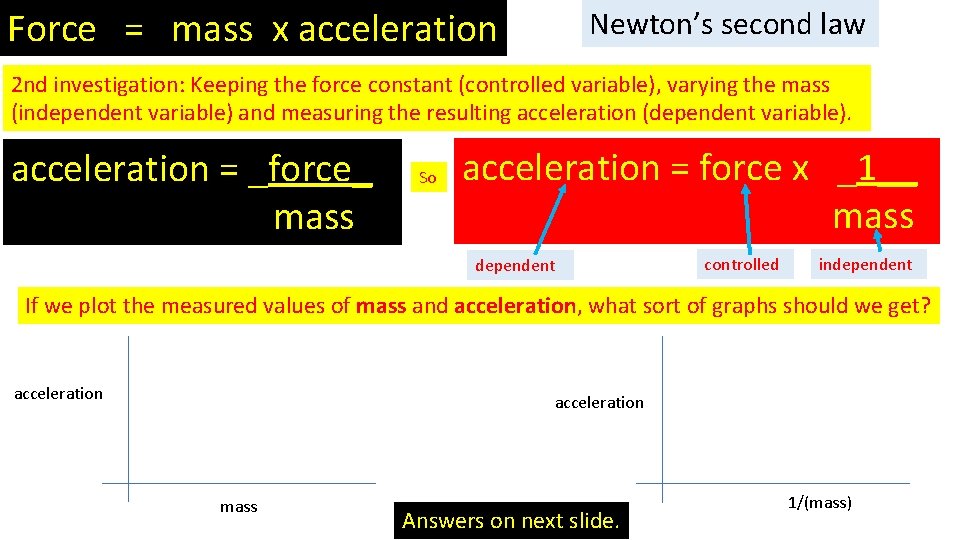
Force = mass x acceleration Newton’s second law 2 nd investigation: Keeping the force constant (controlled variable), varying the mass (independent variable) and measuring the resulting acceleration (dependent variable). acceleration = _force_ mass So acceleration = force x _1__ mass dependent controlled independent If we plot the measured values of mass and acceleration, what sort of graphs should we get? acceleration mass Answers on next slide. 1/(mass)

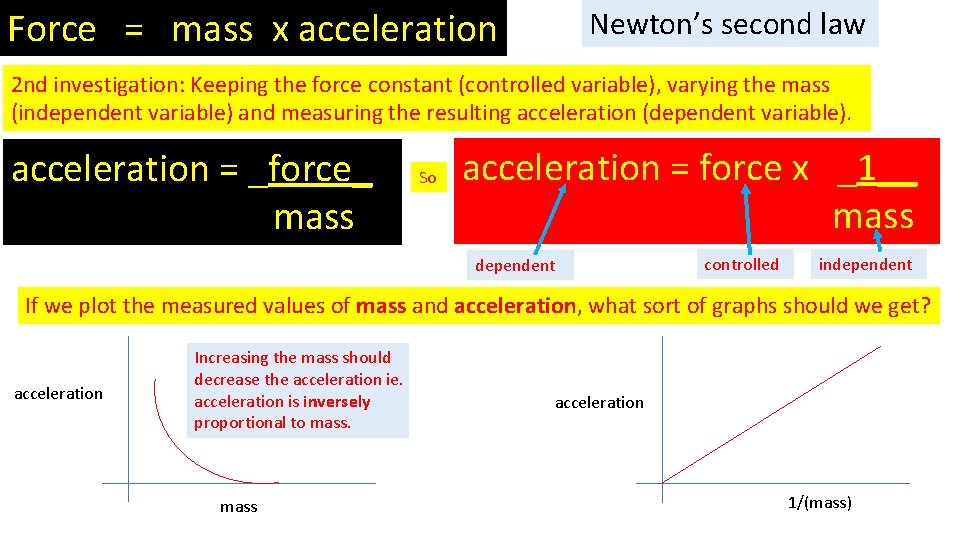
Force = mass x acceleration Newton’s second law 2 nd investigation: Keeping the force constant (controlled variable), varying the mass (independent variable) and measuring the resulting acceleration (dependent variable). acceleration = _force_ mass So acceleration = force x _1__ mass dependent controlled independent If we plot the measured values of mass and acceleration, what sort of graphs should we get? acceleration Increasing the mass should decrease the acceleration ie. acceleration is inversely proportional to mass acceleration 1/(mass)

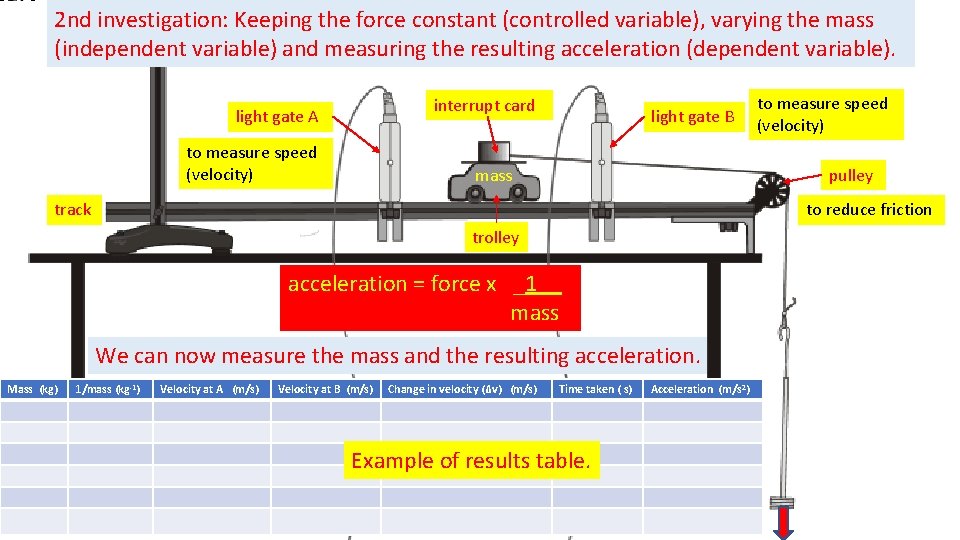
2 nd investigation: Keeping the force constant (controlled variable), varying the mass (independent variable) and measuring the resulting acceleration (dependent variable). interrupt card light gate A to measure speed (velocity) light gate B pulley mass track to reduce friction trolley acceleration = force x _1__ mass We can now measure the mass and the resulting acceleration. Mass (kg) to measure speed (velocity) 1/mass (kg-1) Velocity at A (m/s) Velocity at B (m/s) Change in velocity (Δv) (m/s) Time taken ( s) Example of results table. Acceleration (m/s 2)

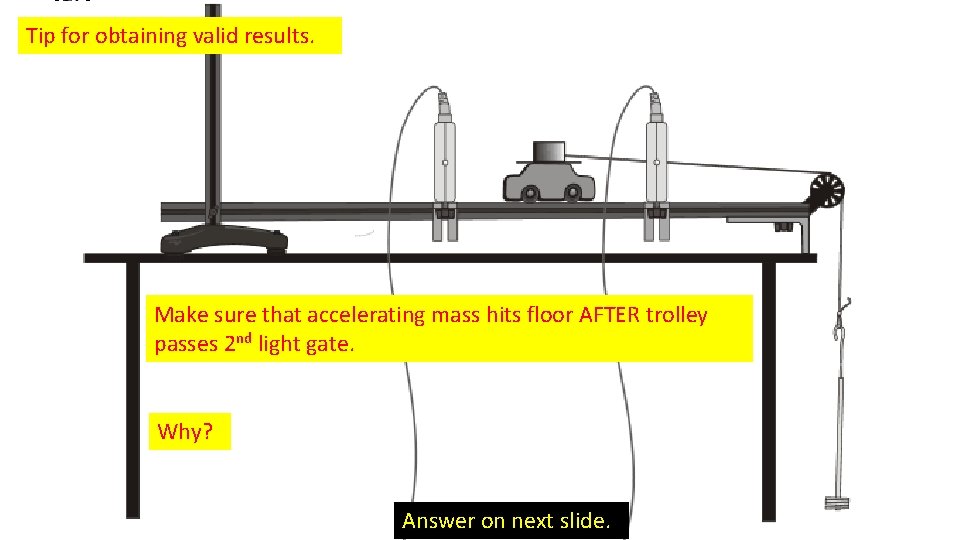
Tip for obtaining valid results. Make sure that accelerating mass hits floor AFTER trolley passes 2 nd light gate. Why? Answer on next slide.

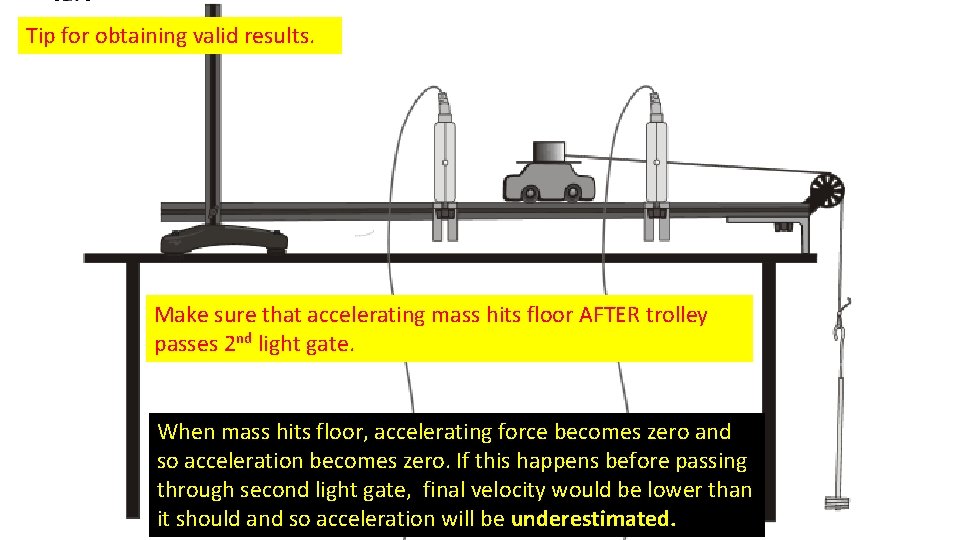
Tip for obtaining valid results. Make sure that accelerating mass hits floor AFTER trolley passes 2 nd light gate. When mass hits floor, accelerating force becomes zero and so acceleration becomes zero. If this happens before passing through second light gate, final velocity would be lower than it should and so acceleration will be underestimated.