Physics Beyond 2000 Chapter 5 Simple Harmonic Motion

Physics Beyond 2000 Chapter 5 Simple Harmonic Motion http: //library. thinkquest. org/28388/Mechanics/Moti ons/SHM. htm

Simple Harmonic Motion • It is a particular kind of oscillation. • Abbreviation is SHM. • Some terms Amplitude, period, frequency and angular frequency. http: //www. physics. uoguelph. ca/tutorials/shm/Q. shm. html

Definition of SHM • The motion of the particle whose acceleration a is always directed towards a fixed point and is directly proportional to the distance x of the particle form that point. where ωis a constant, the angular frequency.

Examples of SHM The particle is at the position x = 0. It has a velocity to the right. V 0 x=0

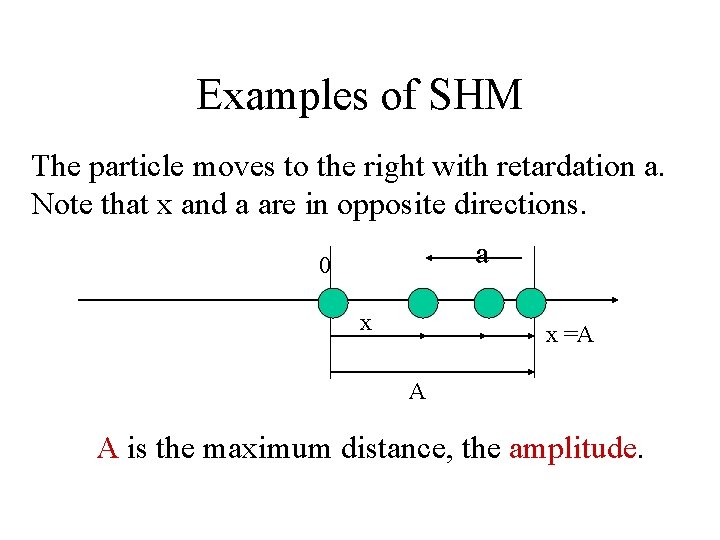
Examples of SHM The particle moves to the right with retardation a. Note that x and a are in opposite directions. a 0 x x =A A A is the maximum distance, the amplitude.

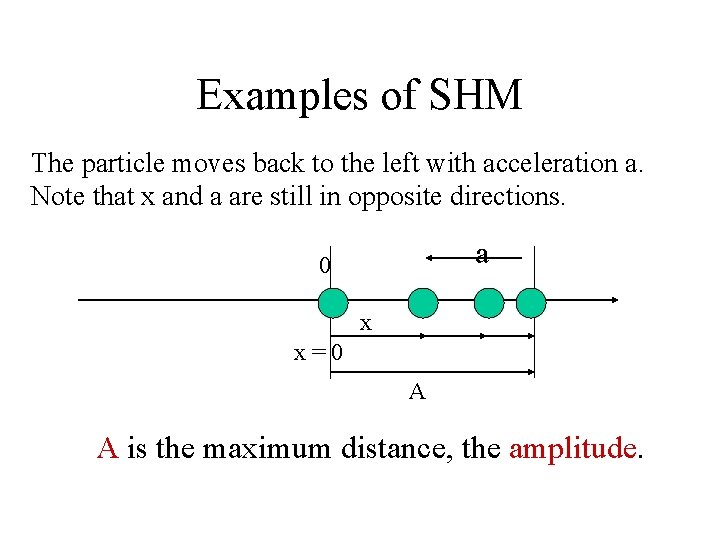
Examples of SHM The particle moves back to the left with acceleration a. Note that x and a are still in opposite directions. a 0 x x=0 A A is the maximum distance, the amplitude.

Examples of SHM The particle moves to the left with retardation a. Note that both x and a change directions. They are still in opposite directions. a 0 x x = -A A A is the maximum distance, the amplitude.

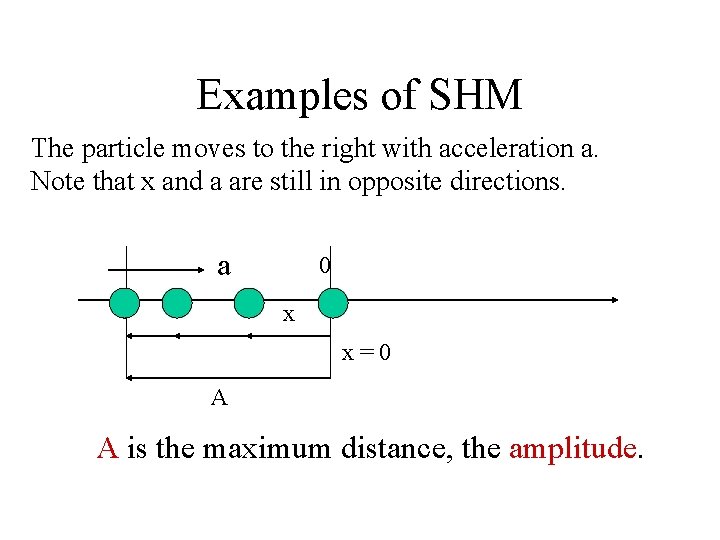
Examples of SHM The particle moves to the right with acceleration a. Note that x and a are still in opposite directions. a 0 x x=0 A A is the maximum distance, the amplitude.

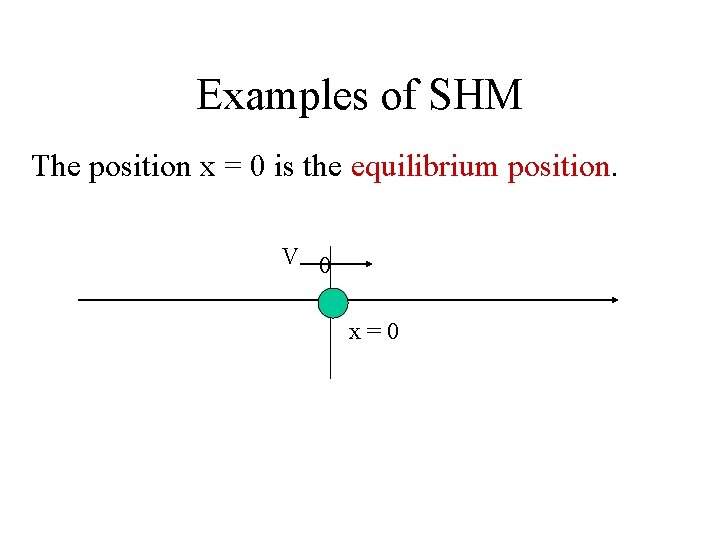
Examples of SHM The position x = 0 is the equilibrium position. V 0 x=0

Examples of SHM The position x = 0 is the equilibrium position at which the net force is zero. a 0 In the oscillation, x V The negative sign indicates the direction of a is opposite to that of x.

Example 1 • Is it a SHM? • a = -16. x

Differential equation of SHM • acceleration a of SHM The left hand sides show the accelerations in different mathematical forms.

The kinematics of SHM • Displacement x of a SHM. • A solution of the differential equation is x = A. sin(ωt + ψ) t is the time, ωis the angular frequency, A is the amplitude and ψis the initial phase.

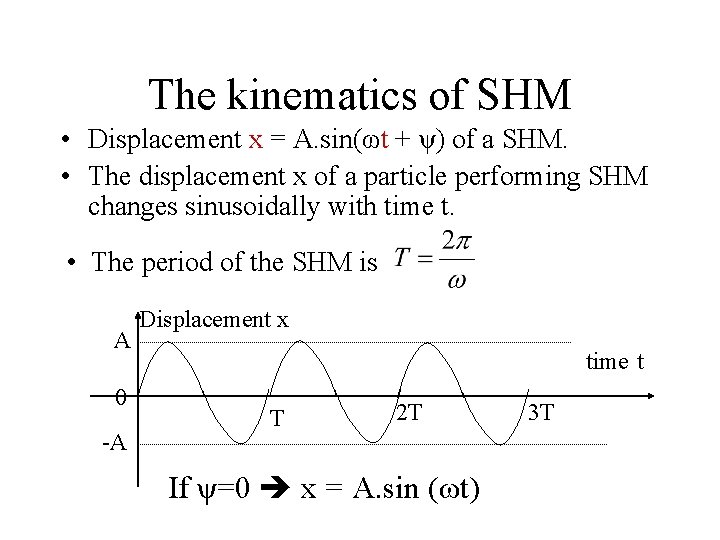
The kinematics of SHM • Displacement x = A. sin(ωt + ψ) of a SHM. • The displacement x of a particle performing SHM changes sinusoidally with time t. • The period of the SHM is A 0 -A Displacement x time t T 2 T If ψ=0 x = A. sin (ωt) 3 T

Phase and Initial Phase • x = A. sin(ωt + ψ) ωt + ψis called the phase. • At t = 0, phase reduces to ψ. x = A. sin(ψ) ψis called the initial phase.

Initial Phase ψ The value of ψis determined by the initial position of x (at t = 0). i. e. how the motion is started.

ψ= 0 • x = A. sin(ωt) • At t = 0, x = 0. – The motion starts at x = 0. • In the first T/4, x increases with time t and approaches the amplitude A. V a 0 At t = 0 x=0

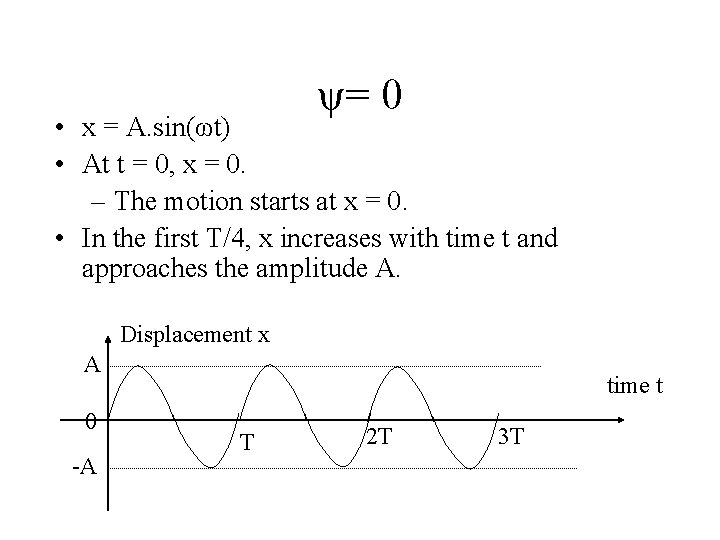
ψ= 0 • x = A. sin(ωt) • At t = 0, x = 0. – The motion starts at x = 0. • In the first T/4, x increases with time t and approaches the amplitude A. Displacement x A 0 -A time t T 2 T 3 T

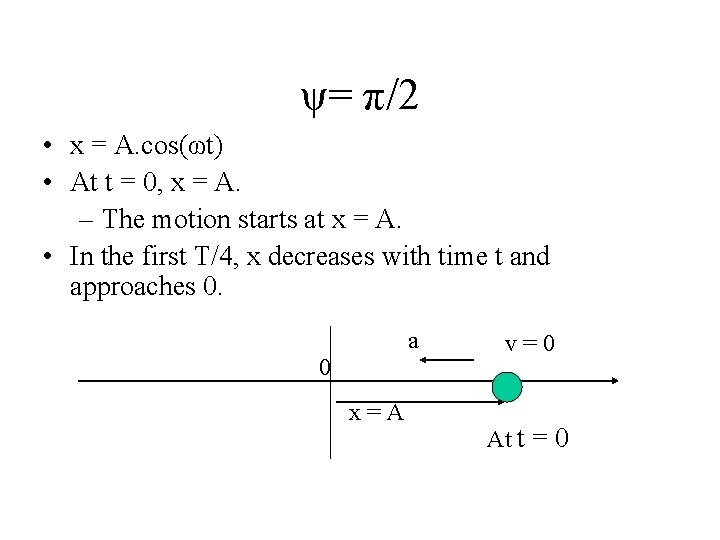
ψ= π/2 • x = A. cos(ωt) • At t = 0, x = A. – The motion starts at x = A. • In the first T/4, x decreases with time t and approaches 0. a 0 x=A v=0 At t = 0

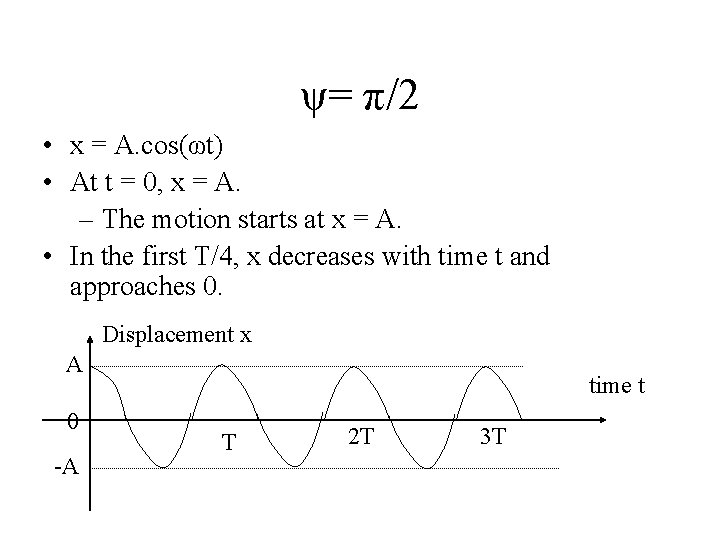
ψ= π/2 • x = A. cos(ωt) • At t = 0, x = A. – The motion starts at x = A. • In the first T/4, x decreases with time t and approaches 0. Displacement x A 0 -A time t T 2 T 3 T

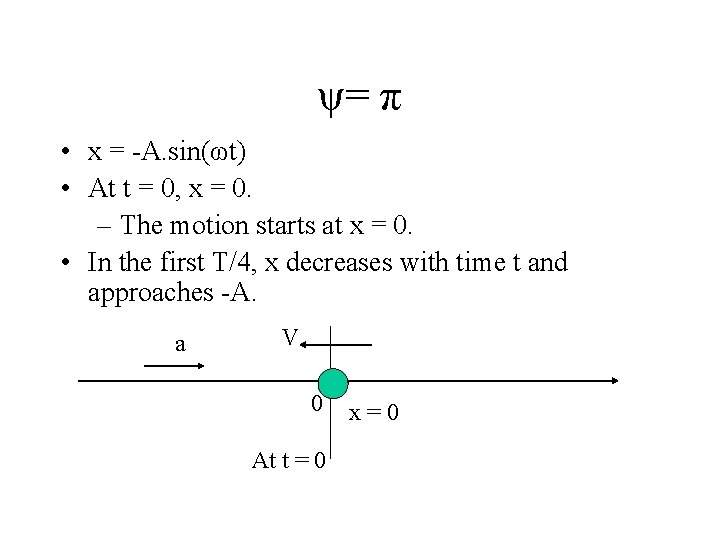
ψ= π • x = -A. sin(ωt) • At t = 0, x = 0. – The motion starts at x = 0. • In the first T/4, x decreases with time t and approaches -A. a V 0 At t = 0 x=0

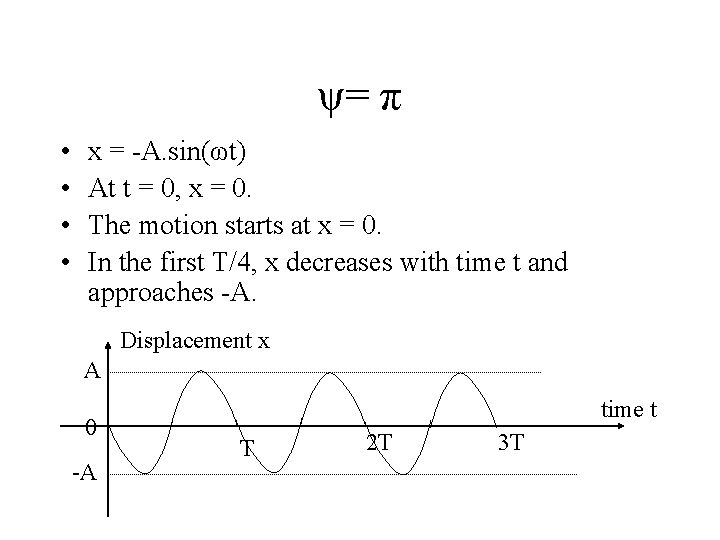
ψ= π • • x = -A. sin(ωt) At t = 0, x = 0. The motion starts at x = 0. In the first T/4, x decreases with time t and approaches -A. Displacement x A 0 -A time t T 2 T 3 T

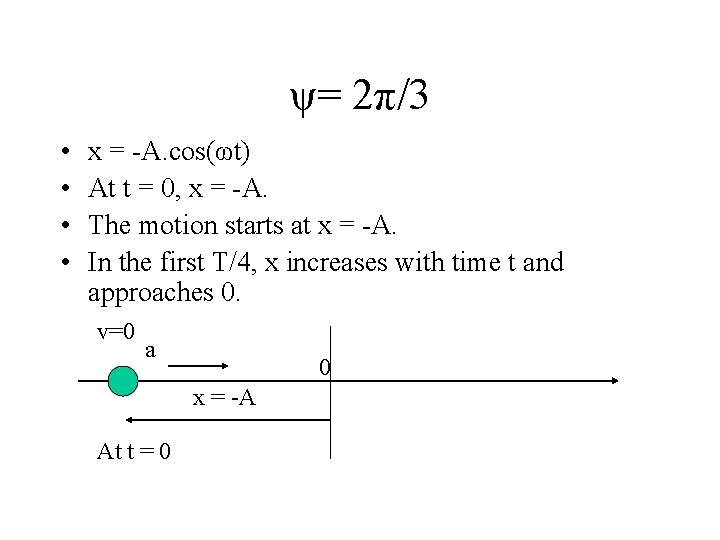
ψ= 2π/3 • • x = -A. cos(ωt) At t = 0, x = -A. The motion starts at x = -A. In the first T/4, x increases with time t and approaches 0. v=0 a 0 x = -A At t = 0

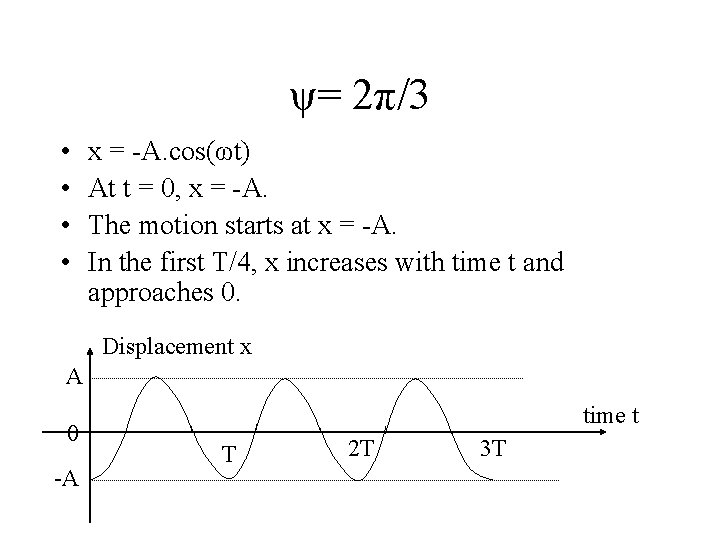
ψ= 2π/3 • • x = -A. cos(ωt) At t = 0, x = -A. The motion starts at x = -A. In the first T/4, x increases with time t and approaches 0. Displacement x A 0 -A time t T 2 T 3 T

Angular frequency ω • Period T = time for one complete oscillation. • Frequency f = number of oscillations in one second. • Angular frequency = 2 f

Angular frequency ω • In a SHM, x = A. sin(ωt+ψ) • After a time T, x must be the same again. • A. sin(ωt+ψ) = A. sin(ωt+ ωT +ψ) ωT = 2π Unit of ω is rad s-1

Isochronous oscillation • The period T in a SHM is independent of the amplitude A. • A SHM is an isochronous oscillation.

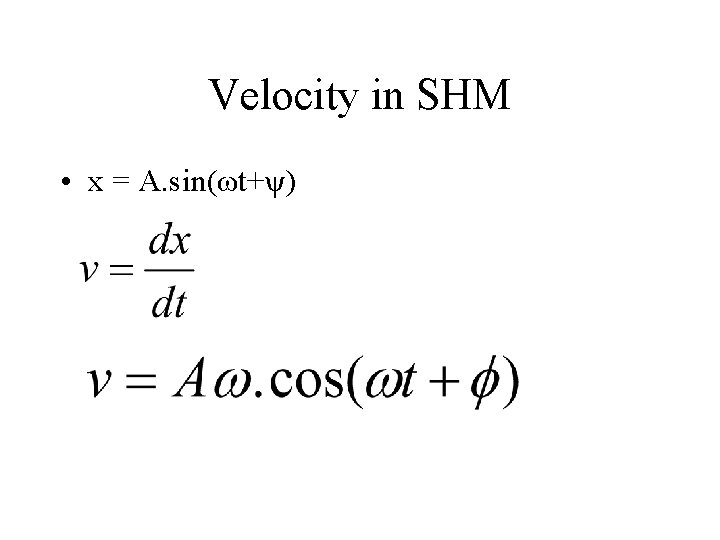
Velocity in SHM • x = A. sin(ωt+ψ)

Velocity in SHM • x = A. sin(ωt+ψ) What is the maximum speed in this motion? vo = Aω The maximum speed occurs at the equilibrium position. i. e. when x = 0.

Velocity in SHM • Example 2.

Acceleration in SHM

Acceleration in SHM What is the maximum acceleration in this motion? ao = -Aω2 or Aω2 The maximum acceleration occurs at the positions with maximum displacement. i. e. when x = A or -A.

Displacement, Velocity and Acceleration in SHM x = A. sin(ωt + ψ) • v = Aω. cos(ωt + ψ) • a = -Aω2. sin(ωt + ψ) •

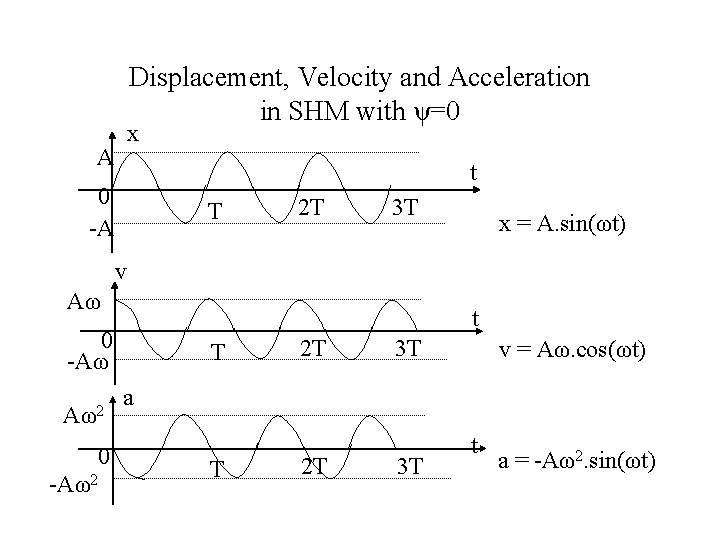
Displacement, Velocity and Acceleration in SHM with ψ=0 x A t 0 -A T 2 T 3 T x = A. sin(ωt) v Aω t 0 -Aω Aω2 0 -Aω2 T 2 T 3 T v = Aω. cos(ωt) a T 2 T 3 T t a = -Aω2. sin(ωt)

Acceleration and Displacement in SHM • x = A. sin(ωt + ψ) • a = -Aω2. sin(ωt + ψ) 2 • a = - ω. x • This is a characteristic of a SHM.

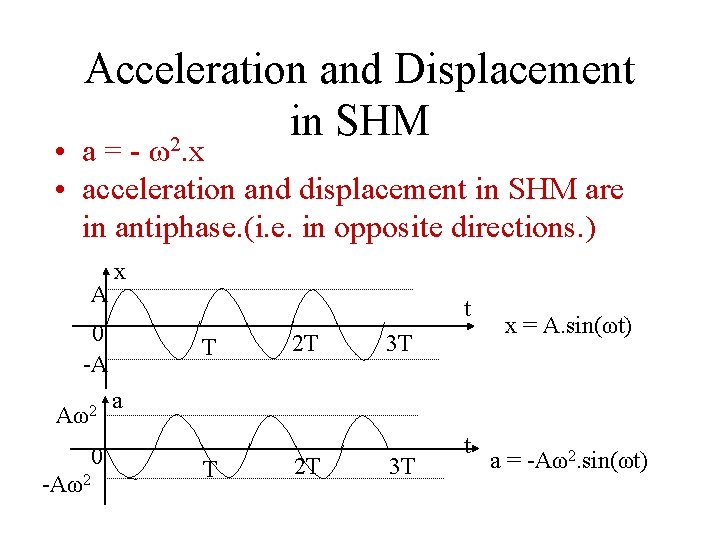
Acceleration and Displacement in SHM 2 • a = - ω. x • acceleration and displacement in SHM are in antiphase. (i. e. in opposite directions. ) A x t 0 -A Aω2 0 -Aω2 T 2 T 3 T x = A. sin(ωt) a T 2 T 3 T t a = -Aω2. sin(ωt)

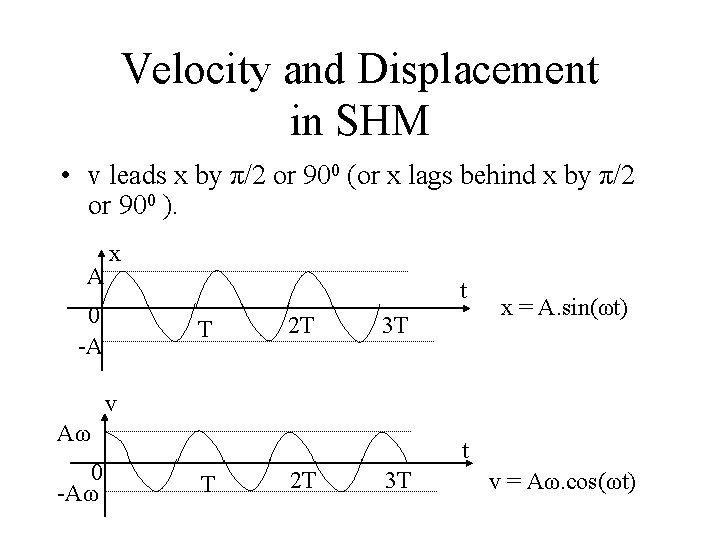
Velocity and Displacement in SHM • v leads x by π/2 or 900 (or x lags behind x by π/2 or 900 ). A x t 0 -A T 2 T 3 T x = A. sin(ωt) v Aω 0 -Aω t T 2 T 3 T v = Aω. cos(ωt)

Velocity and Displacement in SHM • v leads x by π/2 or 900. •

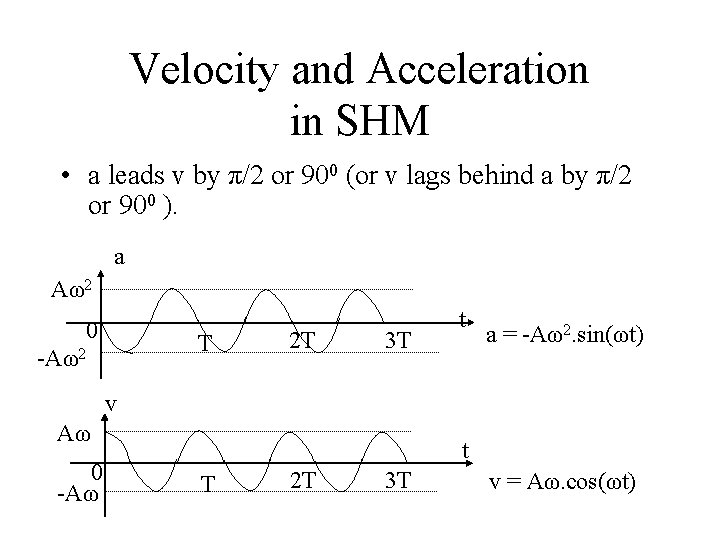
Velocity and Acceleration in SHM • a leads v by π/2 or 900 (or v lags behind a by π/2 or 900 ). a Aω2 0 T -Aω2 2 T 3 T t a = -Aω2. sin(ωt) v Aω 0 -Aω t T 2 T 3 T v = Aω. cos(ωt)

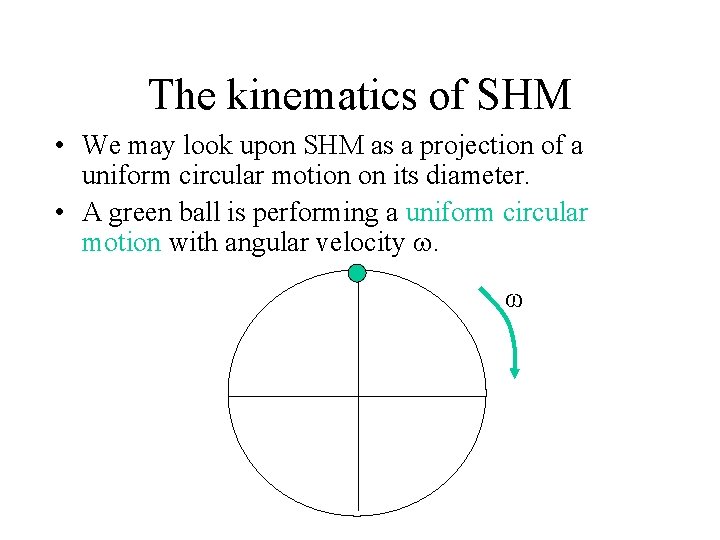
The kinematics of SHM • We may look upon SHM as a projection of a uniform circular motion on its diameter. • A green ball is performing a uniform circular motion with angular velocity . ω

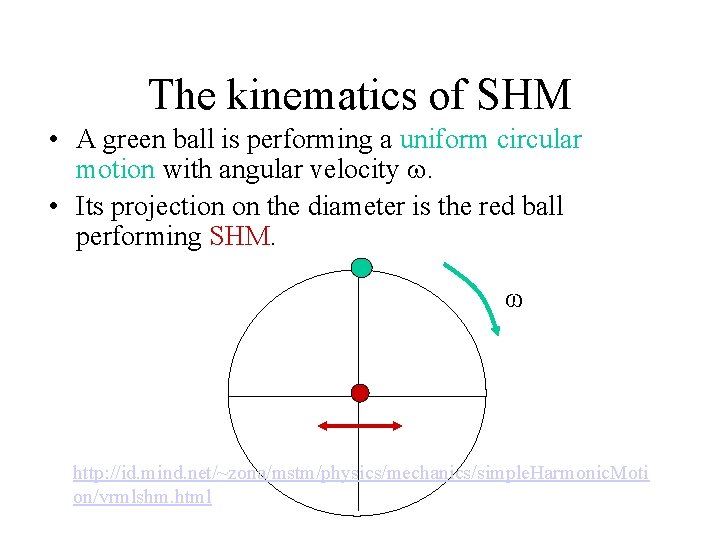
The kinematics of SHM • A green ball is performing a uniform circular motion with angular velocity . • Its projection on the diameter is the red ball performing SHM. ω http: //id. mind. net/~zona/mstm/physics/mechanics/simple. Harmonic. Moti on/vrmlshm. html

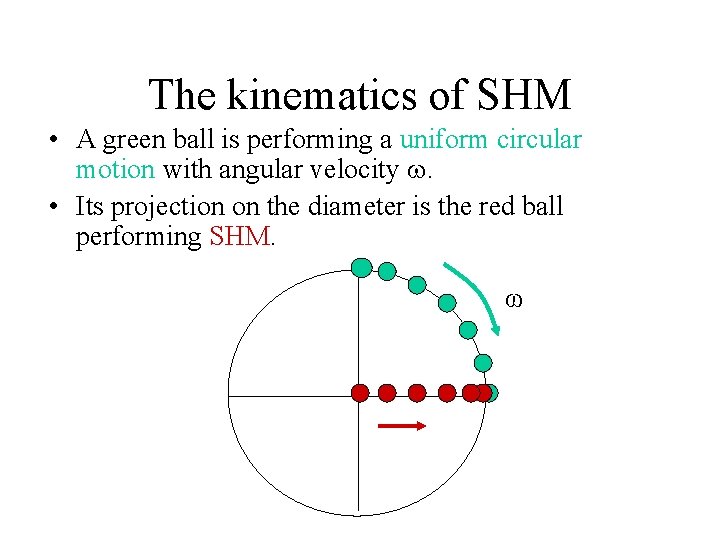
The kinematics of SHM • A green ball is performing a uniform circular motion with angular velocity . • Its projection on the diameter is the red ball performing SHM. ω

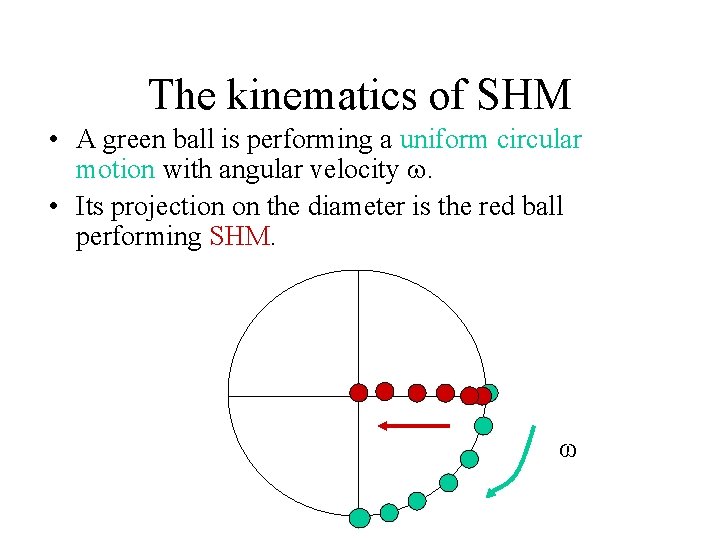
The kinematics of SHM • A green ball is performing a uniform circular motion with angular velocity . • Its projection on the diameter is the red ball performing SHM. ω

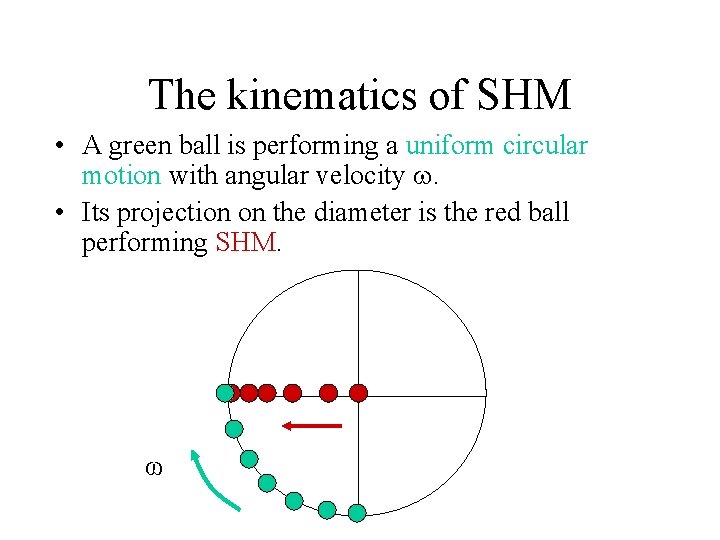
The kinematics of SHM • A green ball is performing a uniform circular motion with angular velocity . • Its projection on the diameter is the red ball performing SHM. ω

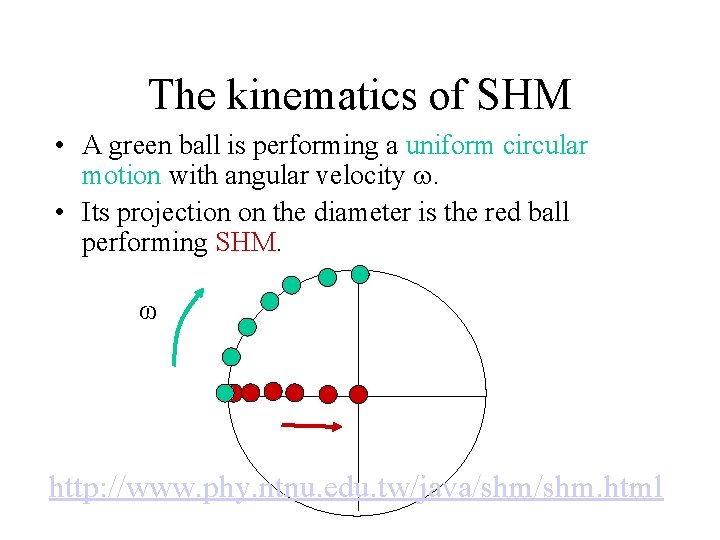
The kinematics of SHM • A green ball is performing a uniform circular motion with angular velocity . • Its projection on the diameter is the red ball performing SHM. ω http: //www. phy. ntnu. edu. tw/java/shm. html

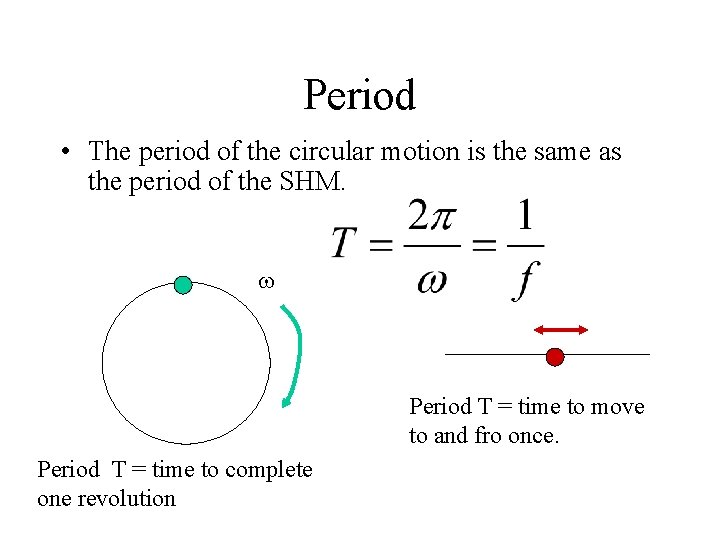
Period • The period of the circular motion is the same as the period of the SHM. Period T = time to move to and fro once. Period T = time to complete one revolution

Displacement of SHM ω O A At time = 0, the position of the green ball and the red ball are as shown. Let A = radius of the circle It is also the amplitude of the SHM Let be the starting angle of the green ball. It is the initial phase of the red ball.

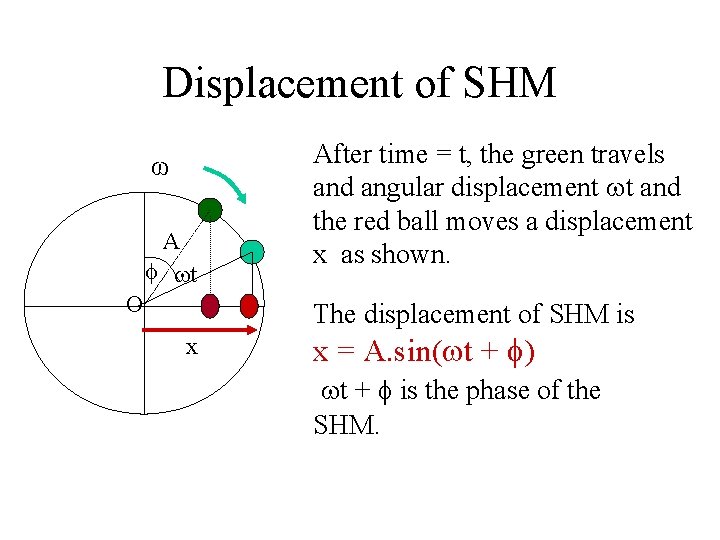
Displacement of SHM ω A t O After time = t, the green travels and angular displacement t and the red ball moves a displacement x as shown. The displacement of SHM is x x = A. sin( t + ) t + is the phase of the SHM.

Velocity of SHM ω + t A O v The linear speed of the green ball is A. The velocity of the red ball is the horizontal component of A . A v = A . cos( t + ) Let A = vo v = vo. cos( t + )

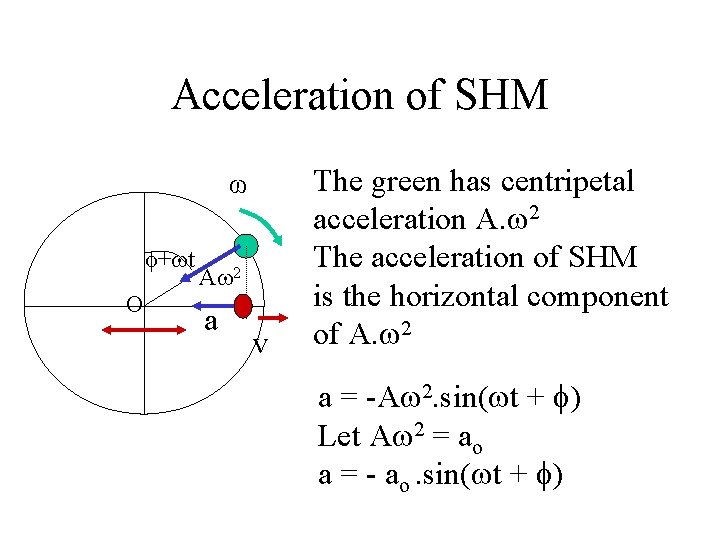
Acceleration of SHM ω + t O A 2 a v The green has centripetal acceleration A. 2 The acceleration of SHM is the horizontal component of A. 2 a = -A 2. sin( t + ) Let A 2 = ao a = - ao. sin( t + )

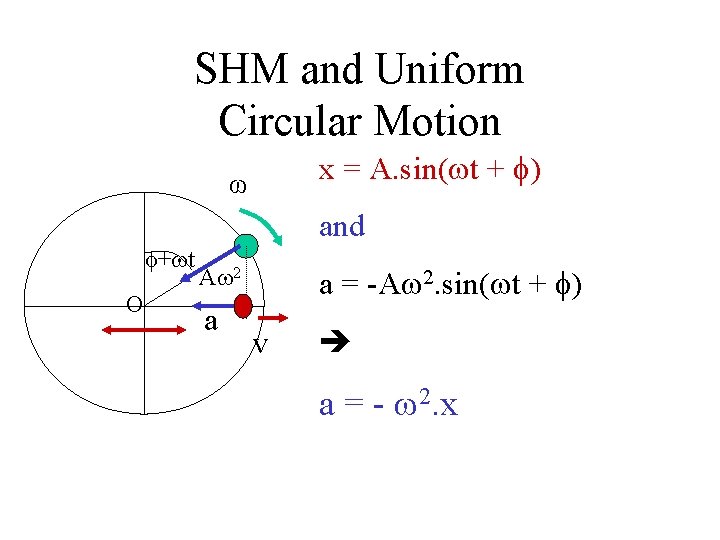
SHM and Uniform Circular Motion x = A. sin( t + ) ω + t O and a = -A 2. sin( t + ) A 2 a v a = - 2. x

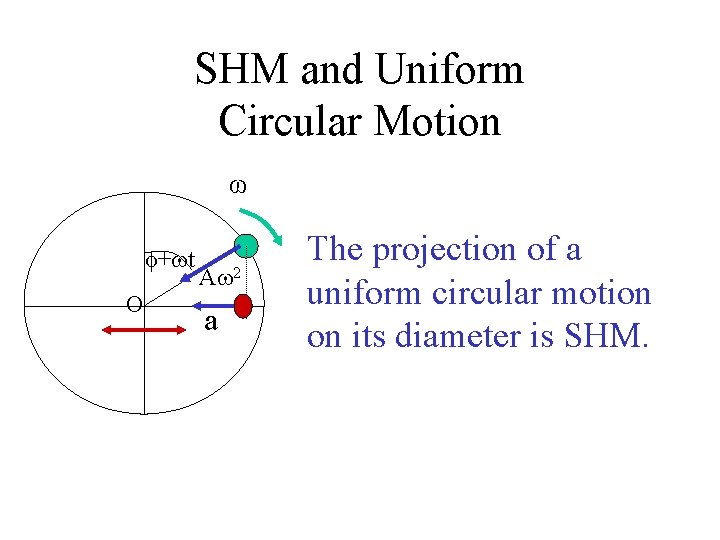
SHM and Uniform Circular Motion ω + t O A 2 a The projection of a uniform circular motion on its diameter is SHM.

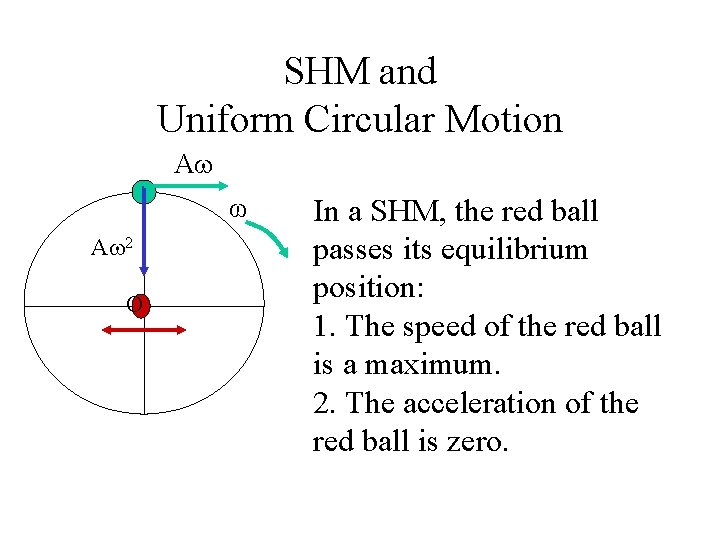
SHM and Uniform Circular Motion A ω A 2 O In a SHM, the red ball passes its equilibrium position: 1. The speed of the red ball is a maximum. 2. The acceleration of the red ball is zero.

SHM and Uniform Circular Motion ω A 2 O A In a SHM, when the red ball is at its maximum displacement: 1. The speed of the red ball is a zero. 2. The acceleration of the red ball is a maximum.

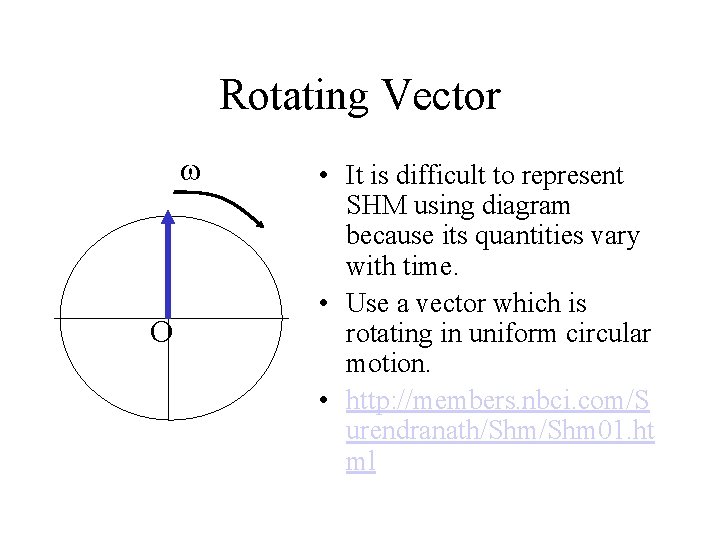
Rotating Vector O • It is difficult to represent SHM using diagram because its quantities vary with time. • Use a vector which is rotating in uniform circular motion. • http: //members. nbci. com/S urendranath/Shm 01. ht ml

Rotating Vector O • It is difficult to represent SHM using diagram because its quantities vary with time. • Use a vector which is rotating in uniform circular motion.

Rotating Vector • It is difficult to represent SHM using diagram because its quantities vary with time. • Use a vector which is rotating in uniform circular motion. O

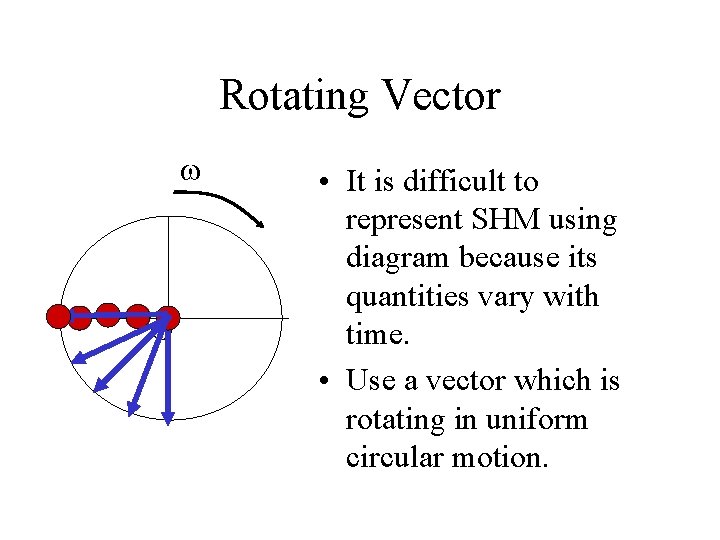
Rotating Vector • It is difficult to represent SHM using diagram because its quantities vary with time. • Use a vector which is rotating in uniform circular motion. O

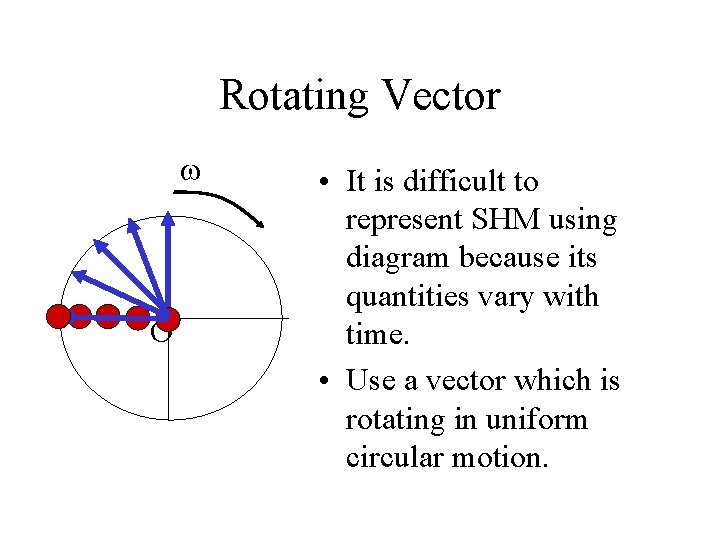
Rotating Vector O • It is difficult to represent SHM using diagram because its quantities vary with time. • Use a vector which is rotating in uniform circular motion.

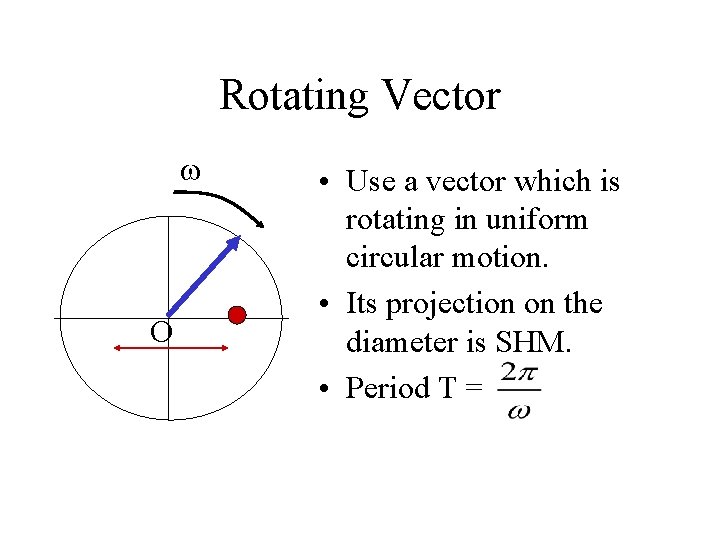
Rotating Vector O • Use a vector which is rotating in uniform circular motion. • Its projection on the diameter is SHM. • Period T =

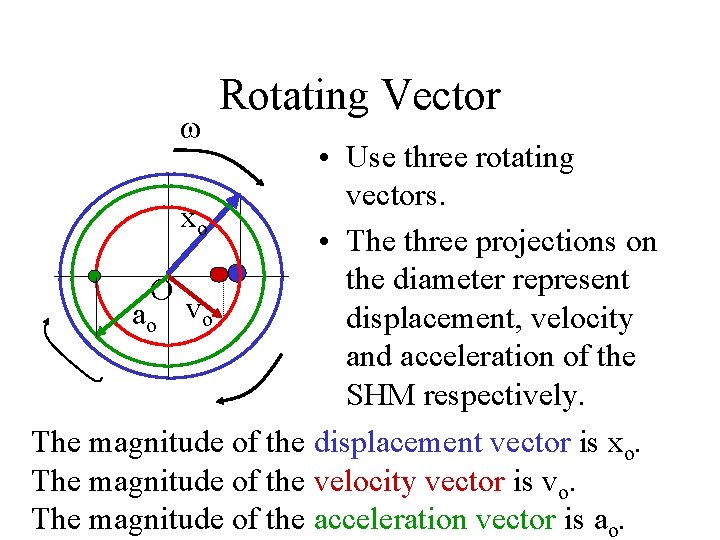
Rotating Vector • Use three rotating vectors. xo • The three projections on the diameter represent O ao vo displacement, velocity and acceleration of the SHM respectively. The magnitude of the displacement vector is xo. The magnitude of the velocity vector is vo. The magnitude of the acceleration vector is ao.

xo O ao vo Rotating Vector From the rotating vectors, the velocity v leads displacement x by π/2 and acceleration a and displacement x are in antiphase. http: //electron 6. phys. utk. edu/phys 135/ modules/m 9/oscillations. htm

x The Dynamics of SHM v a When the particle is at a displacement x, there is an acceleration a. From Newton’s 2 nd law, there must be a net force Fnet on it Fnet = m. a and in SHM a = -ω2. x The above two equations Fnet = -mω2. x

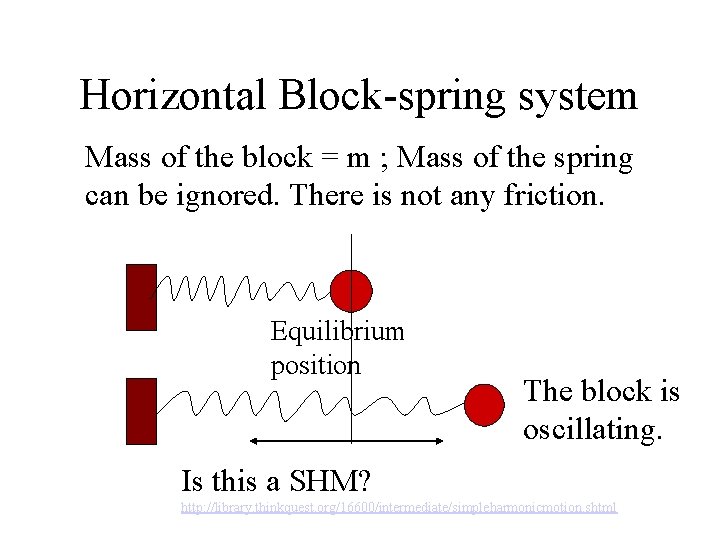
Horizontal Block-spring system Mass of the block = m ; Mass of the spring can be ignored. There is not any friction. Equilibrium position The block is oscillating. Is this a SHM? http: //library. thinkquest. org/16600/intermediate/simpleharmonicmotion. shtml

Horizontal Block-spring system Equilibrium position The block is oscillating. x Suppose that the block has been displaced by a displacement x. Fnet = m. a and Fnet = -k. x where k is the spring constant m. a = -k. x a =. x

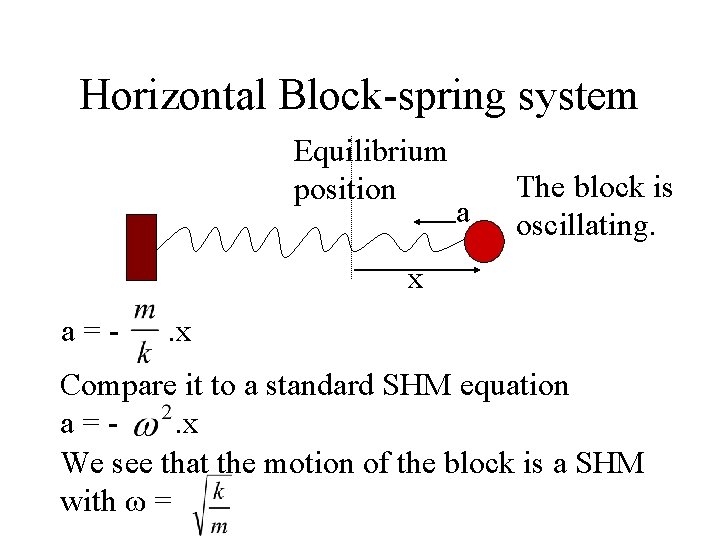
Horizontal Block-spring system Equilibrium position a The block is oscillating. x a=- . x Compare it to a standard SHM equation a=. x We see that the motion of the block is a SHM with ω =

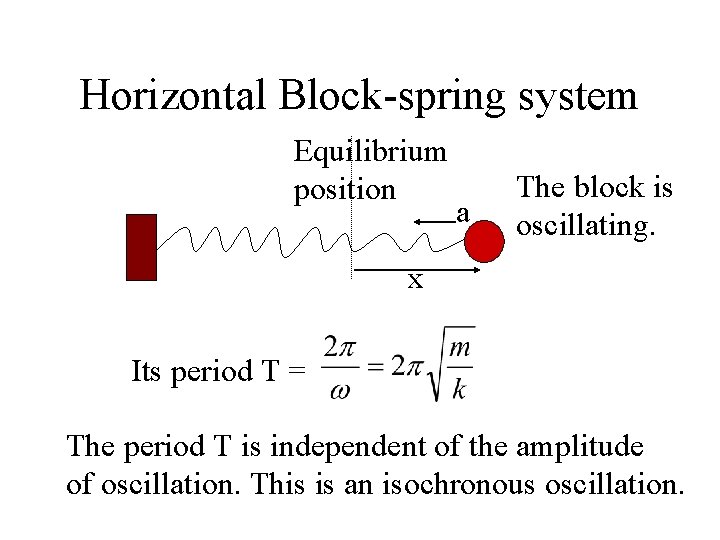
Horizontal Block-spring system Equilibrium position a The block is oscillating. x Its period T = The period T is independent of the amplitude of oscillation. This is an isochronous oscillation.

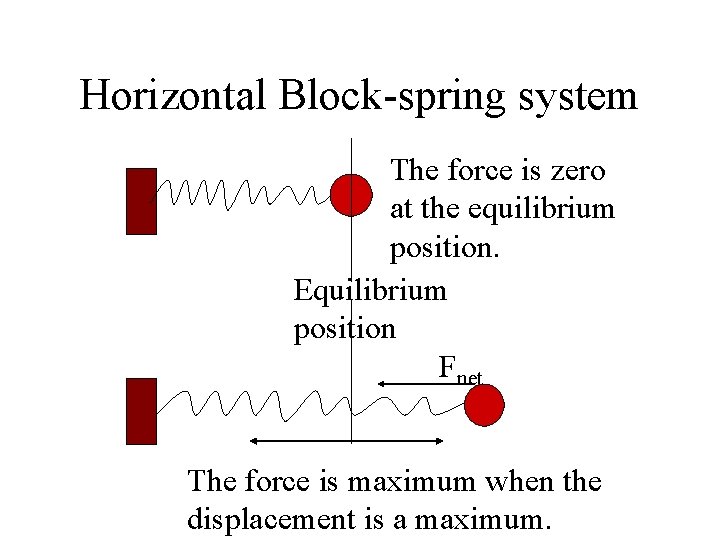
Horizontal Block-spring system The force is zero at the equilibrium position. Equilibrium position Fnet The force is maximum when the displacement is a maximum.

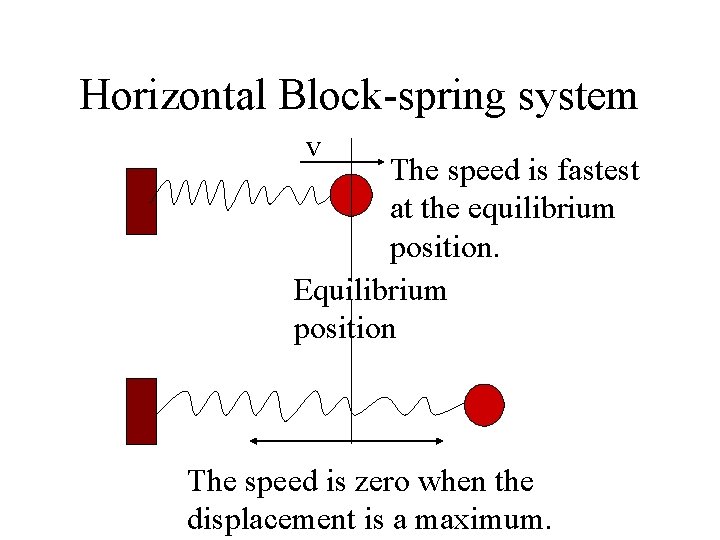
Horizontal Block-spring system v The speed is fastest at the equilibrium position. Equilibrium position The speed is zero when the displacement is a maximum.

Horizontal Block-spring system • A simulation program • You may download the program from – http: //www. programfiles. com/index. asp? ID=74 91

Vertical Block-spring system • http: //webphysics. ph. msstate. edu/javamirror /explrsci/dswmedia/harmonic. htm • http: //www. exploratorium. edu/xref/phenom ena/simple_harmonic_motion. html • http: //hyperphysics. phyastr. gsu. edu/hbase/shm. html

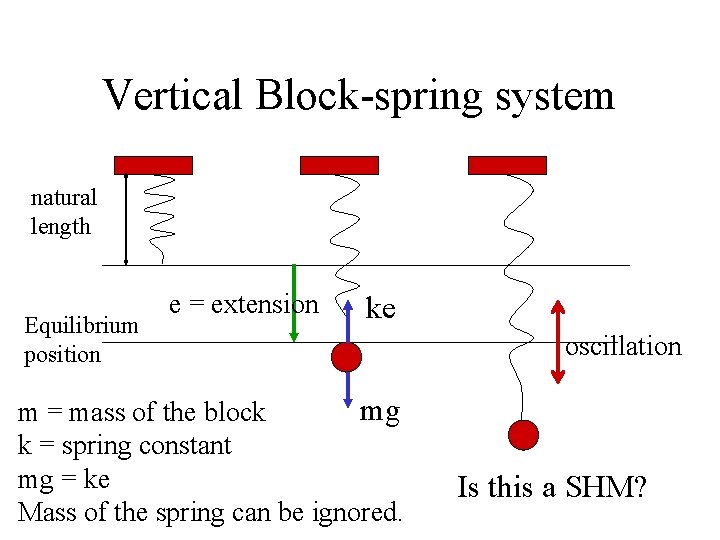
Vertical Block-spring system natural length Equilibrium position e = extension ke mg m = mass of the block k = spring constant mg = ke Mass of the spring can be ignored. oscillation Is this a SHM?

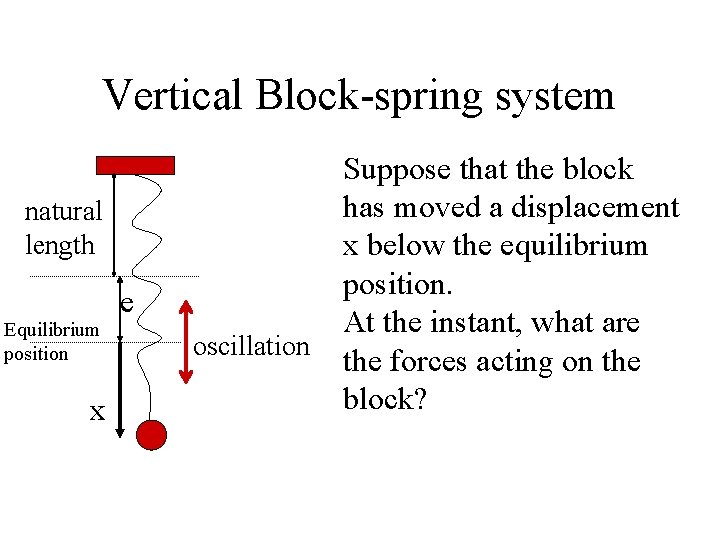
Vertical Block-spring system natural length Equilibrium position x e oscillation Suppose that the block has moved a displacement x below the equilibrium position. At the instant, what are the forces acting on the block?

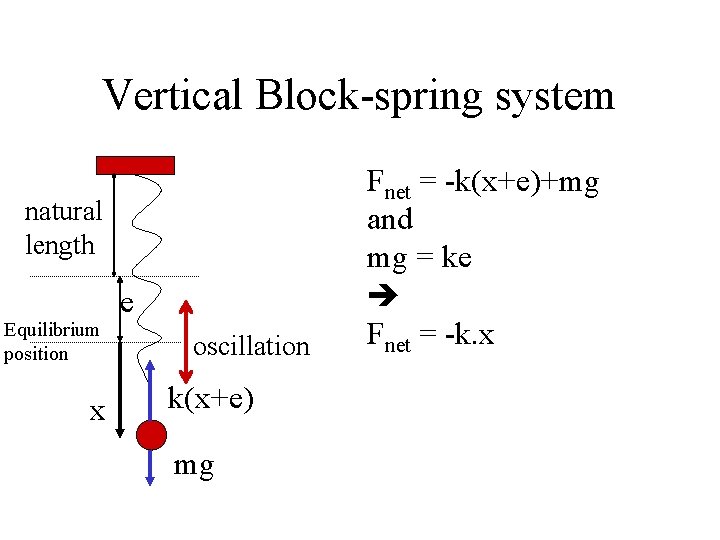
Vertical Block-spring system natural length Equilibrium position x e oscillation k(x+e) mg Fnet = -k(x+e)+mg and mg = ke Fnet = -k. x

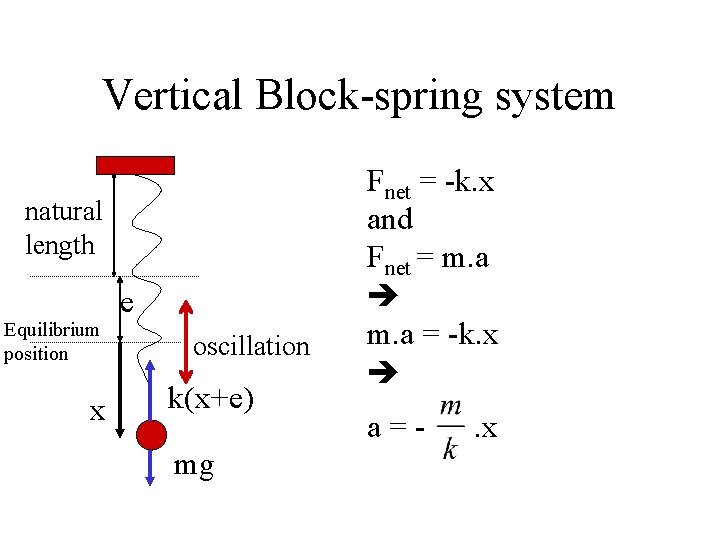
Vertical Block-spring system natural length Equilibrium position x e oscillation k(x+e) mg Fnet = -k. x and Fnet = m. a = -k. x a=- . x

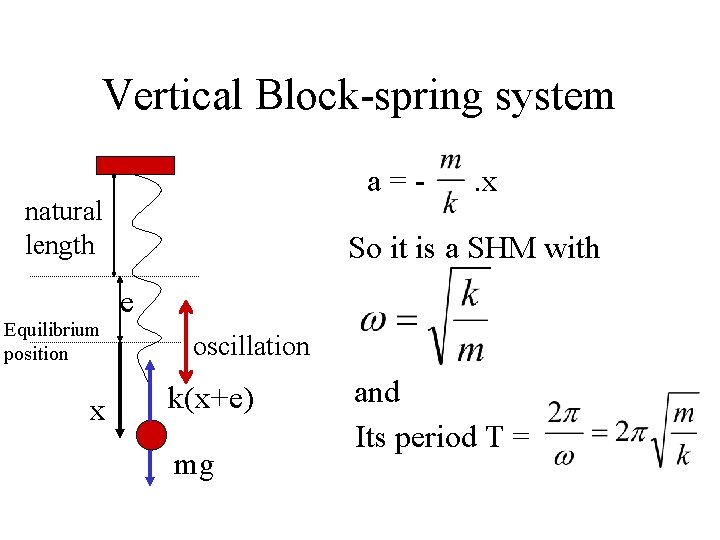
Vertical Block-spring system a=- natural length Equilibrium position x . x So it is a SHM with e oscillation k(x+e) mg and Its period T =

Vertical Block-spring system • The motion is similar to that of a horizontal block spring system. • At the equilibrium position, the net force on the block is zero though the tension of the spring is ke. • At the equilibrium position, the speed of the block is fastest. • At the maximum displacement, the net force is a maximum and the speed is zero.

Examples • Example 4 • Horizontal block-spring system. • Example 5 • Vertical block-spring system. • Example 6 • Combination of springs.

Simple pendulum The simple pendulum is set into oscillation. Is it a SHM? http: //webphysics. ph. msstate. edu/javamirro r/explrsci/dswmedia/harmonic. htm

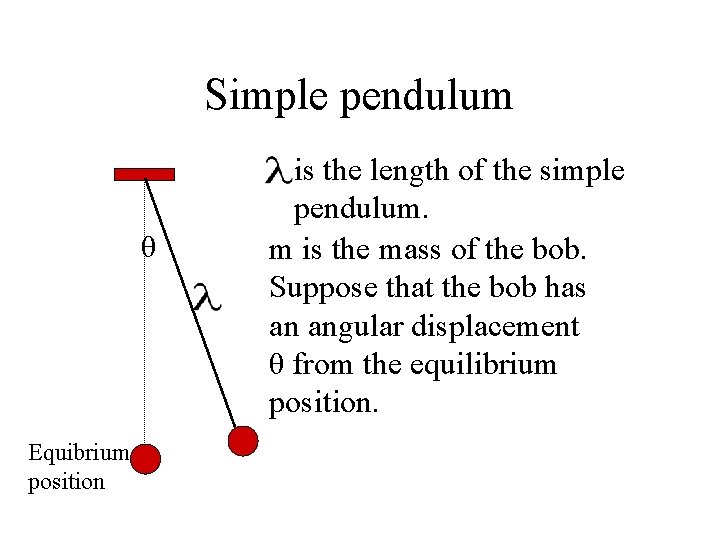
Simple pendulum θ Equibrium position is the length of the simple pendulum. m is the mass of the bob. Suppose that the bob has an angular displacement θ from the equilibrium position.

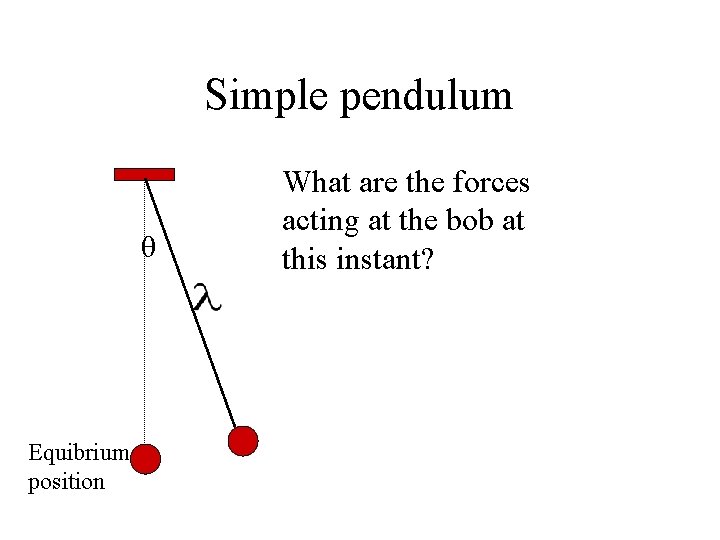
Simple pendulum θ Equibrium position What are the forces acting at the bob at this instant?

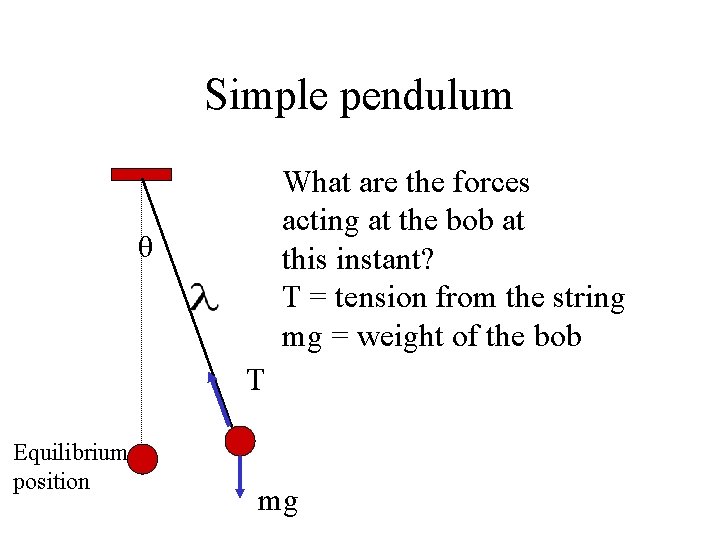
Simple pendulum What are the forces acting at the bob at this instant? T = tension from the string mg = weight of the bob θ T Equilibrium position mg

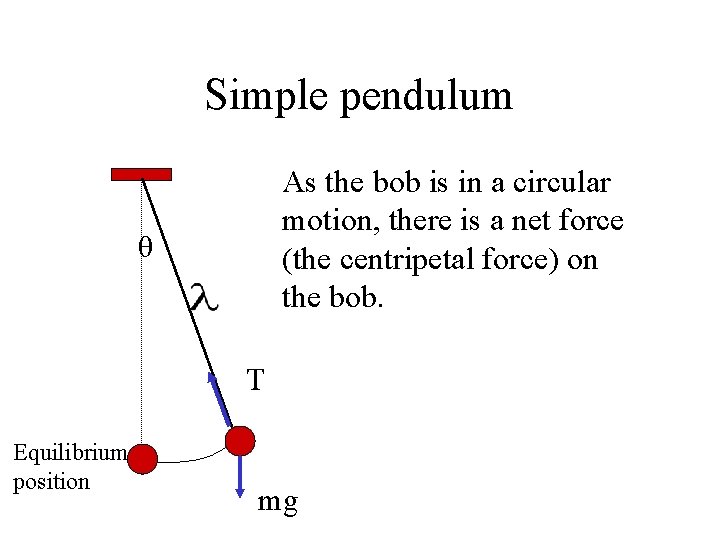
Simple pendulum As the bob is in a circular motion, there is a net force (the centripetal force) on the bob. θ T Equilibrium position mg

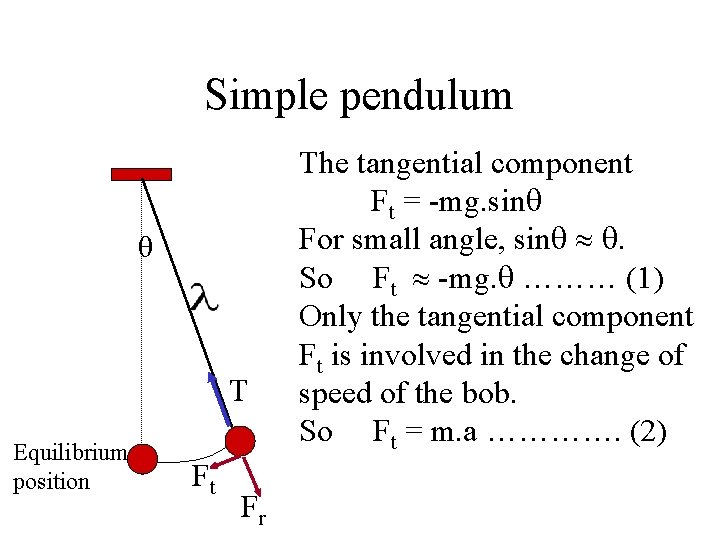
Simple pendulum θ T Equilibrium position Ft Fr The tangential component Ft = -mg. sin For small angle, sin . So Ft -mg. ……… (1) Only the tangential component Ft is involved in the change of speed of the bob. So Ft = m. a …………. (2)

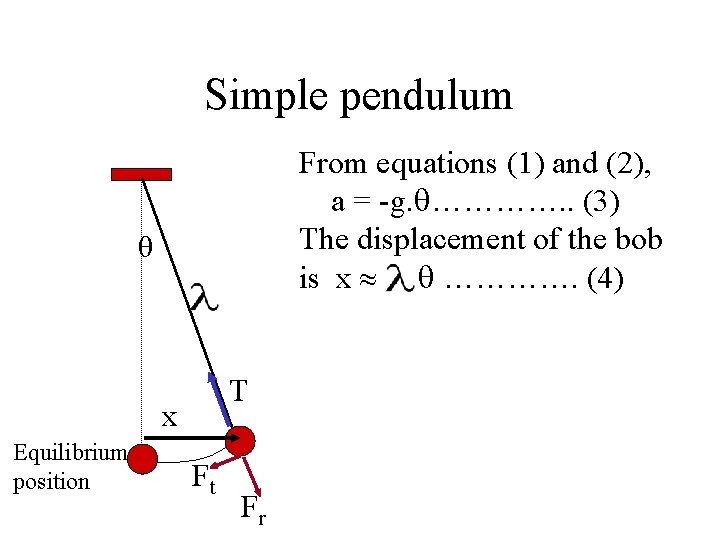
Simple pendulum From equations (1) and (2), a = -g. …………. . (3) The displacement of the bob is x …………. (4) θ T x Equilibrium position Ft Fr

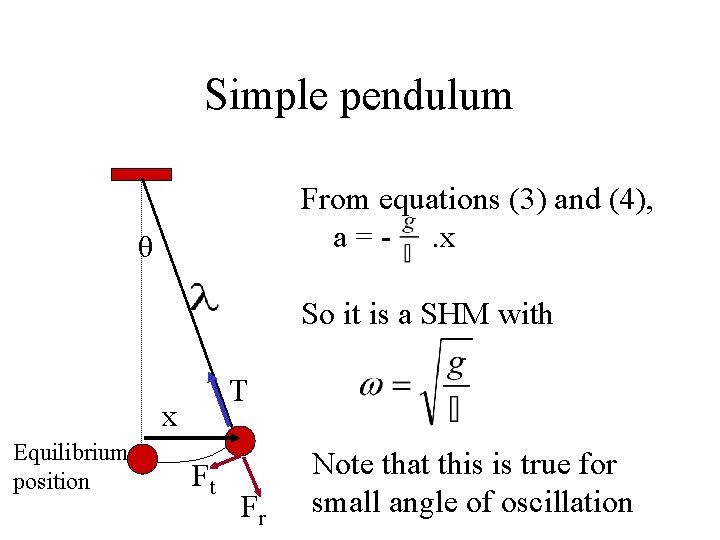
Simple pendulum From equations (3) and (4), a = -. x θ So it is a SHM with T x Equilibrium position Ft Fr Note that this is true for small angle of oscillation

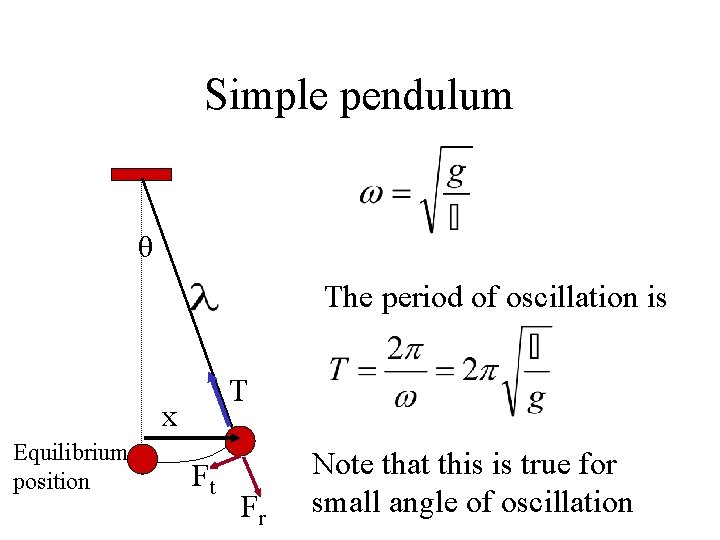
Simple pendulum θ The period of oscillation is T x Equilibrium position Ft Fr Note that this is true for small angle of oscillation

Example 7 • To find the period of a simple pendulum

A floating object • It is a SHM. Floating force In equilibrium water mg

A floating object • It is a SHM. water

A floating object • It is a SHM. water http: //www. deepscience. com/shm. html

Liquid in a U-tube • It is SHM.

Energy in SHM • There is a continuous interchange of kinetic energy and potential energy. • Horizontal Block-spring system – kinetic energy of the block <-> elastic potential energy of the block • Simple pendulum – kinetic energy of the bob <-> gravitational potential energy

Energy in SHM • Kinetic energy is maximum when the particle passes the equilibrium position. • The maximum kinetic energy is

Energy in SHM • Kinetic energy is maximum when the particle passes the equilibrium position. • If we write

Energy in SHM • Kinetic energy is zero when the particle reaches its maximum displacement A. • Kinetic energy is completely transformed into potential energy. • The maximum potential energy Upo is equal to the maximum kinetic energy Uko

Energy in SHM • If the energy is conserved (the motion is undamped), the total energy is Uo = Uko = Upo • At any position, the total energy is

Example 10 • Angular speed of a simple pendulum

Energy versus displacement • When the displacement = x, – the potential energy Up = k. x 2 – the kinetic energy Uk = m. v 2 – the total energy Uo = k. A 2 – Up + Uk = Uo

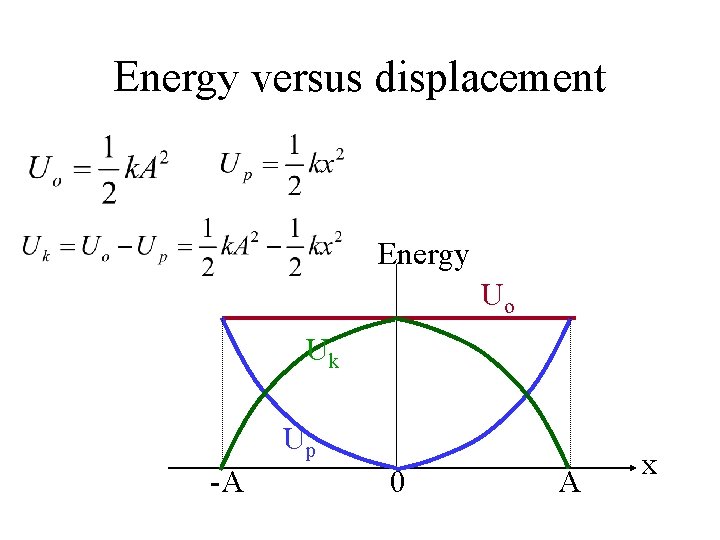
Energy versus displacement Energy Uo Uk Up -A 0 A x

Example 11 • Find the total energy and the maximum speed.

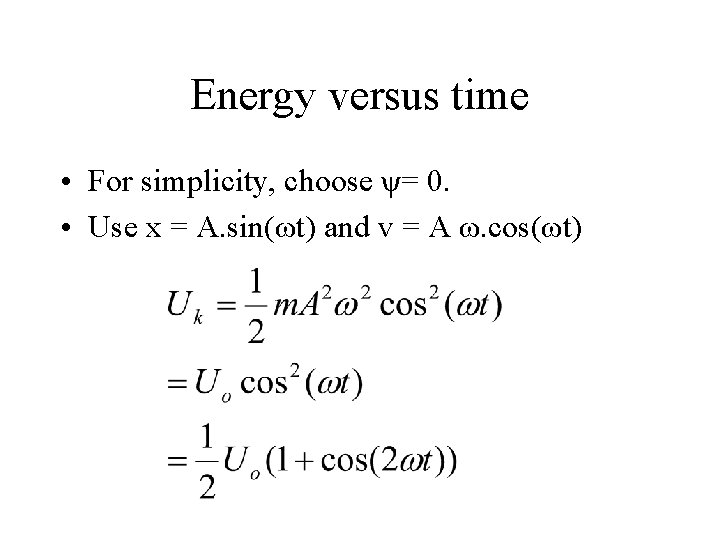
Energy versus time • For simplicity, choose ψ= 0. • Use x = A. sin(ωt) and v = A ω. cos(ωt)

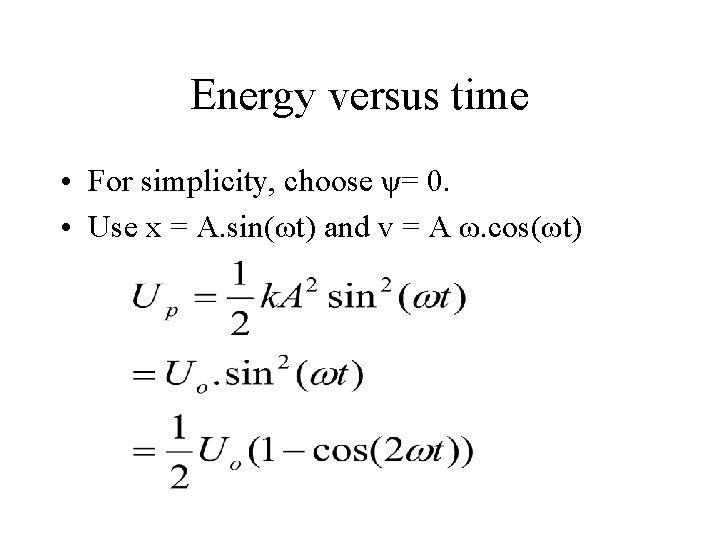
Energy versus time • For simplicity, choose ψ= 0. • Use x = A. sin(ωt) and v = A ω. cos(ωt)

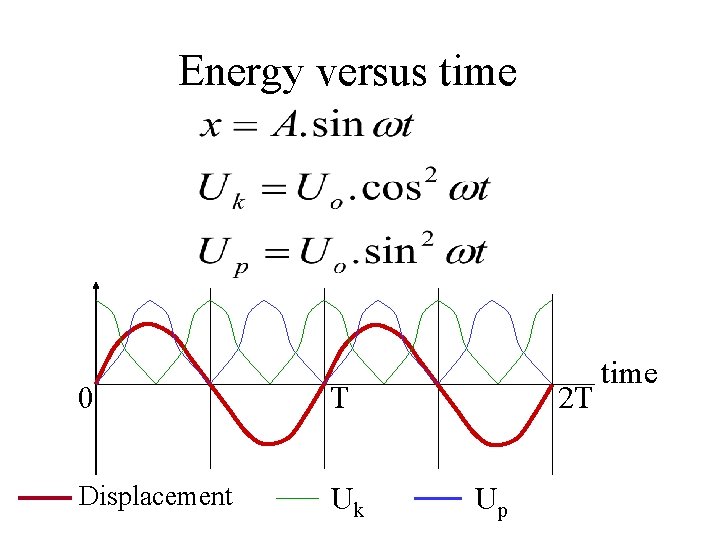
Energy versus time 0 T Displacement Uk 2 T Up time

Damped Oscillation • There is loss of energy in this kind of oscillation due to friction or resistance. • As a result, the amplitude decreases with time. http: //www 3. adnc. com/~topquark/ • There are – Slightly damping fun/JAVA/dho. html – Critical damping http: //www. math. ualberta. ca/~ew – Heavy damping oolgar/java/Hooke. html

Slightly damping • The amplitude decreases exponentially with time. An = A 1. n where is a constant

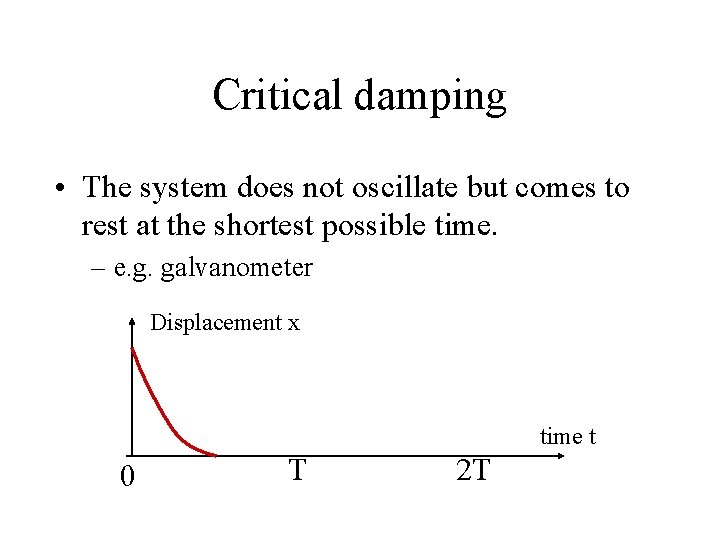
Critical damping • The system does not oscillate but comes to rest at the shortest possible time. – e. g. galvanometer Displacement x time t 0 T 2 T

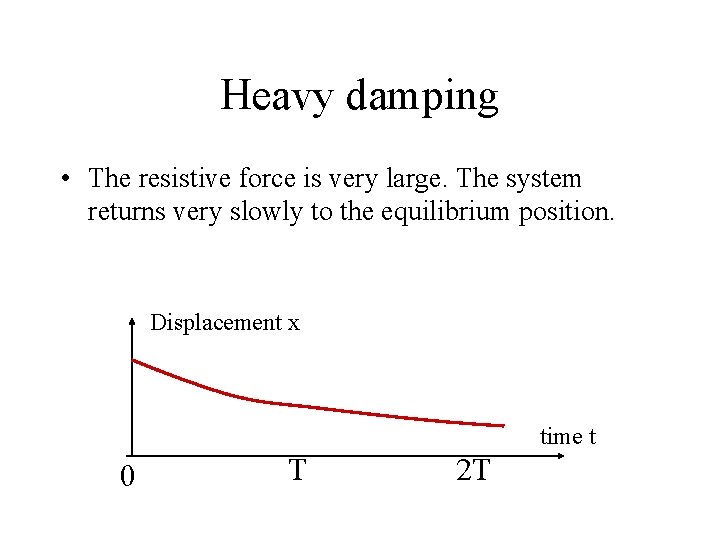
Heavy damping • The resistive force is very large. The system returns very slowly to the equilibrium position. Displacement x time t 0 T 2 T

Example 12 • Slightly damping

Forced oscillations • The vibrating system is acted upon by an external periodic driving force. The system is vibrating at the frequency of the external force. • Without the external driving force, the frequency of free oscillation is called natural frequency. • With the external periodic driving force, the amplitude of vibration varies • http: //physics. uwstout. edu/physapple ts/a-city/physengl/resonance. htm hand vibrating up and down

Forced oscillations • The amplitude of a forced oscillation depends on – damping – frequency of the driving force hand vibrating up and down

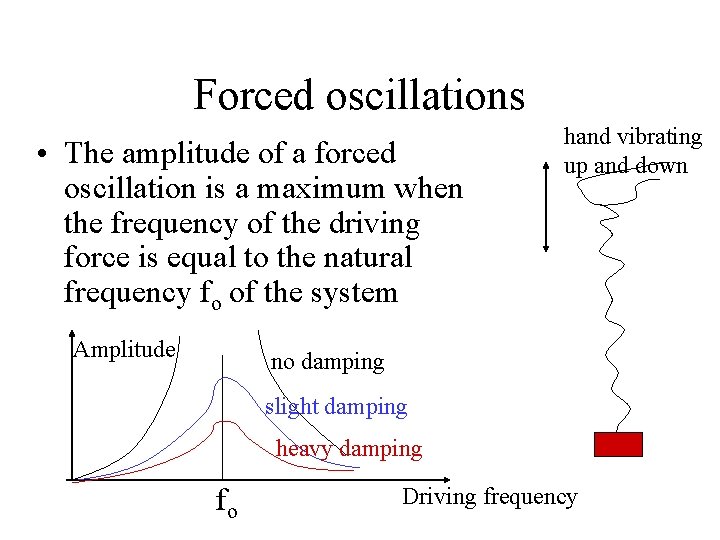
Forced oscillations • The amplitude of a forced oscillation is a maximum when the frequency of the driving force is equal to the natural frequency fo of the system Amplitude hand vibrating up and down no damping slight damping heavy damping fo Driving frequency

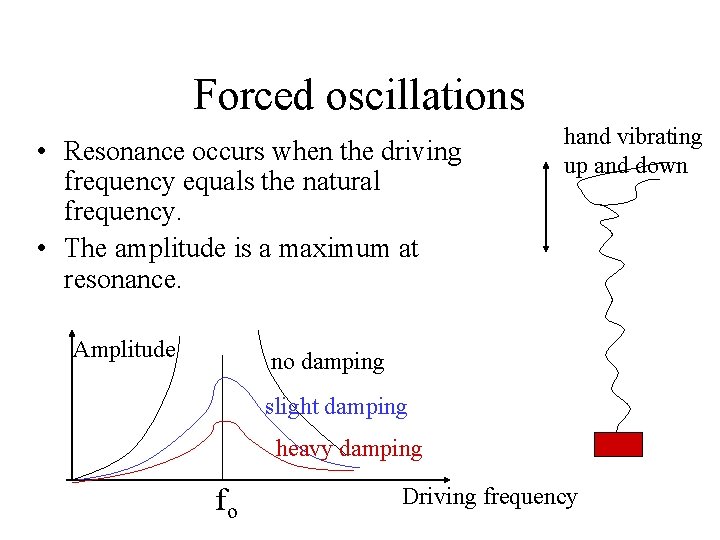
Forced oscillations • Resonance occurs when the driving frequency equals the natural frequency. • The amplitude is a maximum at resonance. Amplitude hand vibrating up and down no damping slight damping heavy damping fo Driving frequency

Phase relationship • When the driving frequency is less than the natural frequency fo of the vibrating system, the two motions are in phase. • When the driving frequency is greater than or equal to the natural frequency fo of the vibrating system, the driven motion always lags behind the driving motion.

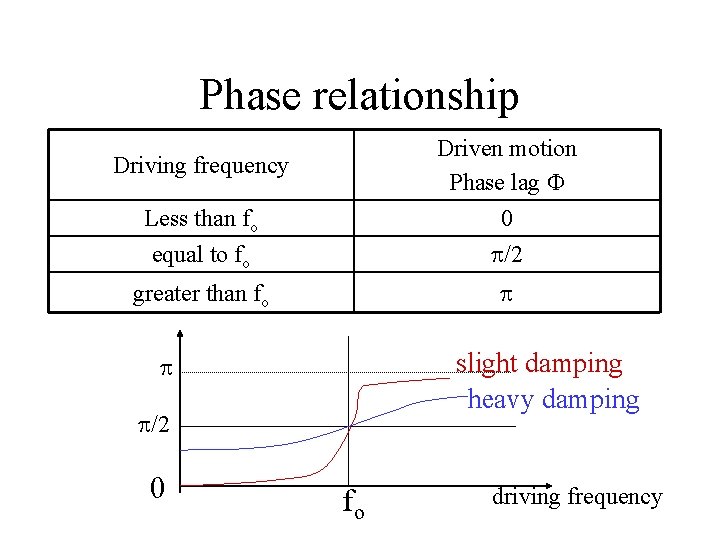
Phase relationship Less than fo Driven motion Phase lag 0 equal to fo /2 greater than fo Driving frequency slight damping heavy damping /2 0 fo driving frequency

Tacoma Narrows Bridge The bridge was driven by the wind.

Tacoma Narrows Bridge The bridge was in resonance with the wind.

Tacoma Narrows Bridge The bridge was in resonance with the wind and finally collapsed.

Why is a simple harmonic motion ‘simple’? • http: //www. physlink. com/ae 135. cfm