Physics at the LHC Monday The standard model

Physics at the LHC • Monday: • The standard model and QCD@LHC • LHC and the Detectors • Tuesday: • The Higgs Boson (theory) • The Top Quark (Arnaud Lucotte, LPSC) • Wednesday • The Higgs Boson (exp) • Higgs+SUSY (theory) • Thursday • 11: 00 LHCb (Frederic Machefert, LAL) • 13: 30 Higgs+SUSY (exp) • Friday • Xtra Dimensions (Gregory Moreau, LPT) • Exotics (Fabienne Ledroit, LPSC)

Supersymmetry • Fermion Boson • has “no” problems with radiative corrections (quadrat. Div. ) • has a light Higgs boson (<135 Ge. V) • promises exciting phenomenology at the Te. V scale 3 neutral Higgs bosons: h, A, H 1 charged Higgs boson: H± and supersymmetric particles: spin-0 Squarks: ~ , ~ q R q. L spin-1/2 spin-1 q Gluino: g~ g Sleptonen: ~ ~ ℓR, ℓL ℓ h, H, A Neutralino χi=1 -4 Z, γ H± Charginos: χ±i=1 -2 W± The parameters of the Higgs sector: • m. A : mass dof the pseudoscalar Higgs Boson • tanβ: ratio of the vacuum expectation values • mass of the top quarks ~ ~ • stop (t. R, t. L) sector: masses and mixing Many different models: • MSSM (minimal supersymmetric extension of the SM, parameter EW Scale) • m. SUGRA (minimal supergravity, GUT Scale) • GMSB • AMB • NMSSM Conservation of R-parity • production of SUSY particles in pairs • (Cascade-) decays to the lightest SUSY particle • LSP stable, neutral and weakly interacting: Neutralino (χ1) • experimental signature: missing ET

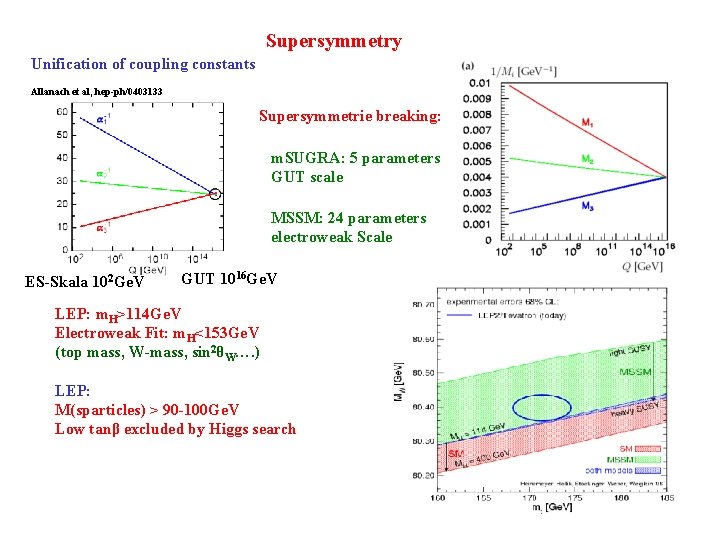
Supersymmetry Unification of coupling constants Allanach et al, hep-ph/0403133 Supersymmetrie breaking: m. SUGRA: 5 parameters GUT scale MSSM: 24 parameters electroweak Scale ES-Skala 102 Ge. V GUT 1016 Ge. V LEP: m. H>114 Ge. V Electroweak Fit: m. H<153 Ge. V (top mass, W-mass, sin 2θW…. ) LEP: M(sparticles) > 90 -100 Ge. V Low tanβ excluded by Higgs search

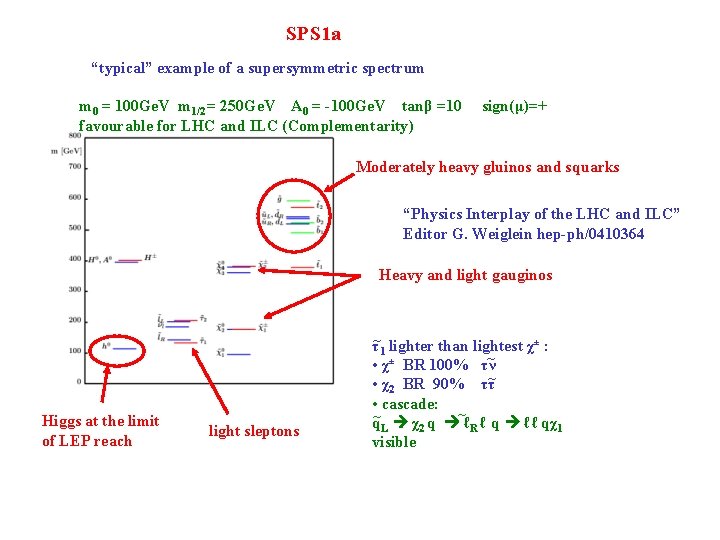
SPS 1 a “typical” example of a supersymmetric spectrum m 0 = 100 Ge. V m 1/2 = 250 Ge. V A 0 = -100 Ge. V tanβ =10 favourable for LHC and ILC (Complementarity) sign(μ)=+ Moderately heavy gluinos and squarks “Physics Interplay of the LHC and ILC” Editor G. Weiglein hep-ph/0410364 Heavy and light gauginos Higgs at the limit of LEP reach light sleptons τ~1 lighter than lightest χ± : ~ • χ± BR 100% τν • χ2 BR 90% ττ~ • cascade: ~ q~L χ2 q ℓR ℓ q ℓ ℓ qχ1 visible

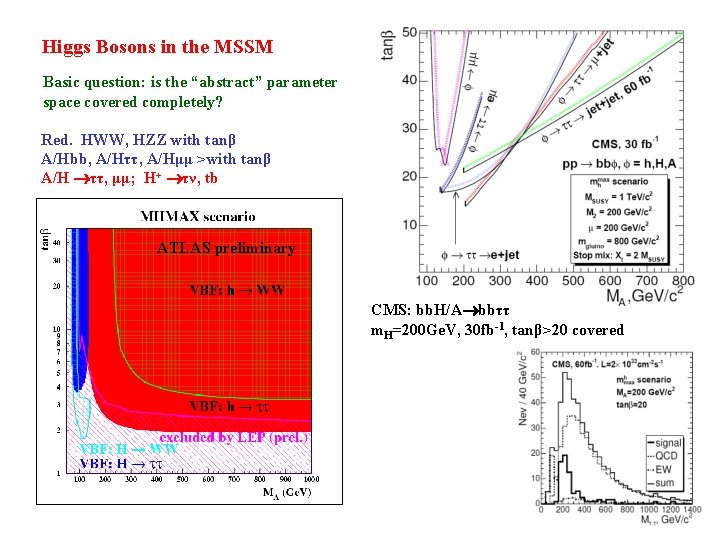
Higgs Bosons in the MSSM Basic question: is the “abstract” parameter space covered completely? Red. HWW, HZZ with tanβ A/Hbb, A/Hττ, A/Hμμ >with tanβ A/H ττ, μμ; H+ τν, tb ATLAS preliminary CMS: bb. H/A bbττ m. H=200 Ge. V, 30 fb-1, tanβ>20 covered

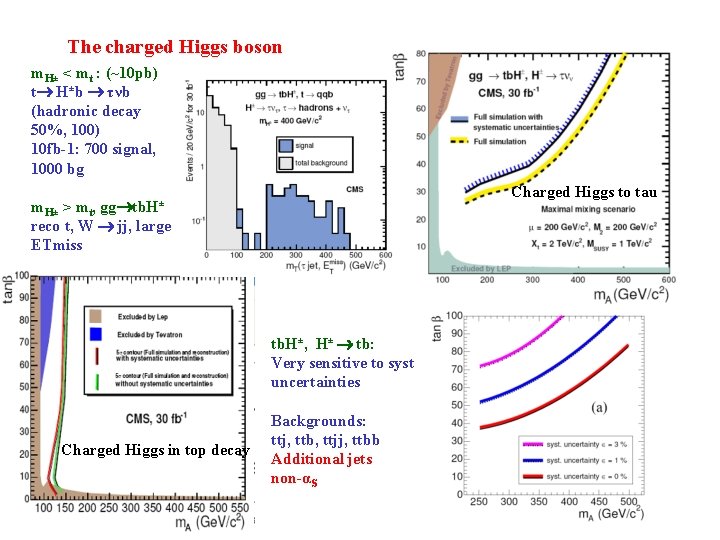
The charged Higgs boson m. H± < mt : (~10 pb) t H±b τνb (hadronic decay 50%, 100) 10 fb-1: 700 signal, 1000 bg Charged Higgs to tau m. H± > mt, gg tb. H± reco t, W jj, large ETmiss tb. H±, H± tb: Very sensitive to syst uncertainties Charged Higgs in top decay Backgrounds: ttj, ttb, ttjj, ttbb Additional jets non-αS

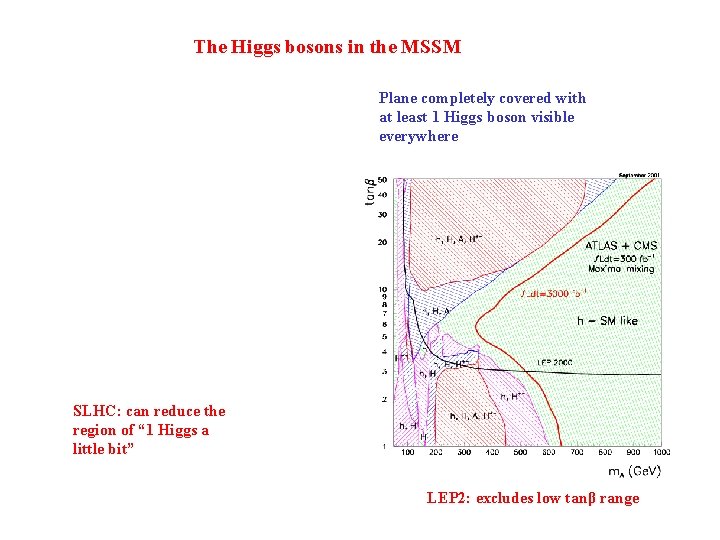
The Higgs bosons in the MSSM Plane completely covered with at least 1 Higgs boson visible everywhere SLHC: can reduce the region of “ 1 Higgs a little bit” LEP 2: excludes low tanβ range

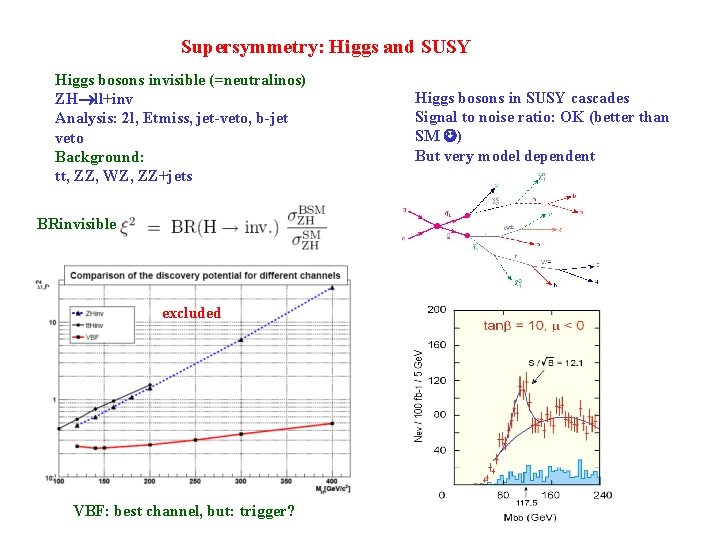
Supersymmetry: Higgs and SUSY Higgs bosons invisible (=neutralinos) ZH ll+inv Analysis: 2 l, Etmiss, jet-veto, b-jet veto Background: tt, ZZ, WZ, ZZ+jets BRinvisible excluded VBF: best channel, but: trigger? Higgs bosons in SUSY cascades Signal to noise ratio: OK (better than SM ) But very model dependent

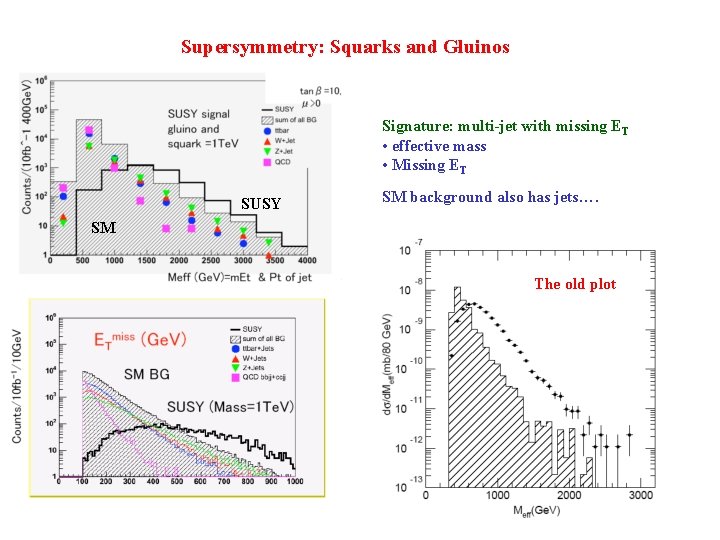
Supersymmetry: Squarks and Gluinos Signature: multi-jet with missing ET • effective mass • Missing ET SUSY SM background also has jets…. SM The old plot

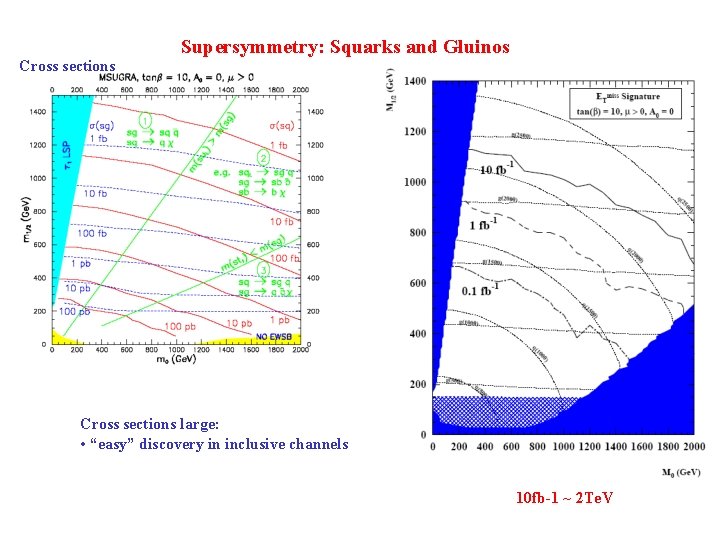
Cross sections Supersymmetry: Squarks and Gluinos Cross sections large: • “easy” discovery in inclusive channels 10 fb-1 ~ 2 Te. V

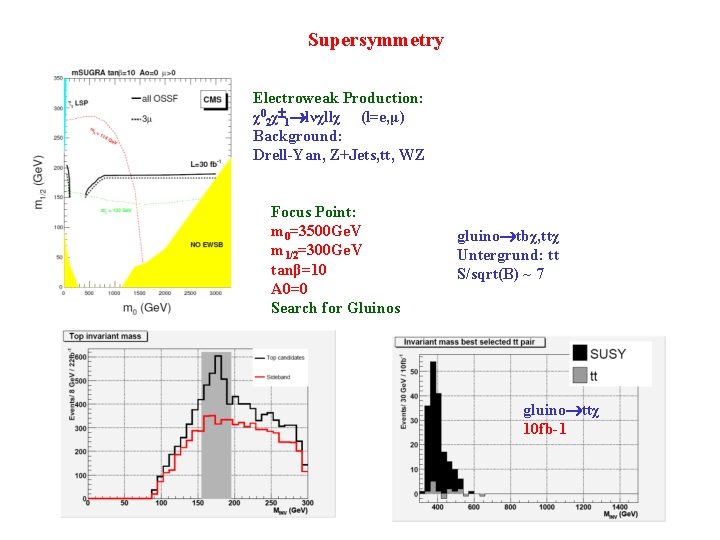
Supersymmetry Electroweak Production: χ02χ 1 lνχllχ (l=e, μ) Background: Drell-Yan, Z+Jets, tt, WZ Focus Point: m 0=3500 Ge. V m 1/2=300 Ge. V tanβ=10 A 0=0 Search for Gluinos gluino tbχ, ttχ Untergrund: tt S/sqrt(B) ~ 7 gluino ttχ 10 fb-1

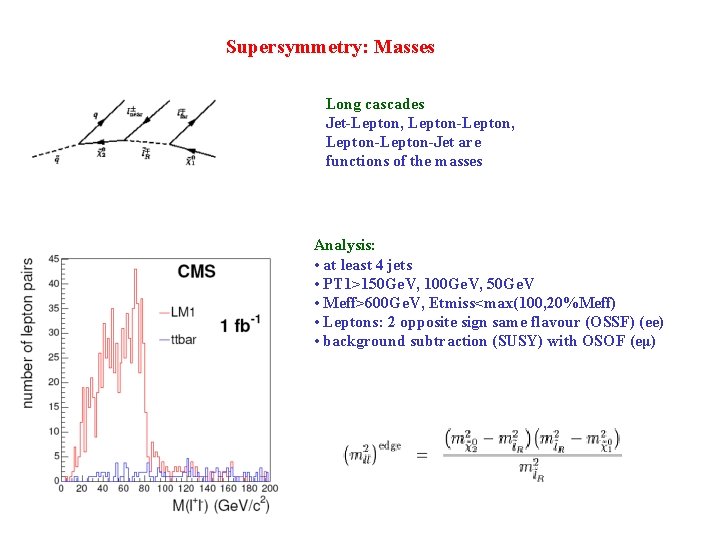
Supersymmetry: Masses Long cascades Jet-Lepton, Lepton-Lepton-Jet are functions of the masses Analysis: • at least 4 jets • PT 1>150 Ge. V, 100 Ge. V, 50 Ge. V • Meff>600 Ge. V, Etmiss<max(100, 20%Meff) • Leptons: 2 opposite sign same flavour (OSSF) (ee) • background subtraction (SUSY) with OSOF (eμ)

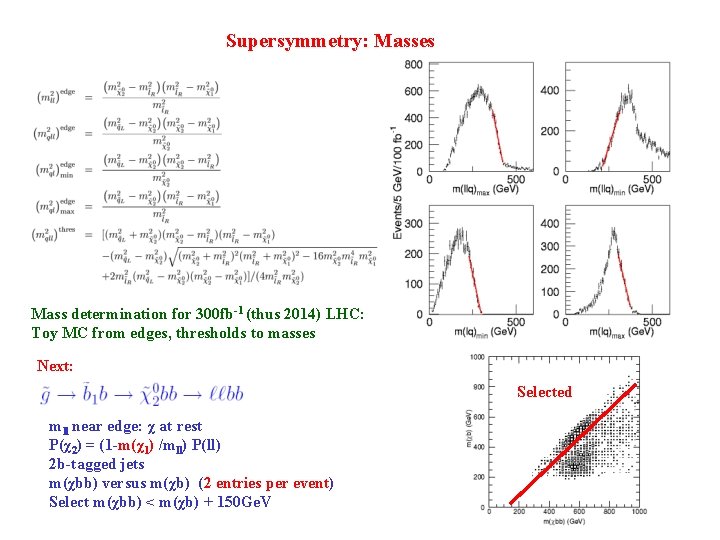
Supersymmetry: Masses Mass determination for 300 fb-1 (thus 2014) LHC: Toy MC from edges, thresholds to masses Next: Selected mll near edge: χ at rest P(χ2) = (1 -m(χ1) /mll) P(ll) 2 b-tagged jets m(χbb) versus m(χb) (2 entries per event) Select m(χbb) < m(χb) + 150 Ge. V

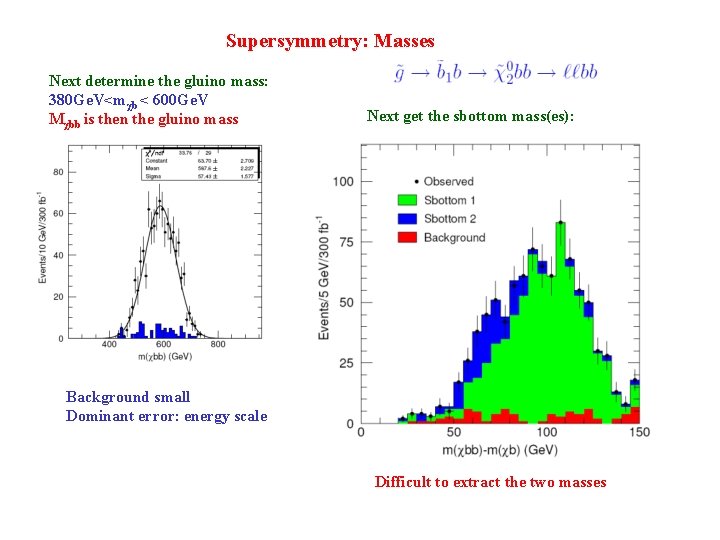
Supersymmetry: Masses Next determine the gluino mass: 380 Ge. V<mχb < 600 Ge. V Mχbb is then the gluino mass Next get the sbottom mass(es): Background small Dominant error: energy scale Difficult to extract the two masses

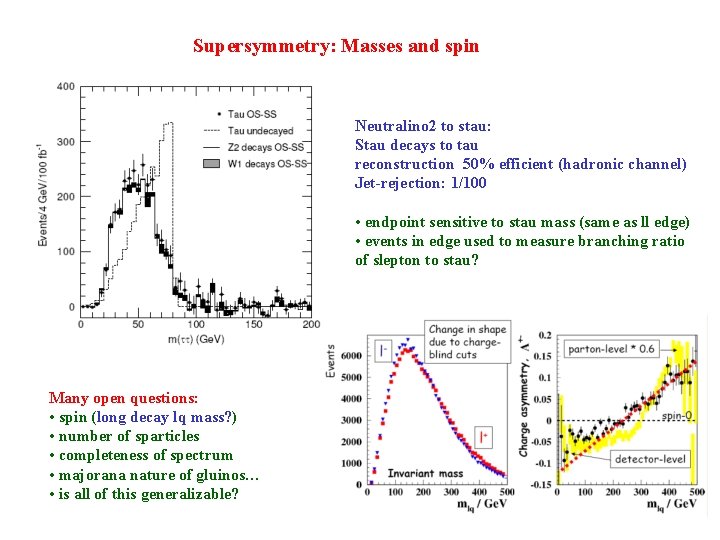
Supersymmetry: Masses and spin Neutralino 2 to stau: Stau decays to tau reconstruction 50% efficient (hadronic channel) Jet-rejection: 1/100 • endpoint sensitive to stau mass (same as ll edge) • events in edge used to measure branching ratio of slepton to stau? Many open questions: • spin (long decay lq mass? ) • number of sparticles • completeness of spectrum • majorana nature of gluinos… • is all of this generalizable?

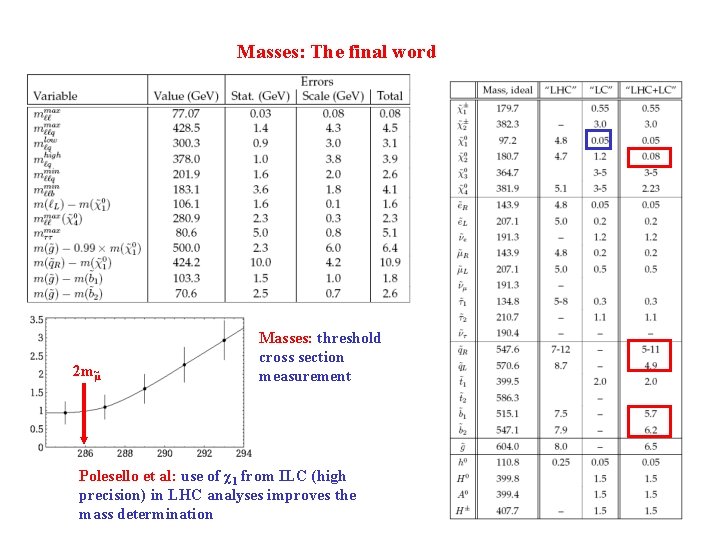
Masses: The final word 2 m~μ Masses: threshold cross section measurement Polesello et al: use of χ1 from ILC (high precision) in LHC analyses improves the mass determination

Determining the underlying parameters Transform (s)particle properties to fundamental parameters: • m. SUGRA (top-down) and MSSM (bottom-up) with conservation of R-parity Beenakker et al • need predictions for all observables matching theoretical and experimental precision • observables sensitive to several parameters: correlations, error propagation Brain power and sophisticated tools: • Mass spectra generated by SOFTSUSY, SUSPECT, SPHENO • Branching ratios by MSMLIB, SPHENO, SDecay • e+e- cross sections (polarized) by SPHENO • NLO proton cross sections by Prospino 2. 0 Putting it all together (error propagation, search for minima etc): FITTINO and SFITTER P. Skands et al. , SUSY Les Houches accord (SLHA), Interfacing SUSY spectrum calculators, decay packages, and event generators, JHEP 0407 (2004) 036

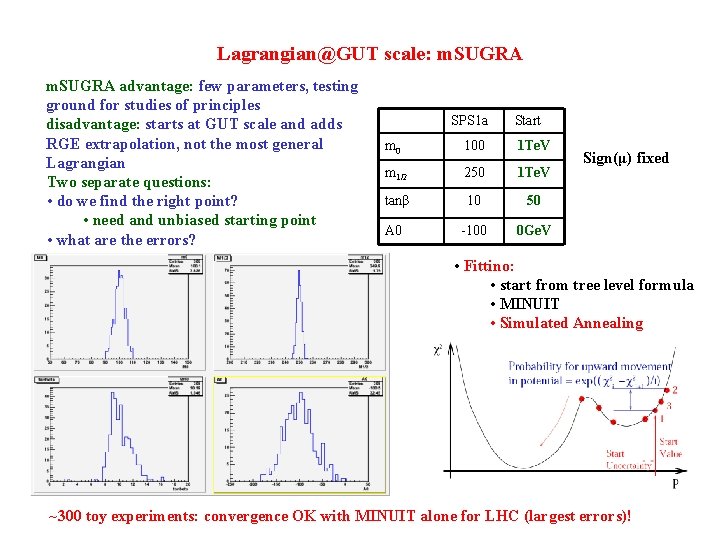
Lagrangian@GUT scale: m. SUGRA advantage: few parameters, testing ground for studies of principles disadvantage: starts at GUT scale and adds RGE extrapolation, not the most general Lagrangian Two separate questions: • do we find the right point? • need and unbiased starting point • what are the errors? SPS 1 a Start m 0 100 1 Te. V m 1/2 250 1 Te. V tanβ 10 50 A 0 -100 0 Ge. V Sign(μ) fixed • Fittino: • start from tree level formula • MINUIT • Simulated Annealing ~300 toy experiments: convergence OK with MINUIT alone for LHC (largest errors)!

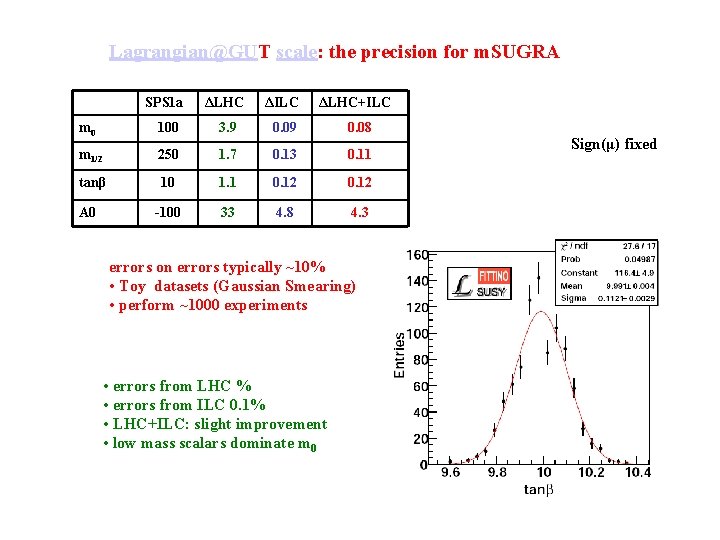
Lagrangian@GUT scale: the precision for m. SUGRA SPS 1 a ΔLHC ΔILC m 0 100 3. 9 0. 08 m 1/2 250 1. 7 0. 13 0. 11 tanβ 10 1. 1 0. 12 -100 33 4. 8 4. 3 A 0 ΔLHC+ILC errors on errors typically ~10% • Toy datasets (Gaussian Smearing) • perform ~1000 experiments • errors from LHC % • errors from ILC 0. 1% • LHC+ILC: slight improvement • low mass scalars dominate m 0 Sign(μ) fixed

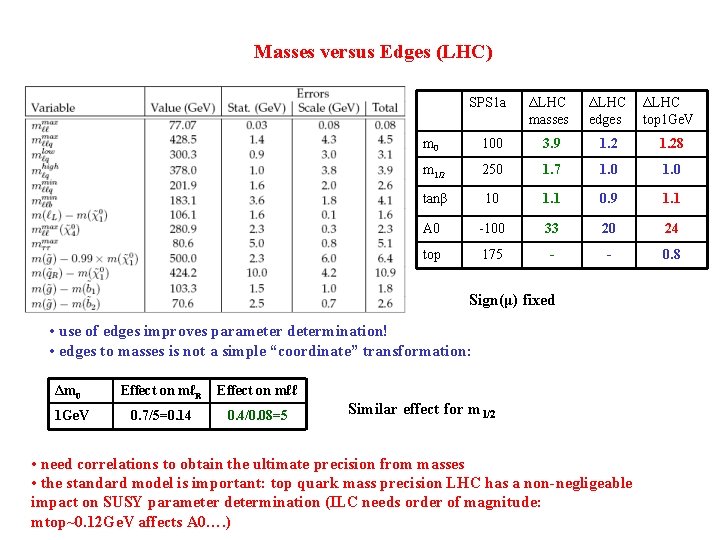
Masses versus Edges (LHC) SPS 1 a ΔLHC masses ΔLHC edges ΔLHC top 1 Ge. V m 0 100 3. 9 1. 28 m 1/2 250 1. 7 1. 0 tanβ 10 1. 1 0. 9 1. 1 A 0 -100 33 20 24 top 175 - - 0. 8 Sign(μ) fixed • use of edges improves parameter determination! • edges to masses is not a simple “coordinate” transformation: Δm 0 1 Ge. V Effect on mℓR Effect on mℓℓ 0. 7/5=0. 14 0. 4/0. 08=5 Similar effect for m 1/2 • need correlations to obtain the ultimate precision from masses • the standard model is important: top quark mass precision LHC has a non-negligeable impact on SUSY parameter determination (ILC needs order of magnitude: mtop~0. 12 Ge. V affects A 0…. )

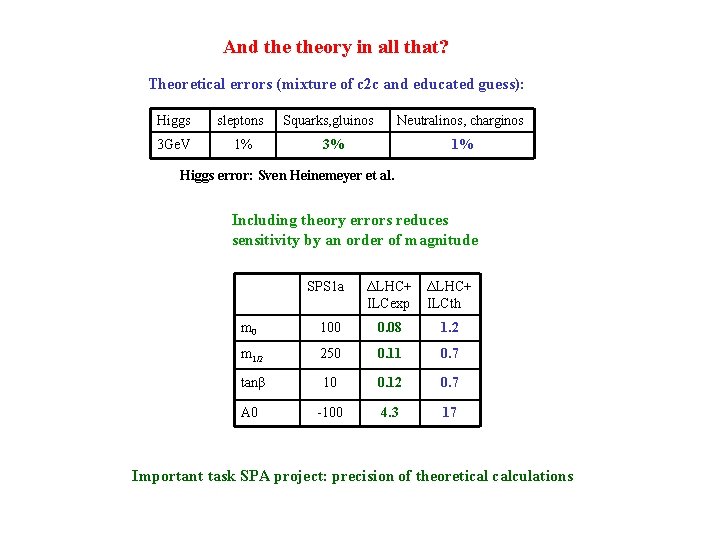
And theory in all that? Theoretical errors (mixture of c 2 c and educated guess): Higgs sleptons 3 Ge. V 1% Squarks, gluinos Neutralinos, charginos 3% 1% Higgs error: Sven Heinemeyer et al. Including theory errors reduces sensitivity by an order of magnitude SPS 1 a ΔLHC+ ILCexp ΔLHC+ ILCth m 0 100 0. 08 1. 2 m 1/2 250 0. 11 0. 7 tanβ 10 0. 12 0. 7 A 0 -100 4. 3 17 Important task SPA project: precision of theoretical calculations

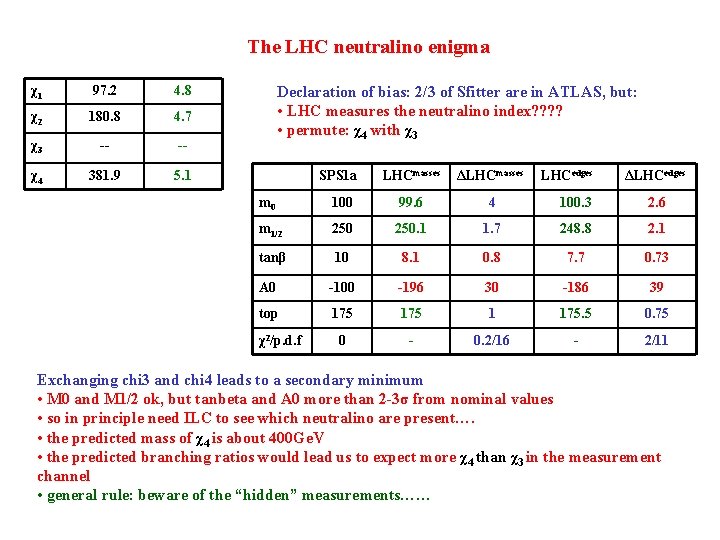
The LHC neutralino enigma χ1 97. 2 4. 8 χ2 180. 8 4. 7 χ3 -- -- χ4 381. 9 5. 1 Declaration of bias: 2/3 of Sfitter are in ATLAS, but: • LHC measures the neutralino index? ? • permute: χ4 with χ3 SPS 1 a LHCmasses ΔLHCmasses m 0 100 99. 6 4 100. 3 2. 6 m 1/2 250. 1 1. 7 248. 8 2. 1 tanβ 10 8. 1 0. 8 7. 7 0. 73 A 0 -100 -196 30 -186 39 top 175 1 175. 5 0. 75 0 - 0. 2/16 - 2/11 χ2/p. d. f LHCedges ΔLHCedges Exchanging chi 3 and chi 4 leads to a secondary minimum • M 0 and M 1/2 ok, but tanbeta and A 0 more than 2 -3σ from nominal values • so in principle need ILC to see which neutralino are present…. • the predicted mass of χ4 is about 400 Ge. V • the predicted branching ratios would lead us to expect more χ4 than χ3 in the measurement channel • general rule: beware of the “hidden” measurements……

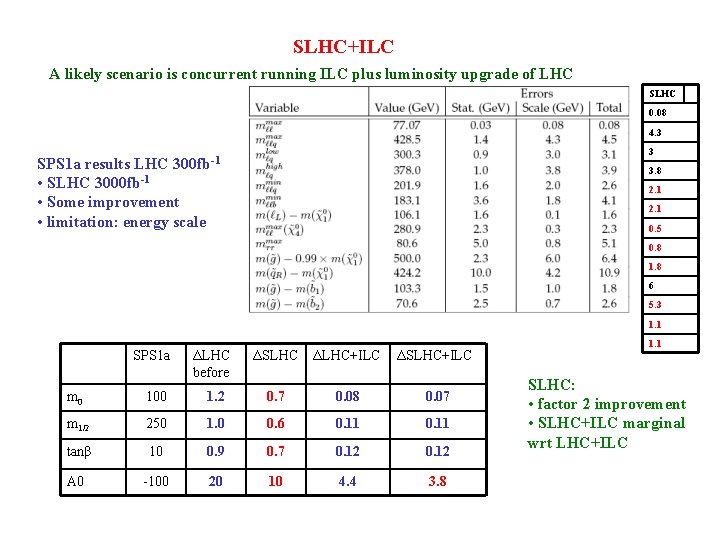
SLHC+ILC A likely scenario is concurrent running ILC plus luminosity upgrade of LHC SLHC 0. 08 4. 3 3 300 fb-1 SPS 1 a results LHC • SLHC 3000 fb-1 • Some improvement • limitation: energy scale 3. 8 2. 1 0. 5 0. 8 1. 8 6 5. 3 1. 1 SPS 1 a ΔLHC before ΔSLHC ΔLHC+ILC ΔSLHC+ILC m 0 100 1. 2 0. 7 0. 08 0. 07 m 1/2 250 1. 0 0. 6 0. 11 tanβ 10 0. 9 0. 7 0. 12 A 0 -100 20 10 4. 4 3. 8 1. 1 SLHC: • factor 2 improvement • SLHC+ILC marginal wrt LHC+ILC

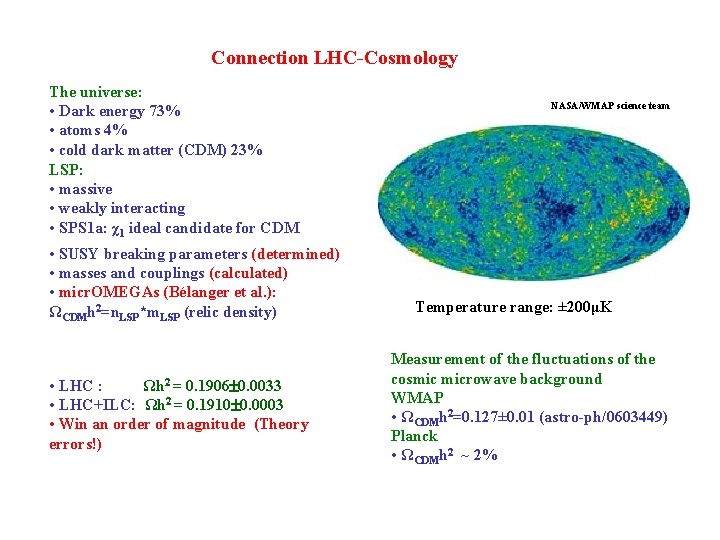
Connection LHC-Cosmology The universe: • Dark energy 73% • atoms 4% • cold dark matter (CDM) 23% LSP: • massive • weakly interacting • SPS 1 a: χ1 ideal candidate for CDM • SUSY breaking parameters (determined) • masses and couplings (calculated) • micr. OMEGAs (Bélanger et al. ): ΩCDMh 2=n. LSP*m. LSP (relic density) • LHC : Ωh 2 = 0. 1906 0. 0033 • LHC+ILC: Ωh 2 = 0. 1910 0. 0003 • Win an order of magnitude (Theory errors!) NASA/WMAP science team Temperature range: ± 200μK Measurement of the fluctuations of the cosmic microwave background WMAP • ΩCDMh 2=0. 127± 0. 01 (astro-ph/0603449) Planck • ΩCDMh 2 ~ 2%

LHC ILC CLIC ILC LHC MSSM CLIC LHC MSSM which MSSM? ? 24 parameters at the EW scale SFitter choice: do not unify 1 st and 2 nd generation: data should tell us … LHC or ILC alone: • certain parameters must be fixed LHC+ILC: • all parameters fitted • several parameters improved CLIC wrt ILC: • no fixed parameters with good precision LHC+CLIC • improvement essentially in the squark sector with factor 2 -3 on errors as expected from the mass measurement improvement wrt LHC Note: if at LHC m. SUGRA has a secondary minimum, MSSM will have even more…. .

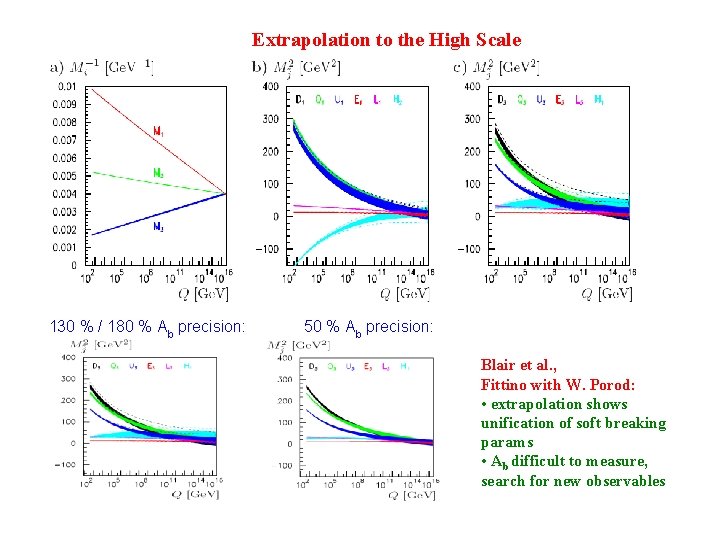
Extrapolation to the High Scale 130 % / 180 % Ab precision: 50 % Ab precision: Blair et al. , Fittino with W. Porod: • extrapolation shows unification of soft breaking params • Ab difficult to measure, search for new observables

Summary • Higgs: at least one Higgs boson can be found everywhere • additional Higgs channels open • squarks and gluinos: clearest signal • tri-lepton signal difficult • Above all that: it’s difficult, exciting, therefore hope for an early discovery of SUSY at the LHC soon…. .