Physics and the Quantum Mechanical Model Light Electrons

Physics and the Quantum Mechanical Model

Light • Electrons in atoms are arranged in orbitals, each with a particular energy level. When the electrons go to another energy level they either absorb or emit energy. • Emitting energy produces light.

Light • The quantum mechanical model grew out of the study of light. • By 1900 light was known to consist of particles and waves.

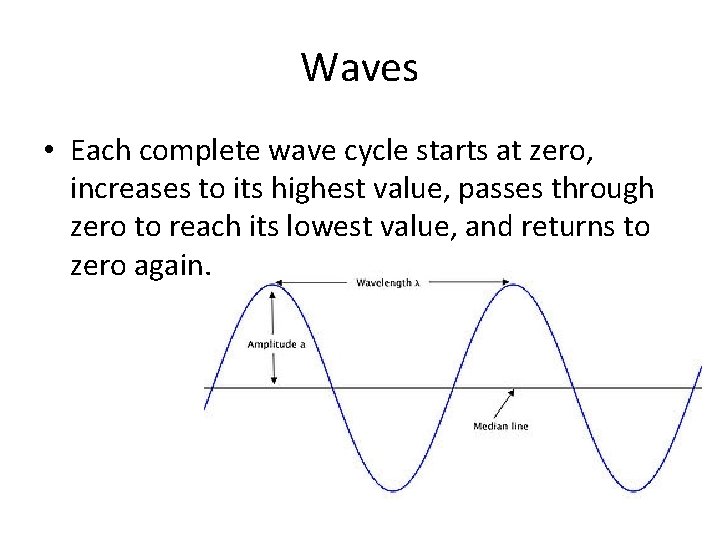
Waves • Each complete wave cycle starts at zero, increases to its highest value, passes through zero to reach its lowest value, and returns to zero again.

Waves • The amplitude of a wave is the wave’s height from zero to the crest. • The amplitude represents energy and is measured in meters.

Waves • The wavelength, represented by lambda (λ), is the distance between the crests.

Waves • The frequency is the number of wave cycles to pass a given point per unit of time. • The frequency are usually cycles per second and is represented by the letter v. • The SI unit of cycles per second is called a hertz (Hz).

Waves • The speed of light is calculated by: • C = λv • The frequency and wavelength of light are inversely proportional to each other. • As the wavelength of light increases, the frequency decreases.

Waves • According to the wave model, light consists of electromagnetic (EM) waves. • Electromagnetic radiation includes radio waves, microwaves, infrared waves, visible light, ultraviolet waves, x-rays, and gamma rays. • All EM waves travel in a vacuum at a speed of 2. 998 x 108 m/s.

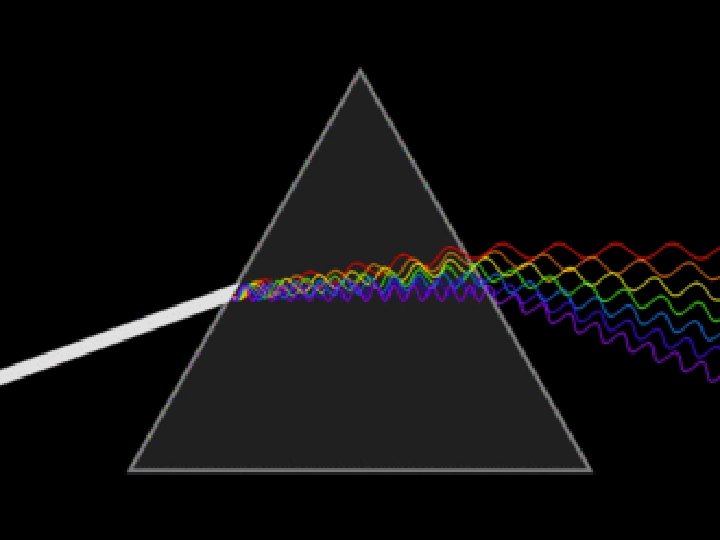
Waves • Sunlight consists of light with a continuous range of wavelengths and frequencies. • The color of light found in sunlight depends on its frequency. • When sunlight passes through a prism, the different frequencies separate into a spectrum of colors.

Waves • A rainbow is an example of a spectrum each tiny droplet of water acts as a prism to produce a spectrum.

Waves • In the visible spectrum (ROYGBIV), red light has the longest wavelength and the lowest frequency.

Calculating the Wavelength of Light • Calculate the wavelength of the yellow light emitted by the sodium lamp if the frequency of the radiation is 5. 10 x 1014 Hz. • c = λv • λ= c/v = (3. 0 x 108 m/s) / (5. 10 x 1014 Hz) • Λ = 5. 88 x 10 -7 m/s

Calculating the Wavelength of Light • 1. What is the wavelength of radiation with a frequency of 1. 50 x 1013 Hz? Does this radiation have a longer or shorter wavelength than red light? • 2. what frequency is radiation with a wavelength of 5. 00 x 10 -8 m? in what region of the EM spectrum is this radiation?

Atomic Spectra • Atoms absorb energy that raises electrons into higher energy levels, and then lose the energy by emitting light when electrons return to lower energy levels.

Atomic Spectra • Unlike sunlight, the light emitted by atoms consists of a mixture of only specific frequencies and is not a mixture of all visible frequencies. • Each specific frequency of visible light emitted corresponds to a particular color.

Atomic Spectra • When light passes through a prism the frequencies of light emitted by an element separate to give the atomic emission spectrum of the element. • No two elements have the same emission spectrum.

Atomic Spectra • Bohr’s model not only explained why the emission spectrum of hydrogen consists of specific frequencies of light. • It also predicted specific values of these frequencies.

Atomic Spectra • In the Bohr model, the lone electron in the hydrogen atom can have only certain specific energies. • The lowest possible energy of the electron is its ground state.

Atomic Spectra • In the ground state, the electron’s principal quantum number (n) is 1. • Excitation of the electron by absorbing energy raises it from the ground state to an excited state with n = 2, 3, 4, 5, or 6 and so forth.

Atomic Spectra • A quantum of energy in the form of light is emitted when the electron drops back to a lower energy level. • This emission is called an electronic transition.

Atomic Spectra • Bohr knew that this quantum of energy, E, is related to the frequency, v, of the emitted light by the equation: • E=hxv • H = 6. 262 x 10 -34 J·s

Atomic Spectra • The light emitted by an electronic transition from a higher to a lower energy level has a frequency directly proportional to the energy change of the electron.

Atomic Spectra • Bohr’s theory of the atom was only partially right. It explained the emission spectrum of hydrogen but not the emission spectra of atoms with more than one electron. • The quantum mechanical model replaced the Bohr model of the atom and is based on the description of the motion of material obejcts as waves.

Quantum Mechanics • Einstein successfully explained experimental data by proposing that light could be described as quanta of energy that behave as if they were particles. • Light quanta are called photons.

Quantum Mechanics • Classical mechanics adequately describes the motions of bodies much larger than atoms, while quantum mechanics describes the motions of subatomic particles and atoms as waves.

Quantum Mechanics • The Heisenberg uncertainty principle states that it is impossible to know exactly both the velocity and the position of a particles at the same time.