Physics and Physical Measurement Topic 1 3 Scalars

Physics and Physical Measurement Topic 1. 3 Scalars and Vectors

Scalars Quantities b Scalars can be completely described by magnitude (size) b Scalars can be added algebraically b They are expressed as positive or negative numbers and a unit b examples include : - mass, electric charge, distance, speed, energy

Vector Quantities b Vectors need both a magnitude and a direction to describe them (also a point of application) b When expressing vectors as a symbol, you need to adopt a recognized notation b e. g. b They need to be added, subtracted and multiplied in a special way b Examples : - velocity, weight, acceleration, displacement, momentum, force

Addition and Subtraction b The Resultant (Net) is the result vector that comes from adding or subtracting a number of vectors b If vectors have the same or opposite directions the addition can be done simply b same direction : add b opposite direction : subtract

Co-planar vectors b The addition of co-planar vectors that do not have the same or opposite direction can be solved by using scale drawings to get an accurate resultant b Or if an estimation is required, they can be drawn roughly b or by Pythagoras’ theorem and trigonometry b Vectors can be represented by a straight line segment with an arrow at the end

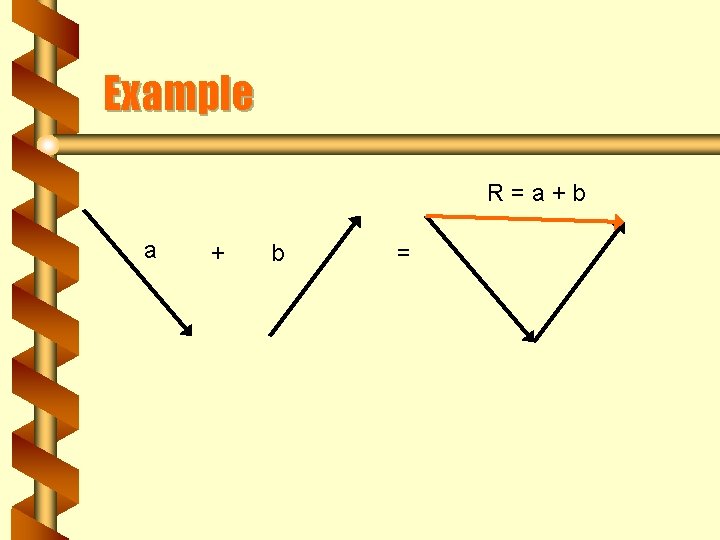
Triangle of Vectors b Two vectors are added by drawing to scale and with the correct direction the two vectors with the tail of one at the tip of the other. b The resultant vector is the third side of the triangle and the arrow head points in the direction from the ‘free’ tail to the ‘free’ tip

Example R=a+b a + b =

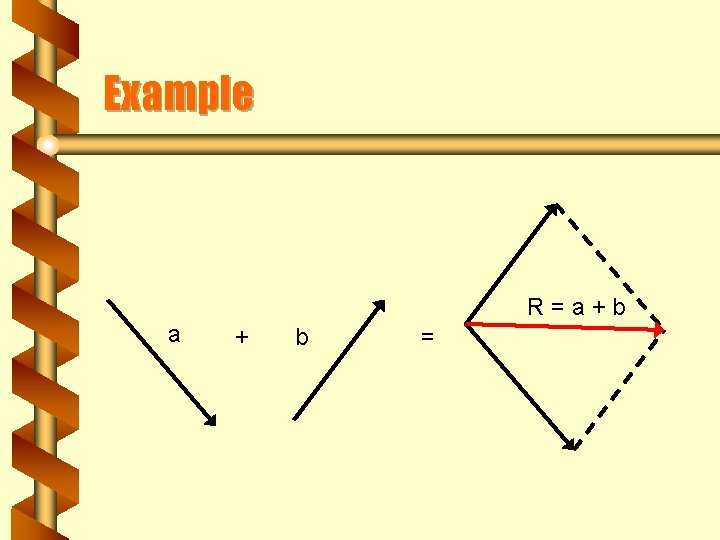
Parallelogram of Vectors b Place the two vectors tail to tail, to scale and with the correct directions b Then complete the parallelogram b The diagonal starting where the two tails meet and finishing where the two arrows meet becomes the resultant vector

Example R=a+b a + b =

More than 2 b If there are more than 2 co-planar vectors to be added, place them all head to tail to form polygon when the resultant is drawn from the ‘free’ tail to the ‘free’ tip. b Notice that the order doesn’t matter!

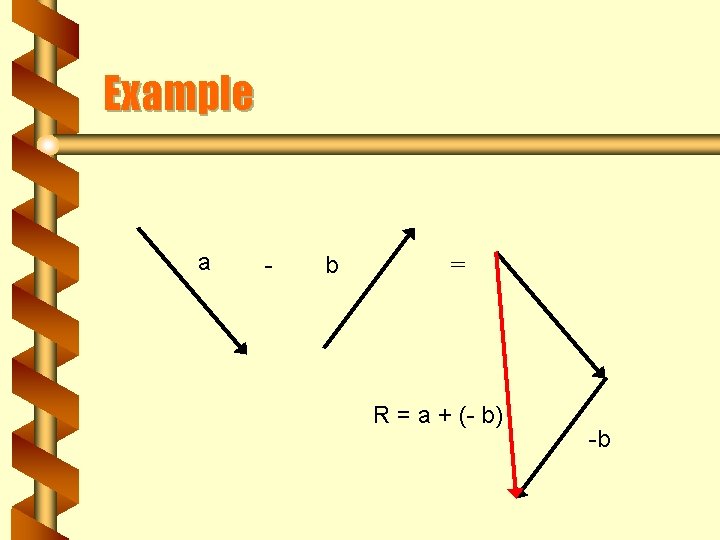
Subtraction of Vectors b To subtract a vector, you reverse the direction of that vector to get the negative of it b Then you simply add that vector

Example a - b = R = a + (- b) -b

Multiplying Scalars b Scalars are multiplied and divided in the normal algebraic manner b Do not forget units! b 5 m / 2 s = 2. 5 ms-1 b 2 k. W x 3 h = 6 k. Wh (kilowatt-hours)

Multiplying Vectors b A vector multiplied by a scalar gives a vector with the same direction as the vector and magnitude equal to the product of the scalar and a vector magnitude b A vector divided by a scalar gives a vector with same direction as the vector and magnitude equal to the vector magnitude divided by the scalar b You don’t need to be able to multiply a vector by another vector

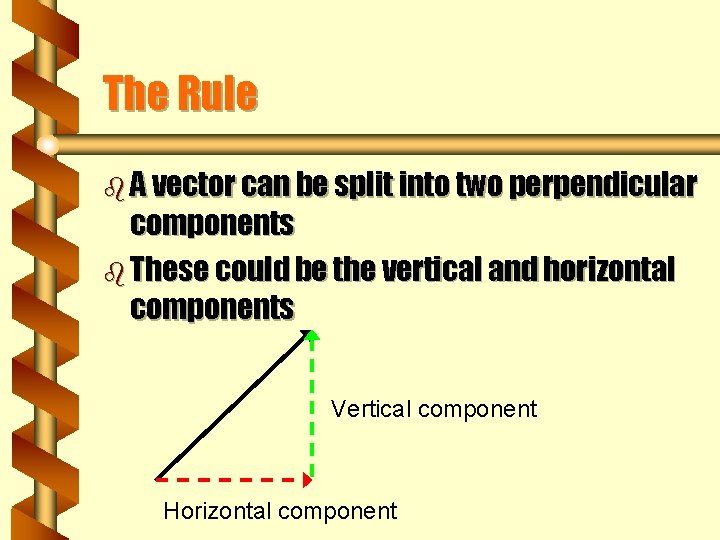
Resolving Vectors b The process of finding the Components of vectors is called Resolving vectors b Just as 2 vectors can be added to give a resultant, a single vector can be split into 2 components or parts

The Rule b A vector can be split into two perpendicular components b These could be the vertical and horizontal components Vertical component Horizontal component

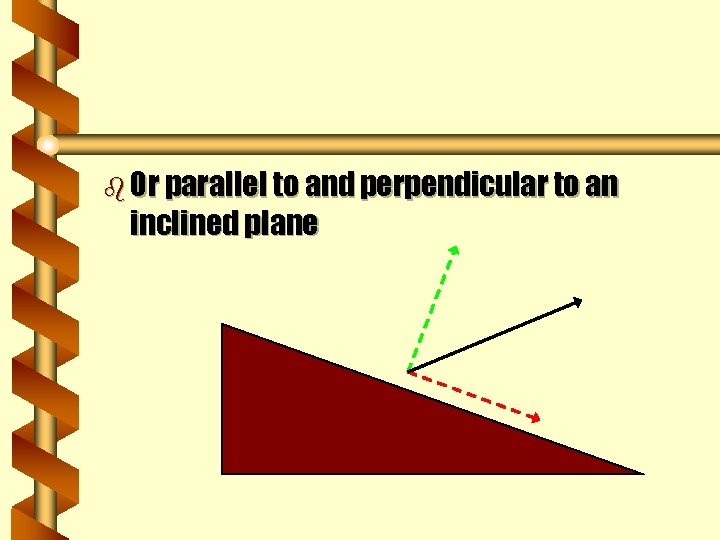
b Or parallel to and perpendicular to an inclined plane

b These vertical and horizontal components could be the vertical and horizontal components of velocity for projectile motion b Or the forces perpendicular to and along an inclined plane

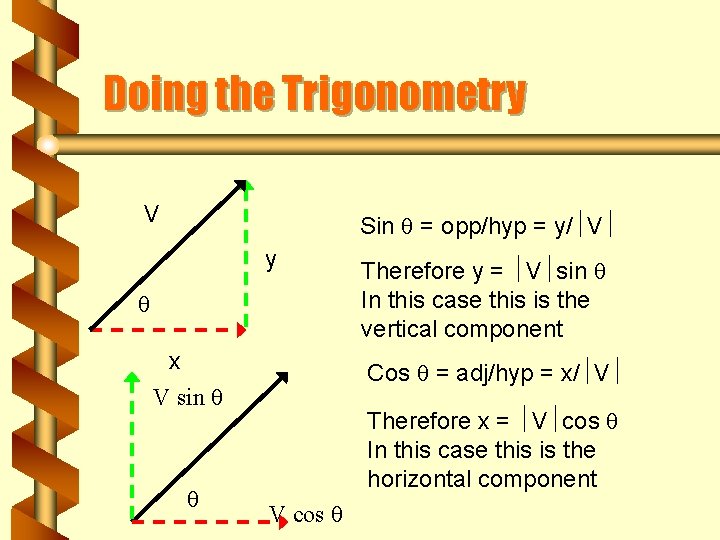
Doing the Trigonometry V Sin = opp/hyp = y/ V y x V sin Therefore y = V sin In this case this is the vertical component Cos = adj/hyp = x/ V Therefore x = V cos In this case this is the horizontal component V cos

Quick Way b If you resolve through the angle it is b cos b If you resolve ‘not’ through the angle it is b sin

Adding 2 or More Vectors by Components b First resolve into components (making sure that all are in the same 2 directions) b Then add the components in each of the 2 directions b Recombine them into a resultant vector b This will involve using Pythagoras´ theorem

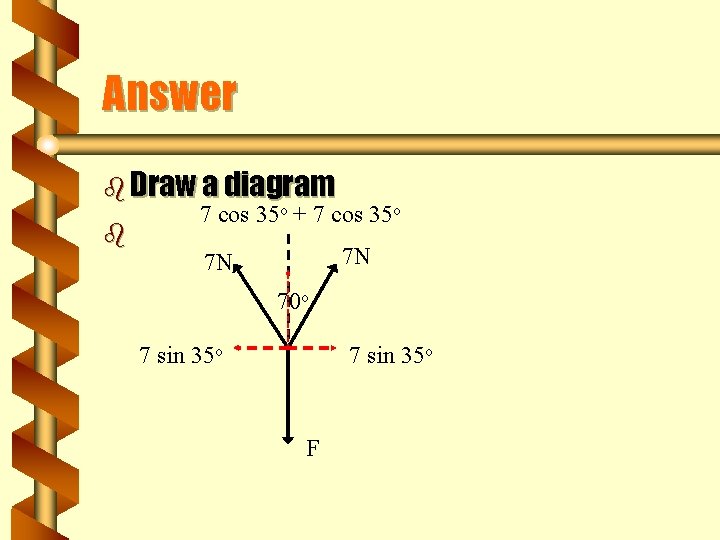
Question b Three strings are attached to a small metal ring. 2 of the strings make an angle of 70 o and each is pulled with a force of 7 N. b What force must be applied to the 3 rd string to keep the ring stationary?

Answer b Draw a diagram 7 cos 35 o + 7 cos 35 o b 7 N 7 N 70 o 7 sin 35 o F

b Horizontally b 7 sin 35 o - 7 sin 35 o = 0 b Vertically b 7 cos 35 o + 7 cos 35 o = F b F = 11. 5 N b And at what angle? b 145 o to one of the strings.