PHYSICS 231 INTRODUCTORY PHYSICS I www pa msu

PHYSICS 231 INTRODUCTORY PHYSICS I www. pa. msu. edu/courses/phy 231 Scott Pratt prattsc@msu. edu (517) 355 -9200, ext. 2016 Office Hours: Monday, 9 -10: 30 AM in 1248 BPS

Course Information http: //www. pa. msu. edu/courses/phy 231

Succeeding in Physics 231 1) Do your homework (yourself)! 2) Use the help room (1248 BPS) ! 3) Make sure you understand both “why” and “why not” 4) Interrupt the lecturer!

General Physics • First Semester (Phy 231) • Mechanics • Thermodynamics • Simple harmonic motion • Waves Second Semester (Phy 232) • Electromagnetism • Relativity • Modern Physics • (Quantum Mechanics, …, etc. )

Mechanics • Half the course • Quantified largely by Galileo • Problems involve: velocity, acceleration, mass, momentum, energy, torque, angular momentum, moment of inertia…

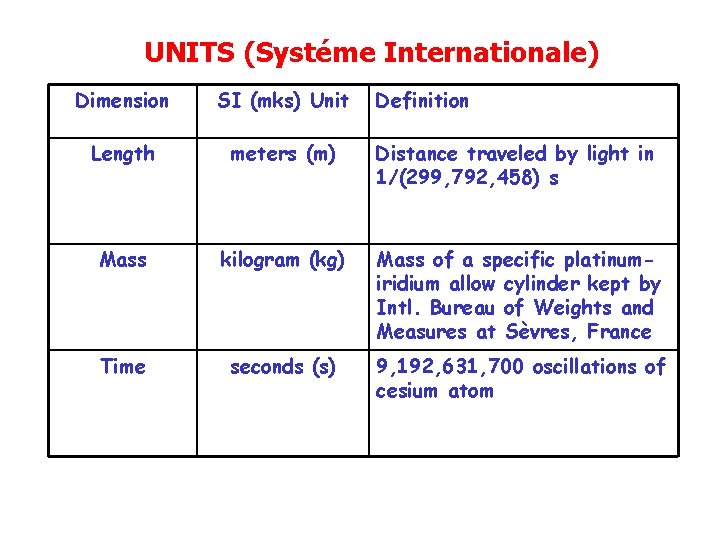
UNITS (Systéme Internationale) Dimension SI (mks) Unit Definition Length meters (m) Distance traveled by light in 1/(299, 792, 458) s Mass kilogram (kg) Mass of a specific platinumiridium allow cylinder kept by Intl. Bureau of Weights and Measures at Sèvres, France Time seconds (s) 9, 192, 631, 700 oscillations of cesium atom

Standard Kilogram at Sèvres

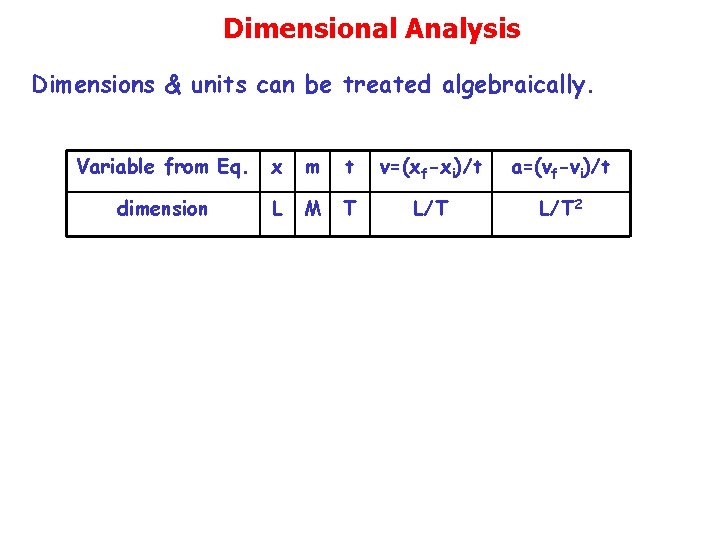
Dimensional Analysis Dimensions & units can be treated algebraically. Variable from Eq. x m t v=(xf-xi)/t a=(vf-vi)/t dimension L M T L/T 2

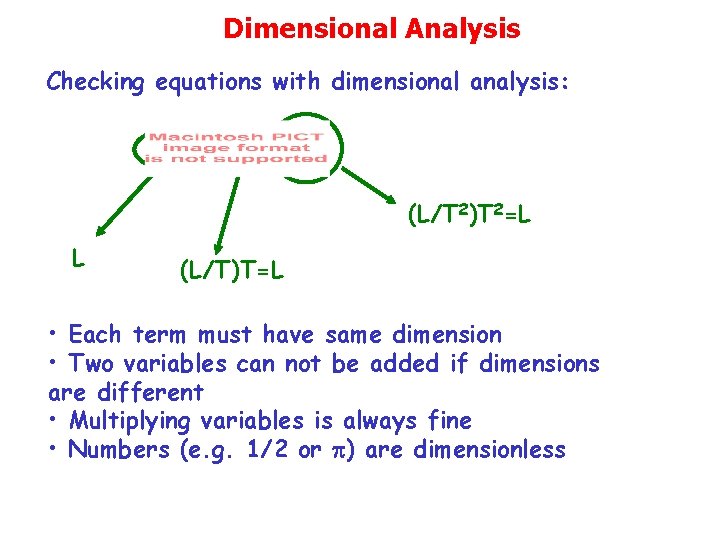
Dimensional Analysis Checking equations with dimensional analysis: (L/T 2)T 2=L L (L/T)T=L • Each term must have same dimension • Two variables can not be added if dimensions are different • Multiplying variables is always fine • Numbers (e. g. 1/2 or p) are dimensionless

Example 1. 1 Check the equation for dimensional consistency: Here, m is a mass, g is an acceleration, c is a velocity, h is a length

Example 1. 2 Consider the equation: Where m and M are masses, r is a radius and v is a velocity. What are the dimensions of G ? L 3/(MT 2)

Example 1. 3 Given “x” has dimensions of distance, “u” has dimensions of velocity, “m” has dimensions of mass and “g” has dimensions of acceleration. Is this equation dimensionally valid? Yes Is this equation dimensionally valid? No

Units vs. Dimensions: L, T, M, L/T … Units: m, mm, cm, kg, g, mg, s, hr, years … When equation is all algebra: check dimensions When numbers are inserted: check units Units obey same rules as dimensions: Never add terms with different units • Angles are dimensionless but have units (degrees or radians) • In physics sin(Y) or cos(Y) never occur unless Y is dimensionless • • •

Example 1. 3 Grandma traveled 27 minutes at 44 m/s. How many miles did Grandma travel? 44. 3 miles

Prefixes In addition to mks units, standard prefixes can be used, e. g. , cm, mm, nm

Example 1. 4 a The above expression yields: a) b) c) d) 40. 11 m 4011 cm A or B Impossible to evaluate (dimensionally invalid)

Example 1. 4 b The above expression yields: a) b) c) d) 4. 5 m kg 4. 5 g km A or B Impossible to evaluate (dimensionally invalid)

Example 1. 4 b The above expression yields: a) b) c) d) -1. 5 m -1. 5 kg m 2 -1. 5 kg Impossible to evaluate (dimensionally invalid)