PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 3 Announcement

PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 3

Announcement • HW 2 due: Wednesday Jan 23 @ 3: 59 am • (MLK Jr. Day on Jan 21) • Note: related reading for each lecture listed on Calendar page at PHY 231 website

Main points of last lecture • Acceleration defined: • Equations with constant Acceleration: ( x, v 0, vf, a, t) • Acceleration of freefall:

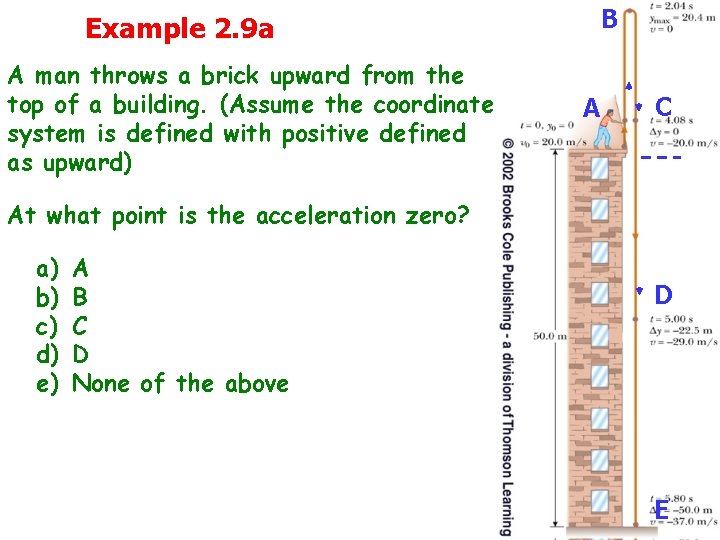
Example 2. 9 a A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positive defined as upward) B AA C C At what point is the acceleration zero? a) b) c) d) e) A B C D None of the above D D E

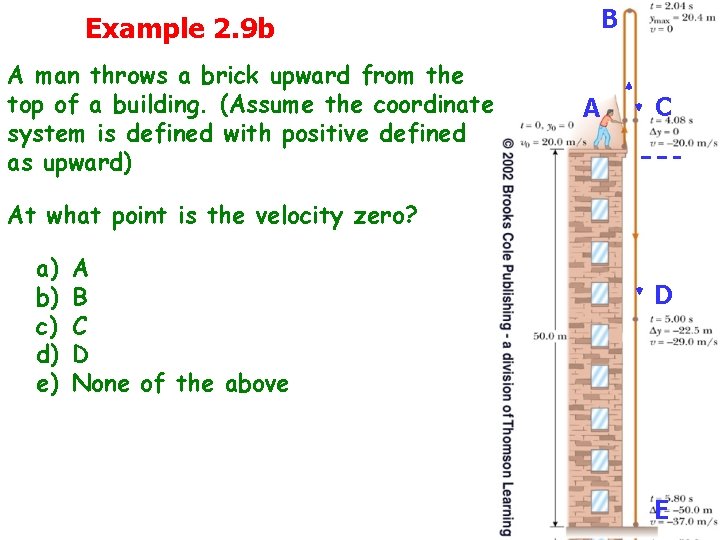
Example 2. 9 b A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positive defined as upward) B AA C C At what point is the velocity zero? a) b) c) d) e) A B C D None of the above D D E

CHAPTER 3 Two-Dimensional Motion and Vectors

Scalars and Vectors • Scalars: Magnitude only • Examples: time, distance, speed, … • Vectors: Magnitude and Direction • Examples: displacement, velocity, acceleration, …

Vectors in 2 Dimensions Vector distinguished by arrow overhead: A (x, y) y Representations: (x, y) (r, q) Cartesian Polar x

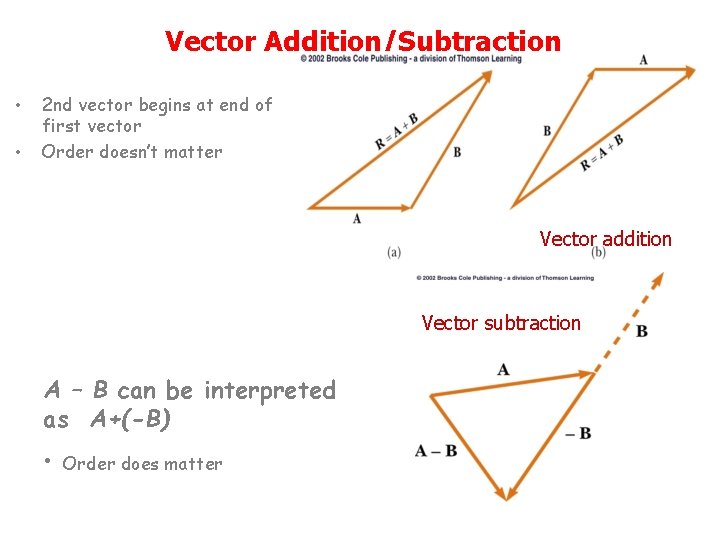
Vector Addition/Subtraction • • 2 nd vector begins at end of first vector Order doesn’t matter Vector addition Vector subtraction A – B can be interpreted as A+(-B) • Order does matter

Vector Components Cartesian components are projections along the xand y-axes Going backwards,

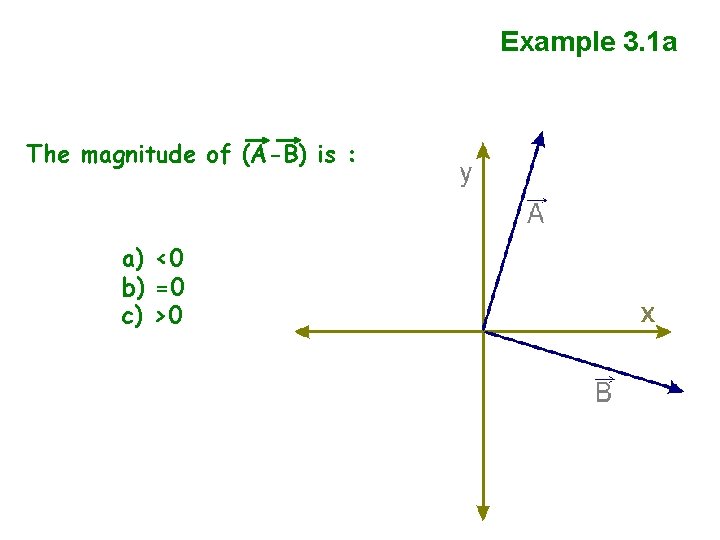
Example 3. 1 a The magnitude of (A-B) is : a) <0 b) =0 c) >0

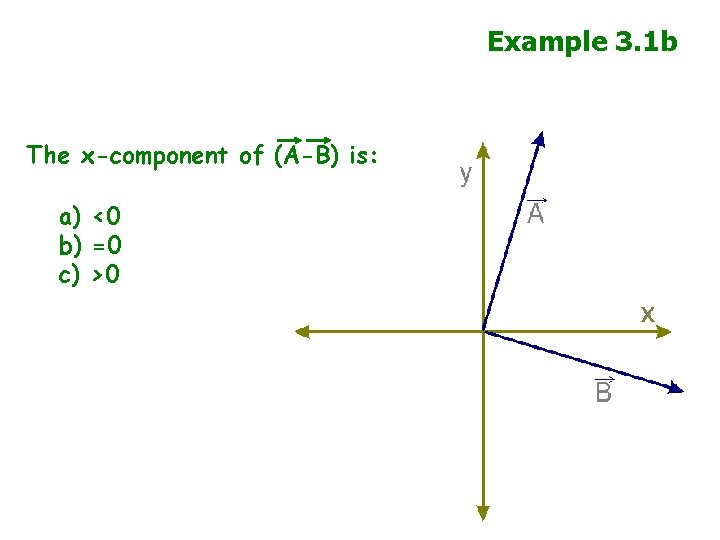
Example 3. 1 b The x-component of (A-B) is: a) <0 b) =0 c) >0

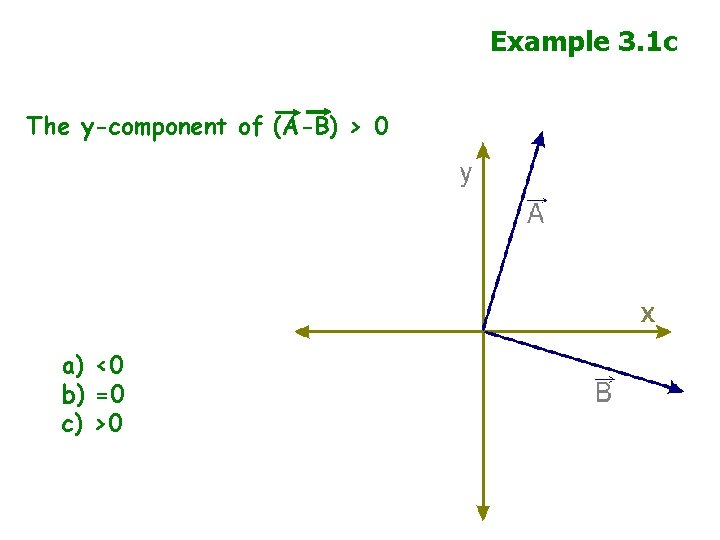
Example 3. 1 c The y-component of (A-B) > 0 a) <0 b) =0 c) >0

Example 3. 2 Some hikers walk due east from the trail head for 5 miles. Then the trail turns sharply to the southwest, and they continue for 2 more miles until they reach a waterfalls. What is the magnitude and direction of the displacement from the start of the trail to the waterfalls? 5 mi 2 mi 3. 85 miles, at -21. 5 degrees

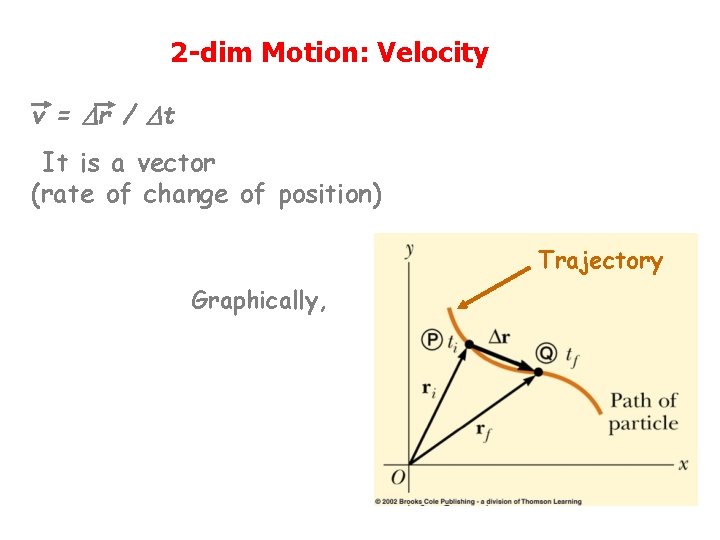
2 -dim Motion: Velocity v = Dr / Dt It is a vector (rate of change of position) Trajectory Graphically,

Multiplying/Dividing Vectors by Scalars • Example: v = Dr / Dt • Vector multiplied by scalar is a vector: B = 2 A • Magnitude changes proportionately: |B| = 2|A| • Direction is unchanged: B = A B A

2 -d Motion with constant acceleration • X- and Y-motion are independent • Two separate 1 -d problems: • • x, vx, ax y, vy, ay • Connected by time t • Important special case: Projectile motion • ax=0 • ay=-g

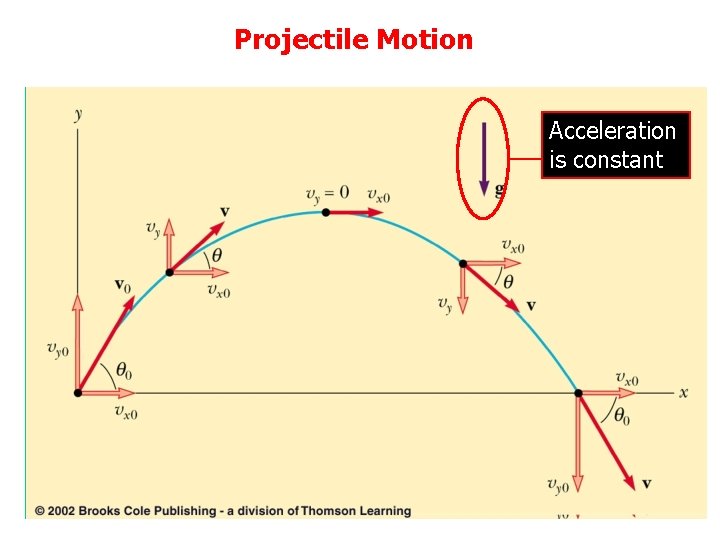
Projectile Motion • X-direction: (ax=0) • Y-direction: (ay=-g) Note: we ignore • air resistance • rotation of earth

Projectile Motion Acceleration is constant

Pop and Drop Demo The Ballistic Cart Demo

1. Write down x(t) Finding Trajectory, y(x) 2. Write down y(t) 3. Invert x(t) to find t(x) 4. Insert t(x) into y(t) to get y(x) Trajectory is parabolic

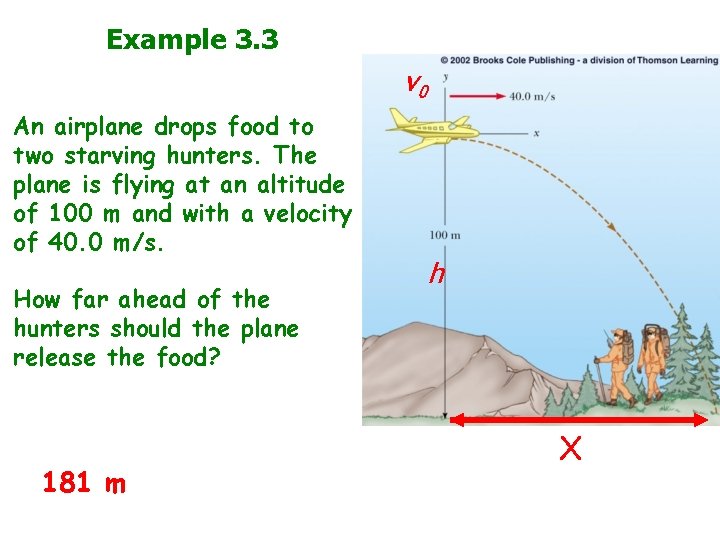
Example 3. 3 v 0 An airplane drops food to two starving hunters. The plane is flying at an altitude of 100 m and with a velocity of 40. 0 m/s. How far ahead of the hunters should the plane release the food? 181 m h X

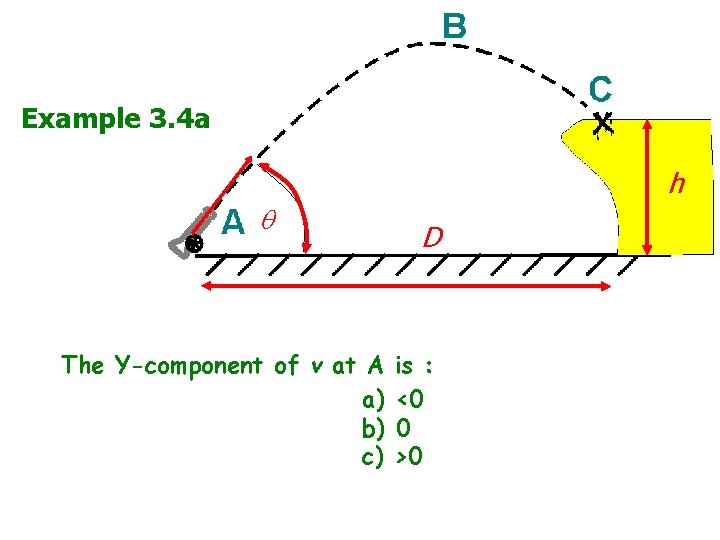
Example 3. 4 a v 0 The Y-component of v at A a) b) c) h D is : <0 0 >0

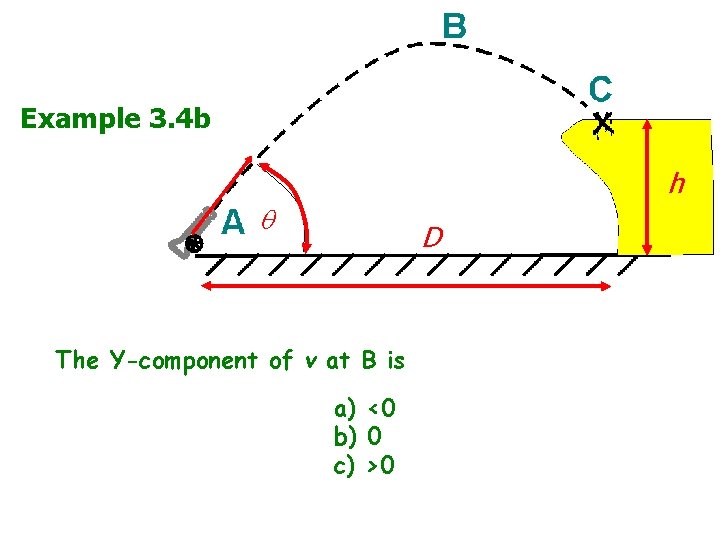
Example 3. 4 b v 0 h D The Y-component of v at B is a) <0 b) 0 c) >0

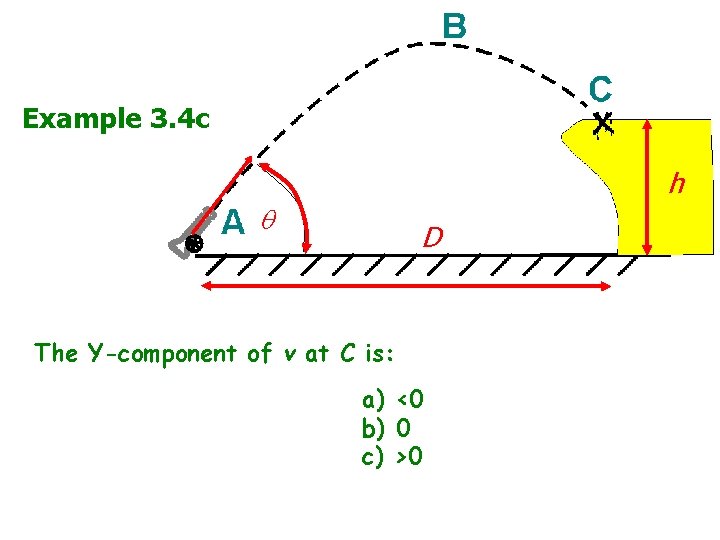
Example 3. 4 c v 0 h D The Y-component of v at C is: a) <0 b) 0 c) >0

Example 3. 4 d v 0 h D The speed is greatest at: a) b) c) d) A B C Equal at all points

Example 3. 4 e v 0 h D The X-component of v is greatest at: a) b) c) d) A B C Equal at all points

Example 3. 4 f v 0 h D The magnitude of the acceleration is greatest at: a) b) c) d) A B C Equal at all points

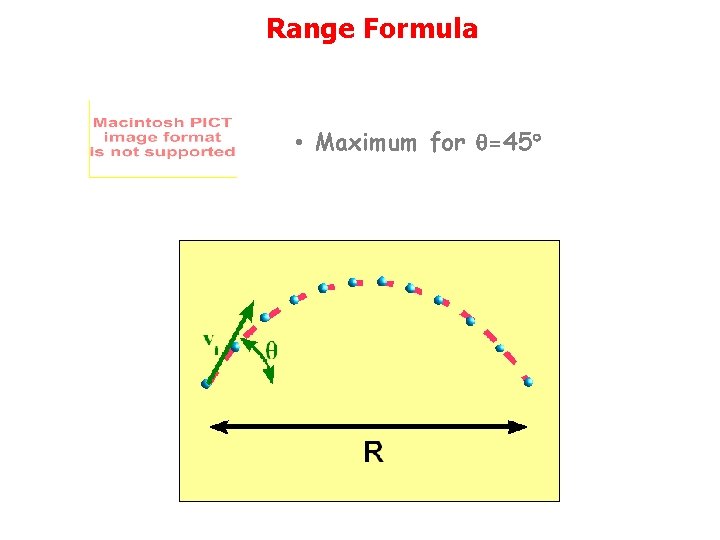
Range Formula • Good for when yf = yi

Range Formula • Maximum for q=45

Example 3. 5 a A softball leaves a bat with an initial velocity of 31. 33 m/s. What is the maximum distance one could expect the ball to travel? 100 m

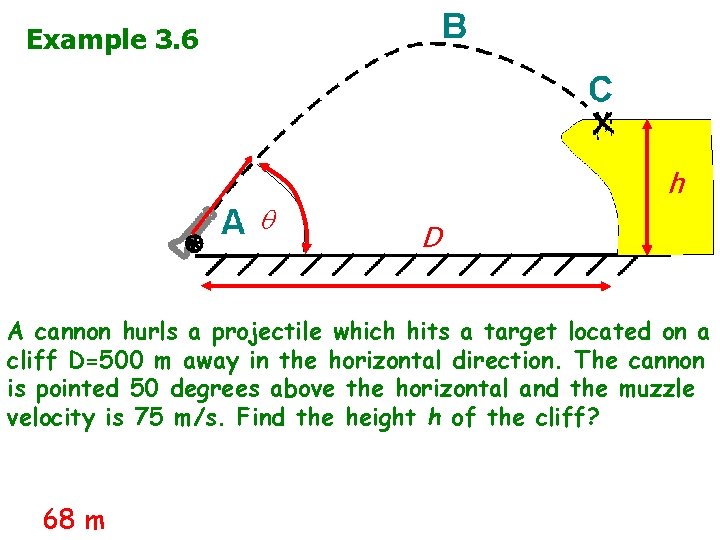
Example 3. 6 v 0 h D A cannon hurls a projectile which hits a target located on a cliff D=500 m away in the horizontal direction. The cannon is pointed 50 degrees above the horizontal and the muzzle velocity is 75 m/s. Find the height h of the cliff? 68 m