PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 20 Last

PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 20

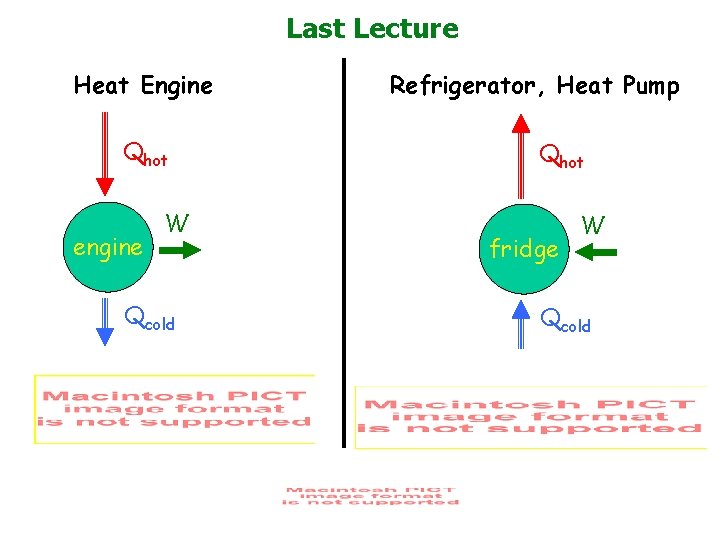
Last Lecture Heat Engine Qhot engine W Qcold Refrigerator, Heat Pump Qhot fridge W Qcold

Entropy • Measure of Disorder of the system (randomness, ignorance) • Entropy: S = k. Blog(N) N = # of possible arrangements for fixed E and Q Number of ways for 12 molecules to arrange themselves in two halves of container. S is greater if molecules spread evenly in both halves.

2 nd Law of Thermodynamics (version 2) The Total Entropy of the Universe can never decrease. (but entropy of system can increase or decrease) On a macroscopic level, one finds that adding heat raises entropy: Temperature in Kelvin!

Why does Q flow from hot to cold? • Consider two systems, one with TA and one with TB • Allow Q > 0 to flow from TA to TB • Entropy changes by: DS = Q/TB - Q/TA • This can only occur if DS > 0, requiring TA > TB. • System will achieve more randomness by exchanging heat until TB = TA

Carnot Engine Carnot cycle is most efficient possible, because the total entropy change is zero. It is a “reversible process”. For real engines:

Chapter 13 Vibrations and Waves

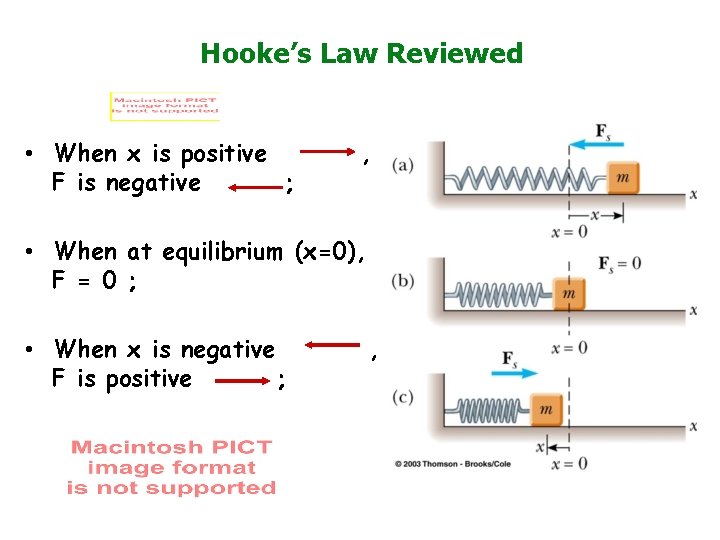
Hooke’s Law Reviewed • When x is positive F is negative ; , • When at equilibrium (x=0), F = 0 ; • When x is negative F is positive ; ,

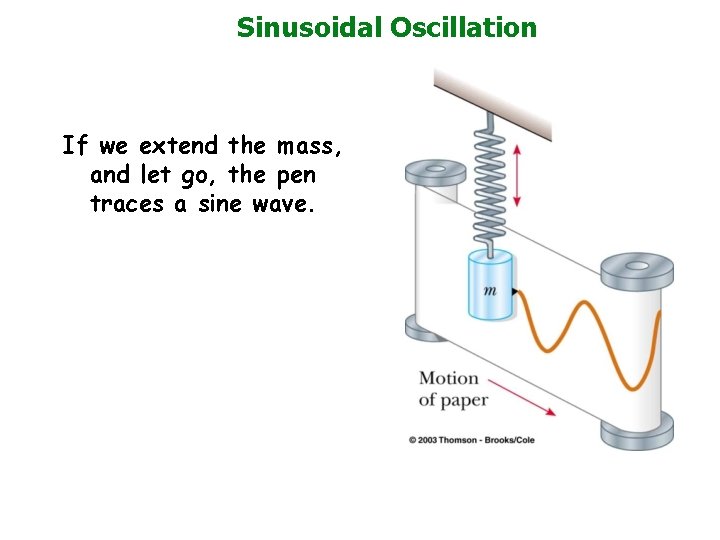
Sinusoidal Oscillation If we extend the mass, and let go, the pen traces a sine wave.

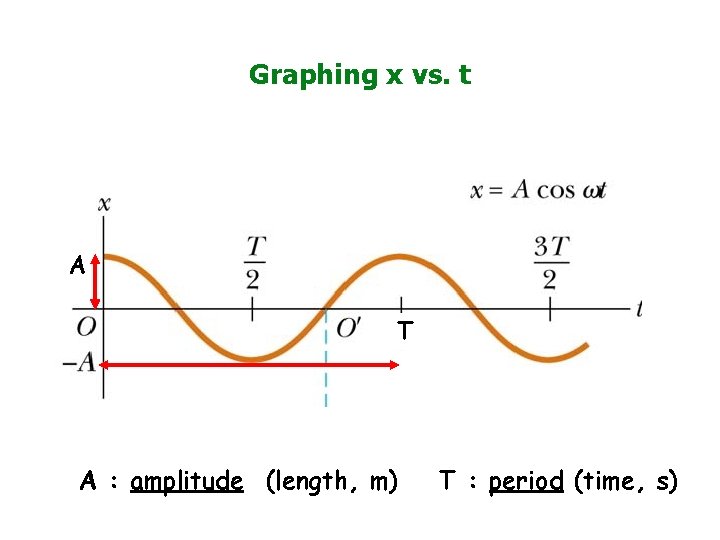
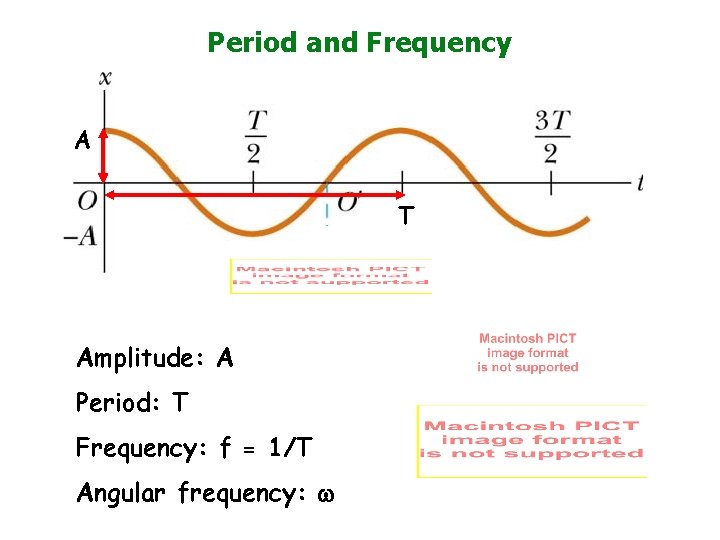
Graphing x vs. t A T A : amplitude (length, m) T : period (time, s)

Period and Frequency A T Amplitude: A Period: T Frequency: f = 1/T Angular frequency:

Phases Often a phase the peak: is included to shift the timing of for peak at Phase of 90 -degrees changes cosine to sine

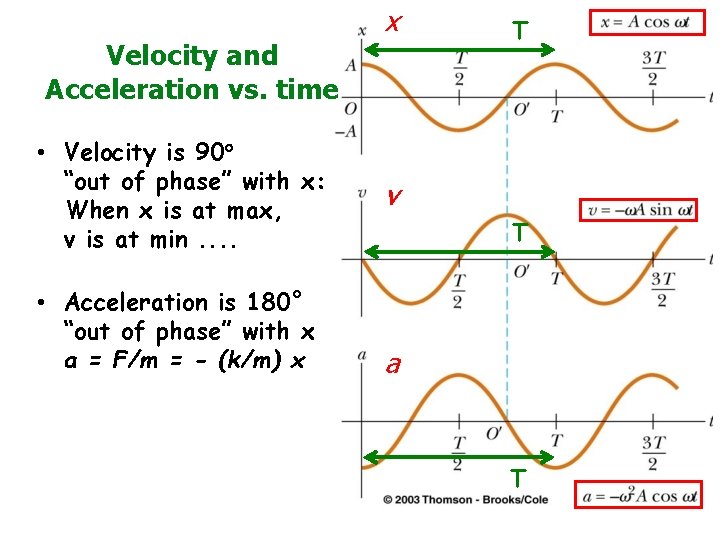
Velocity and Acceleration vs. time • Velocity is 90° “out of phase” with x: When x is at max, v is at min. . • Acceleration is 180° “out of phase” with x a = F/m = - (k/m) x x T v T a T

v and a vs. t Find vmax with E conservation Find amax using F=ma

Connection to Circular Motion Projection on axis circular motion with constant angular velocity Simple Harmonic Motion

What is ? Circular motion Simple Harmonic Motion Angular speed: Radius: A Cons. of E: => Speed: v=A

Formula Summary

Example 13. 1 An block-spring system oscillates with an amplitude of 3. 5 cm. If the spring constant is 250 N/m and the block has a mass of 0. 50 kg, determine (a) the mechanical energy of the system (b) the maximum speed of the block (c) the maximum acceleration. a) 0. 153 J b) 0. 783 m/s c) 17. 5 m/s 2

Example 13. 2 A 36 -kg block is attached to a spring of constant k=600 N/m. The block is pulled 3. 5 cm away from its equilibrium positions and released from rest at t=0. At t=0. 75 seconds, a) what is the position of the block? b) what is the velocity of the block? a) -3. 489 cm b) -1. 138 cm/s

Example 13. 3 A 36 -kg block is attached to a spring of constant k=600 N/m. The block is pulled 3. 5 cm away from its equilibrium position and is pushed so that is has an initial velocity of 5. 0 cm/s at t=0. a) What is the position of the block at t=0. 75 seconds? a) -3. 39 cm

Example 13. 4 a An object undergoing simple harmonic motion follows the expression, Where x will be in cm if t is in seconds The amplitude of the motion is: a) 1 cm b) 2 cm c) 3 cm d) 4 cm e) -4 cm

Example 13. 4 b An object undergoing simple harmonic motion follows the expression, Here, x will be in cm if t is in seconds The period of the motion is: a) 1/3 s b) 1/2 s c) 1 s d) 2 s e) 2/ s

Example 13. 4 c An object undergoing simple harmonic motion follows the expression, Here, x will be in cm if t is in seconds The frequency of the motion is: a) 1/3 Hz b) 1/2 Hz c) 1 Hz d) 2 Hz e) Hz

Example 13. 4 d An object undergoing simple harmonic motion follows the expression, Here, x will be in cm if t is in seconds The angular frequency of the motion is: a) 1/3 rad/s b) 1/2 rad/s c) 1 rad/s d) 2 rad/s e) rad/s

Example 13. 4 e An object undergoing simple harmonic motion follows the expression, Here, x will be in cm if t is in seconds The object will pass through the equilibrium position at the times, t = _____ seconds a) b) c) d) e) …, …, …, -2, -1, 0, 1, 2 … -1. 5, -0. 5, 1. 5, 2. 5, … -1. 5, -1, -0. 5, 0, 0. 5, 1. 0, 1. 5, … -4, -2, 0, 2, 4, … -2. 5, -0. 5, 1. 5, 3. 5,