PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 2 PHYSICS

PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 2

PHYSICS 231 INTRODUCTORY PHYSICS I • Lecturer: Carl Schmidt (Sec. 001) • schmidt@pa. msu. edu • (517) 355 -9200, ext. 2128 • Office Hours: Friday 1 -2: 30 pm in 1248 BPS or by appointment

Main points of last lecture • SI units: • • • Mass: kilograms (kg) Length: meters (m) Time: seconds (s) • • • Unit conversion Dimensional analysis / Unit consistency Scientific Notation and Significant figures • Displacement: x = xf-xi • Average Velocity:

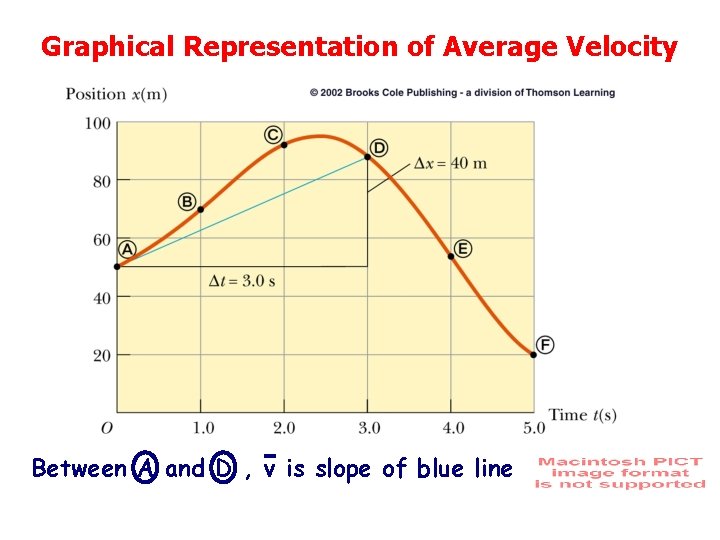
Graphical Representation of Average Velocity Between A and D , v is slope of blue line

Instantaneous velocity Let time interval approach zero • Defined for every instance in time • Equals average velocity if v = constant • SPEED is absolute value of velocity

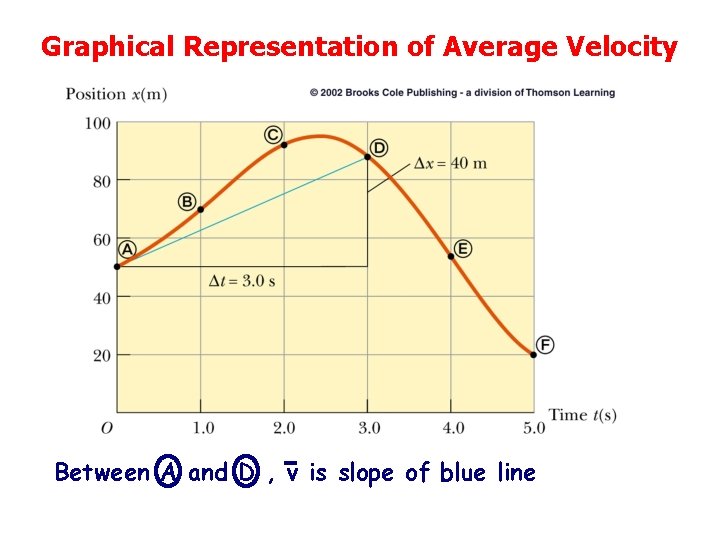
Graphical Representation of Average Velocity Between A and D , v is slope of blue line

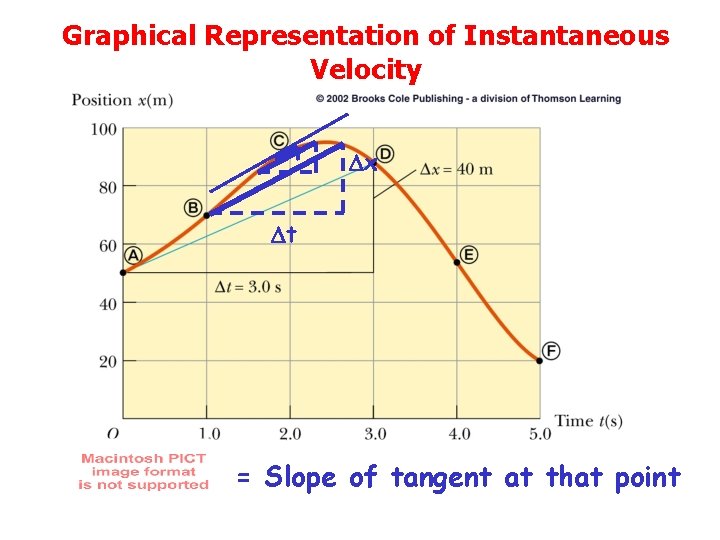
Graphical Representation of Instantaneous Velocity x t = Slope of tangent at that point

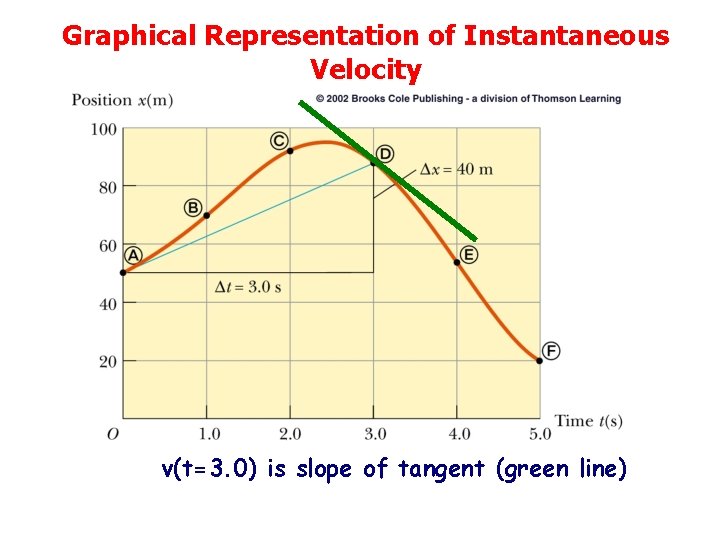
Graphical Representation of Instantaneous Velocity v(t=3. 0) is slope of tangent (green line)

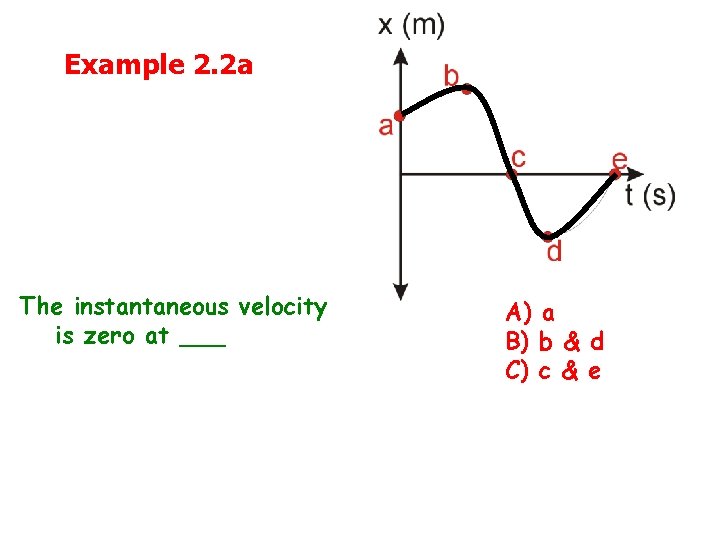
Example 2. 2 a The instantaneous velocity is zero at ___ A) a B) b & d C) c & e

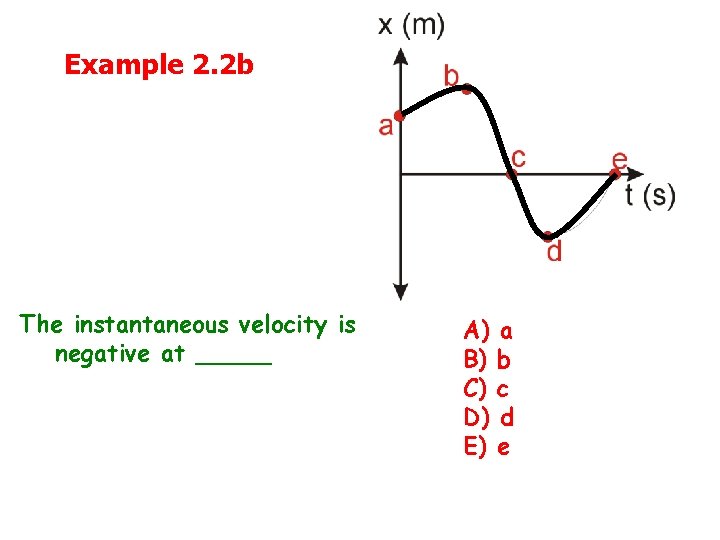
Example 2. 2 b The instantaneous velocity is negative at _____ A) B) C) D) E) a b c d e

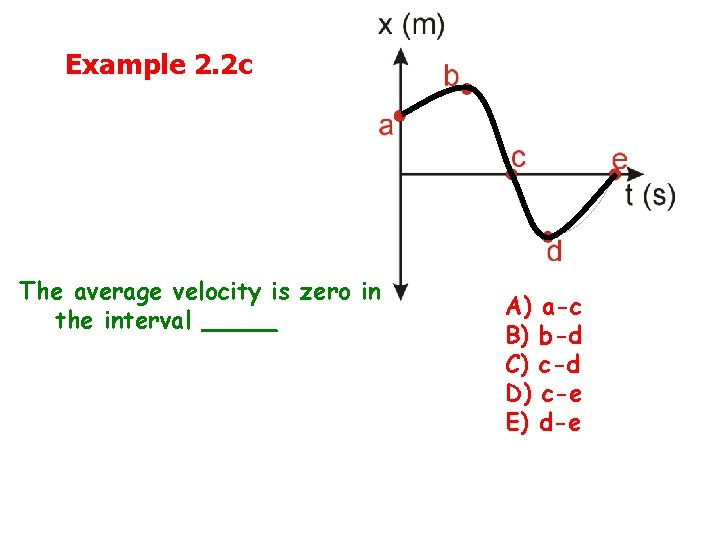
Example 2. 2 c The average velocity is zero in the interval _____ A) B) C) D) E) a-c b-d c-e d-e

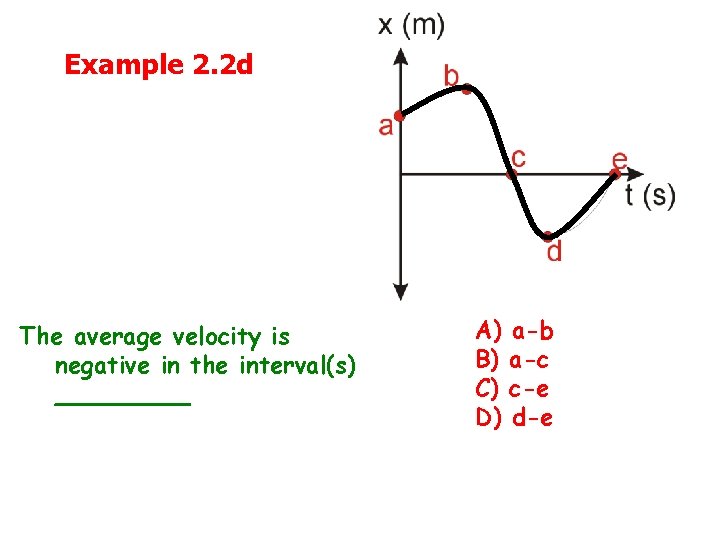
Example 2. 2 d The average velocity is negative in the interval(s) _____ A) B) C) D) a-b a-c c-e d-e

SPEED • Speed is |v| and is always positive • Average speed is sum over | x| elements divided by elapsed time

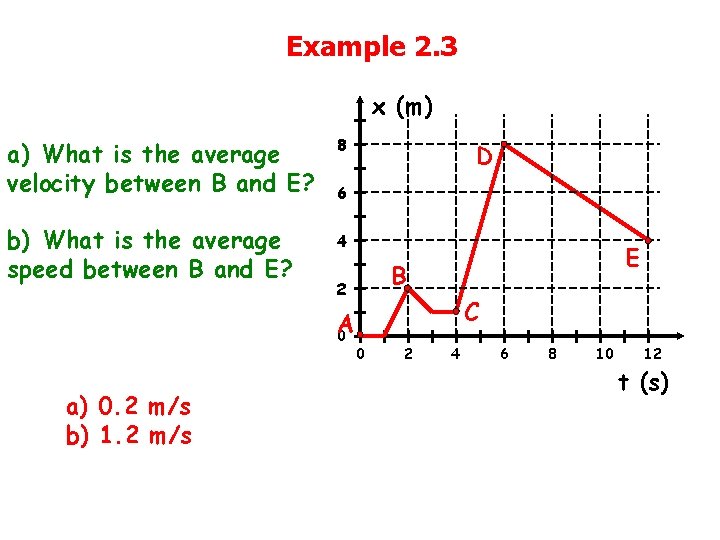
Example 2. 3 x (m) a) What is the average velocity between B and E? 8 b) What is the average speed between B and E? 4 6 E B 2 A 0 a) 0. 2 m/s b) 1. 2 m/s D C 0 2 4 6 8 10 12 t (s)

Acceleration The rate of change of the velocity Average acceleration: measured over finite time interval Instantaneous acceleration: measured over infinitesimal interval, t -> 0

Accelerometer Demo

Example 2. 4 A speed boat starts from rest and reaches 3. 2 m/s in 2 s. 1. What is its average acceleration? a = 16 m/s 2 2. Assuming acceleration is constant, what is its velocity after 5 s? vf = v 0+at = 8 m/s

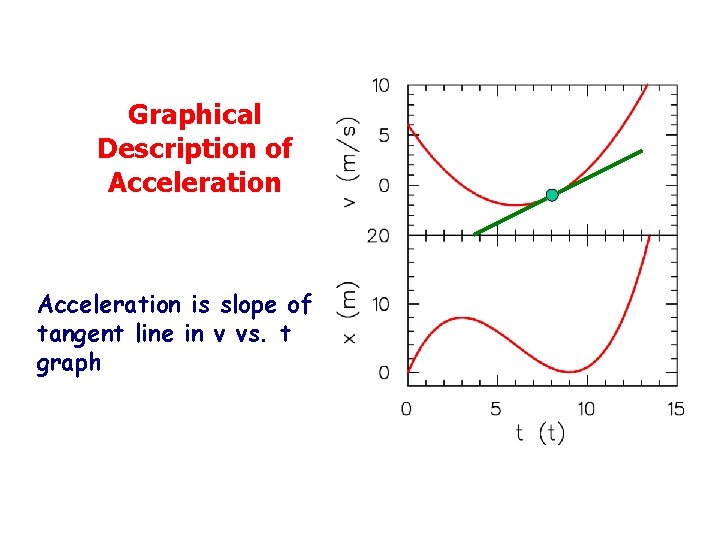
Graphical Description of Acceleration is slope of tangent line in v vs. t graph

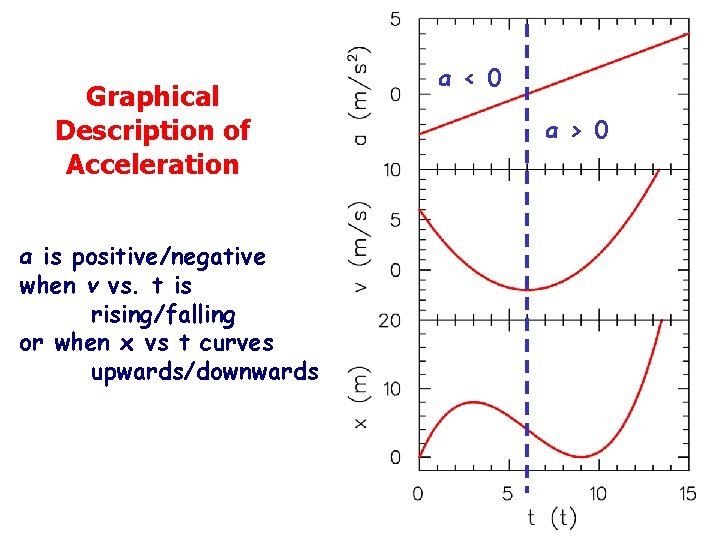
Graphical Description of Acceleration a is positive/negative when v vs. t is rising/falling or when x vs t curves upwards/downwards a < 0 a > 0

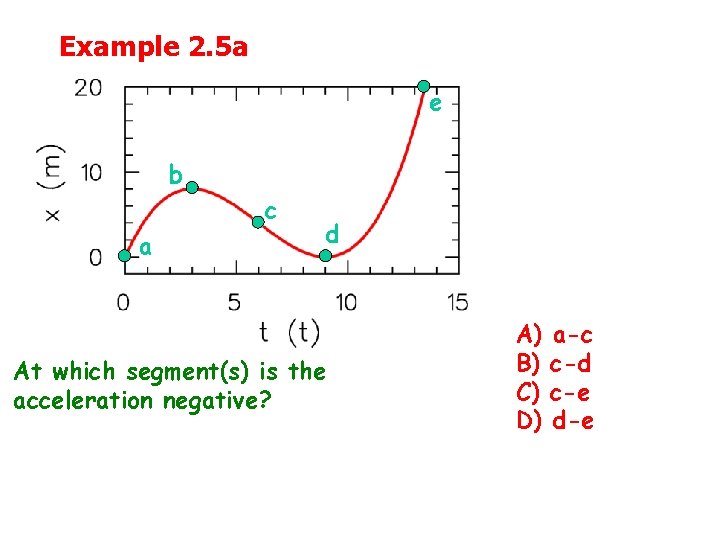
Example 2. 5 a e b c a d At which segment(s) is the acceleration negative? A) B) C) D) a-c c-d c-e d-e

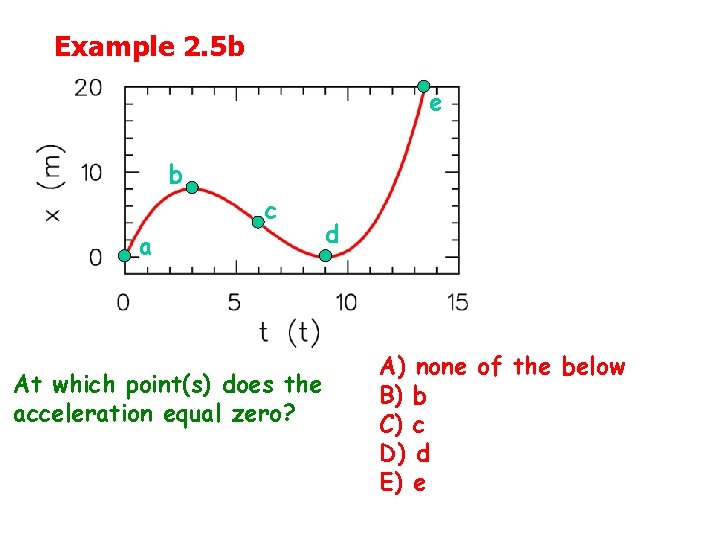
Example 2. 5 b e b c a At which point(s) does the acceleration equal zero? d A) B) C) D) E) none of the below b c d e

Constant Acceleration • Recall • v vs. t is a straight line • Also • Combining: • x vs. t is a parabola

Example 2. 6 A speed boat starts from rest and accelerates at a rate of 1. 6 m/s 2. How far does it go after 5 s? x = 20 m

Solving Problems with Eq. s of Motion 5 variables: x, t, v 0, vf, a 3 equations (so far): Must be 2 more equations

Other Forms of Eq. s of Motion Substitute to eliminate v 0

Other Forms of Eq. s of Motion Substitute to eliminate t

Final List of 1 -d Equations Which equation to use? Each has 4 of the 5 variables: Dx, t, v 0, v & a Ask yourself “Which variable am I not given and not interested in? ” If that variable is t, use Eq. (5).

Example 2. 7 Crash Houlihan speeds down the interstate at 44 m/s (100 mph), when she slams on the brakes and slides into a concrete barrier. The police measure skid marks to be 60 m long, and estimate that her Mercedes would decelerate at 11 m/s 2 while skidding. What was Crash’s speed when she hit the barrier? 25 m/s

Free Fall • Special case of constant acceleration: • Objects near Earth’s surface falling under the influence of gravity (neglecting air resistance) • Acceleration g = 9. 81 m/s 2 • Use the usual equations with (with convention up is +)

Galileo • Father was a musician, experimented with music • Initially was a professor teaching pre-meds • Developed telescope ~ 1610: Milky Way = stars Moons of Jupiter Phases of Venus… • Measured g • Quantified mechanics • In 1632, published Dialogue concerning the two greatest world systems • Was found guilty of heresy

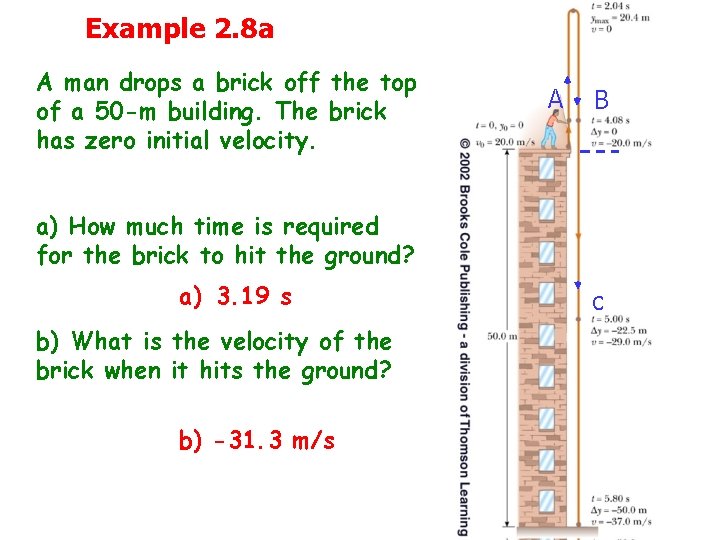
Example 2. 8 a A man drops a brick off the top of a 50 -m building. The brick has zero initial velocity. A B a) How much time is required for the brick to hit the ground? a) 3. 19 s b) What is the velocity of the brick when it hits the ground? b) -31. 3 m/s c

Example 2. 8 b A man throws a brick upward from the top of a 50 m building. The brick has an initial upward velocity of 20 m/s. A B a) How high above the building does the brick get before it falls? b) How much time does the brick spend going upwards? c) What is the velocity of the brick when it passes the man going downwards? d) What is the velocity of the brick when it hits the ground? e) At what time does the brick hit the ground? c

Example 2. 8 b A man throws a brick upward from the top of a 50 m building. The brick has an initial upward velocity of 20 m/s. a) How high above the building does the brick get before it falls? b) How much time does the brick spend going upwards? c) What is the velocity of the brick when it passes the man going downwards? d) What is the velocity of the brick when it hits the ground? e) At what time does the brick hit the ground? a) b) c) d) e) 20. 4 m 2. 04 s -20 m/s -37. 2 m/s 5. 83 s

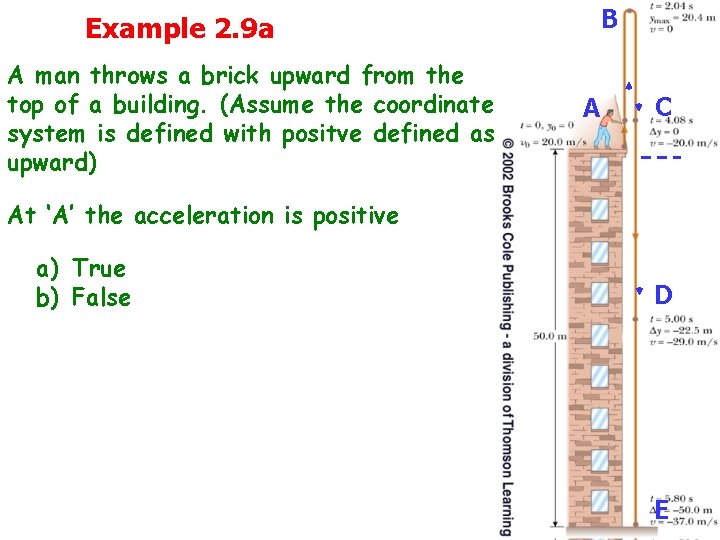
Example 2. 9 a A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positve defined as upward) B AA C C At ‘A’ the acceleration is positive a) True b) False D D E

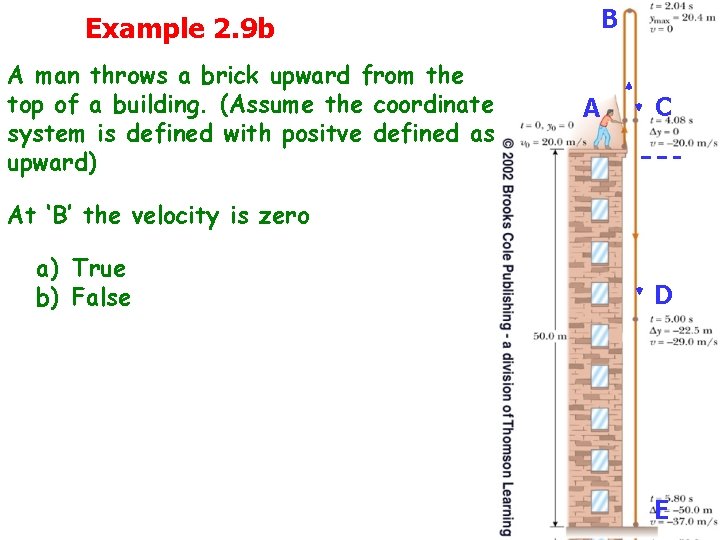
Example 2. 9 b A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positve defined as upward) B AA C C At ‘B’ the velocity is zero a) True b) False D D E

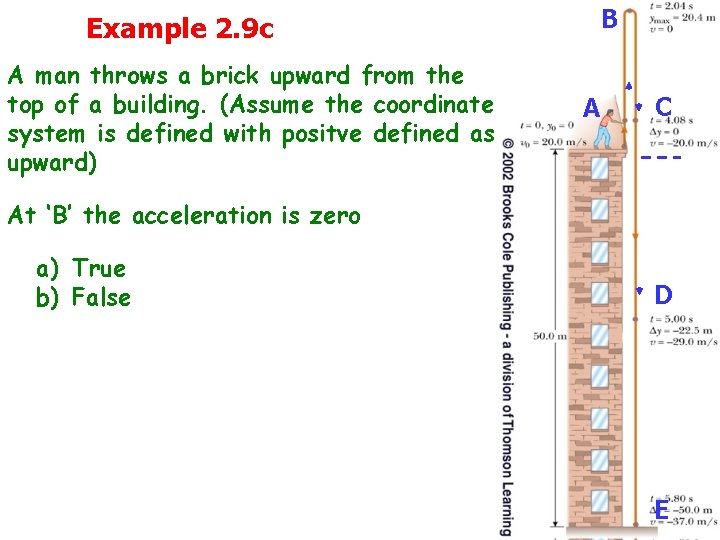
Example 2. 9 c A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positve defined as upward) B AA C C At ‘B’ the acceleration is zero a) True b) False D D E

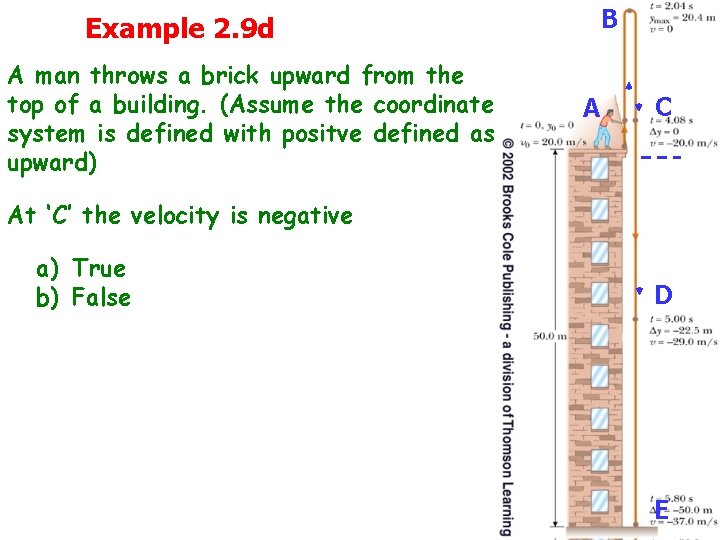
Example 2. 9 d A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positve defined as upward) B AA C C At ‘C’ the velocity is negative a) True b) False D D E

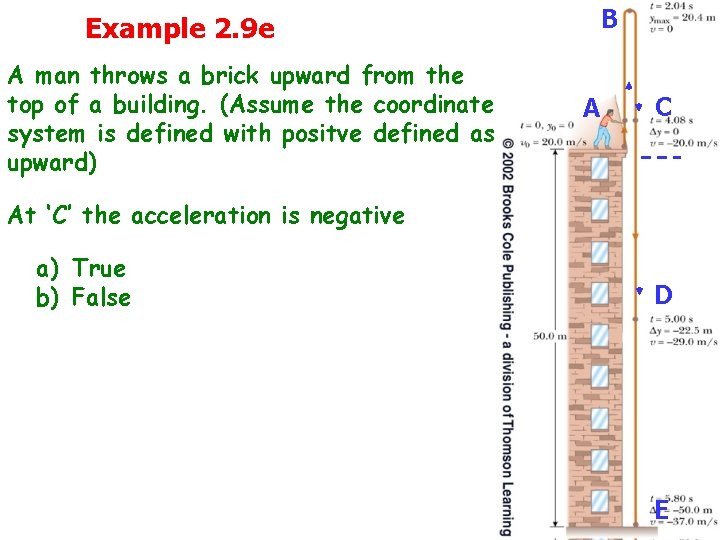
Example 2. 9 e A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positve defined as upward) B AA C C At ‘C’ the acceleration is negative a) True b) False D D E

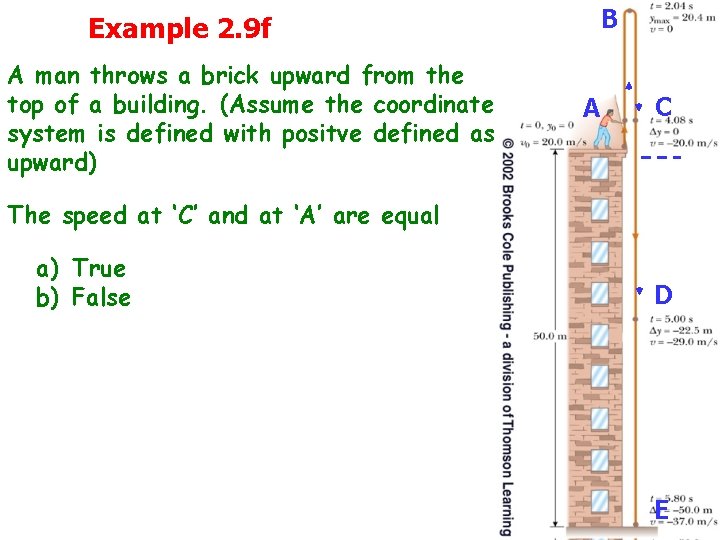
Example 2. 9 f A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positve defined as upward) B AA C C The speed at ‘C’ and at ‘A’ are equal a) True b) False D D E

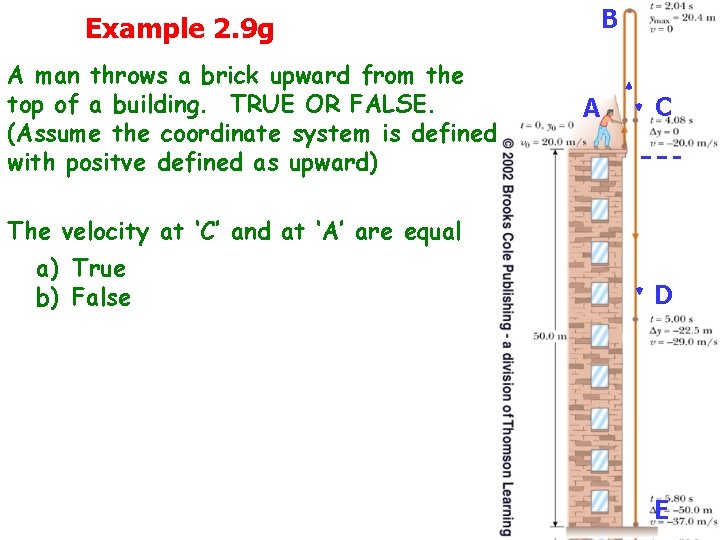
Example 2. 9 g A man throws a brick upward from the top of a building. TRUE OR FALSE. (Assume the coordinate system is defined with positve defined as upward) B AA C C The velocity at ‘C’ and at ‘A’ are equal a) True b) False D D E

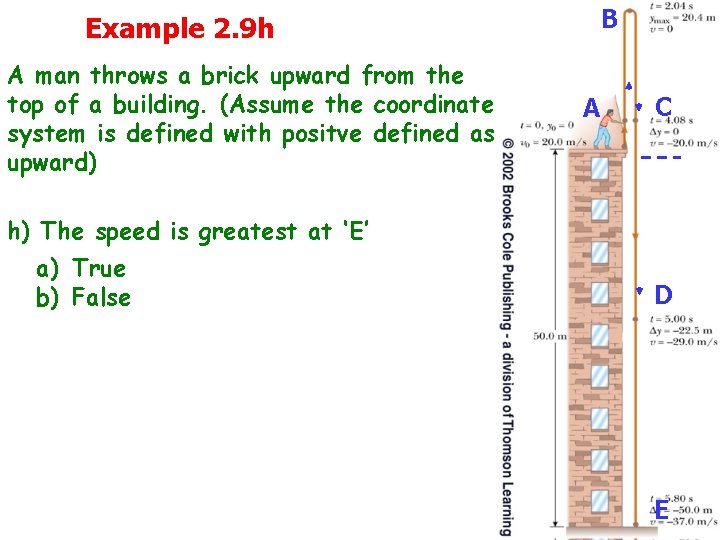
Example 2. 9 h A man throws a brick upward from the top of a building. (Assume the coordinate system is defined with positve defined as upward) B AA C C h) The speed is greatest at ‘E’ a) True b) False D D E