PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 19 Last

PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 19

Last Lecture • First Law of Thermodynamics • Work done by/on a gas

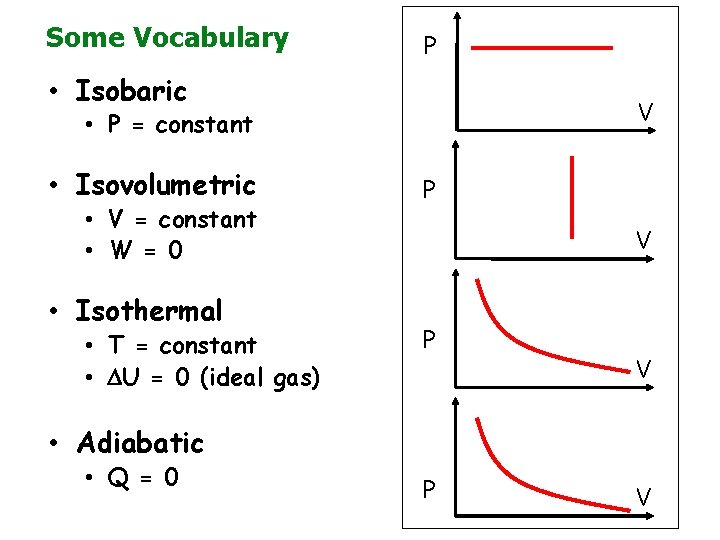
Some Vocabulary P • Isobaric V • P = constant • Isovolumetric • V = constant • W = 0 • Isothermal • T = constant • U = 0 (ideal gas) P V • Adiabatic • Q = 0 P V

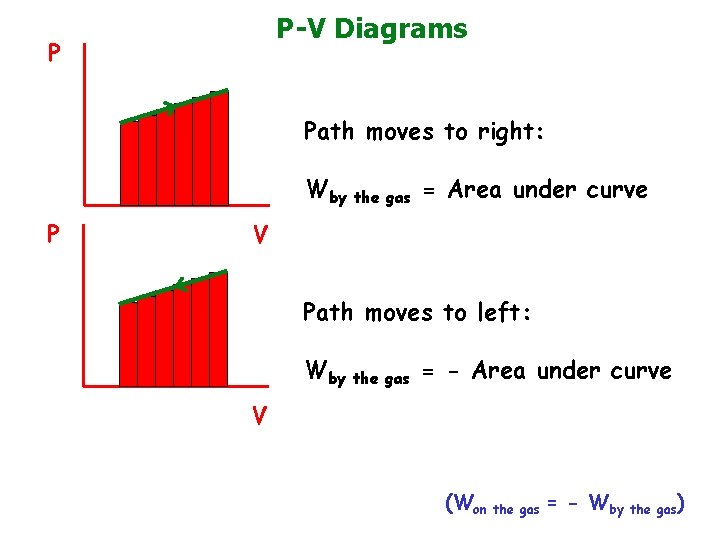
P-V Diagrams P Path moves to right: Wby the gas = Area under curve P V Path moves to left: Wby the gas = - Area under curve V (Won the gas = - Wby the gas)

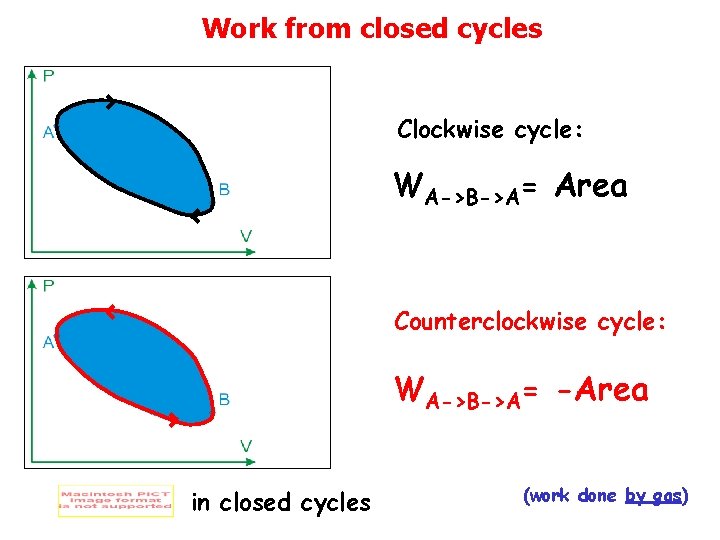
Work from closed cycles Clockwise cycle: WA->B->A= Area Counterclockwise cycle: WA->B->A= -Area in closed cycles (work done by gas)

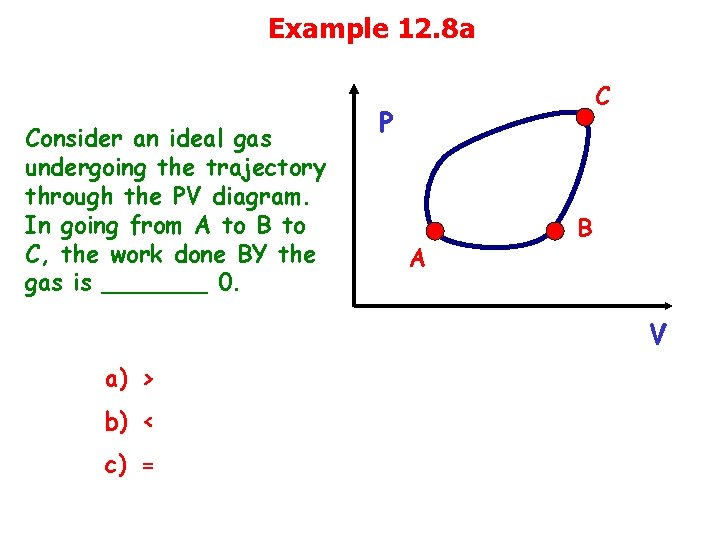
Example 12. 8 a Consider an ideal gas undergoing the trajectory through the PV diagram. In going from A to B to C, the work done BY the gas is _______ 0. C P A B V a) > b) < c) =

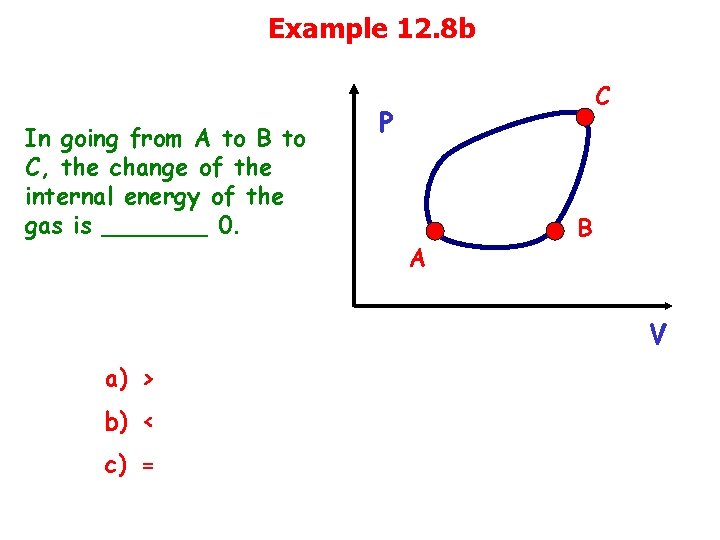
Example 12. 8 b In going from A to B to C, the change of the internal energy of the gas is _______ 0. C P A B V a) > b) < c) =

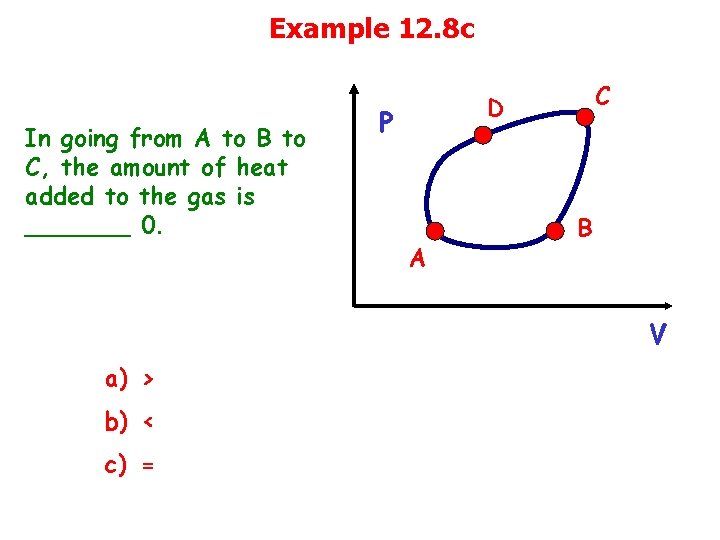
Example 12. 8 c In going from A to B to C, the amount of heat added to the gas is _______ 0. C D P A B V a) > b) < c) =

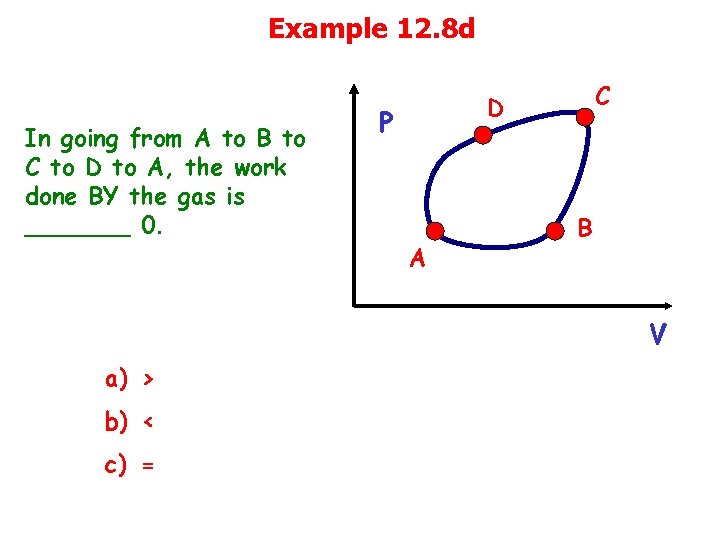
Example 12. 8 d In going from A to B to C to D to A, the work done BY the gas is _______ 0. C D P A B V a) > b) < c) =

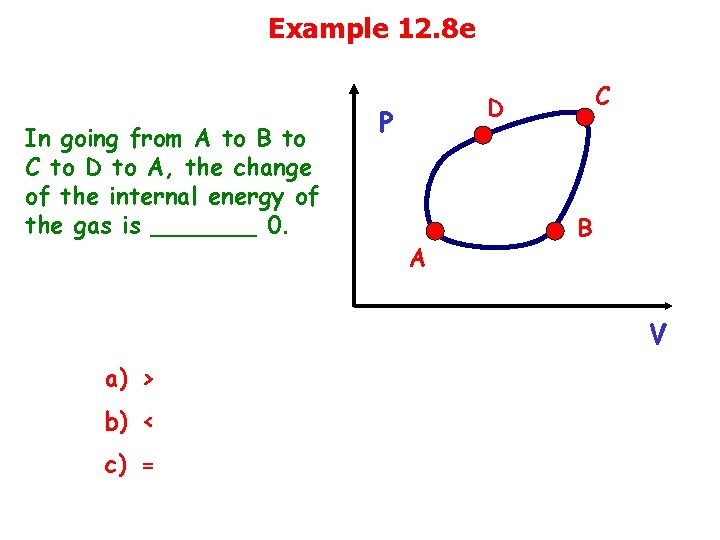
Example 12. 8 e In going from A to B to C to D to A, the change of the internal energy of the gas is _______ 0. C D P A B V a) > b) < c) =

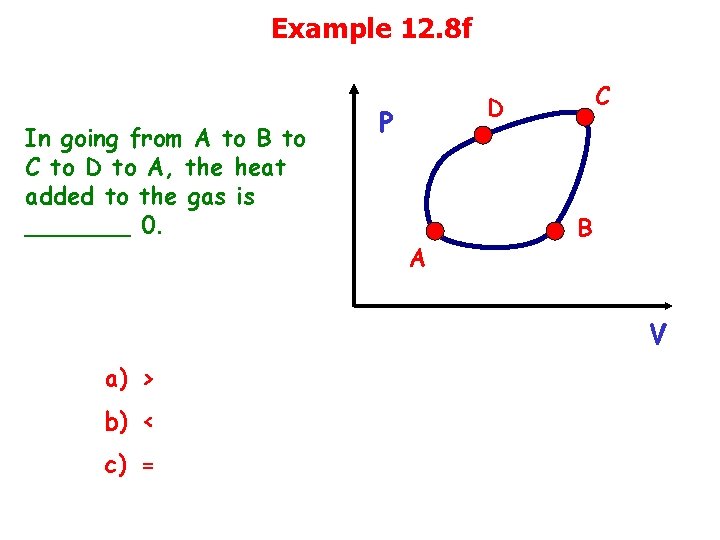
Example 12. 8 f In going from A to B to C to D to A, the heat added to the gas is _______ 0. C D P A B V a) > b) < c) =

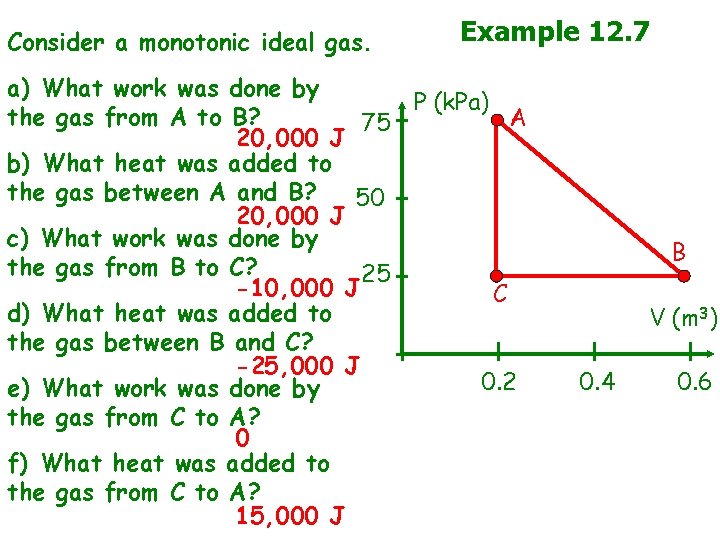
Consider a monotonic ideal gas. Example 12. 7 a) What work was done by P (k. Pa) the gas from A to B? A 75 20, 000 J b) What heat was added to the gas between A and B? 50 20, 000 J c) What work was done by the gas from B to C? 25 -10, 000 J C d) What heat was added to the gas between B and C? -25, 000 J 0. 2 e) What work was done by the gas from C to A? 0 f) What heat was added to the gas from C to A? 15, 000 J B V (m 3) 0. 4 0. 6

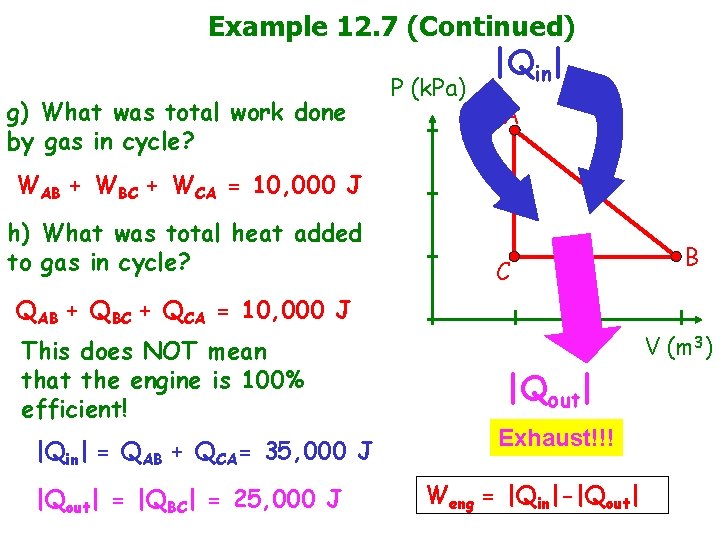
Example 12. 7 (Continued) g) What was total work done by gas in cycle? P (k. Pa) |Qin| A WAB + WBC + WCA = 10, 000 J h) What was total heat added to gas in cycle? C B QAB + QBC + QCA = 10, 000 J This does NOT mean that the engine is 100% efficient! |Qin| = QAB + QCA= 35, 000 J |Qout| = |QBC| = 25, 000 J V (m 3) |Qout| Exhaust!!! Weng = |Qin|-|Qout|

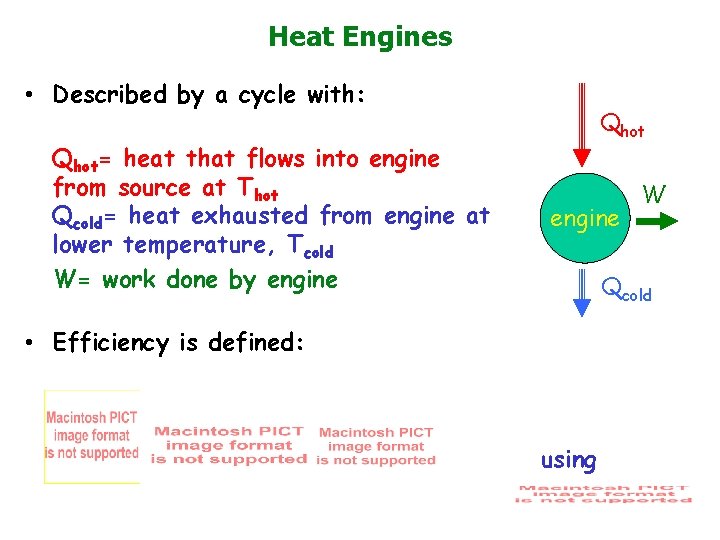
Heat Engines • Described by a cycle with: Qhot= heat that flows into engine from source at Thot Qcold= heat exhausted from engine at lower temperature, Tcold W= work done by engine Qhot engine W Qcold • Efficiency is defined: using

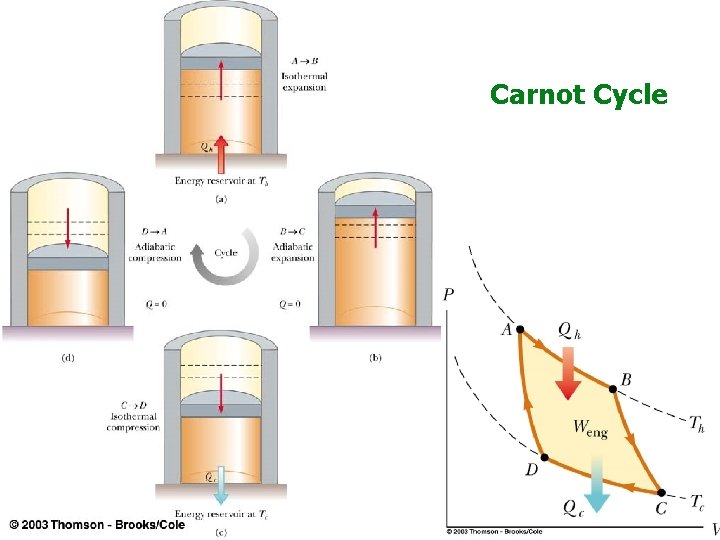
2 nd Law of Thermodynamics (version 1) No heat engine can be 100% efficient The most efficient engine is the Carnot Engine (an idealized engine), for which: (T in Kelvin) In practice, we always have

Carnot Cycle

Example 12. 9 An ideal engine (Carnot) is rated at 50% efficiency when it is able to exhaust heat at a temperature of 20 ºC. If the exhaust temperature is lowered to -30 ºC, what is the new efficiency. e = 0. 585

Refrigerators Just a heat engine run in reverse! • Pull Qcold from fridge • Exhaust Qhot to outside Coefficient of Performance: Qhot fridge W Qcold Most efficient is Carnot refrigerator: Note: Highest COP for small T differences

Heat Pumps Same as refrigerator, except • Pull Qcold from environment • Exhaust Qhot to inside of house Coefficient of Performance: Qhot heat pump W Qcold Again, most efficient is Carnot: Like Refrigerator: Best performance for small T

Example 12. 10 A modern gas furnace can work at practically 100% efficiency, i. e. , 100% of the heat from burning the gas is converted into heat for the home. Assume that a heat pump works at 50% of the efficiency of an ideal heat pump. If electricity costs 3 times as much per kw-hr as gas, for what range of outside temperatures is it advantageous to use a heat pump? Assume Tinside = 295 ºK.

Entropy • Measure of Disorder of the system (randomness, ignorance) • S = k. Blog(N) N = # of possible arrangements for fixed E and Q Relative probabilities for 12 molecules to arrange on two halves of container.

2 nd Law of Thermodynamics (version 2) The Total Entropy of the Universe can never decrease. On a macroscopic level, one finds that adding heat raises entropy: Defines temperature in Kelvin!

Why does Q flow from hot to cold? • Consider two systems, one with TA and one with TB • Allow Q > 0 to flow from TA to TB • Entropy changes by: S = Q/TB - Q/TA • This can only occur if S > 0, requiring TA > TB. • System will achieve more randomness by exchanging heat until TB = TA

Carnot Engine Carnot cycle is most efficient possible, because the total entropy change is zero. It is a “reversible process”. For real engines:

Example 12. 11 a An engine does an amount of work W, and exhausts heat at a temperature of 50 degrees C. The chemical energy contained in the fuel must be greater than, and not equal to, W. a) True b) False

Example 12. 11 b A locomotive is powered by a large engine that exhausts heat into a large heat exchanger that stays close to the temperature of the atmosphere. The engine should be more efficient on a very cold day than on a warm day. a) True b) False

Example 12. 11 c An air conditioner uses an amount of electrical energy U to cool a home. The amount of heat removed from the home must be less than or equal to U. a) True b) False

Example 12. 11 d A heat pump uses an amount of electrical energy U to heat a home. The amount of heat added to a home must be less than or equal to U. a) True b) False