PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 12 Last

PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 12

Last Lecture • Newton’s Law of gravitation • Kepler’s Laws of Planetary motion 1. Ellipses with sun at focus 2. Sweep out equal areas in equal times 3.

Gravitational Potential Energy • PE = mgh valid only near Earth’s surface • For arbitrary altitude • Zero reference level is at r=

Example 7. 18 You wish to hurl a projectile from the surface of the Earth (Re= 6. 38 x 106 m) to an altitude of 20 x 106 m above the surface of the Earth. Ignore rotation of the Earth and air resistance. a) What initial velocity is required? a) 9, 736 m/s b) What velocity would be required in order for the projectile to reach infinitely high? I. e. , what is the escape velocity? b) 11, 181 m/s c) (skip) How does the escape velocity compare to the velocity required for a low earth orbit? c) 7, 906 m/s

Chapter 8 Rotational Equilibrium and Rotational Dynamics

Wrench Demo

Torque • Torque, t , is tendency of a force to rotate object about some axis • F is the force • d is the lever arm (or moment arm) • Units are Newton-meters Door Demo

Torque is vector quantity • Direction determined by axis of twist • Perpendicular to both r and F • Clockwise torques point into paper. Defined as negative • Counter-clockwise torques point out of paper. Defined as positive r - r F + F

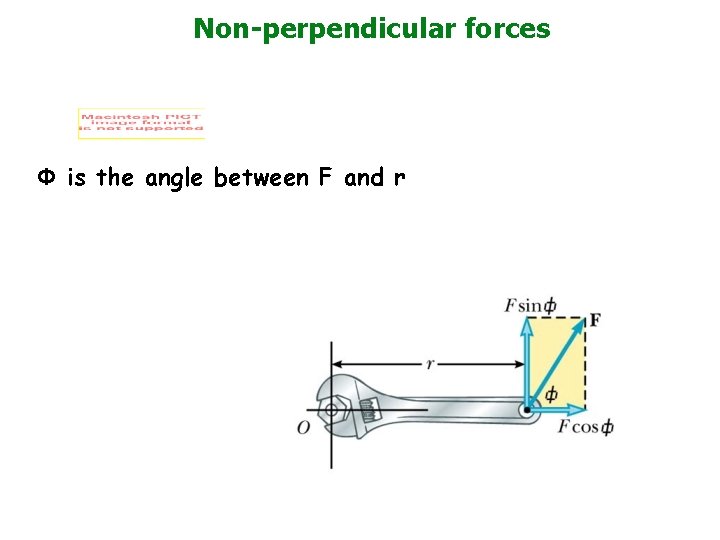
Non-perpendicular forces Φ is the angle between F and r

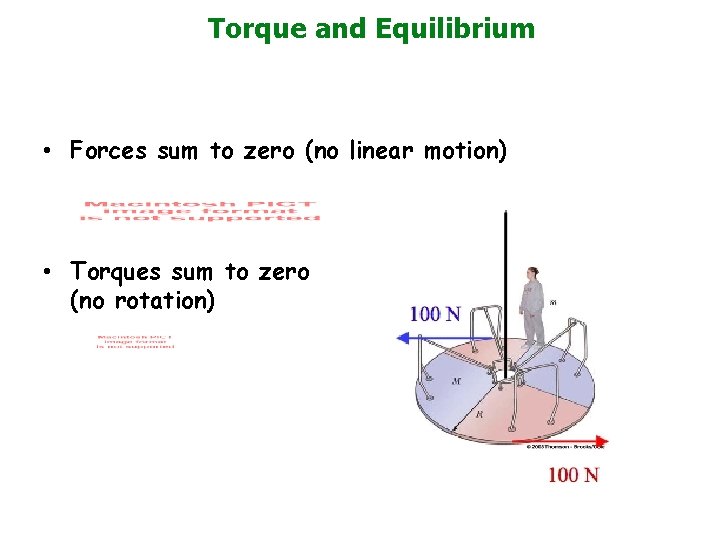
Torque and Equilibrium • Forces sum to zero (no linear motion) • Torques sum to zero (no rotation)

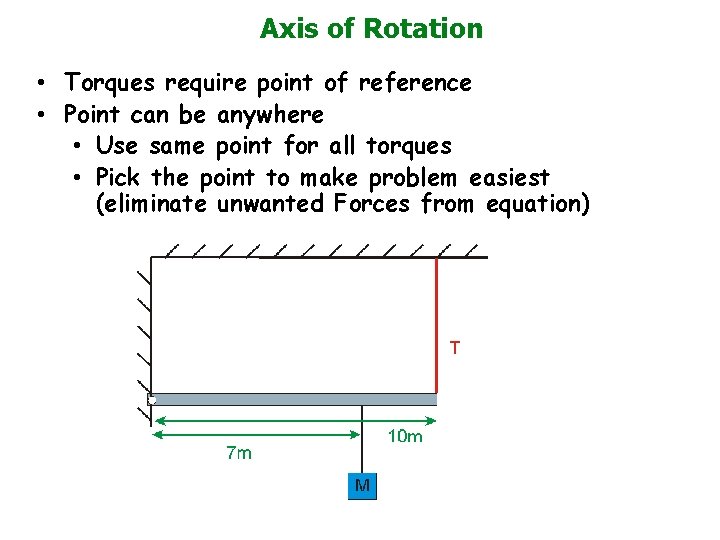
Axis of Rotation • Torques require point of reference • Point can be anywhere • Use same point for all torques • Pick the point to make problem easiest (eliminate unwanted Forces from equation)

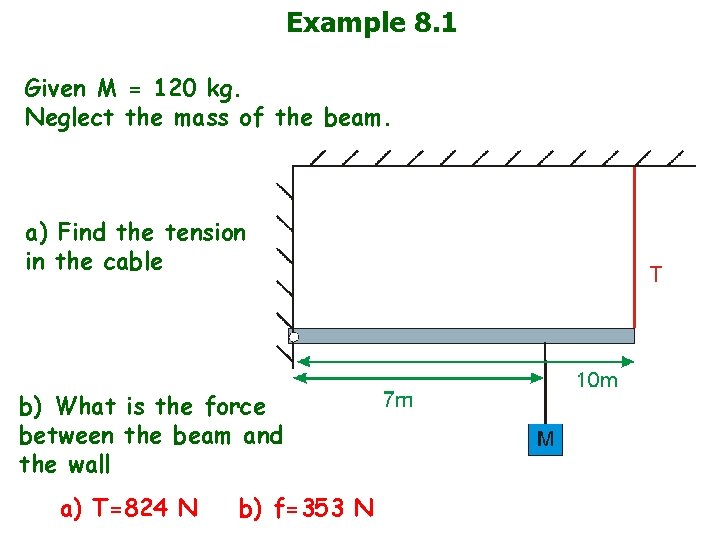
Example 8. 1 Given M = 120 kg. Neglect the mass of the beam. a) Find the tension in the cable b) What is the force between the beam and the wall a) T=824 N b) f=353 N

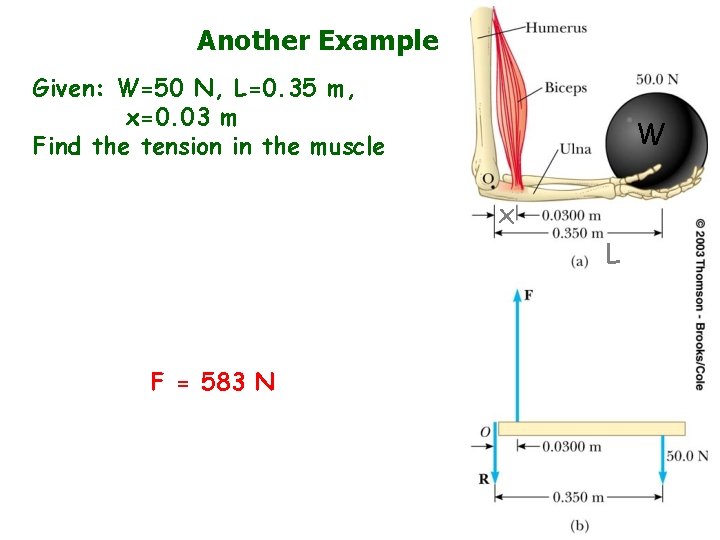
Another Example Given: W=50 N, L=0. 35 m, x=0. 03 m Find the tension in the muscle W x L F = 583 N

Center of Gravity • Gravitational force acts on all points of an extended object • However, one can treat gravity as if it acts at one point: the center-of-gravity. • Center of gravity:

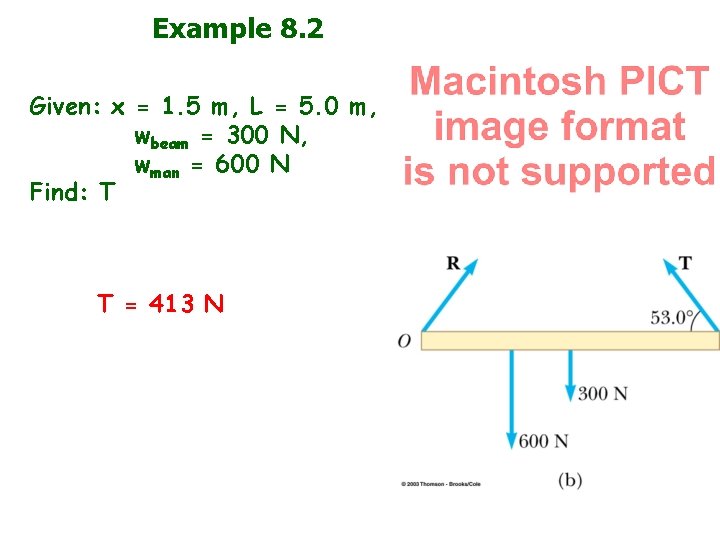
Example 8. 2 Given: x = 1. 5 m, L = 5. 0 m, wbeam = 300 N, wman = 600 N Find: T T = 413 N x L

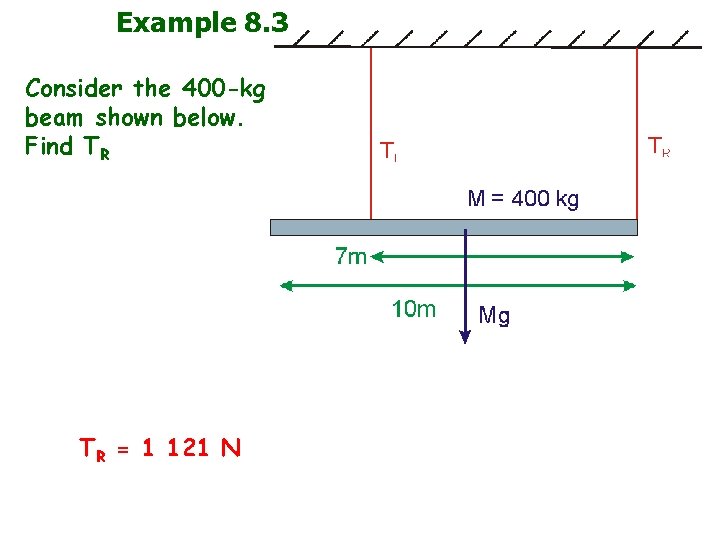
Example 8. 3 Consider the 400 -kg beam shown below. Find TR TR = 1 121 N

Example 8. 4 a Given: Wbeam=300 Wbox=200 Find: Tleft What point should I use for torque origin? A B C D

Example 8. 4 b Given: Tleft=300 Tright=500 Find: Wbeam What point should I use for torque origin? A B C D

Example 8. 4 c Given: Tleft=250 Tright=400 Find: Wbox What point should I use for torque origin? A B C D

Example 8. 4 d Given: Wbeam=300 Wbox=200 Find: Tright What point should I use for torque origin? A B C D

Example 8. 4 e Given: Tleft=250 Wbeam=250 Find: Wbox What point should I use for torque origin? A B C D

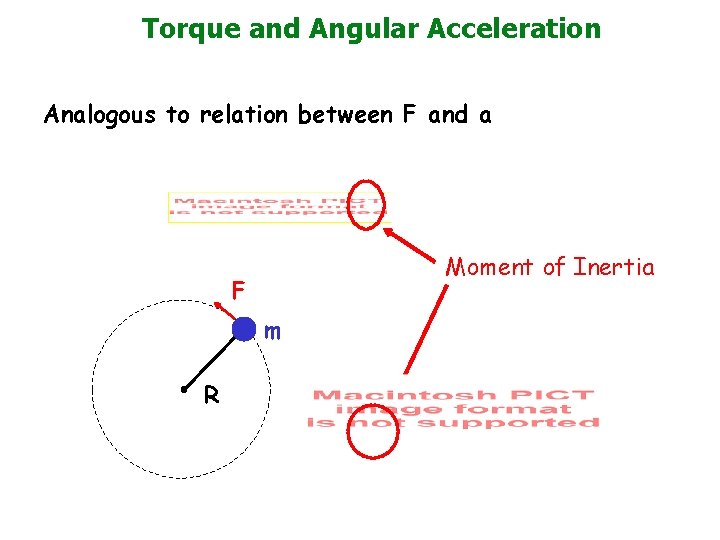
Torque and Angular Acceleration Analogous to relation between F and a Moment of Inertia F m R

Moment of Inertia • Moment of inertia, I: rotational analog to mass • r defined relative to rotation axis • SI units are kg m 2

Baton Demo Moment-of-Inertia Demo

More About Moment of Inertia • Depends on mass and its distribution. • If mass is distributed further from axis of rotation, moment of inertia will be larger.

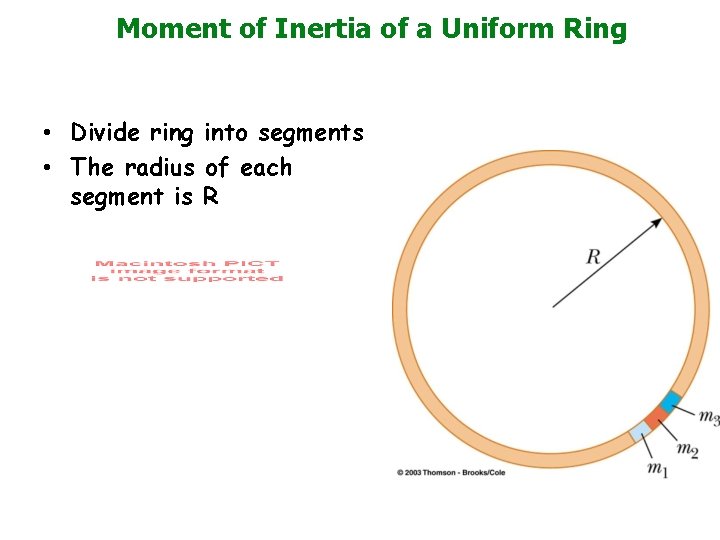
Moment of Inertia of a Uniform Ring • Divide ring into segments • The radius of each segment is R

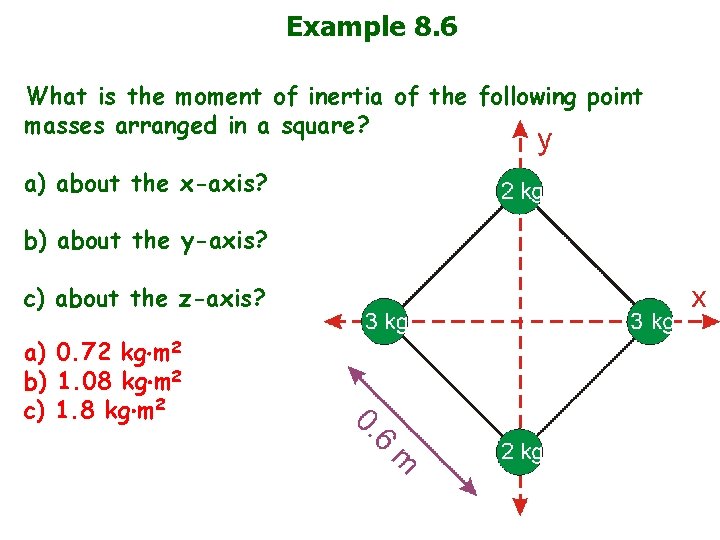
Example 8. 6 What is the moment of inertia of the following point masses arranged in a square? a) about the x-axis? b) about the y-axis? c) about the z-axis? a) 0. 72 kg m 2 b) 1. 08 kg m 2 c) 1. 8 kg m 2

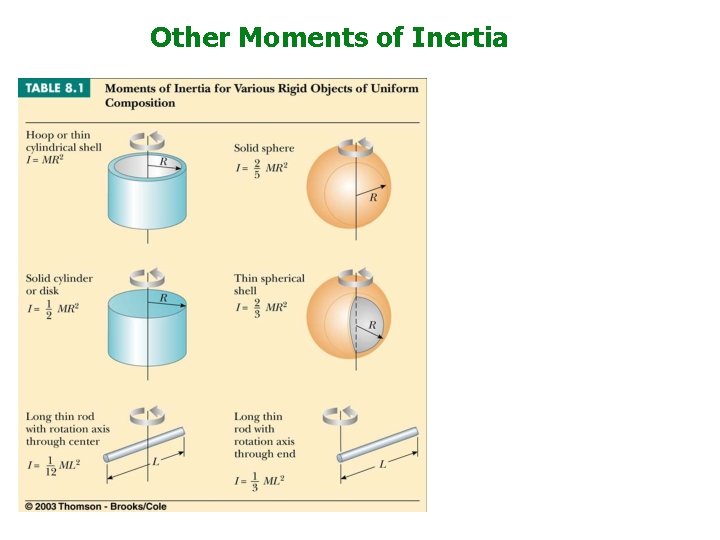
Other Moments of Inertia

Other Moments of Inertia bicycle rim filled can of coke baton baseball bat basketball boulder

Example 8. 7 Treat the spindle as a solid cylinder. a) What is the moment of Inertia of the spindle? (M=5. 0 kg, R=0. 6 m) b) If the tension in the rope is 10 N, what is the angular acceleration of the wheel? c) What is the acceleration of the bucket? M d) What is the mass of the bucket? a) 0. 9 kg m 2 b) 6. 67 rad/s 2 c) 4 m/s 2 d) 1. 72 kg

Example 8. 9 A 600 -kg solid cylinder of radius 0. 6 m which can rotate freely about its axis is accelerated by hanging a 240 kg mass from the end by a string which is wrapped about the cylinder. a) Find the linear acceleration of the mass. 4. 36 m/s 2 b) What is the speed of the mass after it has dropped 2. 5 m? 4. 67 m/s