PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 1 PHYSICS

PHYSICS 231 INTRODUCTORY PHYSICS I Lecture 1

PHYSICS 231 INTRODUCTORY PHYSICS I • Lecturer: Carl Schmidt (Sec. 001) • schmidt@pa. msu. edu • (517) 355 -9200, ext. 2128 • Office Hours: Friday 1 -2: 30 pm in 1248 BPS or by appointment

Course Information http: //www. pa. msu. edu/courses/phy 231

Succeeding in Physics 231 1) Do your homework (yourself) ! 2) Use the help room (1248 BPS) ! 3) Make sure you understand both “why” and “why not” 4) Interrupt the lecturer!

General Physics • First Semester (Phy 231) • Mechanics • Thermodynamics • Simple harmonic motion • Waves Second Semester (Phy 232) • Electromagnetism • Relativity • Modern Physics • (Quantum Mechanics, …, etc. )

Mechanics • Used by all of physics and other sciences • Foundations laid by Galileo and Newton • Newton’s Principia - 1687 Chapter 1: the Basics • SI Units • Unit conversions • Dimensional Analysis • Significant Figures

UNITS (Systéme Internationale) Dimension SI (mks) Unit Definition Length meters (m) Distance traveled by light in 1/(299, 792, 458) s Mass Time kilogram (kg) Mass of a specific platinum- iridium allow cylinder kept by Intl. Bureau of Weights and Measures at Sèvres, France seconds (s) 9, 192, 631, 700 oscillations of cesium atom

Standard Kilogram at Sèvres

Unit conversion Example 1. 1 • A car goes 50 miles/hour. What is that in m/s? 22 m/s

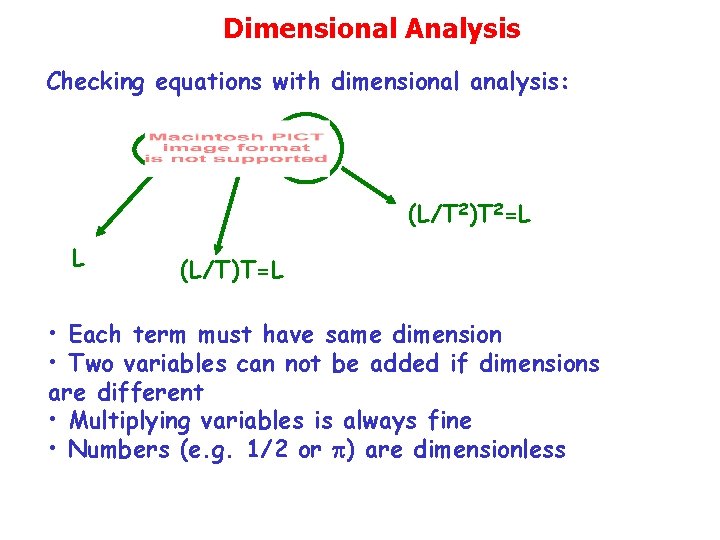
Dimensional Analysis Dimensions (like units) can be treated algebraically. Variable from Eq. x m t v=(xfxi)/t a=(vf-vi)/t Dimension L M T L/T 2

Dimensional Analysis Checking equations with dimensional analysis: (L/T 2)T 2=L L (L/T)T=L • Each term must have same dimension • Two variables can not be added if dimensions are different • Multiplying variables is always fine • Numbers (e. g. 1/2 or p) are dimensionless

Example 1. 2 Could the following equations be correct? No ! Yes, It “could” be.

Units vs. Dimensions: L, T, M, L/T … Units: m, mm, cm, kg, g, mg, s, hr, years … When equation is all algebra: check dimensions When numbers are inserted: check units Units and dimensions obey same rules: Never add terms with different units • Angles are dimensionless but have units (degrees or radians) • In physics sin(Y) or cos(Y) never occur unless Y is dimensionless • • •

Scientific Notation • Useful for very large… Distance to sun = 1500000 m = 1. 5 x 1011 m or small numbers: radius of iron nucleus = 0. 000000044 m = 4. 4 x 10 -15 m

Prefixes In addition to mks units, standard prefixes can be used, e. g. , km, cm, mm

Significant Figures • I measure the table length with my ruler. Which statement is more correct? A. The length is 56. 0 in. (or 5. 60 x 101 in) B. The length is 56. 00 in. (or 5. 600 x 101 in) Statement A. • General Rule: • Number of digits used in decimal or scientific notation (including trailing zeros, but not leading zeros) specifies significant figures (i. e, precision) of measurement.

Significant Figures • Other rules: • When multiplying or dividing, keep the minimum significant figures of any factors: (5. 585)(7. 4) = 41. 329 • When adding or subtracting, keep the least accurate decimal place of any of the numbers: 113. 2 + 2. 54 = 115. 7

Chapter 2: One-Dimensional Motion • Motion at fixed velocity • Definition of average velocity • Motion with fixed acceleration • Graphical representations

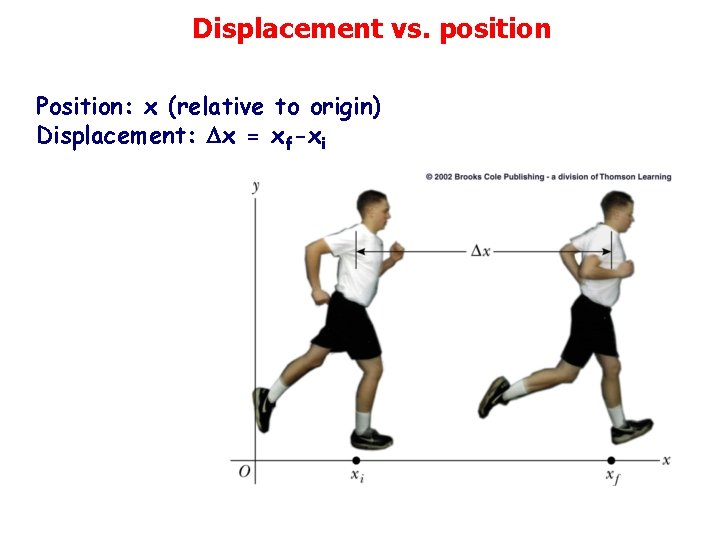
Displacement vs. position Position: x (relative to origin) Displacement: x = xf-xi

Example: Distance vs. Displacement • Distance between Des Moines, Iowa, and Iowa City, is listed as 113. 5 miles or 182. 6 km • Straight line, to very good approximation § Question: • If we take a round trip Des Moines – Iowa City – Des Moines, what is the total distance and displacement for this trip? Distance=365. 2 km Displacement=0

Average velocity • Can be positive or negative • Depends only on initial/final positions • e. g. , if you return to original position, average velocity is zero

Example 2. 1 Carol starts at a position x(t=0) = 1. 5 m. At t=2. 0 s, Carol’s position is x(t=2 s)=4. 5 m At t=4. 0 s, Carol’s position is x(t=4 s)=-2. 5 m a) What is Carol’s average velocity between t=0 and t=2 s? b) What is Carol’s average velocity between t=2 and t=4 s? c) What is Carol’s average velocity between t=0 and t=4 s? a) 1. 5 m/s b) -3. 5 m/s c) -1. 0 m/s

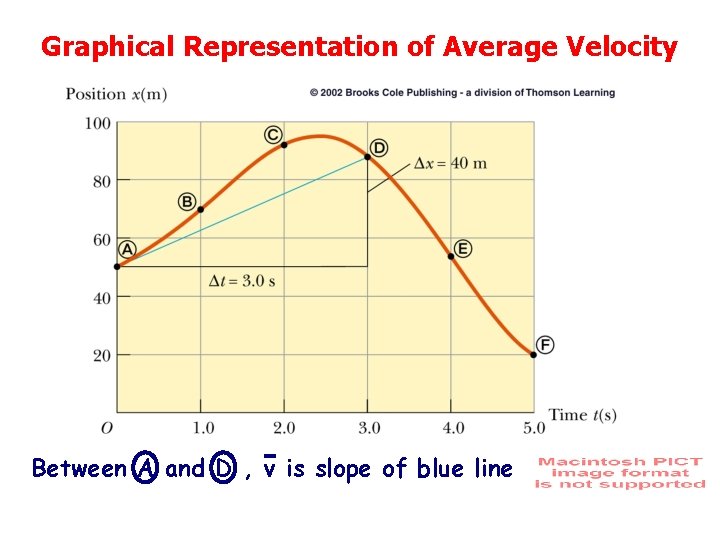
Graphical Representation of Average Velocity Between A and D , v is slope of blue line

Instantaneous velocity Let time interval approach zero • Defined for every instance in time • Equals average velocity if v = constant • SPEED is absolute value of velocity

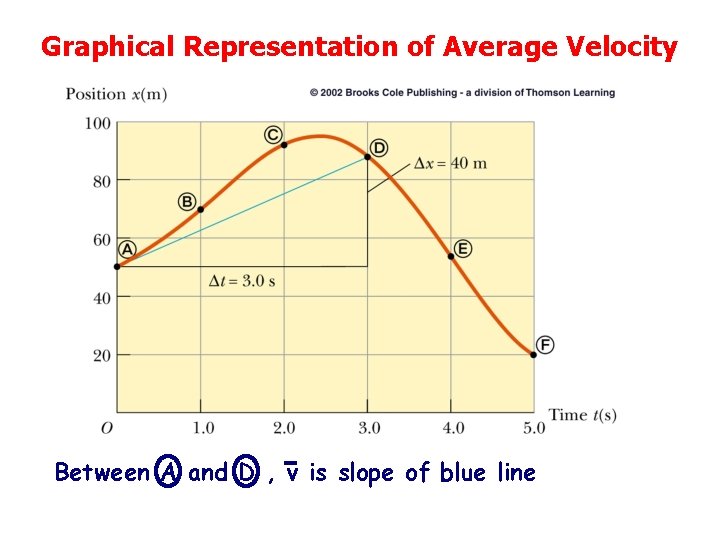
Graphical Representation of Average Velocity Between A and D , v is slope of blue line

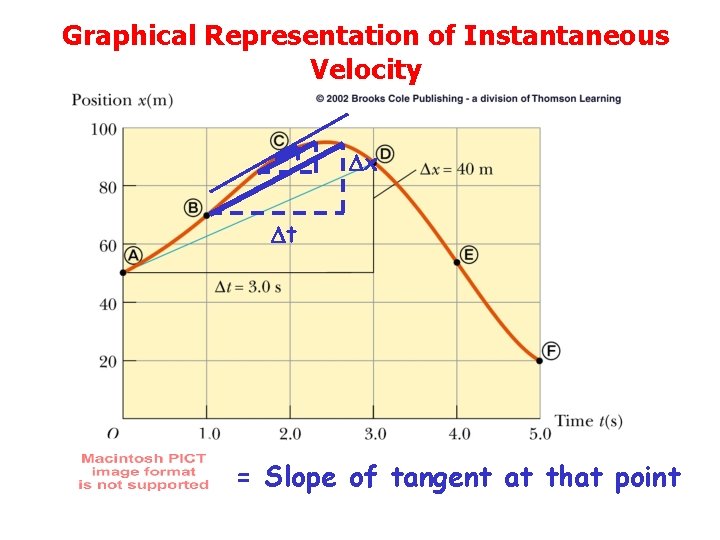
Graphical Representation of Instantaneous Velocity x t = Slope of tangent at that point

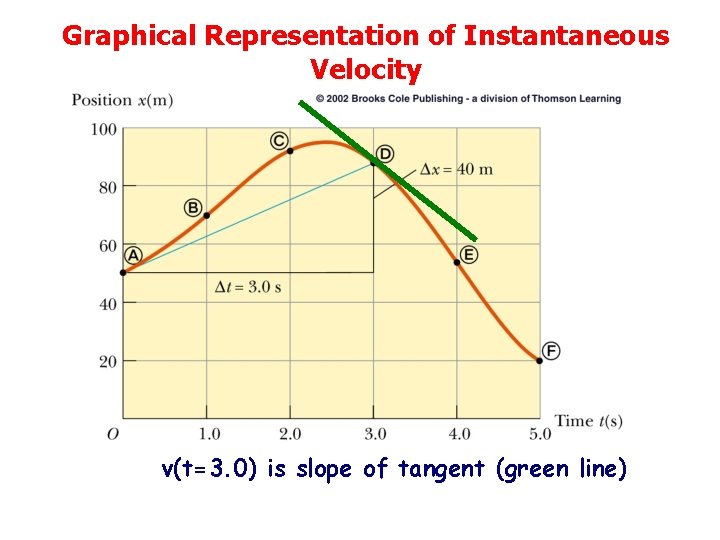
Graphical Representation of Instantaneous Velocity v(t=3. 0) is slope of tangent (green line)

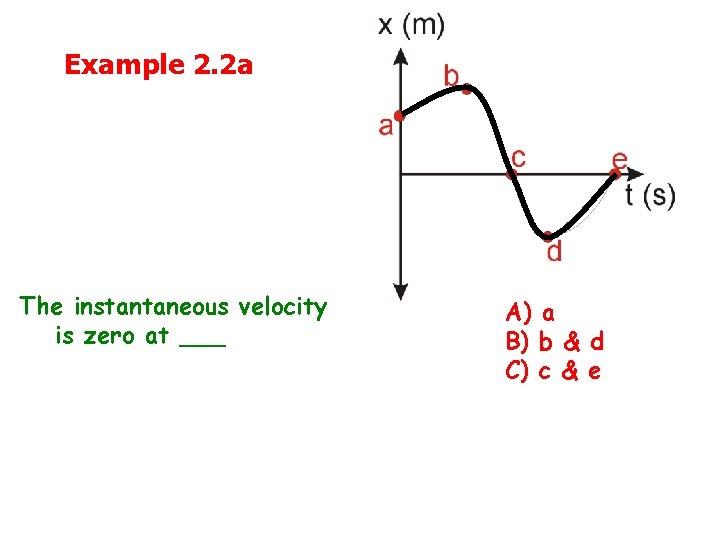
Example 2. 2 a The instantaneous velocity is zero at ___ A) a B) b & d C) c & e

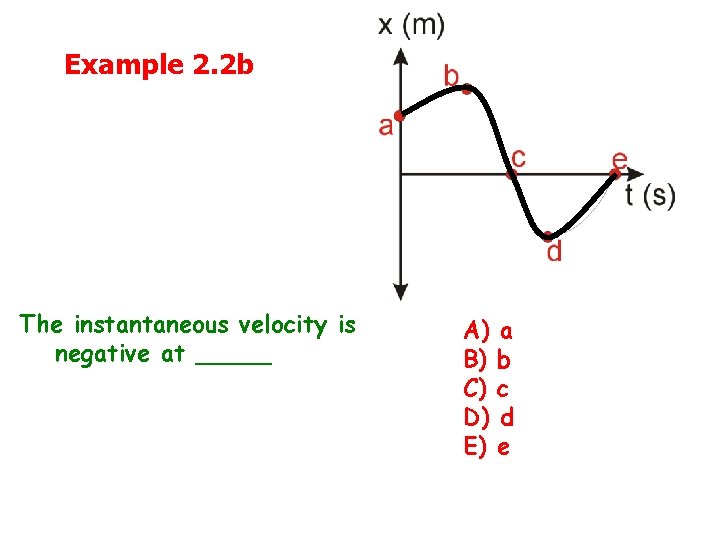
Example 2. 2 b The instantaneous velocity is negative at _____ A) B) C) D) E) a b c d e

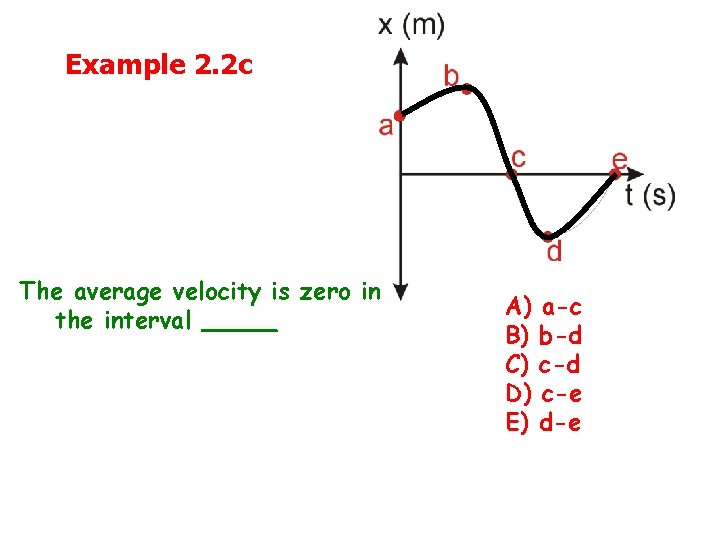
Example 2. 2 c The average velocity is zero in the interval _____ A) B) C) D) E) a-c b-d c-e d-e

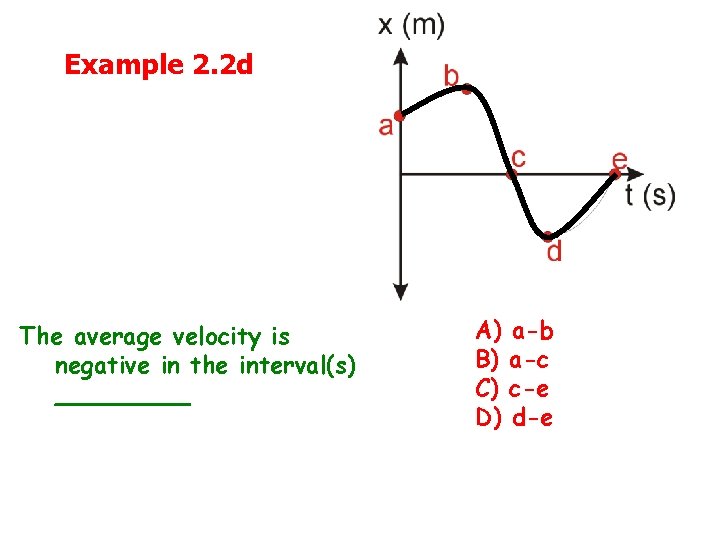
Example 2. 2 d The average velocity is negative in the interval(s) _____ A) B) C) D) a-b a-c c-e d-e

SPEED • Speed is |v| and is always positive • Average speed is sum over | x| elements divided by elapsed time

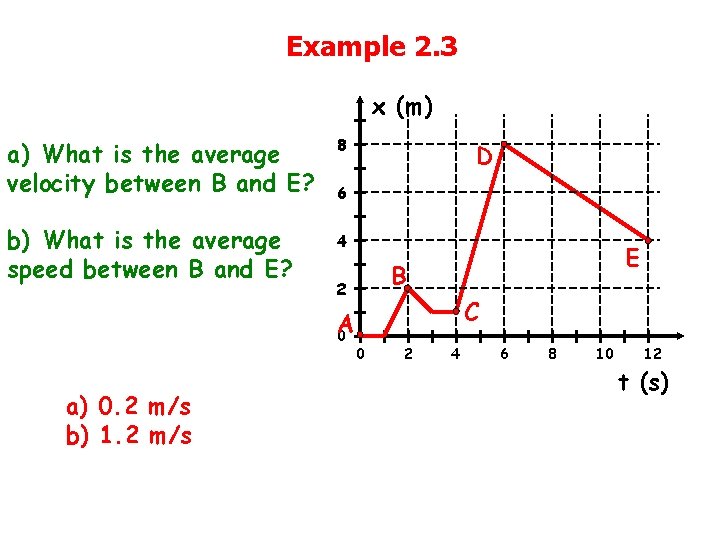
Example 2. 3 x (m) a) What is the average velocity between B and E? 8 b) What is the average speed between B and E? 4 6 E B 2 A 0 a) 0. 2 m/s b) 1. 2 m/s D C 0 2 4 6 8 10 12 t (s)