Physics 212 Lecture 4 Todays Concepts Conductors Using

Physics 212 Lecture 4 Today's Concepts: Conductors + Using Gauss’ Law Applied to Determine E field in cases of high symmetry Physics 212 Lecture 4, Slide 1

Main Point 1 First, Gauss’ law can be used to actually calculate the spatial dependence of the electric field produced by sufficiently symmetric charge distributions. In particular, since we live in a three spatially dimensioned world, there are three kinds of symmetric charge distributions (spherical, cylindrical, and planar) that produced fields that can be calculated directly from Gauss’ law. Physics 212 Lecture 4, Slide 2

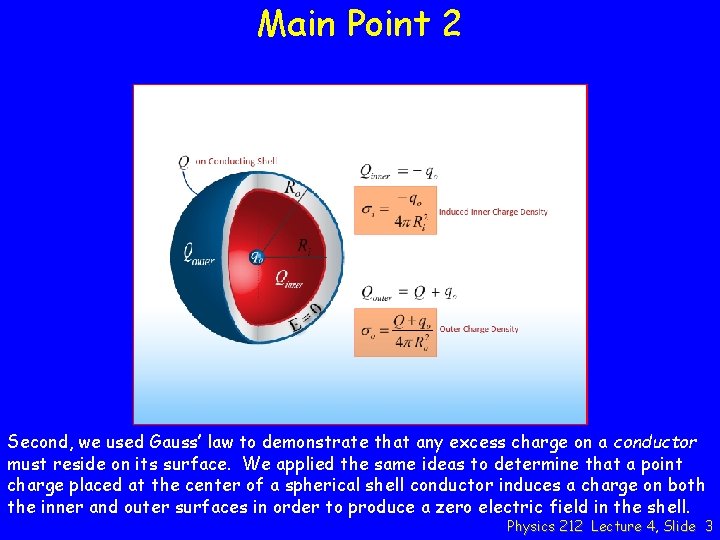
Main Point 2 Second, we used Gauss’ law to demonstrate that any excess charge on a conductor must reside on its surface. We applied the same ideas to determine that a point charge placed at the center of a spherical shell conductor induces a charge on both the inner and outer surfaces in order to produce a zero electric field in the shell. Physics 212 Lecture 4, Slide 3

Main Point 3 We start with the observation that the field lines produced by spherically symmetric charge distributions expand fully into three dimensions; their density decreases as 1/surface area of a sphere or 1/r 2. If we squeeze the spherically symmetric charge distribution into a cylindrically symmetric distribution, the field lines become perpendicular to the axis and can expand only into two dimensions; their density decreases as 1/surface area of a cylinder or 1/r. If we further squeeze the cylindrically symmetric charge distribution into a plane, the field lines become perpendicular to the plane but have no space to expand into. Consequently, their density remains constant leading to a field that is constant over all space. Physics 212 Lecture 4, Slide 4

Conductors = charges free to move Claim: E = 0 inside any conductor at equilibrium Why? Claim: Excess charge on conductor only on surface at equilibrium Why? E = 0 07 Physics 212 Lecture 4, Slide 5

Gauss’ Law ALWAYS TRUE! If choose a Gaussian surface that is entirely in metal, then E=0 so Qenclosed must also be zero! 9 Physics 212 Lecture 4, Slide 6

Physics 212 Lecture 4, Slide 7

Charge in Cavity of Conductor A particle with charge +Q is placed in the center of an uncharged conducting hollow sphere. How much charge will be induced on the inner and outer surfaces of the sphere? A) inner = –Q, outer = +Q B) inner = –Q/2 , outer = +Q/2 C) inner = 0, Qouter Qinner outer = 0 D) inner = +Q/2, outer = -Q/2 Q E) inner = +Q, outer = -Q 11 Physics 212 Lecture 4, Slide 8

Infinite Cylinders A long thin wire has a uniform positive charge density of 2. 5 C/m. Concentric with the wire is a long thick conducting cylinder, with inner radius 3 cm, and outer radius 5 cm. The conducting cylinder has a net linear charge density of -4 C/m. What is the linear charge density of the induced charge on the inner surface of the conducting cylinder? A) -6. 5 C/m B) -4 C/m C) -2. 5 C/m D) -1. 5 C/m E) 0 What is the linear charge density of the induced charge on the outer surface of the conducting cylinder? A) -4 C/m B) -2. 5 C/m C) -1. 5 C/m D) 0 C/m E) +2. 5 C/m Physics 212 Lecture 4, Slide 9

Gauss’ Law Symmetries ALWAYS TRUE! In cases with symmetry can pull E outside and get Spherical 22 Cylindrical Planar Physics 212 Lecture 4, Slide 10

Physics 212 Lecture 4, Slide 11

Checkpoint 1 (D) The field cannot be calculated using Gauss’ Law (E) None of the above 23 Physics 212 Lecture 4, Slide 12

Checkpoint 2 33 Physics 212 Lecture 4, Slide 13

Checkpoint 3 30 Physics 212 Lecture 4, Slide 14

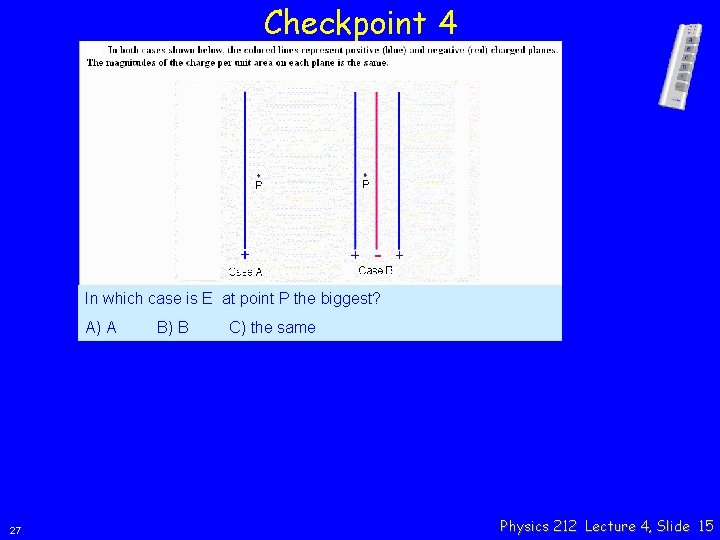
Checkpoint 4 In which case is E at point P the biggest? A) A 27 B) B C) the same Physics 212 Lecture 4, Slide 15

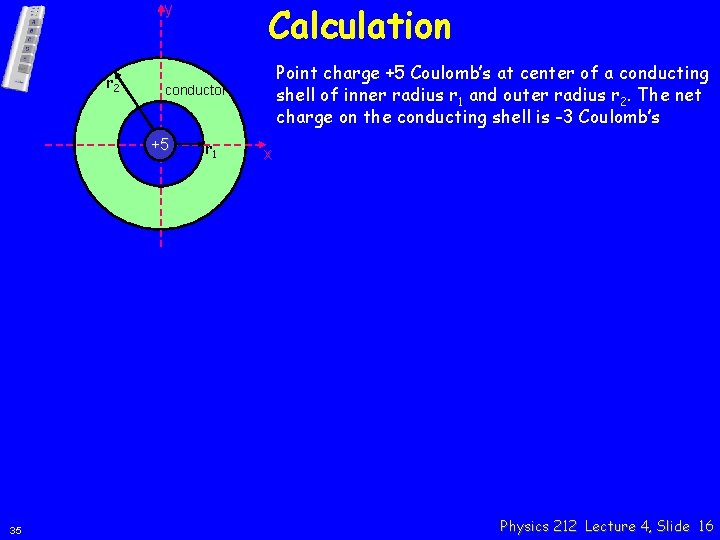
Calculation y r 2 conductor +5 35 Point charge +5 Coulomb’s at center of a conducting shell of inner radius r 1 and outer radius r 2. The net charge on the conducting shell is -3 Coulomb’s r 1 x Physics 212 Lecture 4, Slide 16

Physics 212 Lecture 4, Slide 17

Physics 212 Lecture 4, Slide 18