Physics 212 Lecture 19 LC and RLC Circuits

Physics 212 Lecture 19 LC and RLC Circuits - Oscillation frequency Energy Damping Physics 212 Lecture 19, Slide 1

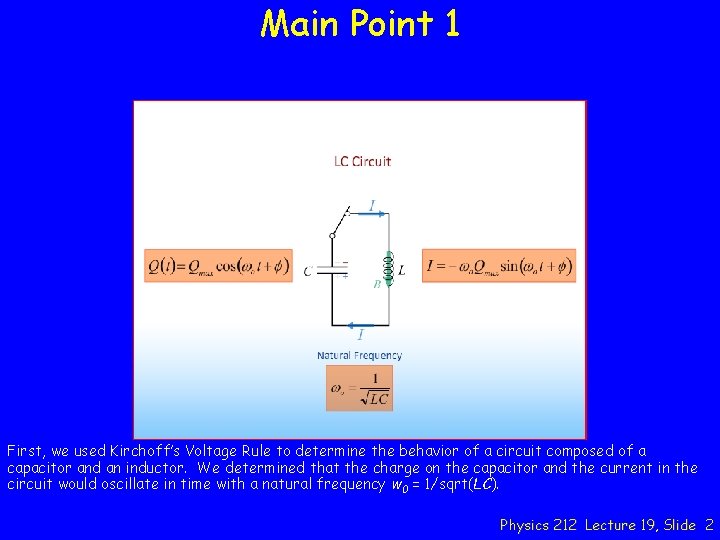
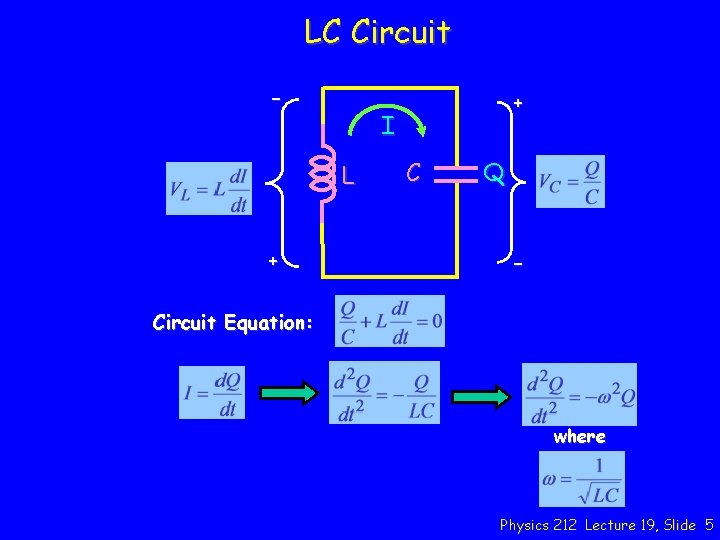
Main Point 1 First, we used Kirchoff’s Voltage Rule to determine the behavior of a circuit composed of a capacitor and an inductor. We determined that the charge on the capacitor and the current in the circuit would oscillate in time with a natural frequency w 0 = 1/sqrt(LC). Physics 212 Lecture 19, Slide 2

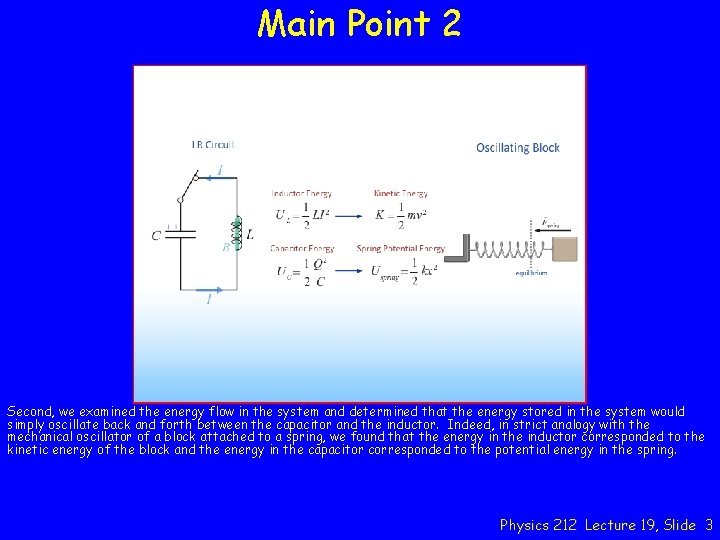
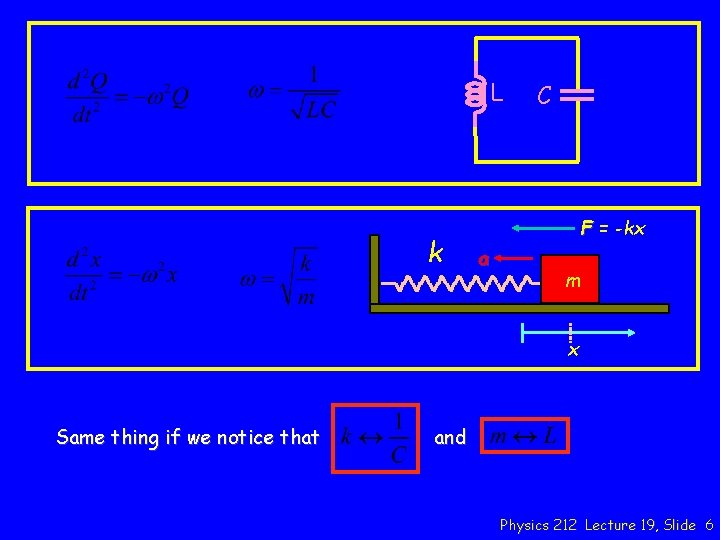
Main Point 2 Second, we examined the energy flow in the system and determined that the energy stored in the system would simply oscillate back and forth between the capacitor and the inductor. Indeed, in strict analogy with the mechanical oscillator of a block attached to a spring, we found that the energy in the inductor corresponded to the kinetic energy of the block and the energy in the capacitor corresponded to the potential energy in the spring. Physics 212 Lecture 19, Slide 3

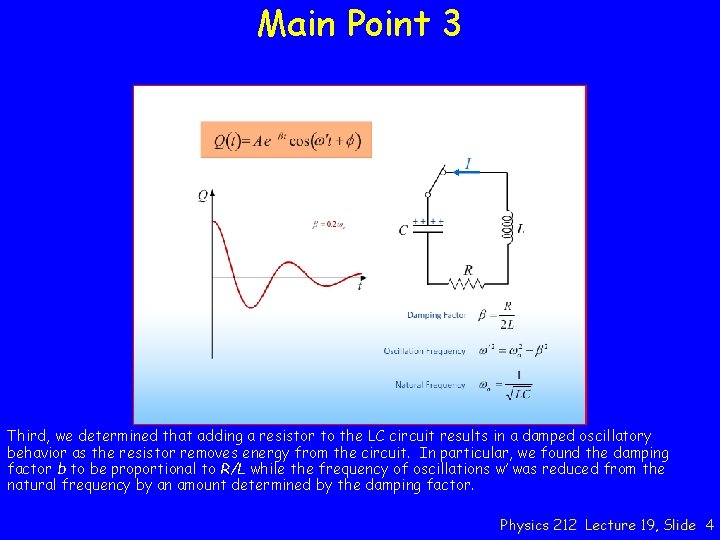
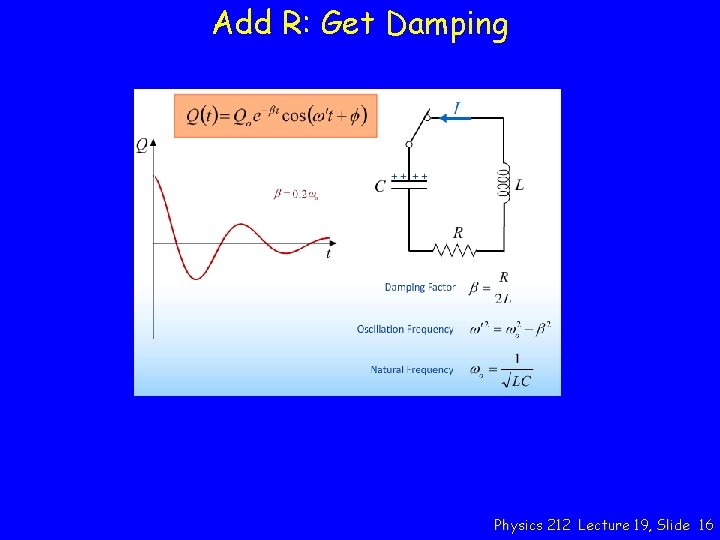
Main Point 3 Third, we determined that adding a resistor to the LC circuit results in a damped oscillatory behavior as the resistor removes energy from the circuit. In particular, we found the damping factor b to be proportional to R/L while the frequency of oscillations w’ was reduced from the natural frequency by an amount determined by the damping factor. Physics 212 Lecture 19, Slide 4

LC Circuit - I L + + C Q - Circuit Equation: where Physics 212 Lecture 19, Slide 5

L k C F = -kx a m x Same thing if we notice that and Physics 212 Lecture 19, Slide 6

Physics 212 Lecture 19, Slide 7

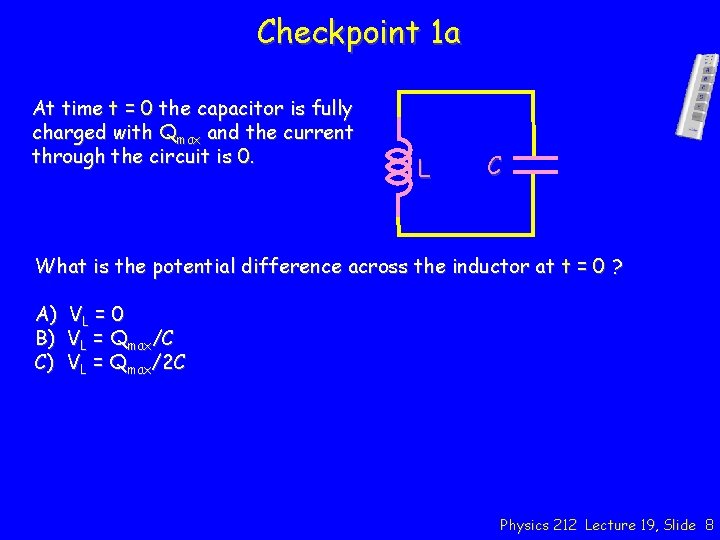
Checkpoint 1 a At time t = 0 the capacitor is fully charged with Qmax and the current through the circuit is 0. L C What is the potential difference across the inductor at t = 0 ? A) VL = 0 B) VL = Qmax/C C) VL = Qmax/2 C Physics 212 Lecture 19, Slide 8

Checkpoint 1 b At time t = 0 the capacitor is fully charged with Qmax and the current through the circuit is 0. L C What is the potential difference across the inductor when the current is maximum ? A) VL = 0 B) VL = Qmax/C C) VL = Qmax/2 C Physics 212 Lecture 19, Slide 9

Checkpoint 1 c At time t = 0 the capacitor is fully charged with Qmax and the current through the circuit is 0. L C How much energy is stored in the capacitor when the current is a maximum ? A) U = Qmax 2/(2 C) B) U = Qmax 2/(4 C) C) U = 0 Physics 212 Lecture 19, Slide 10

Physics 212 Lecture 19, Slide 11

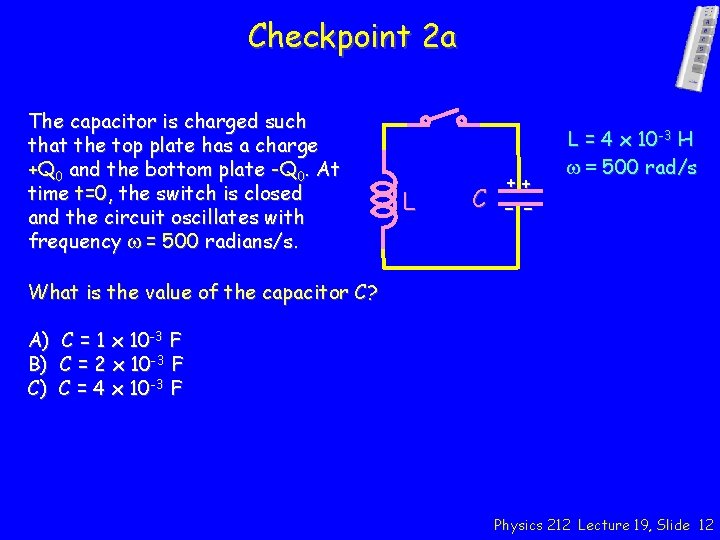
Checkpoint 2 a The capacitor is charged such that the top plate has a charge +Q 0 and the bottom plate -Q 0. At time t=0, the switch is closed and the circuit oscillates with frequency w = 500 radians/s. L C ++ -- L = 4 x 10 -3 H w = 500 rad/s What is the value of the capacitor C? A) C = 1 x 10 -3 F B) C = 2 x 10 -3 F C) C = 4 x 10 -3 F Physics 212 Lecture 19, Slide 12

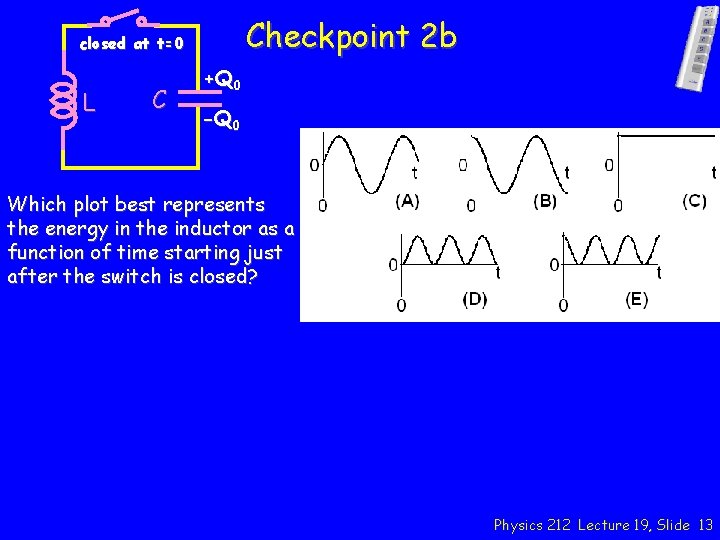
Checkpoint 2 b closed at t=0 L C +Q 0 -Q 0 Which plot best represents the energy in the inductor as a function of time starting just after the switch is closed? Physics 212 Lecture 19, Slide 13

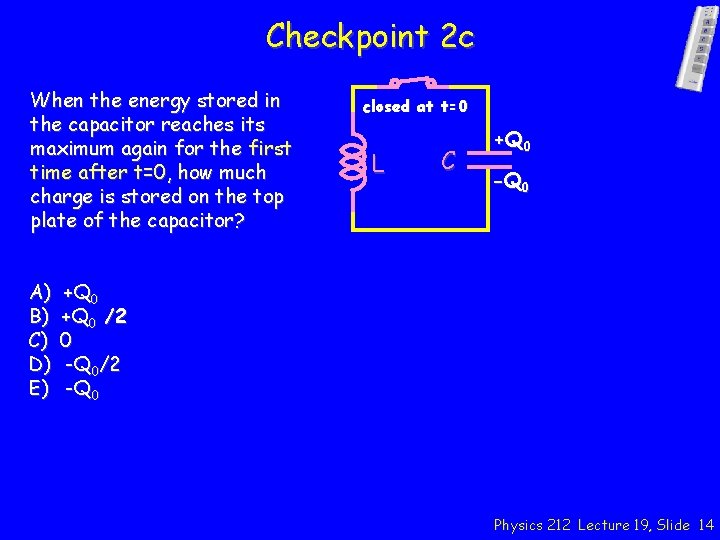
Checkpoint 2 c When the energy stored in the capacitor reaches its maximum again for the first time after t=0, how much charge is stored on the top plate of the capacitor? closed at t=0 L C +Q 0 -Q 0 A) +Q 0 B) +Q 0 /2 C) 0 D) -Q 0/2 E) -Q 0 Physics 212 Lecture 19, Slide 14

Physics 212 Lecture 19, Slide 15

Add R: Get Damping Physics 212 Lecture 19, Slide 16

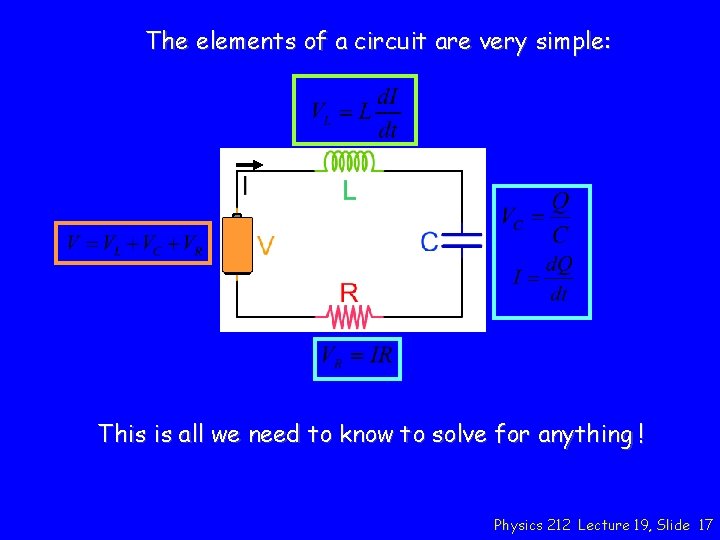
The elements of a circuit are very simple: This is all we need to know to solve for anything ! Physics 212 Lecture 19, Slide 17

Physics 212 Lecture 19, Slide 18

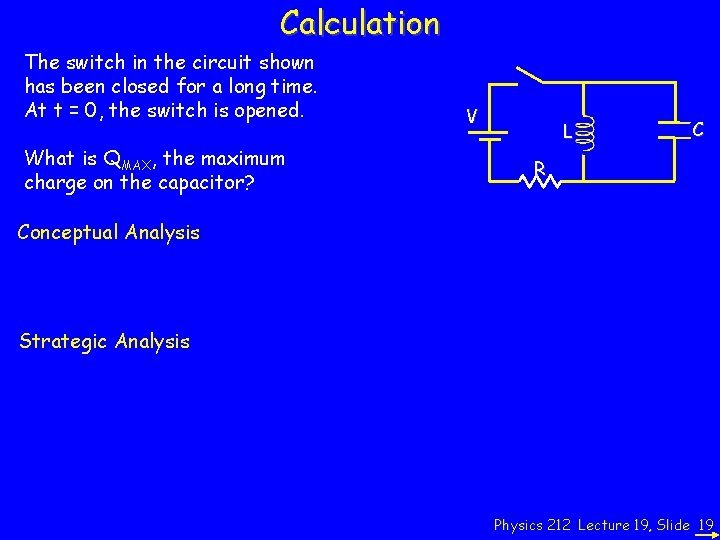
Calculation The switch in the circuit shown has been closed for a long time. At t = 0, the switch is opened. What is QMAX, the maximum charge on the capacitor? V L C R Conceptual Analysis Strategic Analysis Physics 212 Lecture 19, Slide 19

Physics 212 Lecture 19, Slide 20

Physics 212 Lecture 19, Slide 21

Physics 212 Lecture 19, Slide 22