Physics 2102 Jonathan Dowling Physics 2102 Exam 2











![Problem: 27. P. 018. [406649] Figure 27 -33 shows five 5. 00 resistors. (Hint: Problem: 27. P. 018. [406649] Figure 27 -33 shows five 5. 00 resistors. (Hint:](https://slidetodoc.com/presentation_image_h/19560dfaae10950877a9c8e2f7b74197/image-20.jpg)
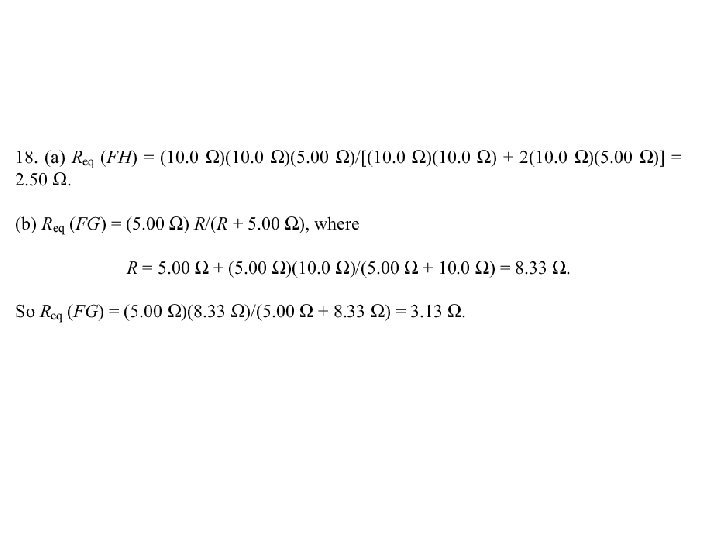
![Problem: 27. P. 046. [406629] In an RC series circuit, E = 17. 0 Problem: 27. P. 046. [406629] In an RC series circuit, E = 17. 0](https://slidetodoc.com/presentation_image_h/19560dfaae10950877a9c8e2f7b74197/image-22.jpg)



![Problem: 28. P. 024. [566302] In the figure below, a charged particle moves into Problem: 28. P. 024. [566302] In the figure below, a charged particle moves into](https://slidetodoc.com/presentation_image_h/19560dfaae10950877a9c8e2f7b74197/image-30.jpg)



- Slides: 33

Physics 2102 Jonathan Dowling Physics 2102 Exam 2: Review Session Chapters 24. 9 -28. 8 / HW 04 -06 Some links on exam stress: http: //appl 003. lsu. edu/slas/cas. nsf/$Content/Stress+Management+Tip+1 http: //wso. williams. edu/orgs/peerh/stress/exams. html http: //www. thecalmzone. net/Home/Exam. Stress. php http: //www. staithes. demon. co. uk/exams. html

Exam 2 • (Ch 24) Sec. 11 (Electric Potential Energy of a System of Point Charges); Sec. 12 (Potential of Charged Isolated Conductor) • (Ch 25) Capacitors: capacitance and capacitors; caps in parallel and in series, dielectrics; energy, field and potential in capacitors. • (Ch 26) Current and Resistance: Resistance current, current density and drift velocity; resistance and resistivity; Ohm’s law. • (Ch 27) Circuits: emf devices, loop and junction rules; resistances in series and parallel; DC single and multiloop circuits, power; RC circuits. • (Ch 28) Magnetic Fields: F=vx. B, Right Hand Rule, Circular Motion, Force on Wire, Magnetic Dipole.

Potential V of Continuous Charge Distributions Straight Line Charge: dq= dx =Q/L Curved Line Charge: dq= ds =Q/2 R Surface Charge: dq= d. A =Q/ R 2 d. A=2 R’d. R’

Potential V of Continuous Charge Distributions Curved Line Charge: dq= ds =Q/2 R Straight Line Charge: dq= dx =Q/L

Potential V of Continuous Charge Distributions Surface Charge: dq= d. A =Q/ R 2 d. A=R’d. R’d Straight Line Charge: dq= dx =bx is given to you.

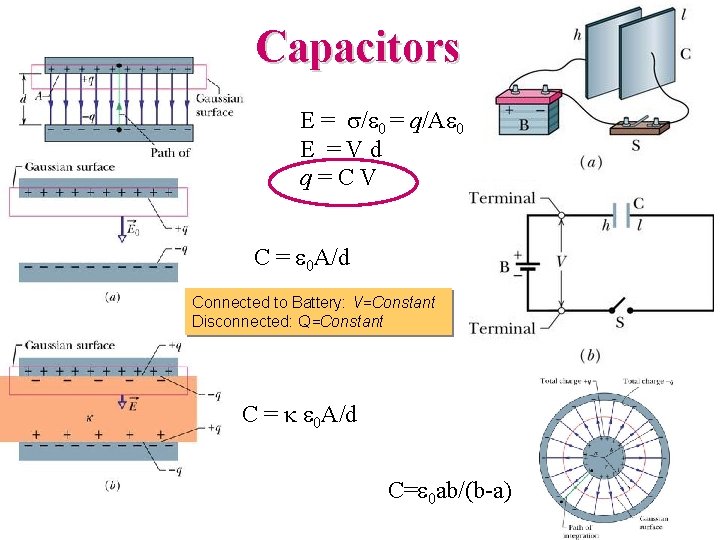
Capacitors E = s/e 0 = q/Ae 0 E =Vd q=CV C = e 0 A/d Connected to Battery: V=Constant Disconnected: Q=Constant C = k e 0 A/d C=e 0 ab/(b-a)

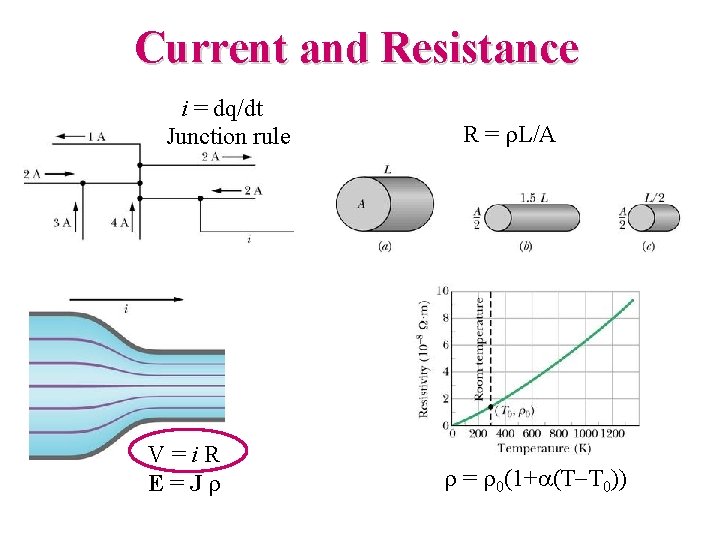
Current and Resistance i = dq/dt Junction rule V=i. R E=Jr R = r. L/A r = r 0(1+a(T-T 0))

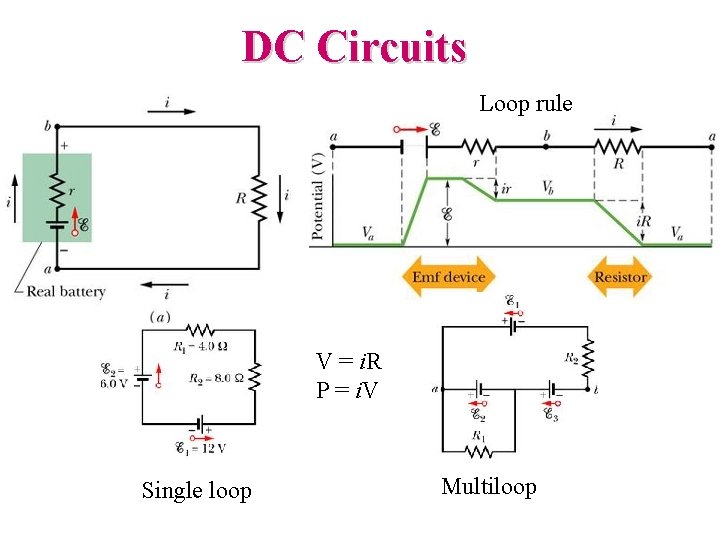
DC Circuits Loop rule V = i. R P = i. V Single loop Multiloop

Resistors and Capacitors Resistors Key formula: V=i. R In series: same current Req=∑Rj In parallel: same voltage 1/Req= ∑ 1/Rj Capacitors Q=CV same charge 1/Ceq= ∑ 1/Cj same voltage Ceq=∑Cj

Capacitors and Resistors in Series and in Parallel • What’s the equivalent resistance (capacitance)? • What’s the current (charge) in each resistor (capacitor)? • What’s the potential across each resistor (capacitor)? • What’s the current (charge) delivered by the battery?

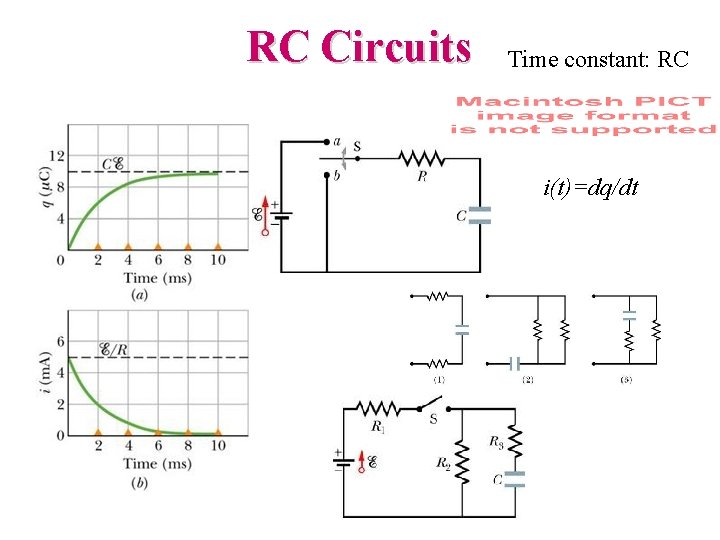
RC Circuits Time constant: RC i(t)=dq/dt

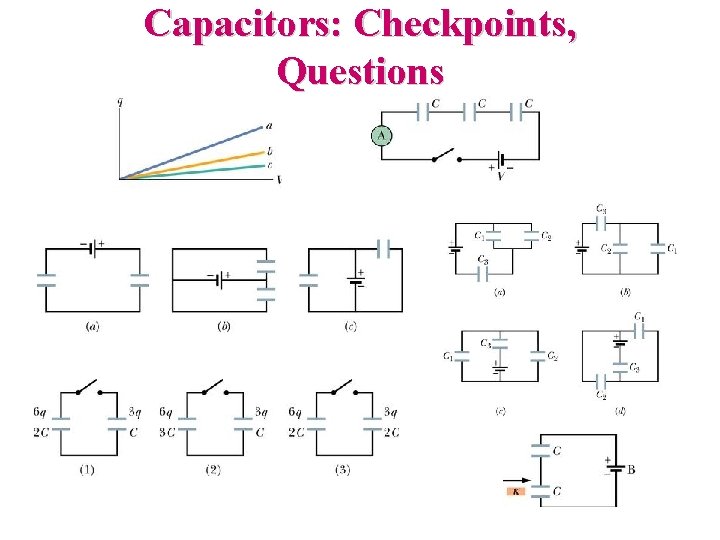
Capacitors: Checkpoints, Questions

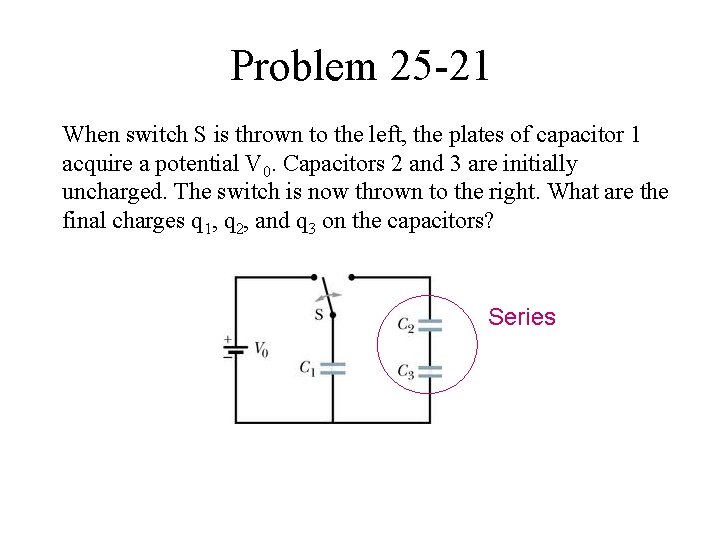
Problem 25 -21 When switch S is thrown to the left, the plates of capacitor 1 acquire a potential V 0. Capacitors 2 and 3 are initially uncharged. The switch is now thrown to the right. What are the final charges q 1, q 2, and q 3 on the capacitors? Series

Series Seri-Q


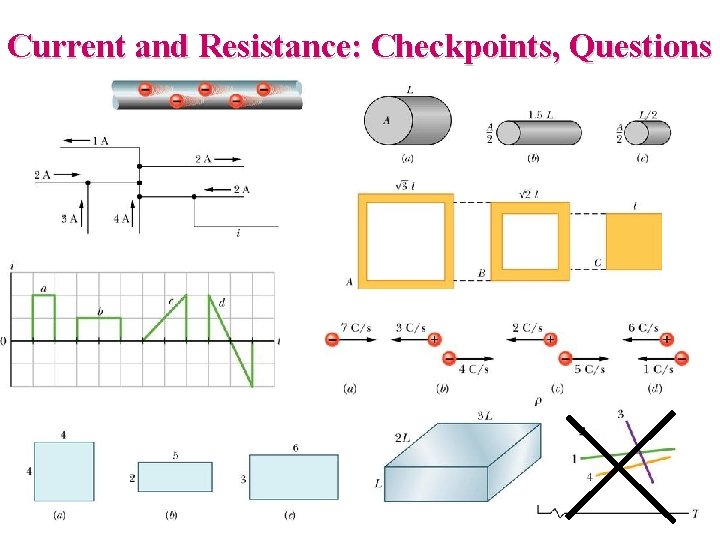
Current and Resistance: Checkpoints, Questions

Problem 26 -56 A cylindrical resistor of radius 5. 0 mm and length 2. 0 cm is made of a material that has a resistivity of 3. 5 x 10 -5 m. What are the (a) current density and (b) the potential difference when the energy dissipation rate in the resistor is 1. 0 W?


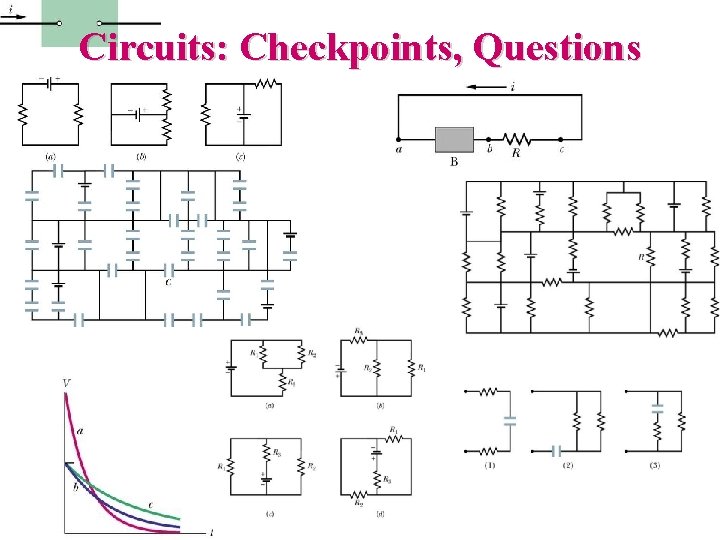
Circuits: Checkpoints, Questions
![Problem 27 P 018 406649 Figure 27 33 shows five 5 00 resistors Hint Problem: 27. P. 018. [406649] Figure 27 -33 shows five 5. 00 resistors. (Hint:](https://slidetodoc.com/presentation_image_h/19560dfaae10950877a9c8e2f7b74197/image-20.jpg)
Problem: 27. P. 018. [406649] Figure 27 -33 shows five 5. 00 resistors. (Hint: For each pair of points, imagine that a battery is connected across the pair. ) Fig. 27 -33 (a) Find the equivalent resistance between points F and H. (b) Find the equivalent resistance between points F and G.
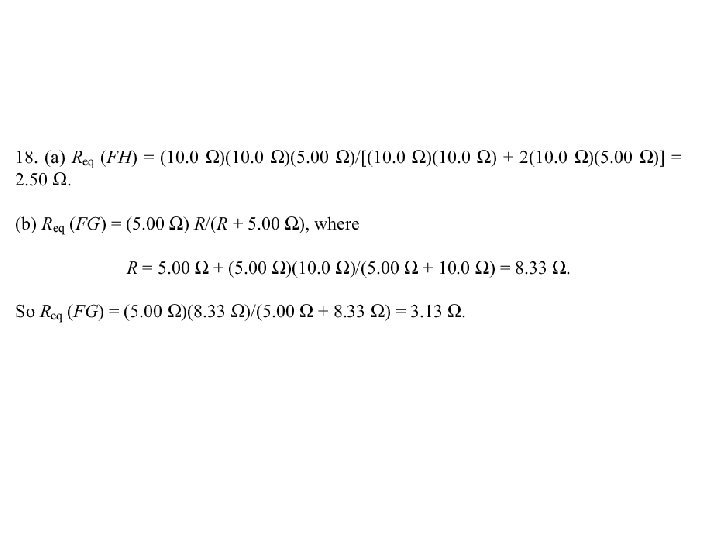
![Problem 27 P 046 406629 In an RC series circuit E 17 0 Problem: 27. P. 046. [406629] In an RC series circuit, E = 17. 0](https://slidetodoc.com/presentation_image_h/19560dfaae10950877a9c8e2f7b74197/image-22.jpg)
Problem: 27. P. 046. [406629] In an RC series circuit, E = 17. 0 V, R = 1. 50 M , and C = 1. 80 µF. (a) Calculate the time constant. (b) Find the maximum charge that will appear on the capacitor during charging. (c) How long does it take for the charge to build up to 10. 0 µC?


Magnetic Forces and Torques v F L

Side view Top view C C (28 -13)

(28 -14)

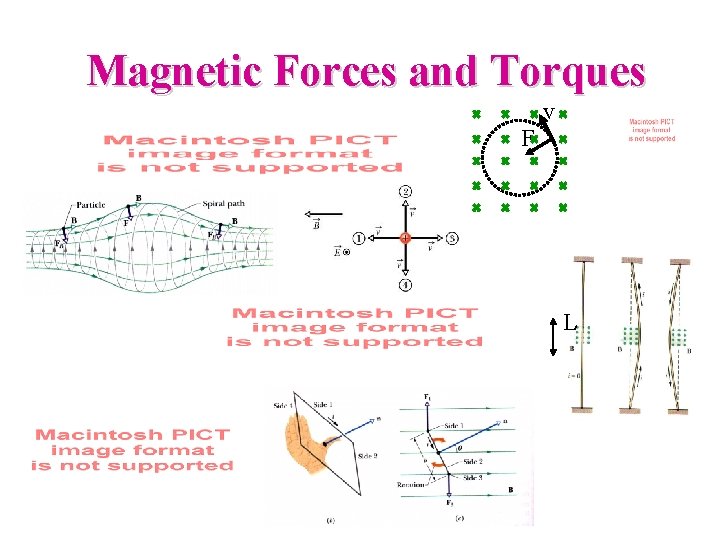
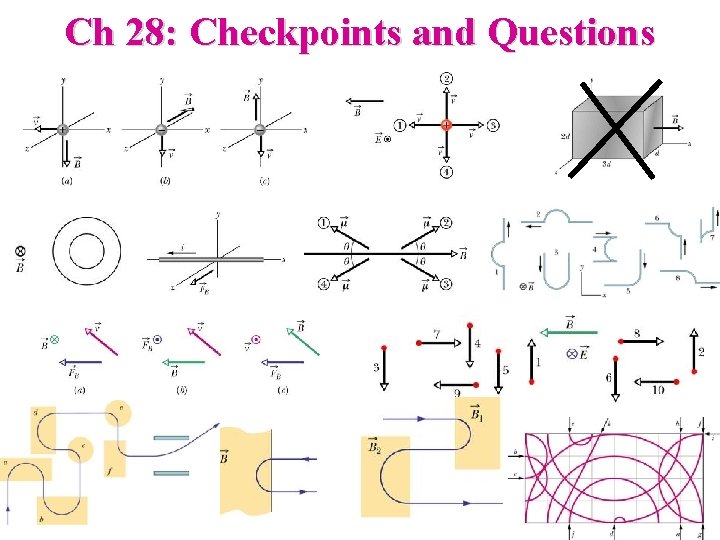
Ch 28: Checkpoints and Questions

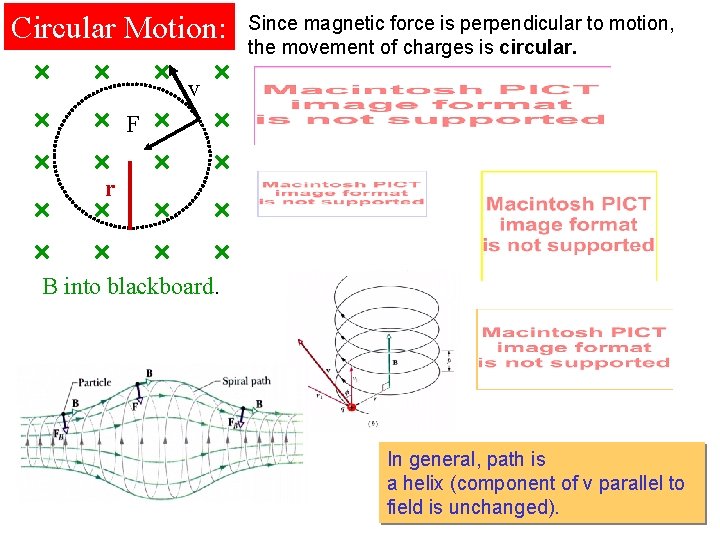
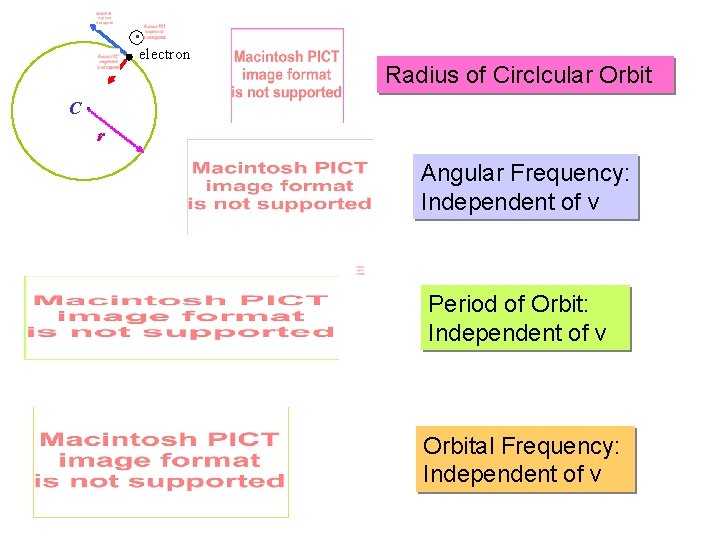
Circular Motion: Since magnetic force is perpendicular to motion, the movement of charges is circular. v F r B into blackboard. In general, path is a helix (component of v parallel to field is unchanged).

. electron C . Radius of Circlcular Orbit r Angular Frequency: Independent of v Period of Orbit: Independent of v Orbital Frequency: Independent of v
![Problem 28 P 024 566302 In the figure below a charged particle moves into Problem: 28. P. 024. [566302] In the figure below, a charged particle moves into](https://slidetodoc.com/presentation_image_h/19560dfaae10950877a9c8e2f7b74197/image-30.jpg)
Problem: 28. P. 024. [566302] In the figure below, a charged particle moves into a region of uniform magnetic field , goes through half a circle, and then exits that region. The particle is either a proton or an electron (you must decide which). It spends 160 ns in the region. (a) What is the magnitude of B? (b) If the particle is sent back through the magnetic field (along the same initial path) but with 3. 00 times its previous kinetic energy, how much time does it spend in the field during this trip?


