Physics 201 9 Rotation of Rigid Objects Angular

Physics 201 9: Rotation of Rigid Objects • Angular Velocity and Angular Acceleration • Rotational Kinetics • Relationship between Angular and Linear Quantities • Rotational Kinetic Energy • Calculation of Moments of Inertia • Torque and Angular Acceleration • Work and Energy in Rotational Motion

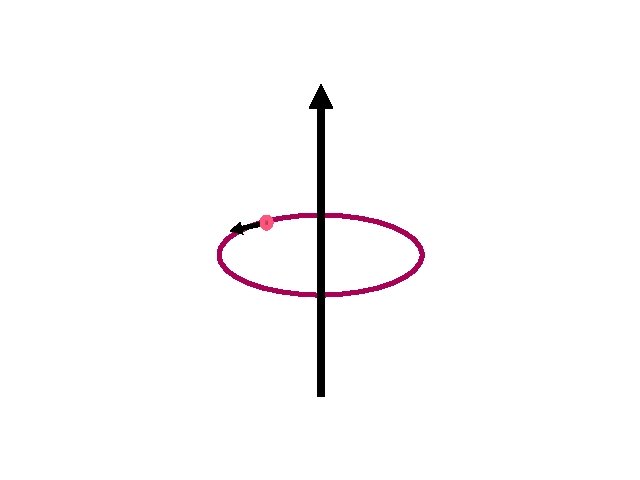
Angular Velocity and Angular Acceleration Recall the following definitions s angular (radian) distance q = r s = length of arc that subtends angle q at center of circle of radius r q increases in the anticlockwise direction around the axis of rotation ˆb q = q bˆ angular displacement angular speed w = angular velocity angular acceleration dq dt dq ˆ b w = dt dw ˆ b a = dt

Rotational Kinetics The angular version of the kinetic equations of motion for rotations with constant angular acceleration 1 2 q(t ) = a t + w(t 0 )t 2 w(t ) = a t+ w(t 0 ) [note that q(t) is angular displacement q(t ) = q(t f ) - q(ti ) ]

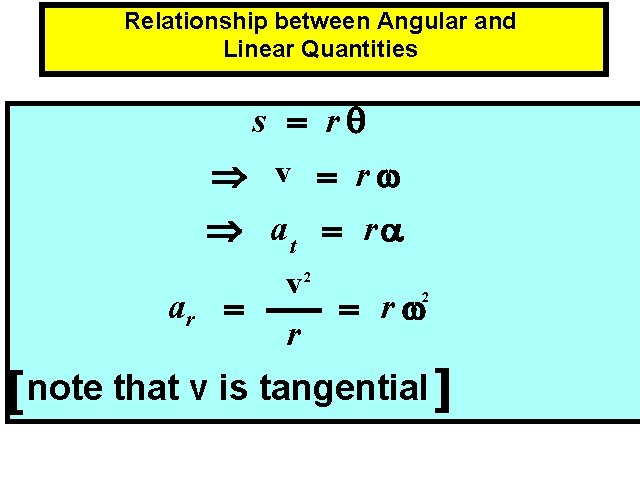
Relationship between Angular and Linear Quantities s = rq Þ v = rw Þ at = r a ar = v 2 r = rw 2 [ note that v is tangential ]

Rotational Kinetic Energy K = 1 1 mv 2 = m r 2 w 2 2 2 Define the Moment of inertia I of the mass m about the rotational axis as I = mr 2 I has SI units kgm 2 Then the kinetic energy of the mass m rotating about a fixed axis at a fixed perpendicular distance r is 1 2 Iw 2 If there are many masses rotating at fixed distances K = about a fixed axis then K tot = I = å i mi ri 2 1 Iw 2 2 = moment of inertia of the system

Calculation of Moments of Inertia For Extended System First one must choose the axis of rotation Then divide system into small masses Dm ( r ) centered at the position r å I = Then 2 Dm ( ri ) r i i for extended objects æ Lim ç I = D m ( ri) ¯ 0 è å D m ( r i) r 2 i i noting that dm I = ò ö ÷ = ø ò r 2 dm object = r ( r ) d. V r 2 r ( r ) d. V object If the object is homogeneous r ( r ) = constant I = r ò object r 2 d. V

To obtain the moment of inertia about some other axis that is a distance D away from the symmetry axis we can apply the PARALLEL AXIS THEOREM The Moment of Inertia about any axis that is parallel to and a distance D away from the axis that passes through the center of mass is given by I = I cm + MD 2

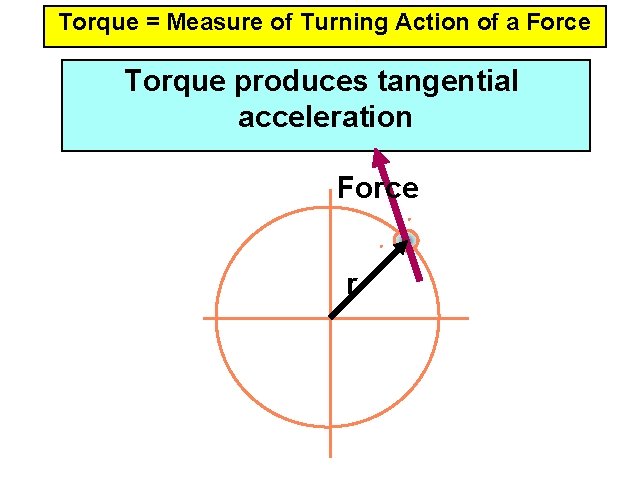
Torque = Measure of Turning Action of a Force Torque produces tangential acceleration Force r

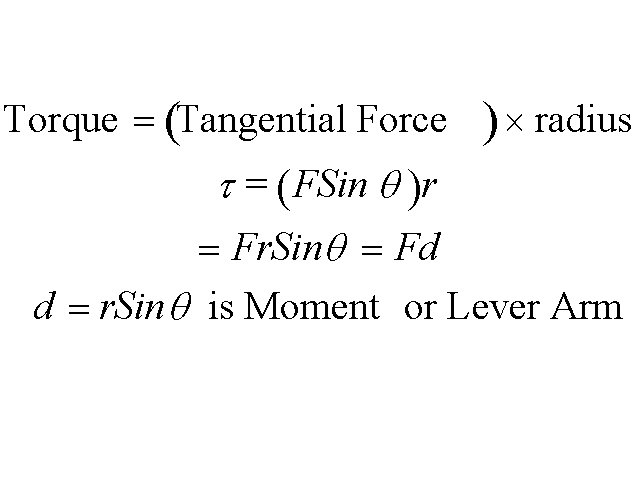
Torque = (Tangential Force ) ´ radius t = ( FSin q )r = Fr. Sinq = Fd d = r. Sin q is Moment or Lever Arm

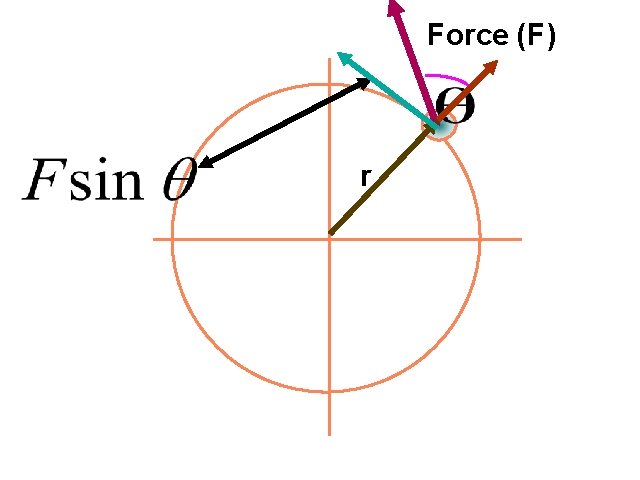
Force (F) r

Vector Product a´b ^ a a´b ^ b a ´ b = a b sin q q is the angle between a and b

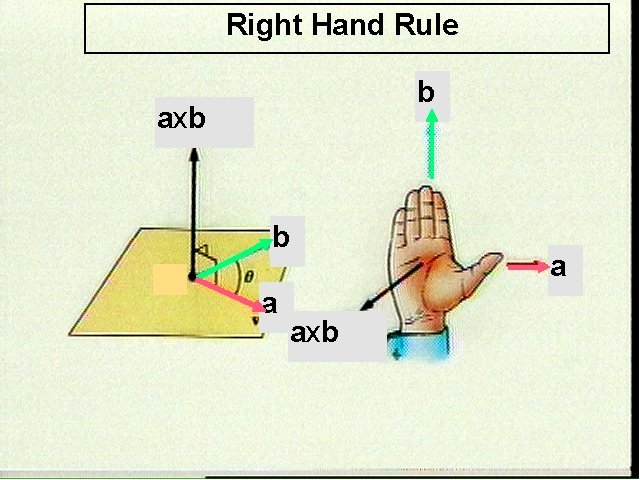
Right Hand Rule b axb b a axb a

Vector Product i a ´ b = a b (a y b z - a zb y j a x b x )i - ( a x b k a y b y - a zb z = -b ´ a = z z x )j + (a i j k i ´ j = 1 0 0 = k 0 1 0 j ´ k = i j k 0 1 0 = i 0 0 1 i j k i ´ k = 1 0 0 = - j 0 0 1 x b y - ayb x )k

k right handed axis system j i

Using the vector product Torque can be written as t =r´F r = ^ displacement vector from the axis to the point of contact of the force F unit vector in direction of rotational axis is ˆ = tˆ ˆr ´ F t t = r Ft = rma t = rmr a= mr 2 a t = Ia Angular version of Newtons Second Law [valid for system of particles and extended system ]

Work and Energy in Rotational Motion ^ d. W = F · d s = F · rdq d s = Ft rd q = t d q W = ò q qf td q i Thus if torque is constant W = t. Dq ^ ^

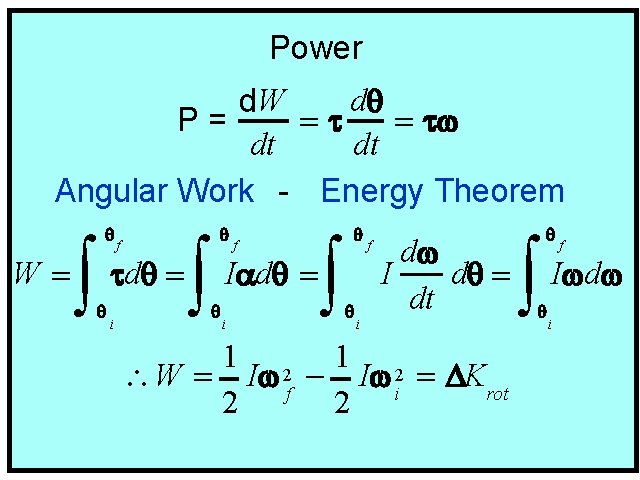
Power dq d. W P= =t = tw dt dt Angular Work - Energy Theorem W= ò qf q tdq = i ò qf Iadq = q i ò qf q dw I dq = dt i 1 2 W = Iw f - Iw i = DKrot 2 2 ò qf q Iwdw i

Torque of a force on an object that is a distance r from an axis of rotation t = Ft r = Fr sin q = Fd Angular form of Newtons Second Law t = Ia Rotational K. E. 1 K rot = Iw 2 2 Angular form of the Work - Energy theorem W = D Krot Angular Work W = ò q f td q q i Angular Power P = tw