Physics 201 13 Oscillatory Motion Simple Harmonic Motion

Physics 201 13: Oscillatory Motion • Simple Harmonic Motion • Energy of a Simple Harmonic Oscillator • The Pendulum • Comparing Simple Harmonic Motion and Uniform Circular Motion • Damped Oscillations • Forced Oscillations

Simple Harmonic Motion Hookes Law F = -kx F = restoring force x = displacement from equilibrium position

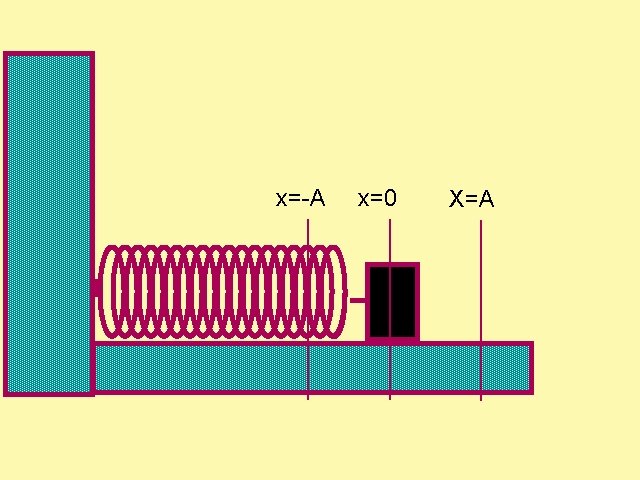
x=-A x=0 X=A

F( t ) - kx( t ) ma ( t ) m 2 Û d x dt 2 Differential Equation, - k m d 2 x dt 2 x need to find solution so that left hand side = right hand side From looking at graph of position versus time Guess: x ( t ) = Acos(w t); A and w constants.

What is the meaning of the constant A at time t = 0 x(0) = Acos(0) = A t =0 º the displacement from equilibrium at time p at time t = w æ pö x Acos w = Acos(p) = - A = è wø The max and min values ofx are ± A Û A is the amplitude of the motion º the maximum displacement from equilibrium positi

cos(x) +1 cos(2 n ) = +1 -1 cos([2 n+1] ) = -1

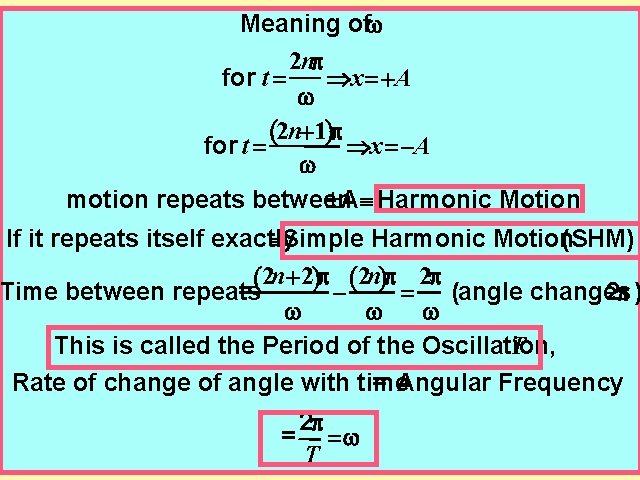
Meaning ofw 2 np for t Þx +A w 2 n+1)p ( for t Þx -A w motion repeats between ±AºHarmonic Motion If it repeats itself exactly (SHM) ºSimple Harmonic Motion 2 n+2)p (2 n)p 2 p ( Time between repeats = 2 p ) (angle changes w w w T This is called the Period of the Oscillation, Rate of change of angle with time = Angular Frequency 2 p = w T

The number of times motion repeats 1 insecond 1 w f T 2 p [ f] Hz º cps; rad º s- 1 [w ] s 2 p m T 2 p k w

2 np (2 n + 1)p ; t w w (t )v - A w sin (wt ) Þ at these times the velocity x ±AÛ t 2 np ö v æ - A sin æ w - A sin (2 np ) 0 è w ø è ø w æ (2 n + 1 )p ö v - A sin w - A sin ((2 n + 1) p ) 0 è ø w w so velocity is zero at maximum displacement the acceleration on the other hand is a maximum æ (2 n + 1)p ö æ 2 np ö 2 2 a A = -w A ; a w è w ø è ø w x 0 The acceleration is zero when x 0 The velocity is the greatest when v max ± Aw

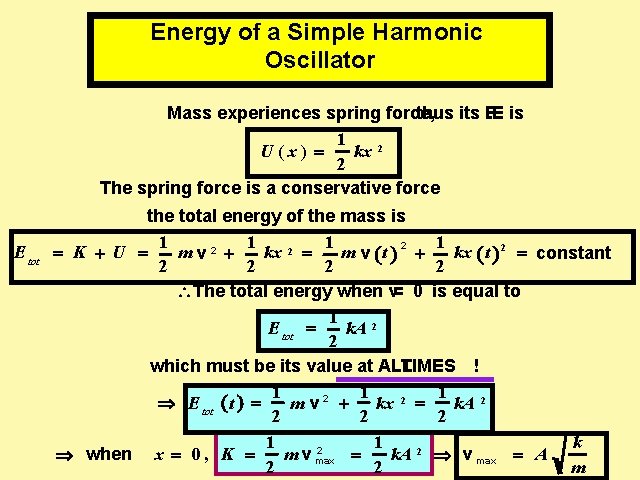
Energy of a Simple Harmonic Oscillator Mass experiences spring force, thus its P. E is 1 U ( x) kx 2 2 The spring force is a conservative force E tot the total energy of the mass is 1 1 2 mv 2 + kx 2 m v (t ) + kx ( t ) 2 constant K +U 2 2 The total energy when v= 0 is equal to 1 E tot k. A 2 2 which must be its value at ALL TIMES ! 1 1 1 m v 2 + kx 2 k. A 2 Þ E tot ( t ) 2 2 2 1 1 k 2 m v max k. A 2 Þ v max A Þ when x 0 , K 2 2 m

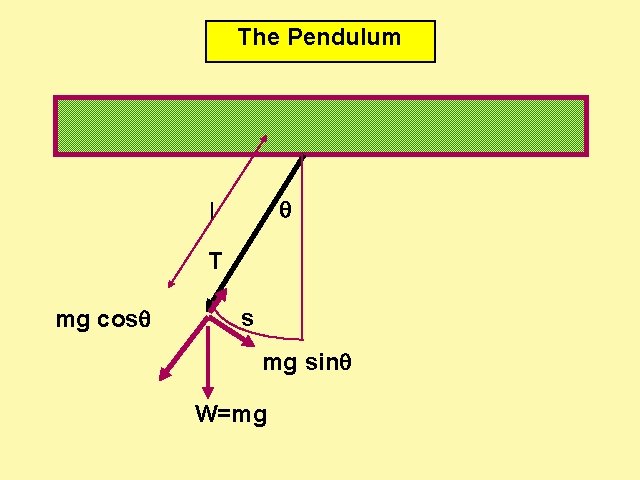
The Pendulum l T mg cos s mg sin W=mg

Force opposing motion F -mgsin » mg when is small s mg s F -mg l l º Hookes Law for the Pendulum d 2 s 2 , This force provides the tangential acceleration dt and we obtain a similar differential equation to before. Comparing to before we see mg k « & x «s l s(t ) Acos(wt ) T 2 p m ml l 2 p k mg g

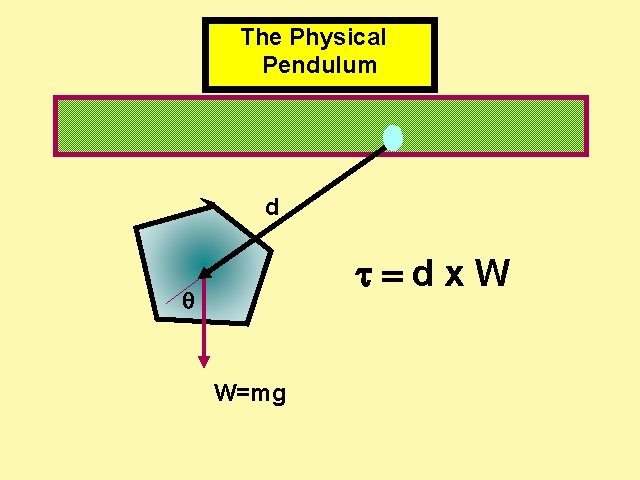
The Physical Pendulum d d x W W=mg

we formulate this more generally for an object suspended a distance d from its center of gravity by using angular quantities. Restoring torque(against motion ) due to gravity. ) = - mgd sin » -mgd (small angle approx using = Ia d 2 mgd Þa 2 -w 2 , where w = dt I Þ (t ) A cos (wt ) Þ T 2 p I mgd I

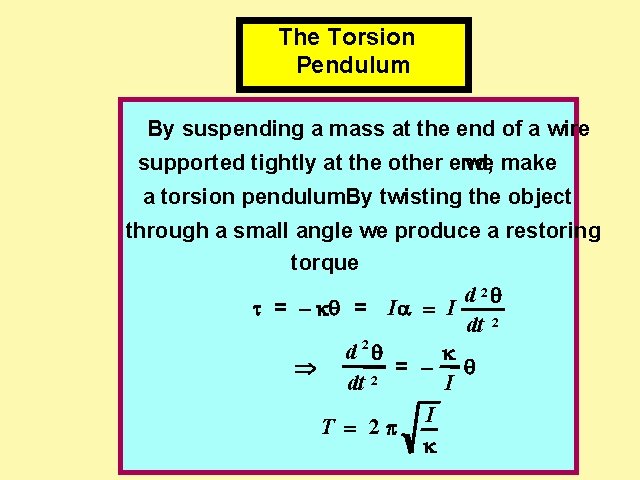
The Torsion Pendulum By suspending a mass at the end of a wire supported tightly at the other end, we make a torsion pendulum. By twisting the object through a small angle we produce a restoring torque d 2 = - k = Ia I dt 2 d 2 k = - Þ 2 dt I I T 2 p k

Comparing Simple Harmonic Motion and Uniform Circular Motion x( t ) Acos(wt ) is precisely the time variation of the x coordinate of a particle performing uniform circular motion about a fixed point , A. at a fixed distance æ p ö y( t ) Asin(wt ) = Acos wt is the time variation è ø 2 of the y coordinate, which is a SHM variation. p Here though we have a phase shift of j = 2 p The argument wt - is called the phase of the motion. 2

Damped Oscillations If there are frictional forces present DEtot Wnc < 0 Thus the total energy decreases, and becomes E(t) ¹ constant. a non constant function of time, 1 Þ E(t) k. A(t )2 2 Þ A(t ) decreases with time The differential equation describing the position of a particle undergoing damped SHM are of the form d 2 x dx m -kx - b 2 dt dt

Forced Oscillations If there is another external oscillating force acting on the object (in the direction of motion ) one says that the motion of the oscillator is forced by this external force, the differential equation describing such motion is d 2 x dx m 2 = -kx - b + F 0 cos (w t) dt dt

solutions to this equation give amplitudes of the form A(t) = F 0 {(w - w ) 2 2 0 m 2 ( + bw m , )} 2 w 0 is the frequency of the SHM(i. e. no friction and forcing oscillation) If b (friction) is small, then if w » w 0 the amplitude becomes larger and larger º RESONANCE