Physics 1710 Chapter 2 Motion in One DimensionII

Physics 1710 Chapter 2 Motion in One Dimension—II Galileo Galilei Linceo (1564 -1642) • Discourses and Mathematical Demonstrations Concerning the Two New Sciences (1638) at age 74! (four years before his death at 78)

Physics 1710 Chapter 2 Motion in One Dimension Galileo’s Ramp

Physics 1710 Chapter 2 Motion in One Dimension—II 1′ Lecture Under uniform acceleration ax : • Acceleration is constant (hence “uniform”): ax = constant (>0, =0, or <0) • Velocity changes linearly in time: vfinal = vinitial + ax t • Displacement increases quadratically with time: xfinal = xinitial+vinitial t + ½ ax t 2

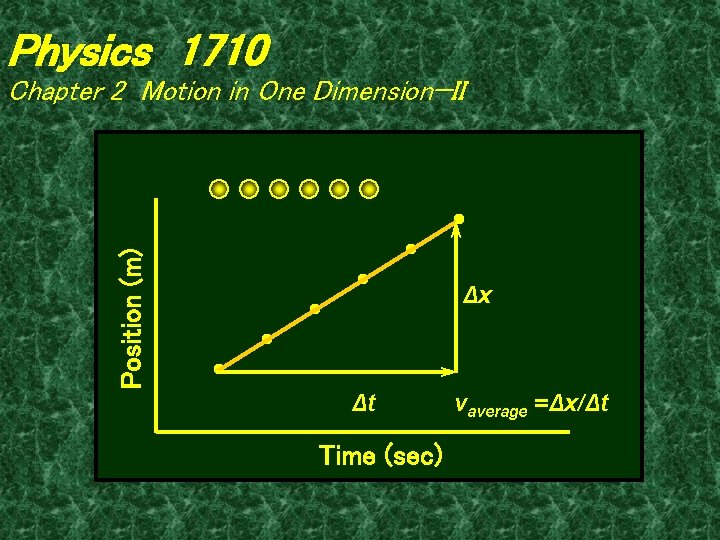
Physics 1710 Chapter 2 Motion in One Dimension—II Displacement is the change in position. Δx = xfinal - xinitial Δ is the change “operator”: Change in x = x at end – x at start ΔBalance = Balancefinal - Balanceinitial REVIEW

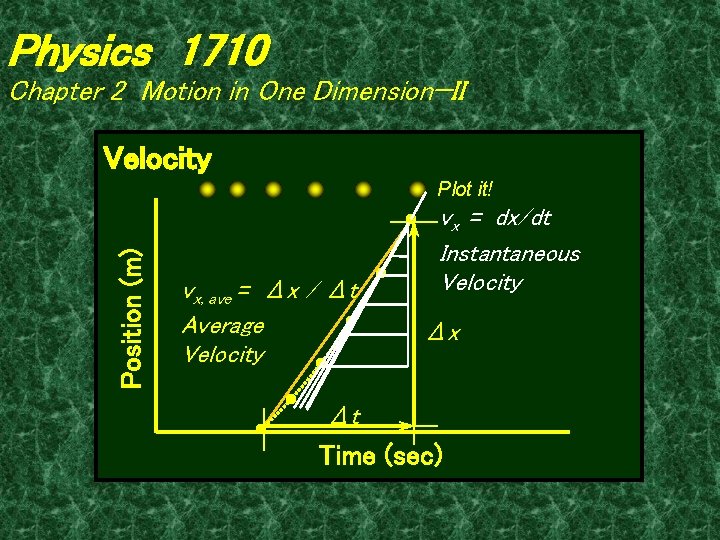
Physics 1710 Chapter 2 Motion in One Dimension—II Velocity is the time rate of displacement. Average velocity: vx, ave = Δ x / Δt Instantaneous velocity: vx = lim Δt→∞ Δx / Δt = dx/dt REVIEW

Physics 1710 Position (m) Chapter 2 Motion in One Dimension—II Δx Δt Time (sec) vaverage =Δx/Δt

Physics 1710 Chapter 2 Motion in One Dimension—II Velocity Position (m) Plot it! vx, ave = Δx / Δt Average Velocity vx = dx/dt Instantaneous Velocity Δx Δt Time (sec)

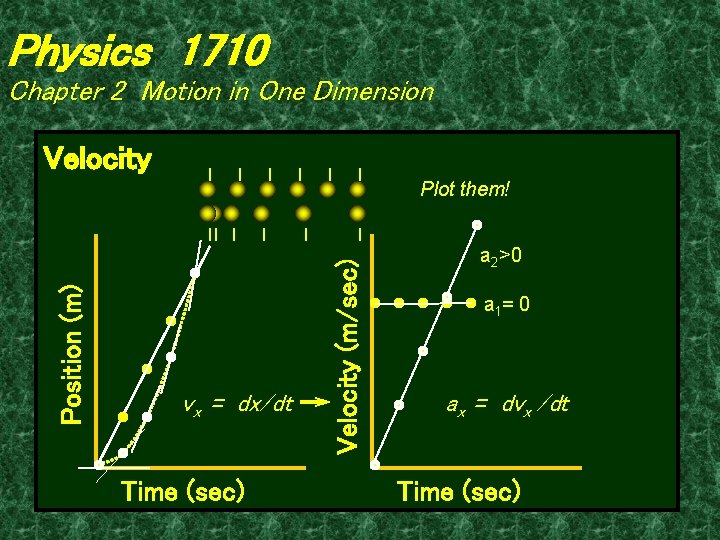
Physics 1710 Chapter 2 Motion in One Dimension—II Acceleration is the time rate of change of velocity. Average acceleration: ax, ave = Δvx / Δt = (vx, final -vx, initial )/ Δt Instantaneous acceleration: ax = lim Δt→∞ Δvx / Δt = dvx /dt ax = dvx /dt =d(dxx /dt)/dt = d 2 x/dt 2

Physics 1710 Chapter 2 Motion in One Dimension—II Motion Map From “snap shots” of motion at equal intervals of time we can determine the displacement, the average velocity and the average acceleration in each case. Uniform motion Accelerated motion

Physics 1710 Chapter 2 Motion in One Dimension Velocity vx = dx/dt Time (sec) Velocity (m/sec) Position (m) Plot them! a 2>0 a 1 = 0 ax = dvx /dt Time (sec)

Physics 1710 Chapter 2 Motion in One Dimension—II Galileo Galilei Linceo

Physics 1710 Chapter 2 Motion in One Dimension—II Galileo’s rule of odd numbers: Under uniform acceleration from rest, a body will traverse distances in successive equal intervals of time that stand in ratio as the odd numbers 1, 3, 5, 7, 9 …

Physics 1710 Chapter 2 Motion in One Dimension—II Galileo’s Ramp Demonstration

Physics 1710 Chapter 2 Motion in One Dimension—II Observation: 0 1 2 3 4 5 6 : : : : 0=02 0+1 =1 = 1 2 1+3 = 4 = 2 2 4+5 = 9 = 3 2 9+7= 16 = 4 2 16+9= 25 = 5 2 25+11= 36 = 6 2 ∆x ∝ t 2 ; from rest (vinitial = 0)

Physics 1710 Chapter 2 Motion in One Dimension—II Kinematic Equations from Calculus: (dv/dt) = a = constant ∫ 0 t (dv/dt) dt = ∫ 0 t a dt ∫vinitialvfinal dv = a (t-0) ∆v = v– vinitial = at The change in the instantaneous velocity is equal to the (constant) acceleration multiplied by its duration. v= vinitial + at

Physics 1710 Chapter 2 Motion in One Dimension—II Kinematic Equations from Calculus: dx/dt = v ∫ 0 t (dx/dt) dt = ∫ 0 t v dt x – xinitial = ∫ 0 t (vinitial + at) dt = vinitial (t-0) + ½ a(t 2 -0) ∆x = vinitial t + ½ at 2 The displacement under uniform acceleration is equal to the displacement at constant velocity plus one half the acceleration multiplied by the square of its duration. x = xinitial + vinitial t + ½ at 2

Physics 1710 Chapter 2 Motion in One Dimension—II Kinematic Equations from Calculus: v 2 = (vinitial + at) 2 v 2 = vinitial 2 +2 vinitial at + a 2 t 2 v 2 = vinitial 2 + 2 a (vinitial t + ½ at 2) v 2 = vinitial 2 +2 a∆x The change in the square of the velocity is equal to two times the acceleration multiplied by the distance over which the acceleration is applied.

Physics 1710 Chapter 2 Motion in One Dimension—II 80/20 facts: Kinematic Equations (1 -D Uniform a): vx final = vx initial + ax t x final = x initial + vx initial t + ½ axt 2 vx final 2 = vx initial 2 + 2 ax (x final - x initial )

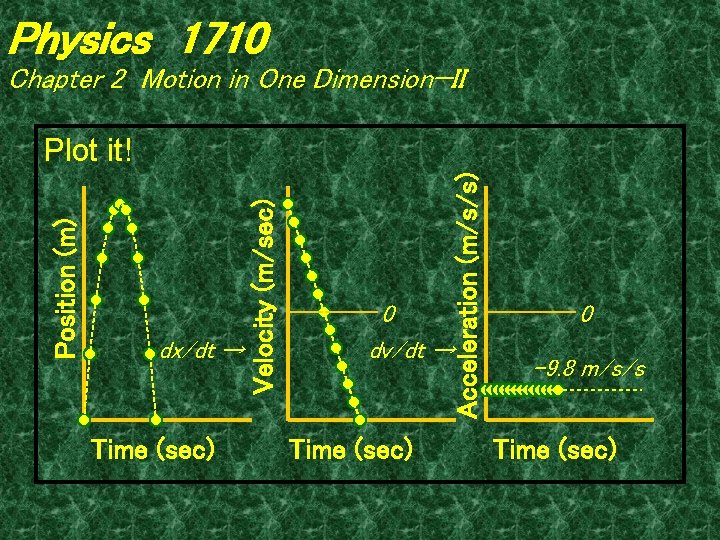
Physics 1710 Chapter 2 Motion in One Dimension—II 80/20 facts: In free fall near the Earth, all bodies are accelerated uniformly downward with an acceleration of az = - g = -9. 80 m/s 2.

Physics 1710 Chapter 2 Motion in One Dimension—II Time (sec) Acceleration (m/s/s) dx/dt → Velocity (m/sec) Position (m) Plot it! 0 dv/dt → Time (sec) 0 -9. 8 m/s/s Time (sec)

Physics 1710 Chapter 2 Motion in One Dimension—II Summary: • The change in the instantaneous velocity is equal to the (constant) acceleration multiplied by its duration. ∆v = at • The displacement is equal to the displacement at constant velocity plus one half of the product of the acceleration and the square of its duration. ∆x = vinitial t + ½ at 2 • The change in the square of the velocity is equal to two times the acceleration multiplied by the distance traveled during acceleration. ∆v 2 = 2 a ∆x • The acceleration of falling bodies is 9. 8 m/s/s downward. a = - g = - 9. 8 m/s/s

Physics 1710 Chapter 2 Motion in One Dimension—II 1′ Essay: One of the following: • The main point of today’s lecture. • A realization I had today. • A question I have.