Physics 151 Principles of Physics Mechanics Heat Honors

Physics 151: Principles of Physics: Mechanics & Heat (Honors) Prof. Stan Zygmunt Neils 142 464 -5380

Road Map for the Semester • • • Kinematics (2 weeks) Newtonian Mechanics (2 weeks) Conservation Laws (6 weeks) Gravitation (1 week) Thermal Physics (3 weeks)

I. 1 -D Motion A. Average and Instantaneous Velocity B. Average and Instantaneous Acceleration C. 1 -D Motion with Constant Acceleration D. Bodies in Free-Fall Near the Earth’s Surface E. Approximation Techniques

A. Average and Instantaneous Velocity Definitions for a particle moving along the x-axis (1 -D): Average velocity Instantaneous velocity Graphical meaning: slope of x(t) graph Derivative of x with respect to time

B. Average and Instantaneous Acceleration Similarly we define: Average acceleration Instantaneous acceleration Graphical meaning: slope of v(t) graph Derivative of v with respect to time

C. 1 -D Motion with Constant Acceleration General expression: Now integrating both sides from 0 to time t: Now if acceleration is constant: or: Graphical meaning: area under a(t) graph

We can repeat this procedure to find x(t): General expression: Now integrating both sides from 0 to time t: Which for constant acceleration gives: Combining these two results gives several other useful equations!

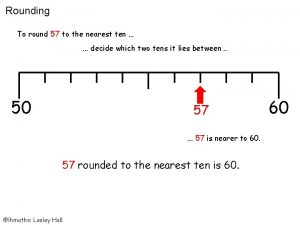
Kinematic Equations for 1 -D Constant Acceleration Motion 1. 2. 3. 4. Solve for t in (1) and plug into (2) Solve for a in (1) and plug into (2)

D. Bodies in Vertical Free Fall Near the Earth 1. 2. 3. 4.

Example With Two Moving Objects Two identical stones are initially atop a cliff 43. 9 m above the water. The first one is dropped from rest, while the second stone is thrown downward 1. 0 s later. The two stones hit the water at the same time. Find the initial velocity of the second stone. Problem-Solving Steps: 1 & 2. Draw a diagram and choose a coordinate system. 3. Write down the known quantities using kinematic symbols. 4. Write equations for the unknown quantity in term of the known quantities. 5 & 6. Solve for the unknown quantity and check your answer.

Measuring g The acceleration of gravity can be measured by launching an object vertically and measuring the time it takes the object to pass two given points A and B: TB B h TA A Find an expression for g in terms of h, TA, and TB.

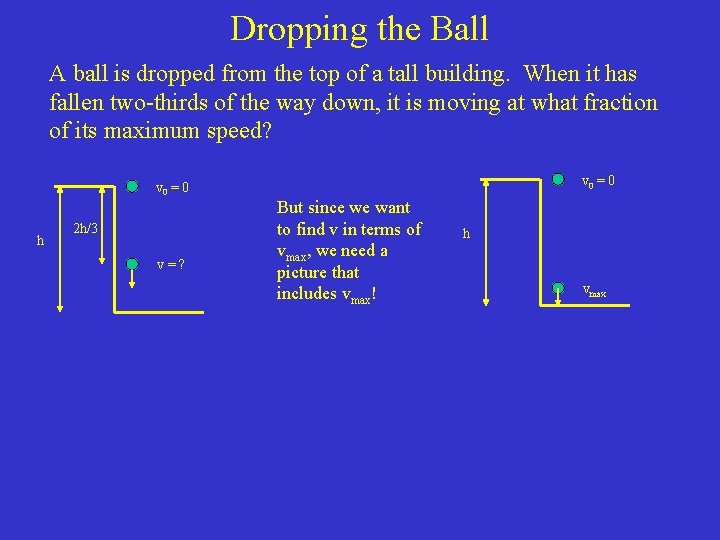
Dropping the Ball A ball is dropped from the top of a tall building. When it has fallen two-thirds of the way down, it is moving at what fraction of its maximum speed? v 0 = 0 h 2 h/3 v=? v 0 = 0 But since we want to find v in terms of vmax, we need a picture that includes vmax! h vmax

E. Approximation Techniques Often in physics we will be able to obtain a result in analytical form (i. e. , with symbols but no numerical values) but still wish to check to see if it makes sense. One good way to do this is to examine several limiting cases (for which we DO know the expected results) and find the approximate expression in each limiting case. To do this we need to use approximate formulas for mathematical functions that commonly arise in physics.

Useful Taylor Series Approximation Formulas Binomial Expansion: The usefulness of these can be seen when x << 1. Since each term has successively higher powers of x, each term will be (much) smaller than the previous term. Thus just a few terms (maybe just two!) will provide a very good approximation.

An example: Let’s say we want to find the gravitational potential energy U for the system of a thin rod of mass M 1 and length L and a sphere of mass M 2, when they are oriented as shown below: M 1 r M 2 L Later in the fall semester you will learn how to use calculus to find the result: But how (beyond checking the dimensions) can we tell if this is correct?

How to check this answer: We know what to expect if the two objects are a long way apart, because in that case their respective sizes will not matter and their potential energy will be approximately that of two point particles separated by a distance r: So we should examine our exact result to see if it approximately agrees with the expected result when L << r. To do this, we rewrite our exact result:

Now notice that if L << r, the second term in parentheses is much smaller than 1, so we can use the Taylor Series expansion to write: based on: This gives the approximate result: Which agrees with the expected result for a large separation! This agreement, while not proving that our exact answer is correct, gives us a great deal of confidence in it.

Another example: Assume we know the force on an object as a function of its xcoordinate: where a and b are constants Let’s find the approximate expression for the force valid when the x-coordinate is much larger than a (x >> a). To do this, we will need to rewrite the expression for F and use the binomial expansion equation:

Here are the steps: No approximations have be made so far. But now note that we can write: where This allows us to use to obtain