Physics 111 Lecture 03 Motion in Two Dimensions

Physics 111 Lecture 03 Motion in Two Dimensions SJ 8 th Ed. : Ch. 4. 1 – 4. 4 • • 4. 1 4. 2 4. 3 4. 4 4. 5 4. 6 Position, velocity, acceleration vectors Average & Instantaneous Velocity Average & Instantaneous Acceleration Two Dimensional Motion with Constant Acceleration (Kinematics) Projectile Motion (Free Fall) Uniform Circular Motion Tangential and Radial Acceleration Relative Velocity and Relative Acceleration Position, Velocity and Acceleration Vectors Two Dimensional Motion with Constant Acceleration Projectile Motion A particle in Uniform Circular Motion Tangential and Radial Acceleration Relative Velocity and Relative Acceleration Copyright R. Janow – Spring 2012

Motion in two and Three Dimensions Extend 1 dimensional kinematics to 2 D and 3 D • Kinematic quantities become 3 dimensional • Vectors needed to manipulate quantities • Motions in the 3 perpendicular directions can be analyzed independently • Constant acceleration Kinematic Equations hold component-wise for each dimension Same for z • In vector notation each equation is 3 separate ones for x, y, z Copyright R. Janow – Spring 2012

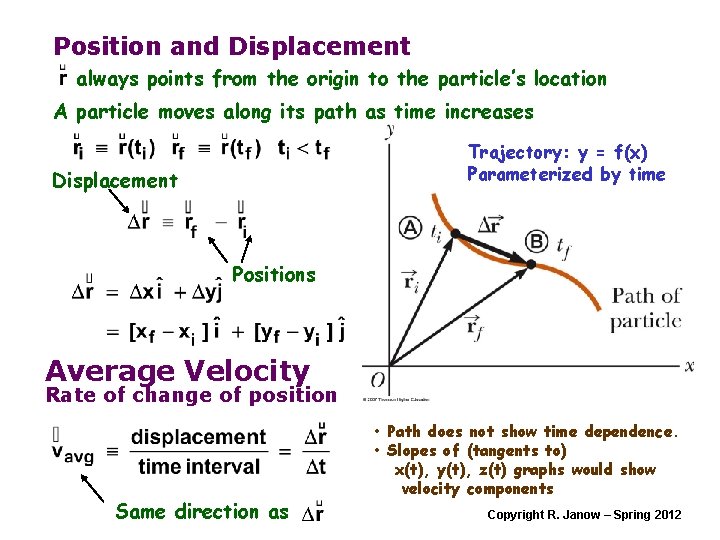
Position and Displacement always points from the origin to the particle’s location A particle moves along its path as time increases Trajectory: y = f(x) Parameterized by time Displacement Positions Average Velocity Rate of change of position Same direction as • Path does not show time dependence. • Slopes of (tangents to) x(t), y(t), z(t) graphs would show velocity components Copyright R. Janow – Spring 2012

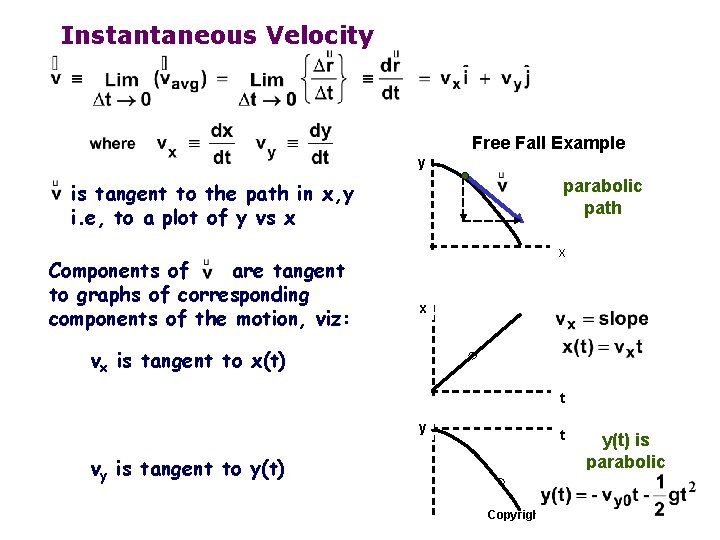
Instantaneous Velocity Free Fall Example y parabolic path is tangent to the path in x, y i. e, to a plot of y vs x Components of are tangent to graphs of corresponding components of the motion, viz: x x vx is tangent to x(t) t y vy is tangent to y(t) t y(t) is parabolic Copyright R. Janow – Spring 2012

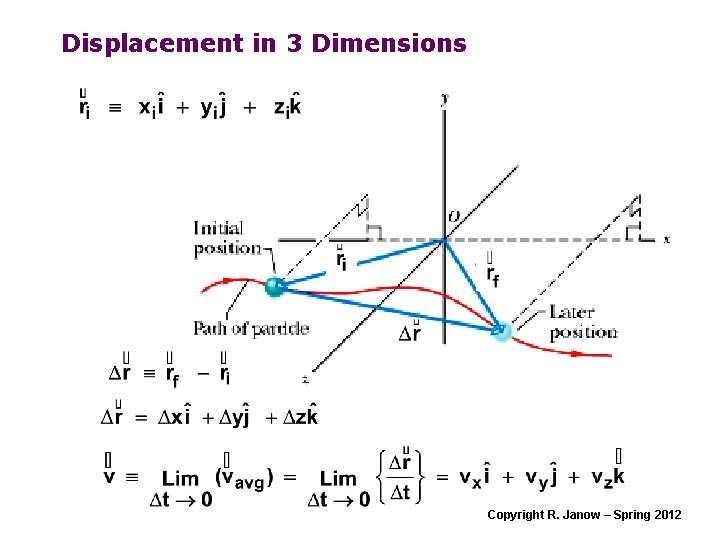
Displacement in 3 Dimensions Copyright R. Janow – Spring 2012

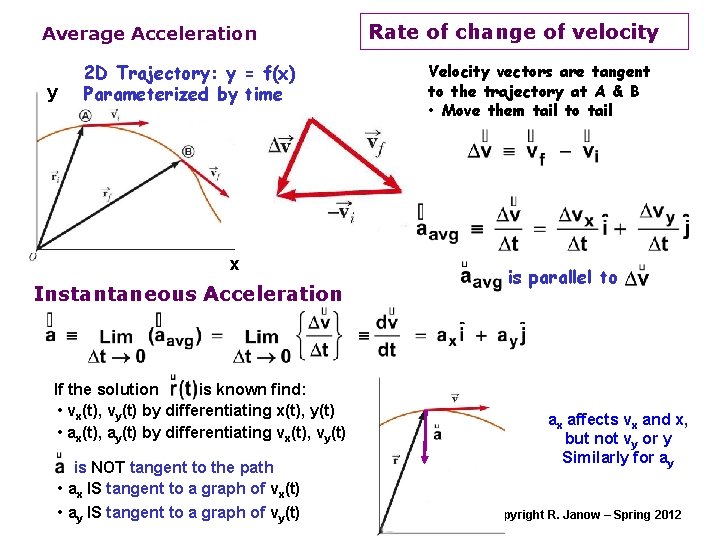
Average Acceleration y 2 D Trajectory: y = f(x) Parameterized by time x Instantaneous Acceleration If the solution is known find: • vx(t), vy(t) by differentiating x(t), y(t) • ax(t), ay(t) by differentiating vx(t), vy(t) is NOT tangent to the path • ax IS tangent to a graph of vx(t) • ay IS tangent to a graph of vy(t) Rate of change of velocity Velocity vectors are tangent to the trajectory at A & B • Move them tail to tail is parallel to ax affects vx and x, but not vy or y Similarly for ay Copyright R. Janow – Spring 2012

Summary – 3 D Kinematics Formulas Definitions: Vector Form - Motion with Constant Acceleration - 2 D or 3 D PARABOLAS Easiest to use in Cartesian coordinates – The x, y, z, dimensions move independently - Choose ax, ay, az and initial conditions independently Cartesian Scalar Form - Constant Acceleration Same for z Copyright R. Janow – Spring 2012

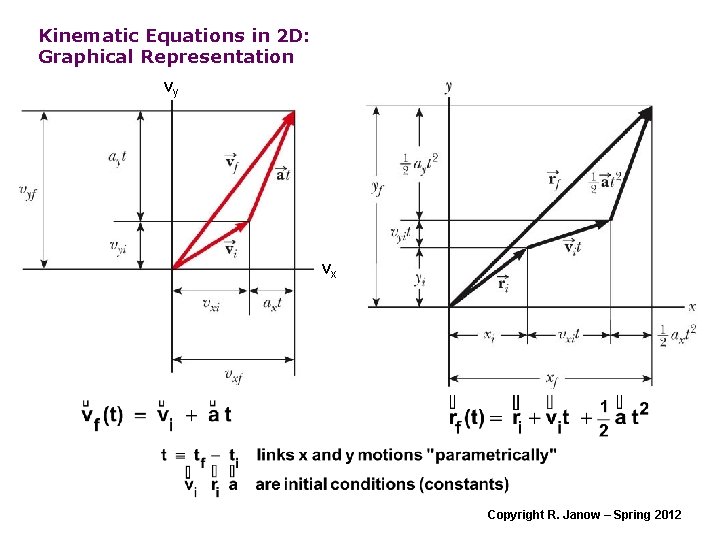
Kinematic Equations in 2 D: Graphical Representation vy vx Copyright R. Janow – Spring 2012

Projectile Motion: Motion of a particle under constant, downward gravitation only Assume: • Free fall along y direction (up/down) with horizontal motion as well ay = constant = - g, ax, az = 0 Velocity in x-z direction is constant. • Trajectory (a parabola) lies in a plane. Can choose it to be x-y. Motion is 2 D, not 3 D. • Usually pick initial location at origin: x 0 = 0, y 0 = 0 at t=0 • Initial conditions: § v 0 has x and y components vx 0 = v 0 cos(q), vy 0 = v 0 sin(q) § vx is constant, no drag or non-gravitation forces usually § If vx = 0, motion is strictly vertical, range = 0 path y Equations: No acceleration along x Acceleration = - g along y v 0 y q v 0 x x Copyright R. Janow – Spring 2012

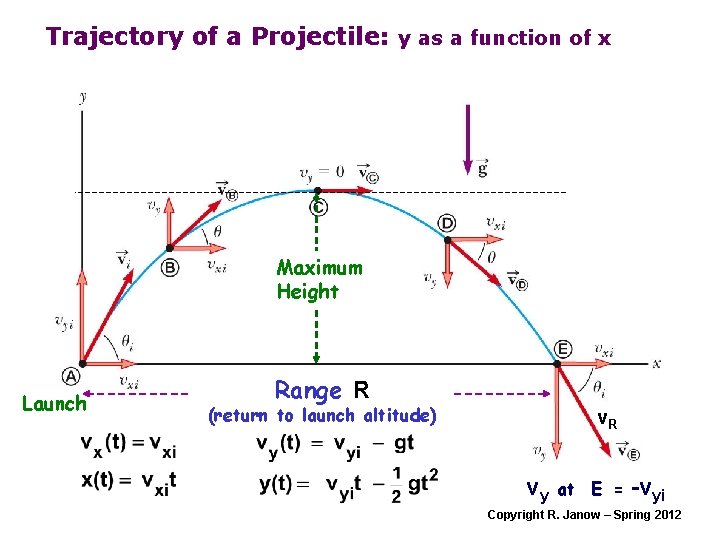
Trajectory of a Projectile: y as a function of x Maximum Height Launch Range R (return to launch altitude) v. R vy at E = -vyi Copyright R. Janow – Spring 2012

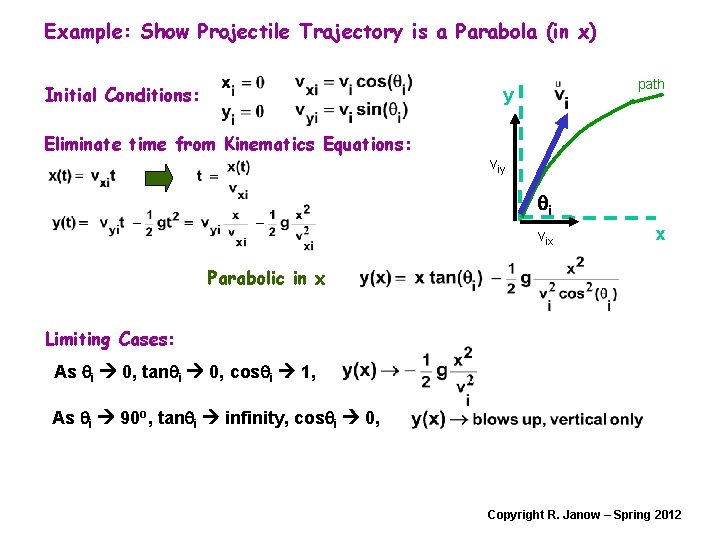
Example: Show Projectile Trajectory is a Parabola (in x) Initial Conditions: path y Eliminate time from Kinematics Equations: viy qi vix x Parabolic in x Limiting Cases: As qi 0, tanqi 0, cosqi 1, As qi 90 o, tanqi infinity, cosqi 0, Copyright R. Janow – Spring 2012

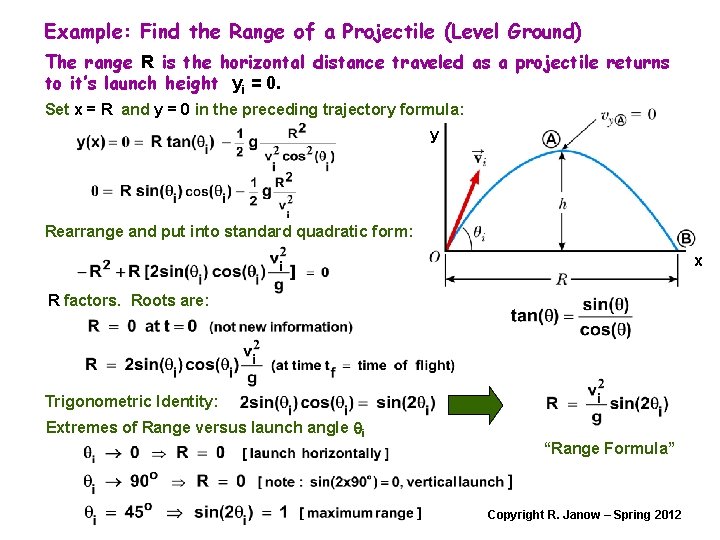
Example: Find the Range of a Projectile (Level Ground) The range R is the horizontal distance traveled as a projectile returns to it’s launch height yi = 0. Set x = R and y = 0 in the preceding trajectory formula: y Rearrange and put into standard quadratic form: x R factors. Roots are: Trigonometric Identity: Extremes of Range versus launch angle qi “Range Formula” Copyright R. Janow – Spring 2012

Example: Time of Flight for a Projectile Find the time of flight t. R for range R – the time to return to the original launch height yi = 0. Set y = 0 in the y-displacement formula: This is a quadratic equation in t. R – factor it: The roots are: and: Find speed vf at time t. R - passing y = 0 on the way down vxf = vxi = vicos(qi) (constant) qi = qf Find maximum height ymax reached at time tmax Same speed at the same altitude Set vy, max = 0 at tmax Copyright R. Janow – Spring 2012

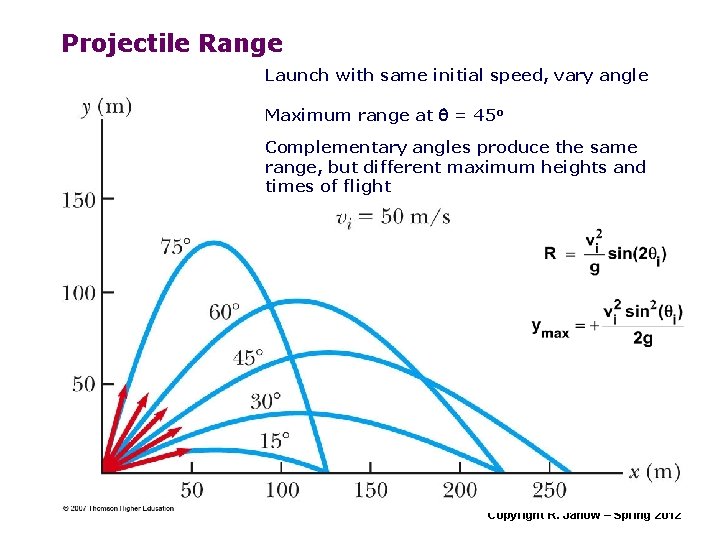
Projectile Range Launch with same initial speed, vary angle Maximum range at q = 45 o Complementary angles produce the same range, but different maximum heights and times of flight Copyright R. Janow – Spring 2012

Problem Solving Strategy Text (page 43) defines a general 4 step method: • • Conceptualize Categorize Analyze Finalize Additional problem solving hints for mechanics: • Choose coordinate system(s). Try to make choices that simplify representing the problem. For example, where acceleration a is constant try choosing an axis along the direction of a. • Make a sketch showing axes, origin, particles. • Choose names for the important quantities that will help you remember what they mean. Be sure to distinguish quantities of the same type, such as v, vx, vy, vi, vf, …. • List the known quantities and the given initial conditions, like vxi, vyi, ax, ay, … Show these on your sketch. • Choose equations to use for describing the motion in the problem. Time connects the x, y, z dimensions and is sometimes to be eliminated via algebra. Copyright R. Janow – Spring 2012

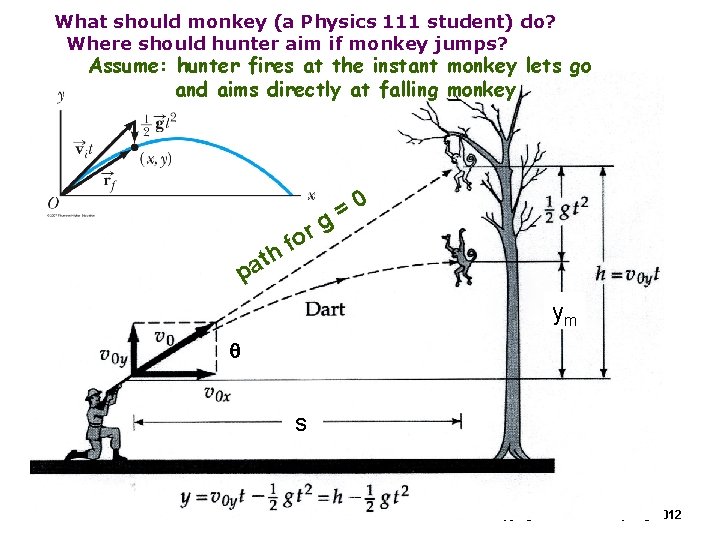
What should monkey (a Physics 111 student) do? Where should hunter aim if monkey jumps? Assume: hunter fires at the instant monkey lets go and aims directly at falling monkey or f h 0 = g t a p ym q xsm Copyright R. Janow – Spring 2012

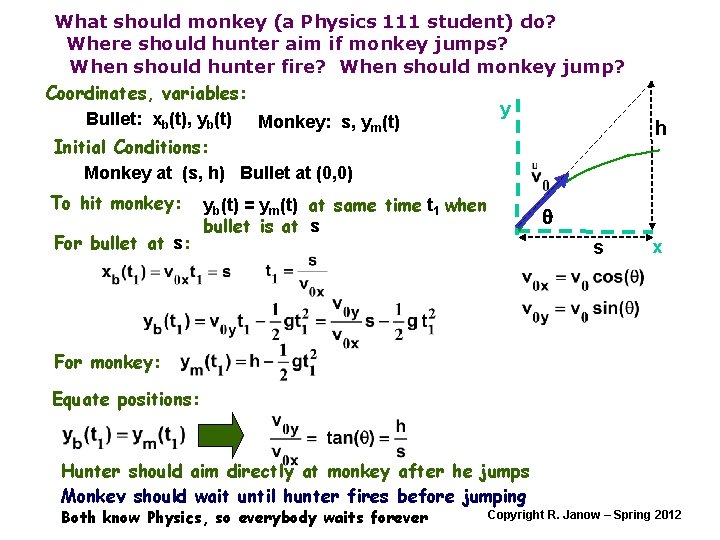
What should monkey (a Physics 111 student) do? Where should hunter aim if monkey jumps? When should hunter fire? When should monkey jump? Coordinates, variables: y Bullet: xb(t), yb(t) Monkey: s, ym(t) Initial Conditions: Monkey at (s, h) Bullet at (0, 0) To hit monkey: For bullet at s: yb(t) = ym(t) at same time t 1 when bullet is at s h q s x For monkey: Equate positions: Hunter should aim directly at monkey after he jumps Monkey should wait until hunter fires before jumping Both know Physics, so everybody waits forever Copyright R. Janow – Spring 2012

Example: Find the arrow’s speed An arrow is shot horizontally by a person whose height is not known. It strikes the ground 33 m away horizontally, making an angle of 86 o with the vertical. What was the arrow’s speed as it was released? v 0 R = v 0 t t = R / v 0 R = 33 m vf t = flight time = time to hit ground 86 o Final velocity components: No acceleration along x Vy 0 = 0, t as above Divide equations to eliminate vf: Rearrange: Copyright R. Janow – Spring 2012

Uniform Circular Motion • A particle in Uniform Circular Motion moves in a circular path with a constant speed The radius vector is rotating. • The velocity vector is always tangent to the particle’s path (as usual). It is perpendicular to the (rotating) radius vector. • The particle is accelerating, since the direction of the velocity is constantly changing. • The centripetal acceleration vector always points toward the center of the circle. • The magnitudes of all three vectors are constant, but their directions are changing • All three vectors are rotating with the same constant angular velocity and period. • The period of revolution T is: • The frequency f is the reciprocal of the period f = 1/T Copyright R. Janow – Spring 2012

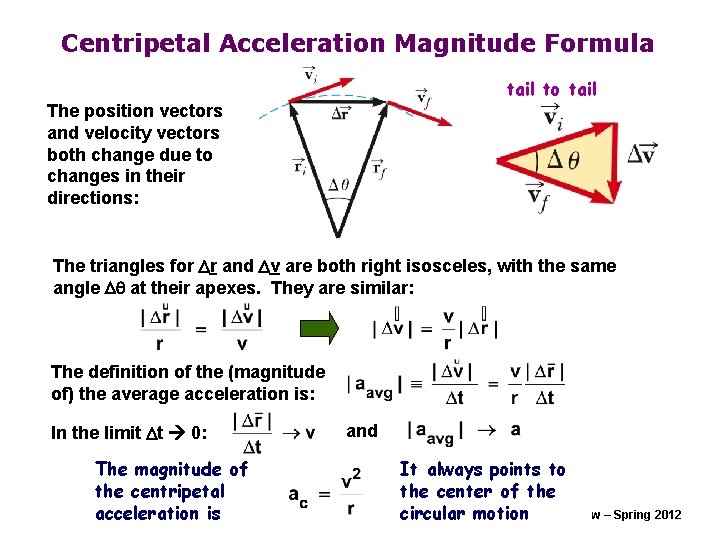
Centripetal Acceleration Magnitude Formula tail to tail The position vectors and velocity vectors both change due to changes in their directions: The triangles for Dr and Dv are both right isosceles, with the same angle Dq at their apexes. They are similar: The definition of the (magnitude of) the average acceleration is: In the limit Dt 0: The magnitude of the centripetal acceleration is and It always points to the center of the circular motion Copyright R. Janow – Spring 2012

Example: Find the Earth’s centripetal acceleration in its orbit about the Sun Assume uniform circular motion The radius of the Earth’s orbit is r = 1. 5 x 1011 m Need to find the speed v T = 1 year = 365 X 24 x 3600 s = 3. 156 x 107 s Example: Need to find the speed v Passengers on an amusement park ride move in circles whose radius is 5 m. They complete a full circle every 4 seconds. What acceleration do they feel, in “g”s”? dimensionless Copyright R. Janow – Spring 2012

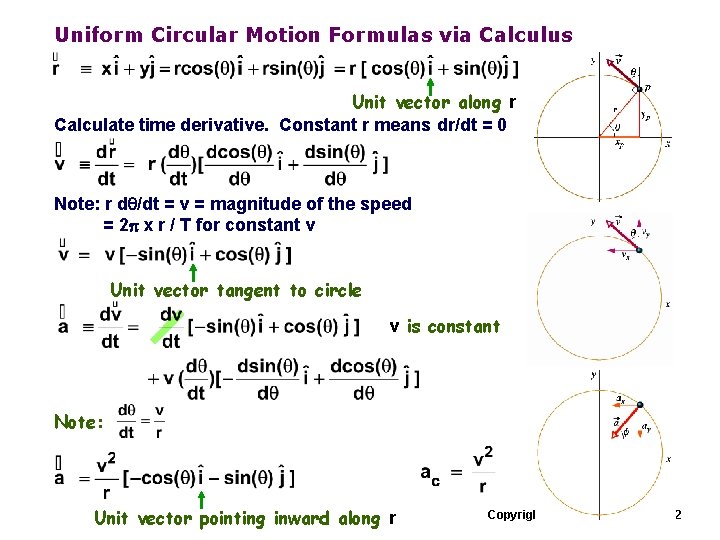
Uniform Circular Motion Formulas via Calculus Unit vector along r Calculate time derivative. Constant r means dr/dt = 0 Note: r dq/dt = v = magnitude of the speed = 2 p x r / T for constant v Unit vector tangent to circle v is constant Note: Unit vector pointing inward along r Copyright R. Janow – Spring 2012