PHYSICS 11 TODAY Vectors and Displacement CHAPTER 1

PHYSICS 11 TODAY: • Vectors and Displacement

CHAPTER 1. 4 Vectors and Displacement

Displacement and Vectors

1 – D and 2 – D MOTION One dimensional motion is the simplest form of motion Example: A train can go only in one dimension forward – backward along the tracks

FRAME of REFERENCE Think about the train…. . What about the motion around the train? ? ? Earth is spinning on its axis , so the train must be spinning with Earth

FRAME of REFERENCE Think about the train…. . What about the motion around the train? ? ? At the same time, Earth is spinning, around the sun, and so is the train

FRAME of REFERENCE Think about the train…. . What about the motion around the train? ? ? At the same time, the sun and the rest of solar system is moving through our galaxy

FRAME of REFERENCE We choose a reference point at a specific time and place against which we will measure changes in position of the train To think about the train’s motion, WE MUST MAKE THINGS SIMPLER!

FRAME of REFERENCE We choose a reference point at a specific time and place against which we will measure changes in position of the train It is called…

FRAME of REFERENCE A system for specifying the precise location of an object in space and time STATION 1 For example: a departing station along the train’s route might be a great frame of reference

DISPLACEMENT As an object moves from one position to another, the length of the straight line drawn from its initial to the final position is called:

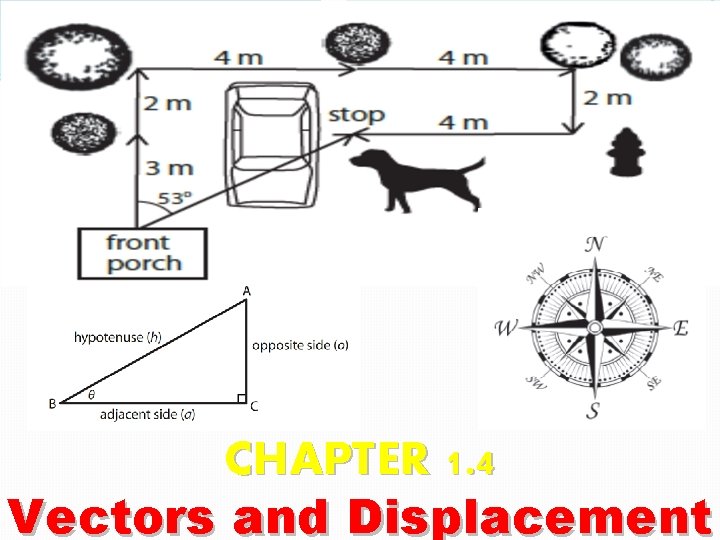
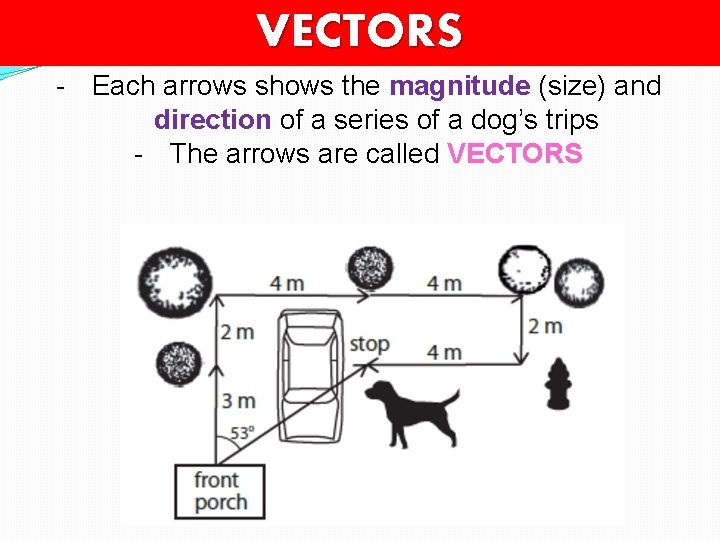
VECTORS - Each arrows shows the magnitude (size) and direction of a series of a dog’s trips - The arrows are called VECTORS

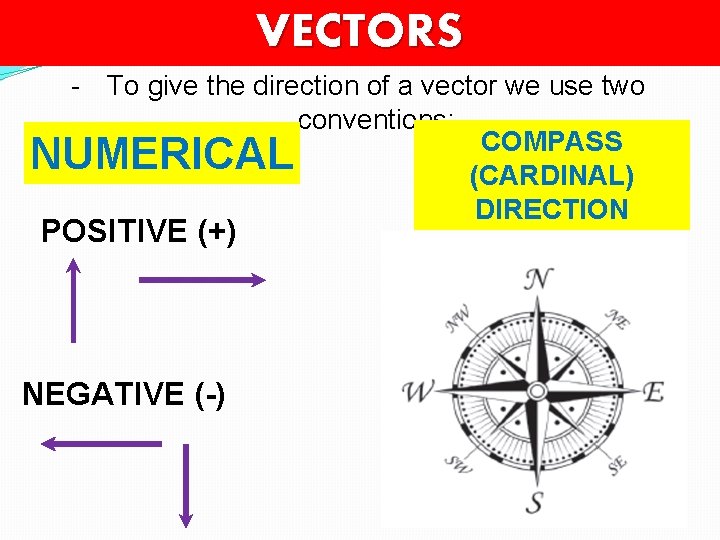
VECTORS - To give the direction of a vector we use two conventions: COMPASS NUMERICAL (CARDINAL) DIRECTION POSITIVE (+) NEGATIVE (-)

TREASURE HUNTING WITH VECTORS

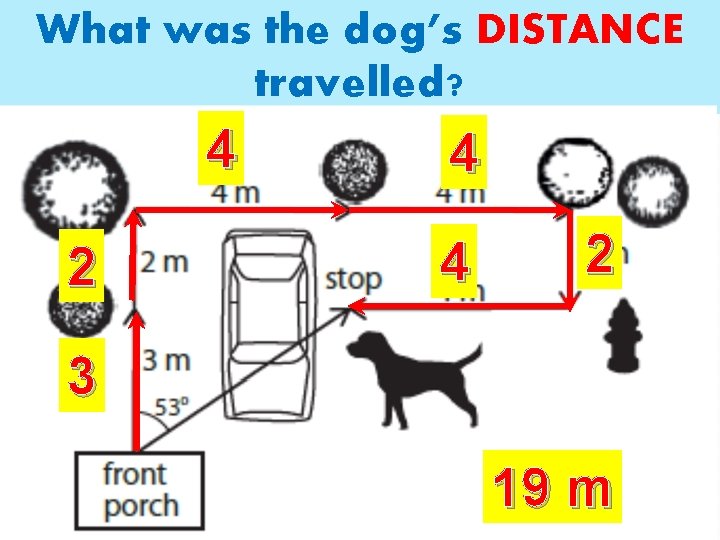
What was the dog’s DISTANCE travelled? 4 2 4 4 2 3 19 m

What was the dog’s DISPLACEMENT? ? ?

Conceptual Challenge A space shuttle takes off from Florida and circles Earth several times, finally landing in Los Angeles. While the shuttle is in flight, a movie star flies from Los Angeles to Florida to shoot a movie.

Conceptual Challenge A space shuttle takes off from Florida and circles Earth several times, finally landing in Los Angeles. While the shuttle is in flight, a movie star flies from Los Angeles to Florida to shoot a movie. Who undergoes the greater displacement, the movie star or a space shuttle? What is the difference between the displacements?

Displacement = distance travelled? ? A space shuttle takes off from Florida and circles Earth several times, finally landing in Los Angeles. While the shuttle is in flight, a movie star flies from Los Angeles to Florida to shoot a movie. Who travelled a greater distance?

DISPLACEMENT What is the geckos' displacement?

DISPLACEMENT What if I changed zero on the meter stick to the gecko’s initial position? What would be its displacement then?

Displacement vs Distance WORLD MAP Homework!!

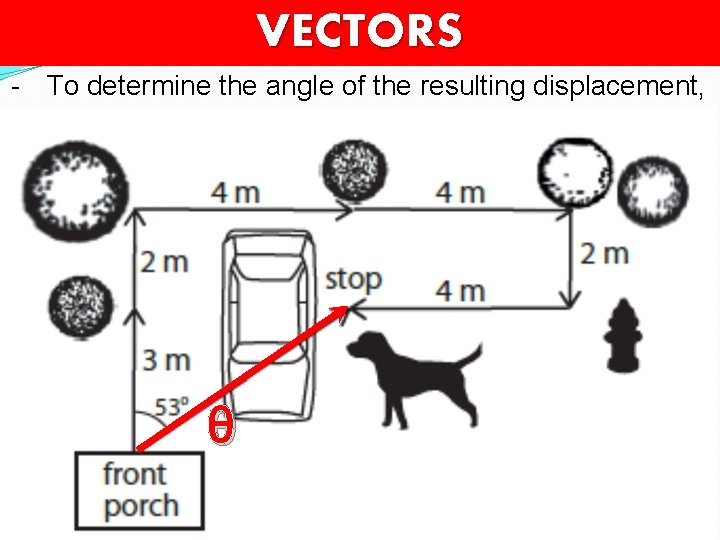
VECTORS - To determine the angle of the resulting displacement, θ

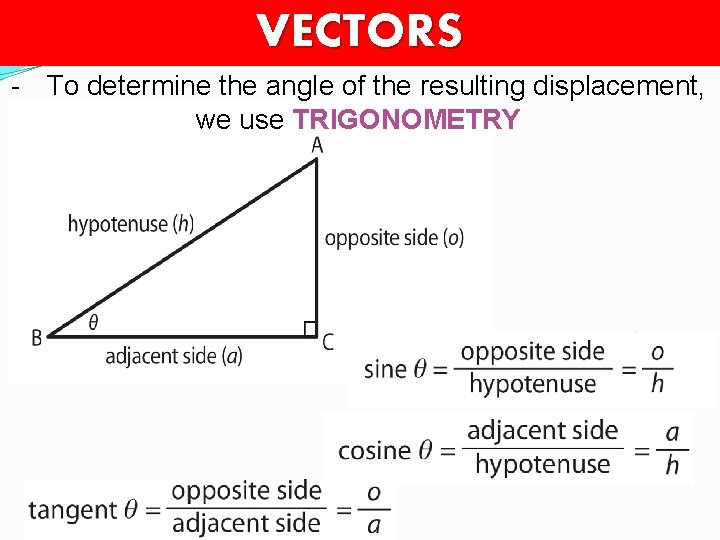
VECTORS - To determine the angle of the resulting displacement, we use TRIGONOMETRY

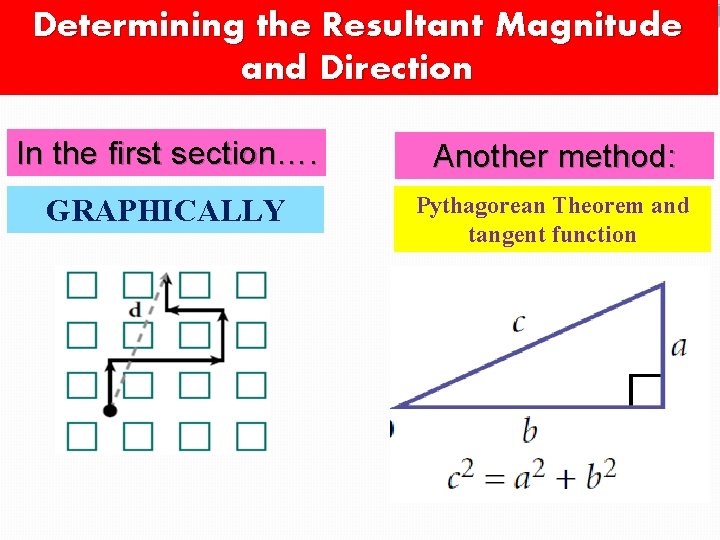
Determining the Resultant Magnitude and Direction In the first section…. Another method: GRAPHICALLY Pythagorean Theorem and tangent function

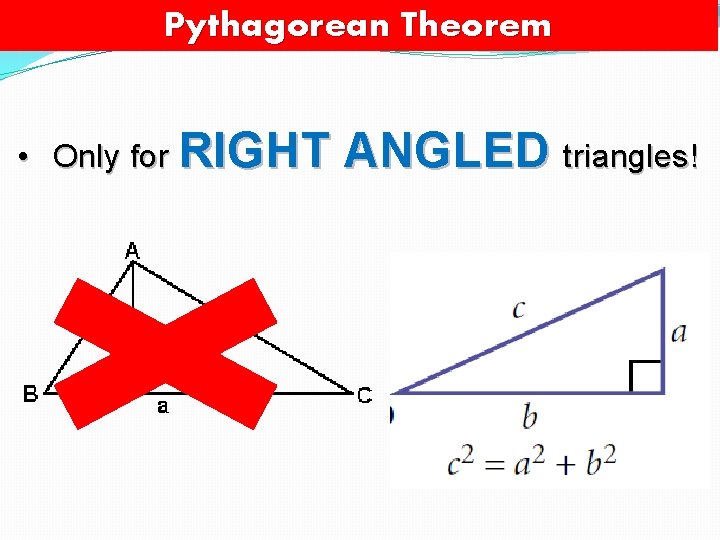
Pythagorean Theorem • Only for RIGHT ANGLED triangles!

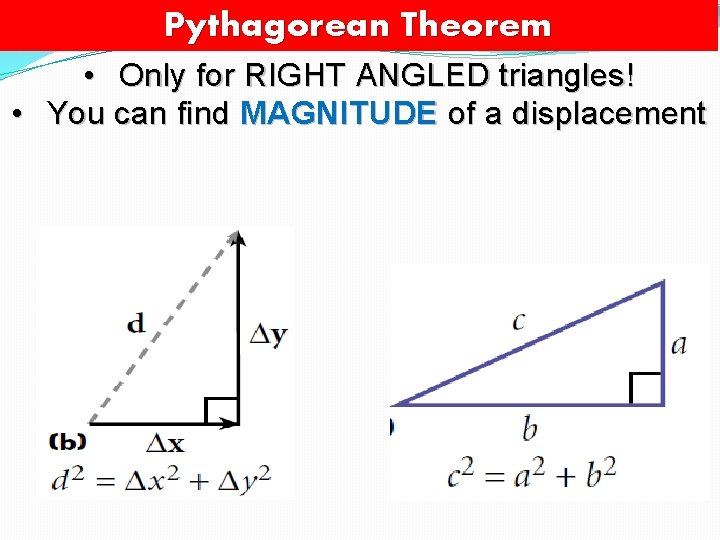
Pythagorean Theorem • Only for RIGHT ANGLED triangles! • You can find MAGNITUDE of a displacement

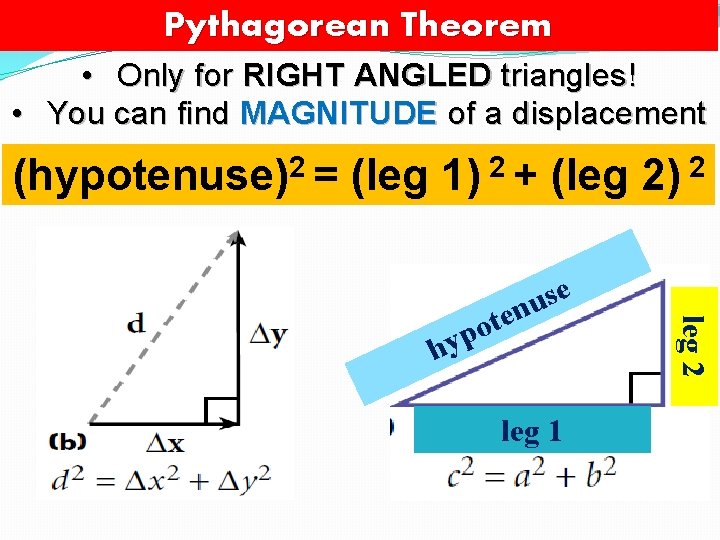
Pythagorean Theorem • Only for RIGHT ANGLED triangles! • You can find MAGNITUDE of a displacement (hypotenuse)2 = (leg 1) 2 + (leg 2) 2 leg 1 leg 2 h t o yp e s u en

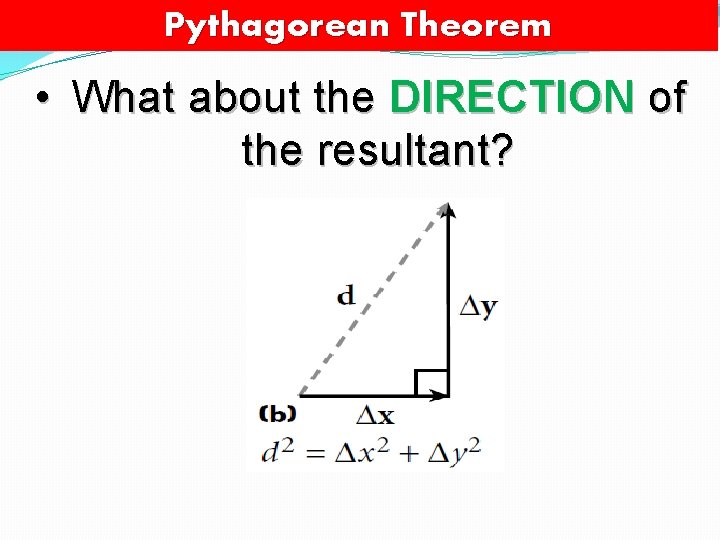
Pythagorean Theorem • What about the DIRECTION of the resultant?

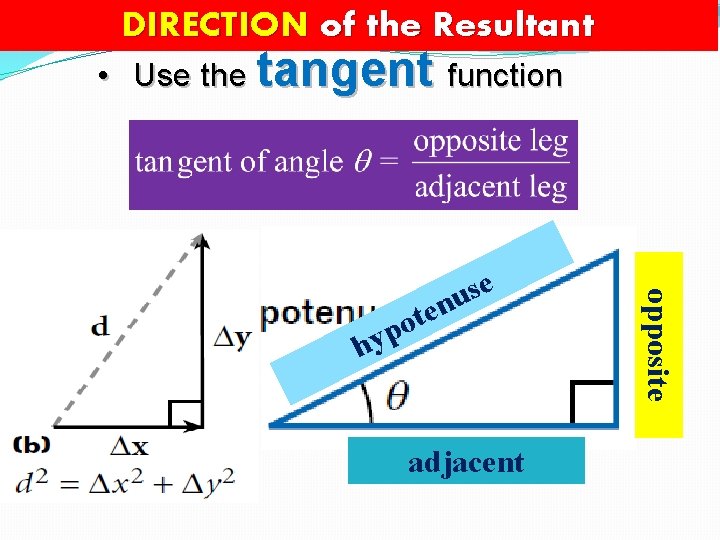
DIRECTION of the Resultant • Use the tangent function t o p y h adjacent opposite e s enu

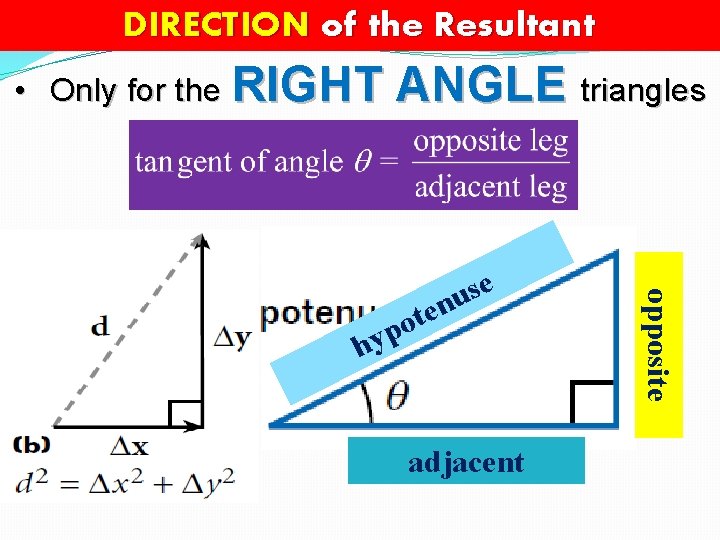
DIRECTION of the Resultant • Only for the RIGHT ANGLE triangles t o p y h adjacent opposite e s enu

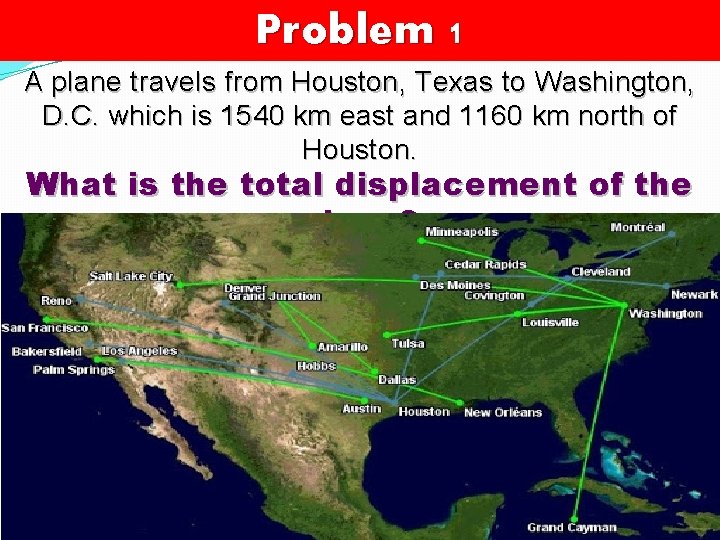
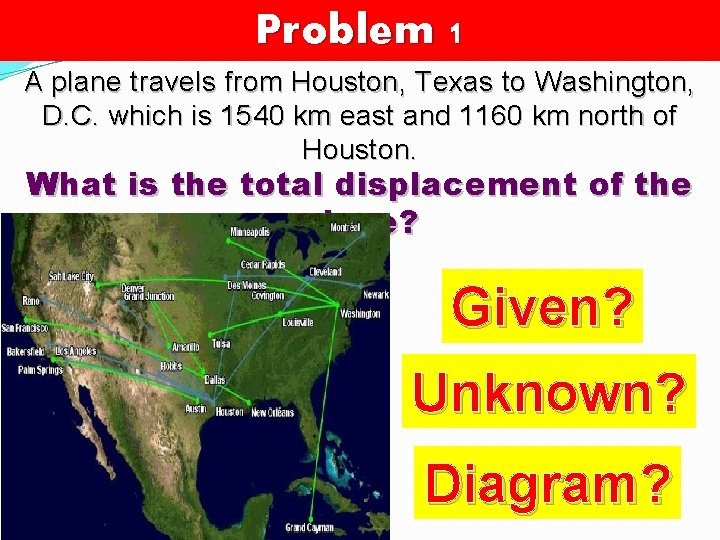
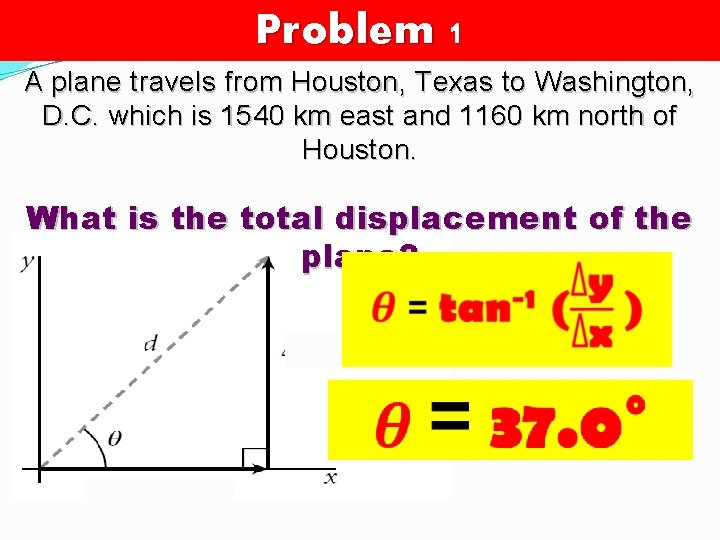
Problem 1 A plane travels from Houston, Texas to Washington, D. C. which is 1540 km east and 1160 km north of Houston. What is the total displacement of the plane?

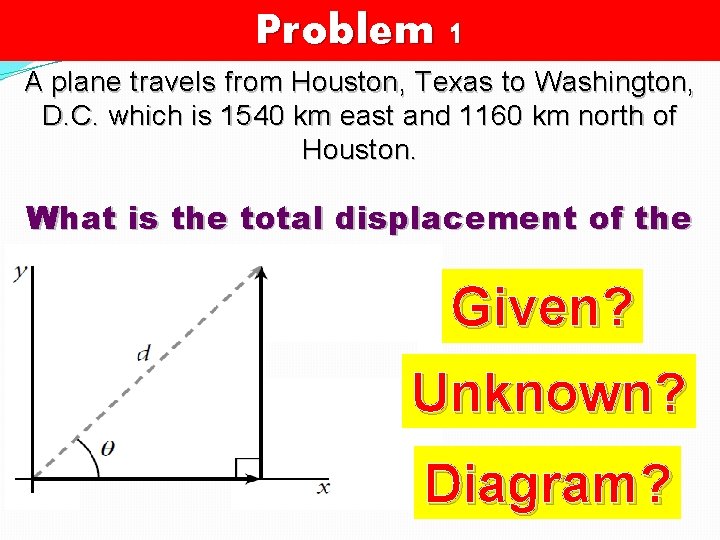
Problem 1 A plane travels from Houston, Texas to Washington, D. C. which is 1540 km east and 1160 km north of Houston. What is the total displacement of the plane? Given? Unknown? Diagram?

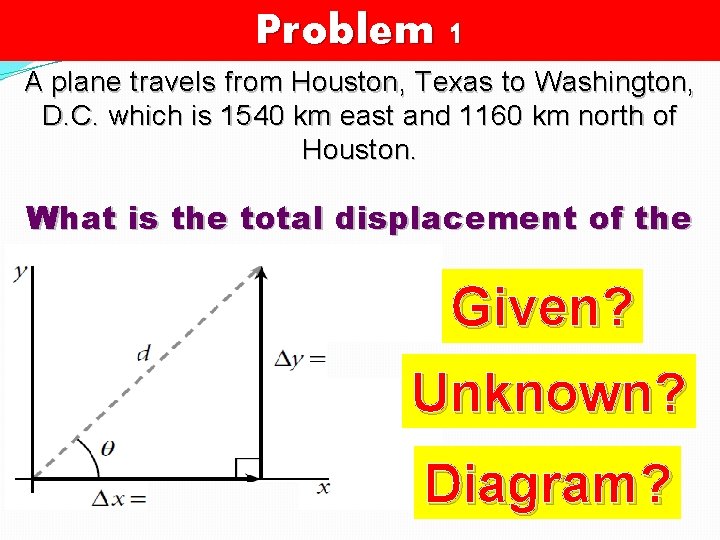
Problem 1 A plane travels from Houston, Texas to Washington, D. C. which is 1540 km east and 1160 km north of Houston. What is the total displacement of the plane? Given? Unknown? Diagram?

Problem 1 A plane travels from Houston, Texas to Washington, D. C. which is 1540 km east and 1160 km north of Houston. What is the total displacement of the plane? Given? Unknown? Diagram?

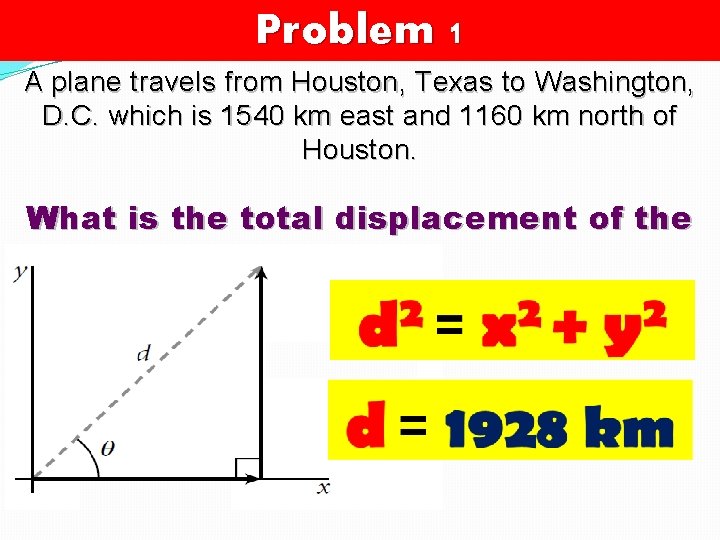
Problem 1 A plane travels from Houston, Texas to Washington, D. C. which is 1540 km east and 1160 km north of Houston. What is the total displacement of the plane?

Problem 1 A plane travels from Houston, Texas to Washington, D. C. which is 1540 km east and 1160 km north of Houston. What is the total displacement of the plane?

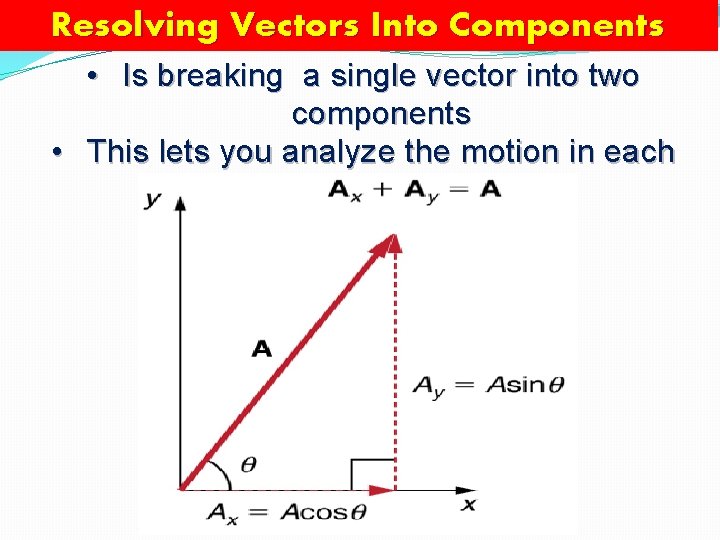
Resolving Vectors Into Components • Is breaking a single vector into two components • This lets you analyze the motion in each direction: X and Y

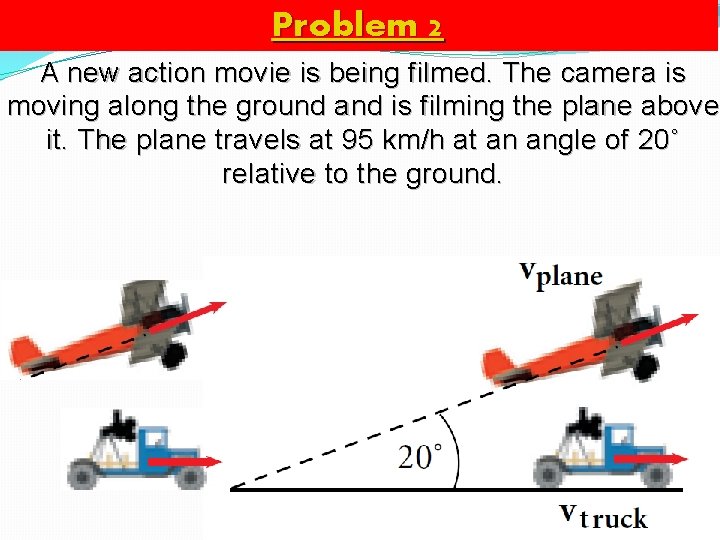
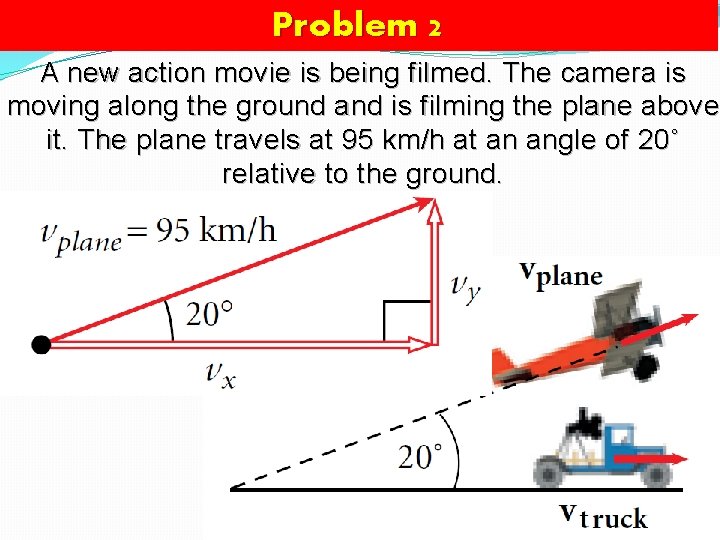
Problem 2 A new action movie is being filmed. The camera is moving along the ground and is filming the plane above it. The plane travels at 95 km/h at an angle of 20˚ relative to the ground. What is the velocity that the car must maintain in order to stay underneath the plane?

Problem 2 A new action movie is being filmed. The camera is moving along the ground and is filming the plane above it. The plane travels at 95 km/h at an angle of 20˚ relative to the ground.

Problem 2 A new action movie is being filmed. The camera is moving along the ground and is filming the plane above it. The plane travels at 95 km/h at an angle of 20˚ relative to the ground.

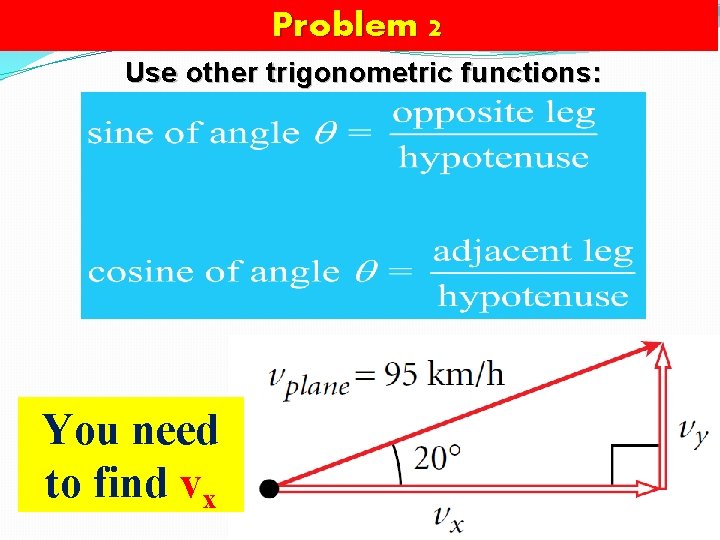
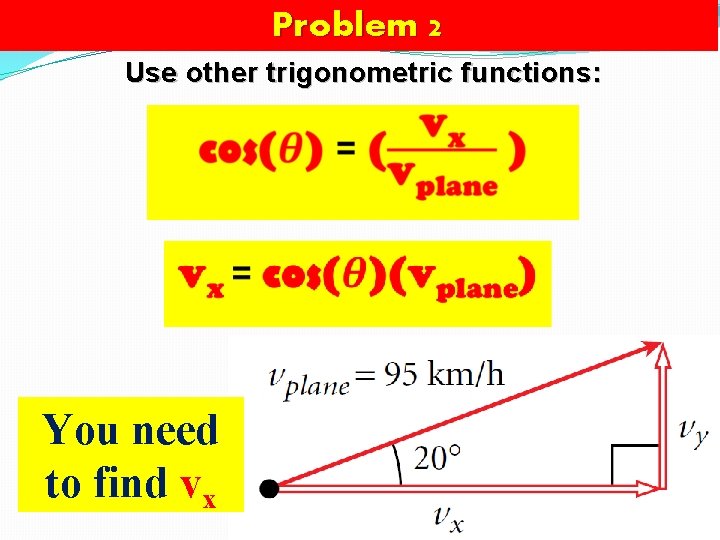
Problem 2 Use other trigonometric functions: You need to find vx

Problem 2 Use other trigonometric functions: You need to find vx

Problem 2 Use other trigonometric functions: You need to find vx

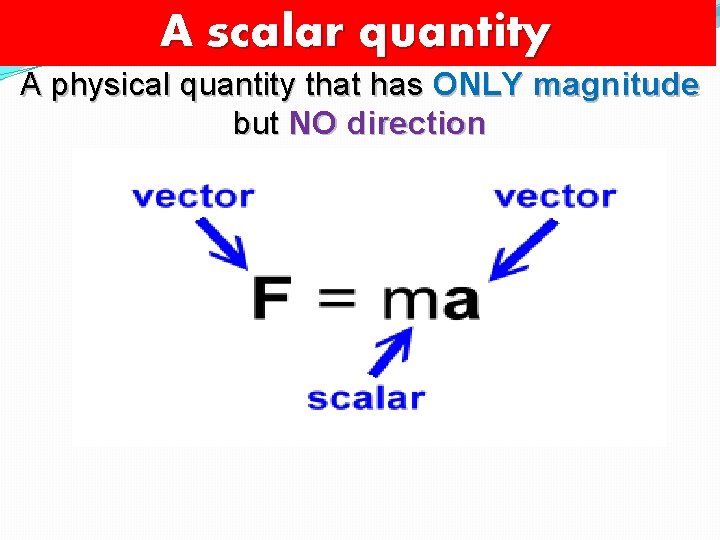
Scalar Quantities vs. Vector Quantities Scalars Vectors Have magnitude (size) Have No direction Have Direction

A scalar quantity A physical quantity that has ONLY magnitude but NO direction

A vector quantity A physical quantity that has both, magnitude and one direction

What scalars and vectors do you know? Scalars Length Area Volume Speed Density Mass Pressure Temperature Energy Entropy Work Power Vectors Displacement Direction Velocity Acceleration Force Momentum Lift Drag Thrust Tension Weight

Representation of Vectors 1. In your textbook: 2. In HW, quizzes, or tests: speed velocity

Representation of Vectors Use a diagram with arrows: 1. Arrows point to the direction of the vector 2. The length of an arrow represents the magnitude

Representation of Vectors Why do we consider velocity instead of speed in order to decide which player reaches the ball first? Direction is important because a player can run very fast but not towrds the ball

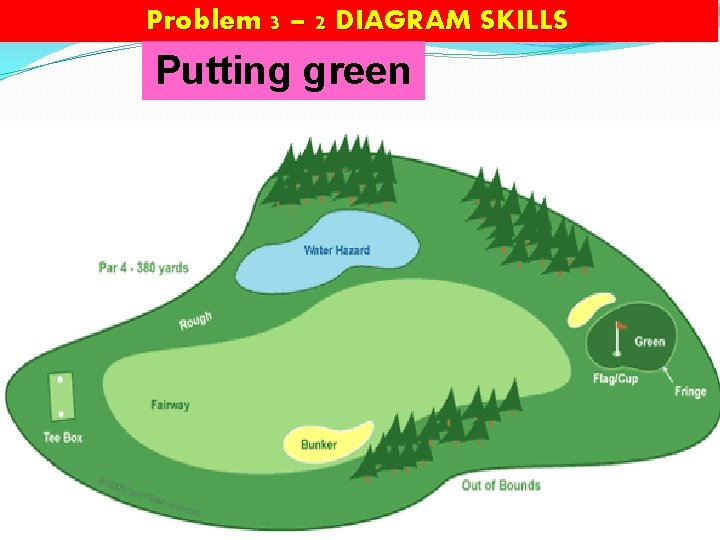
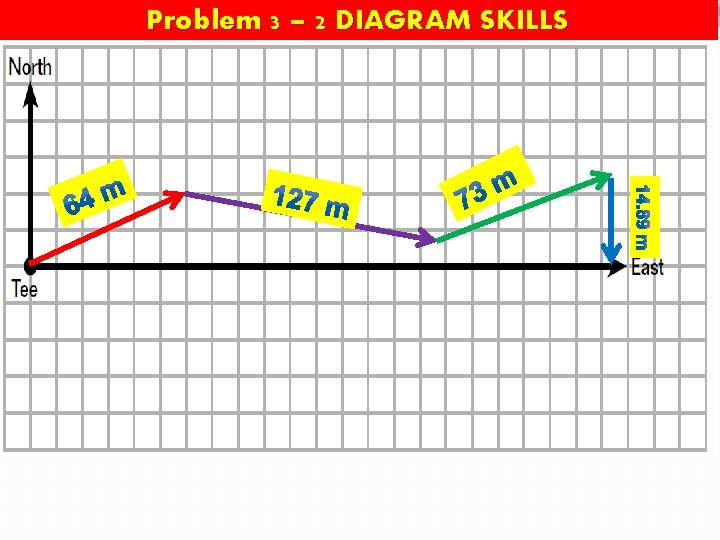
Problem 3 – 2 DIAGRAM SKILLS Sand trap Tee shot

Problem 3 – 2 DIAGRAM SKILLS Putting green

Problem 3 – 2 DIAGRAM SKILLS

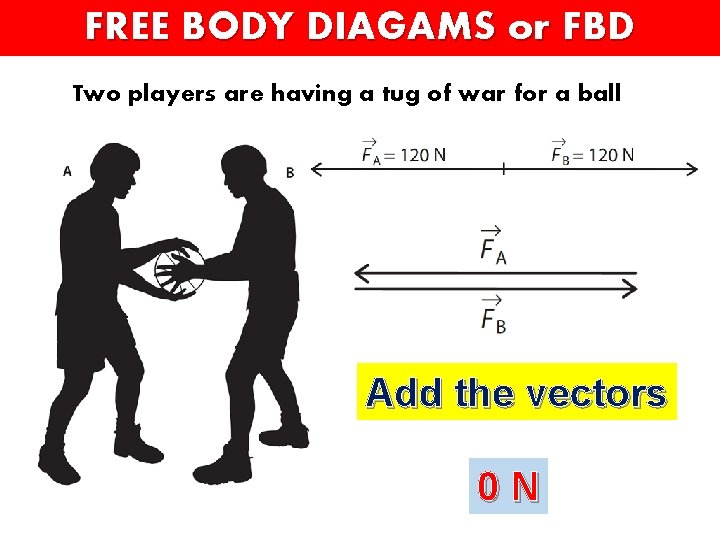
FREE BODY DIAGAMS or FBD Two players are having a tug of war for a ball • Player A is pulling with a force of 120. 0 N to the left • Player B is pulling with a force of 120. 0 N to the right Add the vectors The answer…

FREE BODY DIAGAMS or FBD Two players are having a tug of war for a ball Add the vectors 0 N

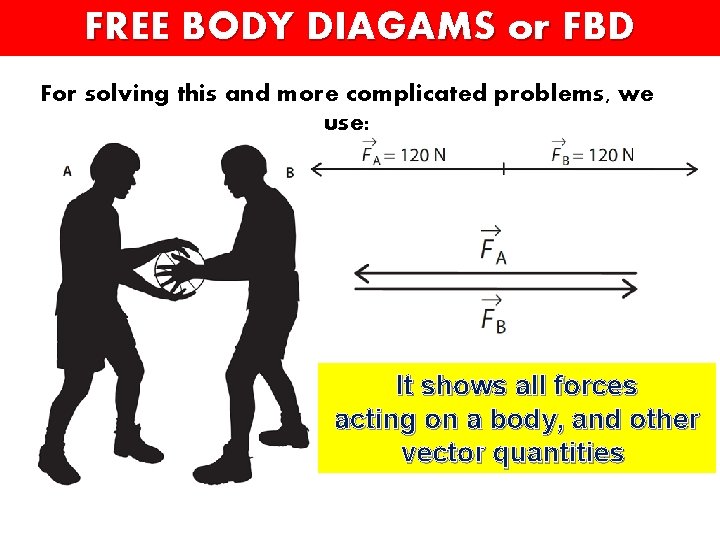
FREE BODY DIAGAMS or FBD For solving this and more complicated problems, we use: It shows all forces acting on a body, and other vector quantities

Worksheets on Vectors Operations