Physically Based Rendering Rendering that accurately reproduces the


Physically Based Rendering • Rendering that accurately reproduces the physical behavior of light – Laws of physics that represent the behavior of light (electromagnetic waves) • Geometrical Optics • Wave Optics – Wave Equation » Maxwell’s equations – Scattering Equation » Compton scattering » Rayleigh scattering » Mie scattering » Raman scattering » Etc…

Equation covered in this talk • The Rendering Equation – Equation that represents the light behavior in CG Rendering • was introduced by [Kajiya 86] • takes into account elements of geometrical optics • Ignores elements of wave optics – – – Volumetric rendering Sub-surface scattering Fluorescent effects Interference effects Etc…

Motivation • Achieve physically correct rendering by solving the rendering equation – Apologies in advance for the ton of equations • The goal of this talk is not about vaguely implementing functions and equations in the rendering field • It is about physically understanding them Caution! For ease of comprehension, in the slides, the w (outgoing direction) and w'(incident direction) are not written with positive or negative signs. When implementing these formulas, replace them by the right ones.

The Rendering Equation The equation that calculates Lo (outgoing light at direction w) from a given point x Different functions can be defined for each wavelength λ with different physical properties What does this equation represent?

Outgoing light Radiance outgoing to the direction w at given position x Radiance?

Radiance • F(radiant flux), the quantity of light that passes through an area on a unit sphere dw (solid angle) and a unit surface area d. A

Irradiance • F (radiant flux) incident on a unit area d. A

Radiant flux • Time derivative of the light energy – W (watt) = J/s – Q represents the light energy (radiant energy; J)
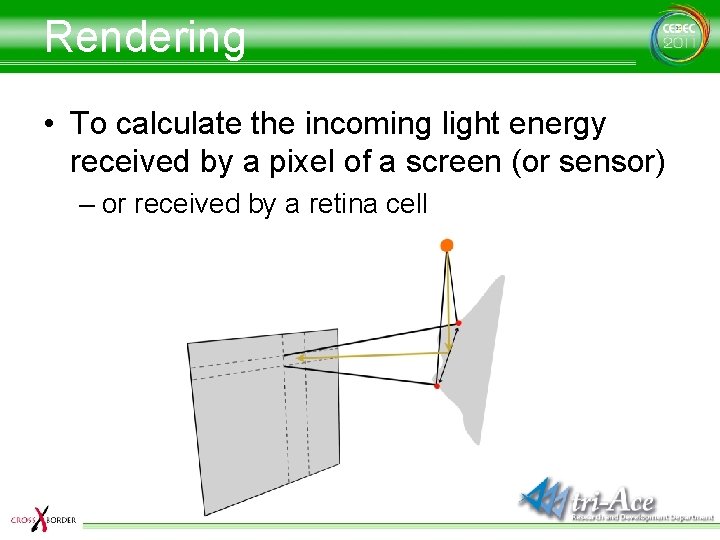
Rendering • To calculate the incoming light energy received by a pixel of a screen (or sensor) – or received by a retina cell
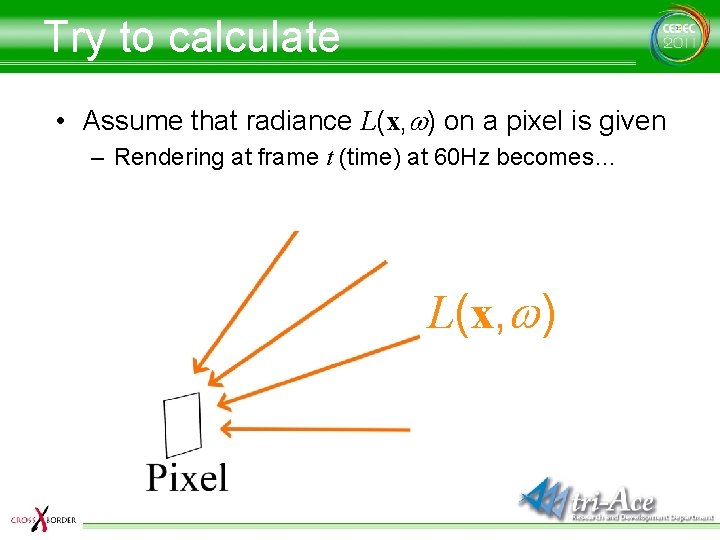
Try to calculate • Assume that radiance L(x, w) on a pixel is given – Rendering at frame t (time) at 60 Hz becomes… L(x, w)

Try to calculate Solution for irradiance from radiance Integrate the incident light (radiance) over the hemisphere Solution for radiant flux from irradiance Integrate the incident light (irradiance) over the pixel domain Solution for radiant energy from radiant flux
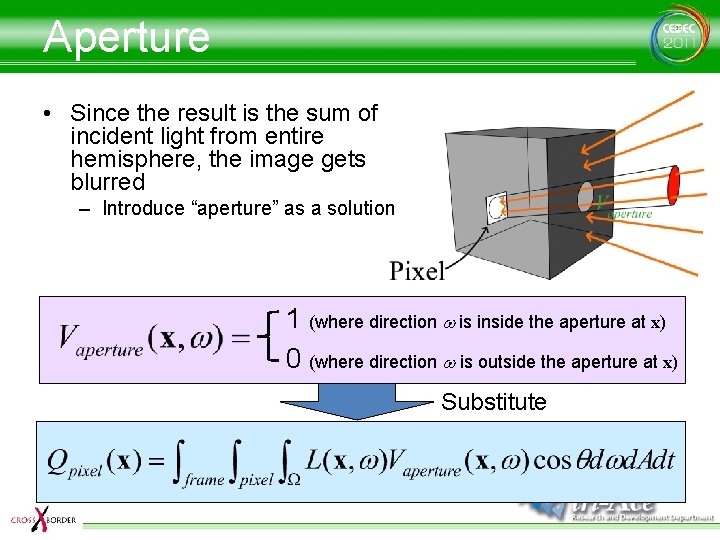
Aperture • Since the result is the sum of incident light from entire hemisphere, the image gets blurred – Introduce “aperture” as a solution 1 (where direction w is inside the aperture at x) 0 (where direction w is outside the aperture at x) Substitute

Without considering the aperture • Generally, real-time rendering doesn’t take into account the aperture is a Dirac’s delta function where the value becomes 1 when direction w equals to direction from x to the center of the virtual aperture Effects of aperture… (with the same intensity of light source) • Smaller aperture size for shaper image (but the image gets darker) • Larger aperture size for brighter image (but the image gets blurrier)
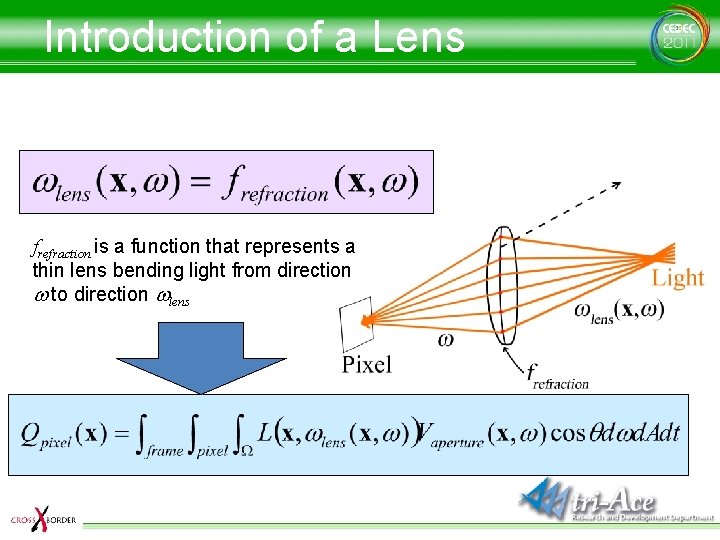
Introduction of a Lens frefraction is a function that represents a thin lens bending light from direction w to direction wlens
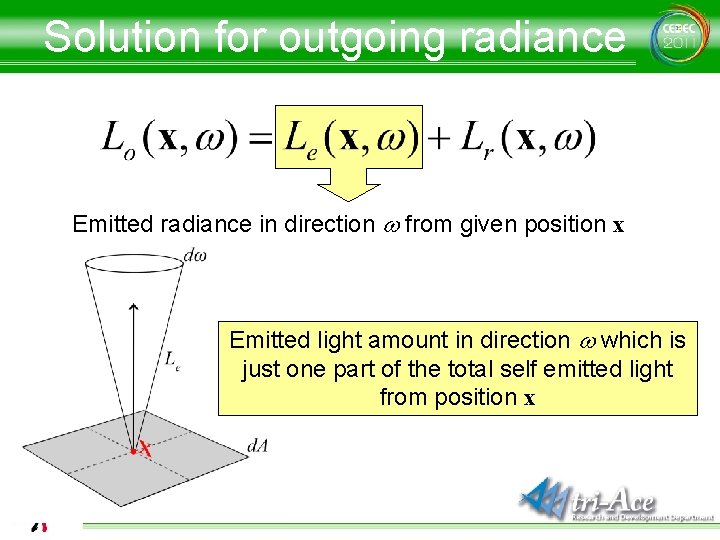
Solution for outgoing radiance Emitted radiance in direction w from given position x Emitted light amount in direction w which is just one part of the total self emitted light from position x

Solution for outgoing radiance Reflected radiance in direction w from given position x Reflected light amount in direction w from the total incident light amount at position x

Then… Outgoing light (radiance) in direction w at given position x = Light amount in direction w for a total light amount of self emission from position x + Reflected light amount in direction w for a total incident light amount at position x

Calculate Le (Self emission) • As you like – Use an arbitrary function • Texture? • Animation curve? • Illumination model? – It represents a light source

Solution for Lr(reflection) • The sum of reflected light for direction w from incident light at position x – Incident light? – Behavior of reflection?

Lr=… Integrate the formula over hemisphere around the normal w’
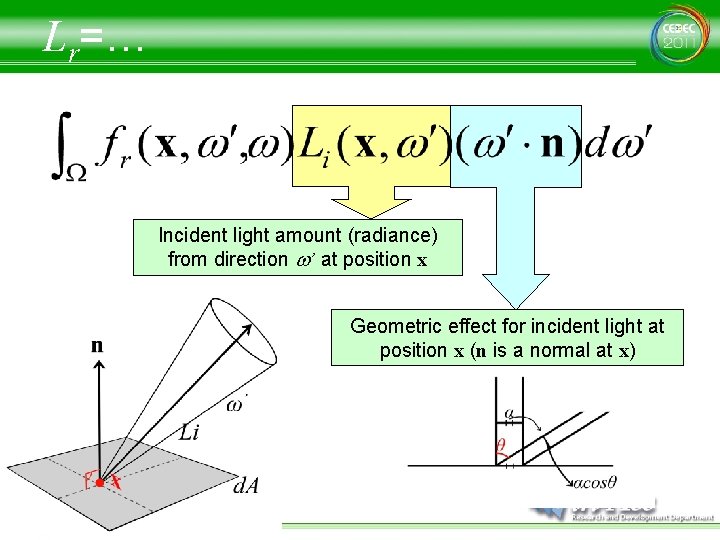
Lr=… Incident light amount (radiance) from direction w’ at position x Geometric effect for incident light at position x (n is a normal at x)

Lr=… A function that represents the ratio between the amount of reflected light for direction w and the amount of incident light from direction w’ at position x = Bi-directional Reflectance Distribution Function (BRDF)

Derive BRDF(1) Differentiate both side by w’ Transpose
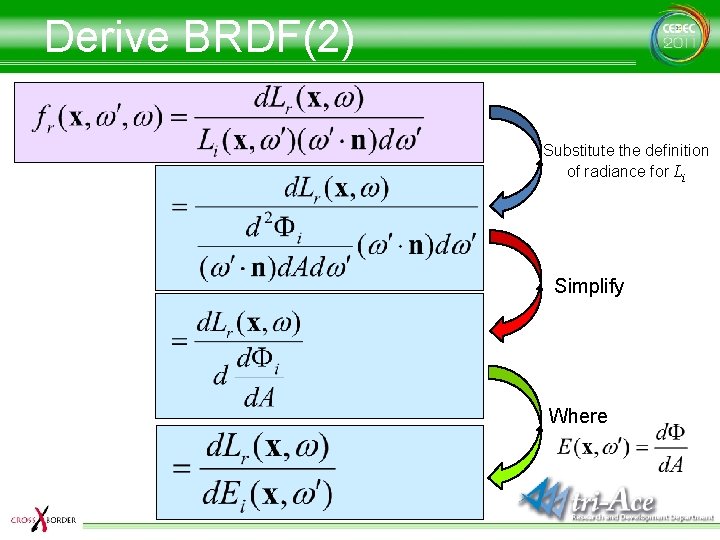
Derive BRDF(2) Substitute the definition of radiance for Li Simplify Where
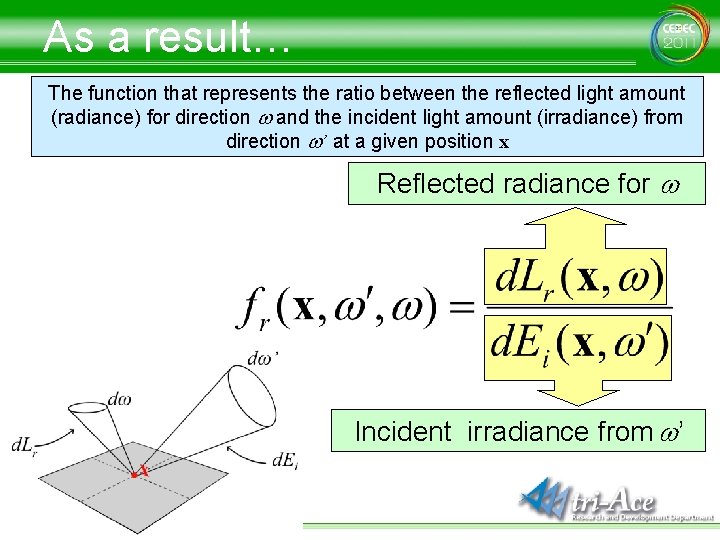
As a result… The function that represents the ratio between the reflected light amount (radiance) for direction w and the incident light amount (irradiance) from direction w’ at a given position x Reflected radiance for w Incident irradiance from w’

Utilize BRDF When light comes • at a given position x – (at a given wavelength l) • from a given direction w’ Reflected light amount can be obtained • for a given direction w

Physical property of BRDF (1) For all w’ The law of conservation of energy The sum of reflected light must not exceed the amount of incoming light "Practical Implementation of physically based shading models at tri-Ace" SIGGRAPH 2010

Physical property of BRDF (2) Helmholtz reciprocity The reflectance stays same when incident direction and reflected direction are swapped
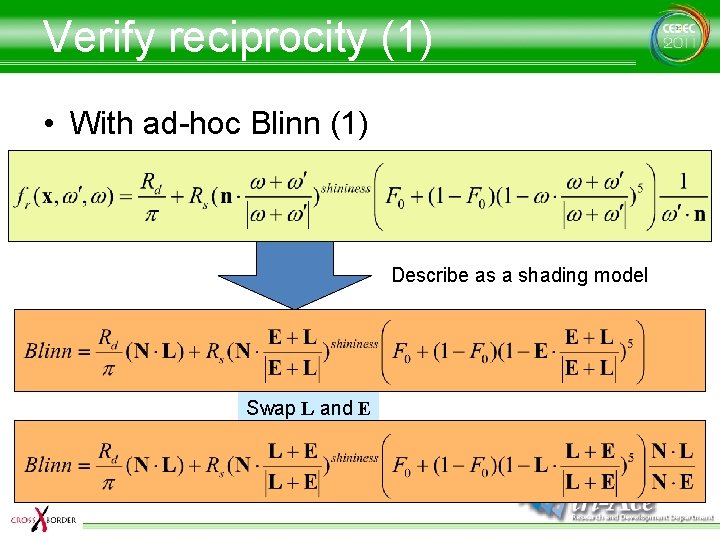
Verify reciprocity (1) • With ad-hoc Blinn (1) Describe as a shading model Swap L and E
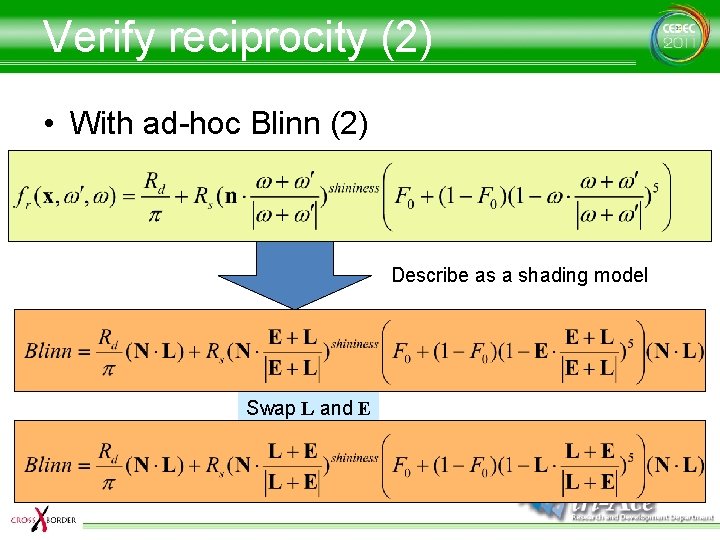
Verify reciprocity (2) • With ad-hoc Blinn (2) Describe as a shading model Swap L and E

Solve the rendering equation Since radiance value is recursively included on both side, to find an analytic solution, it is necessary to look for a solution to the infinite series. Algorithms to find an approximated solution Path tracing, MLT and so on…

Solve it with Lambert(Assumptions) • BRDF (Lambert) x : Shading position xp : Sensor pixel position xa : Aperture position nx : Surface normal at x np : Sensor normal at xp Ap: Area of sensor pixel Ax: Shading area at x Aa: Area of apperture La: Distance from sensor to aperture(focal length) (eye vector) (light vector)
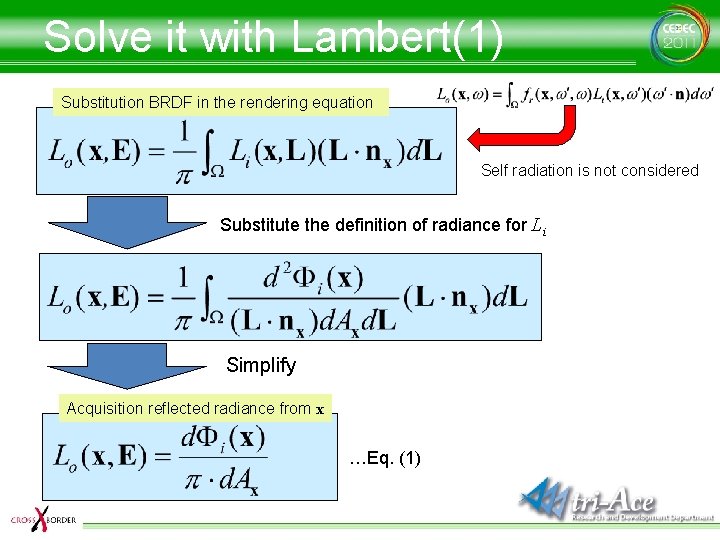
Solve it with Lambert(1) Substitution BRDF in the rendering equation Self radiation is not considered Substitute the definition of radiance for Li Simplify Acquisition reflected radiance from x …Eq. (1)
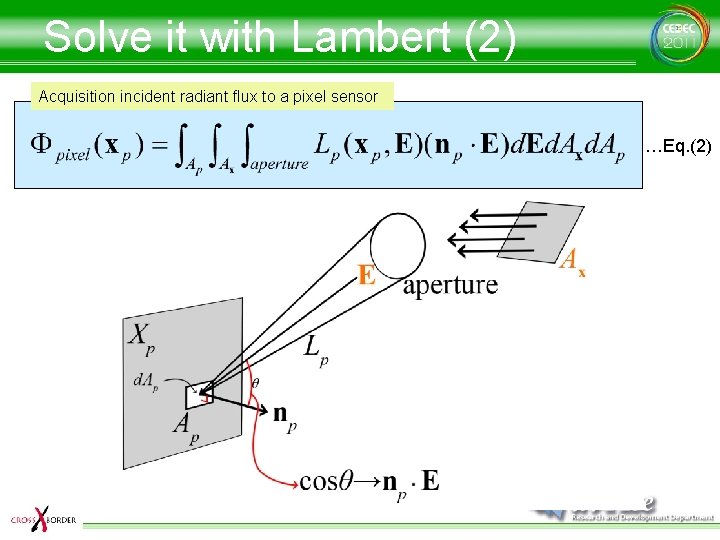
Solve it with Lambert (2) Acquisition incident radiant flux to a pixel sensor …Eq. (2)
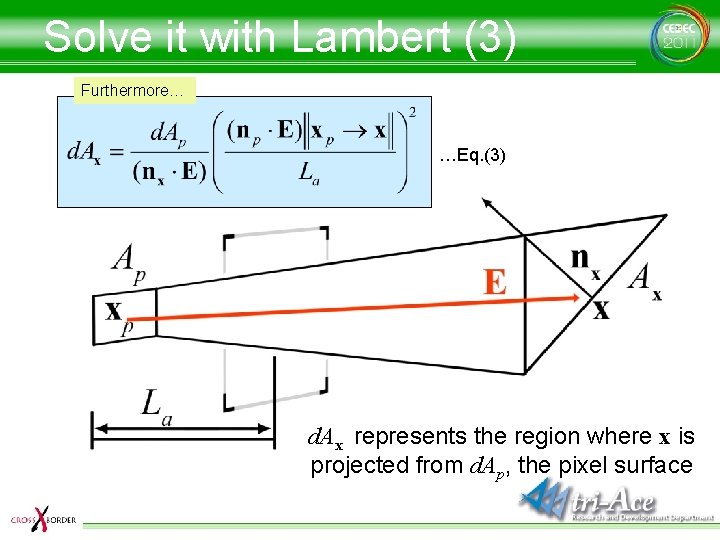
Solve it with Lambert (3) Furthermore… …Eq. (3) d. Ax represents the region where x is projected from d. Ap, the pixel surface
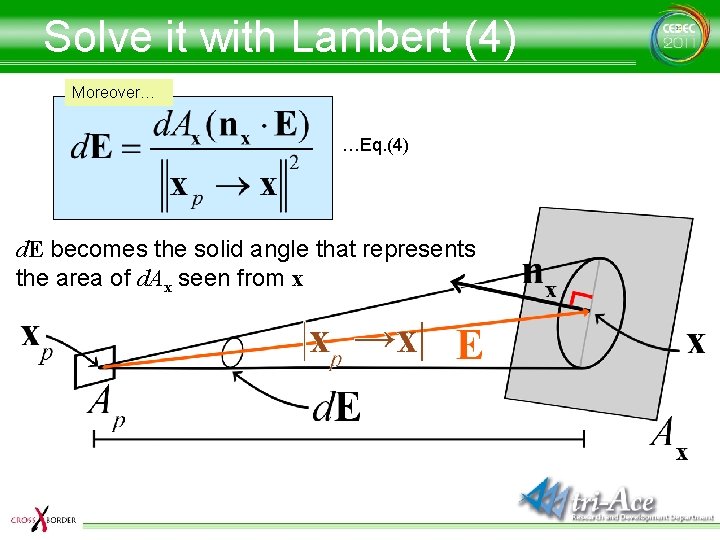
Solve it with Lambert (4) Moreover… …Eq. (4) d. E becomes the solid angle that represents the area of d. Ax seen from x
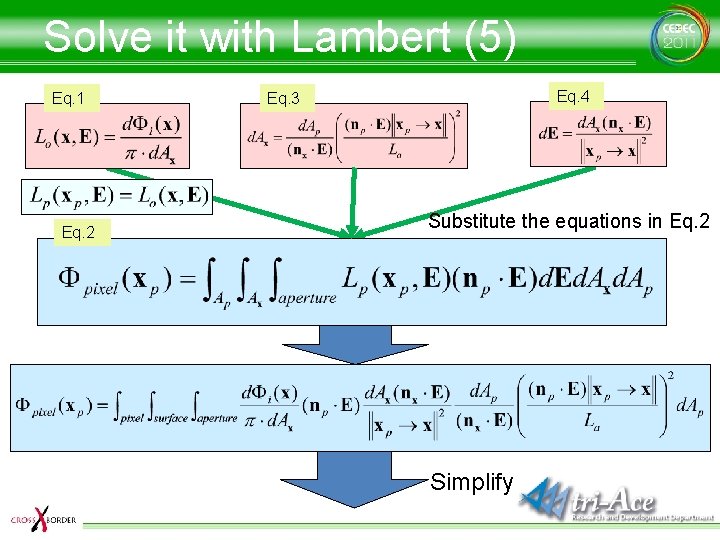
Solve it with Lambert (5) Eq. 1 Eq. 2 Eq. 4 Eq. 3 Substitute the equations in Eq. 2 Simplify
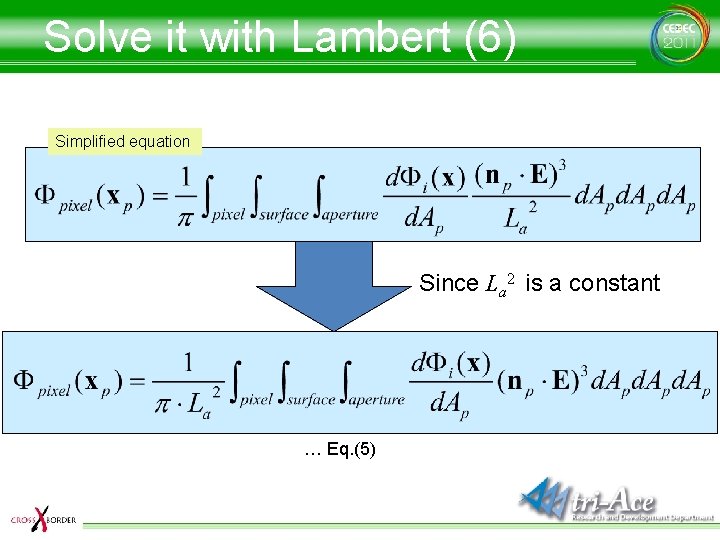
Solve it with Lambert (6) Simplified equation Since La 2 is a constant … Eq. (5)
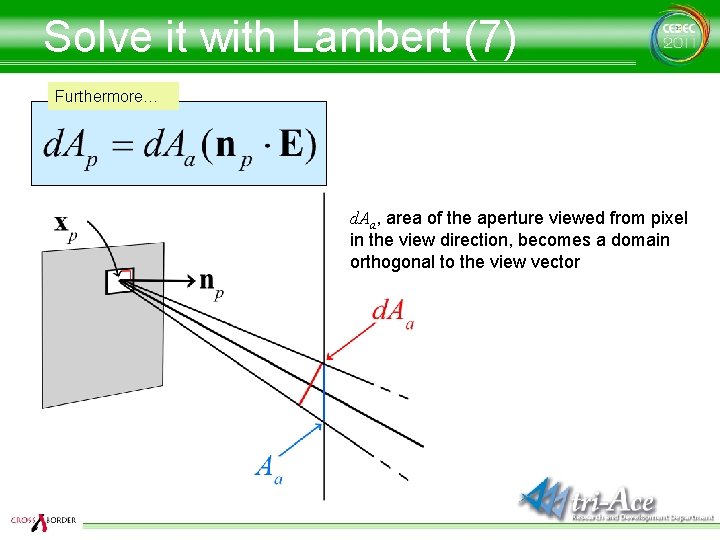
Solve it with Lambert (7) Furthermore… d. Aa, area of the aperture viewed from pixel in the view direction, becomes a domain orthogonal to the view vector
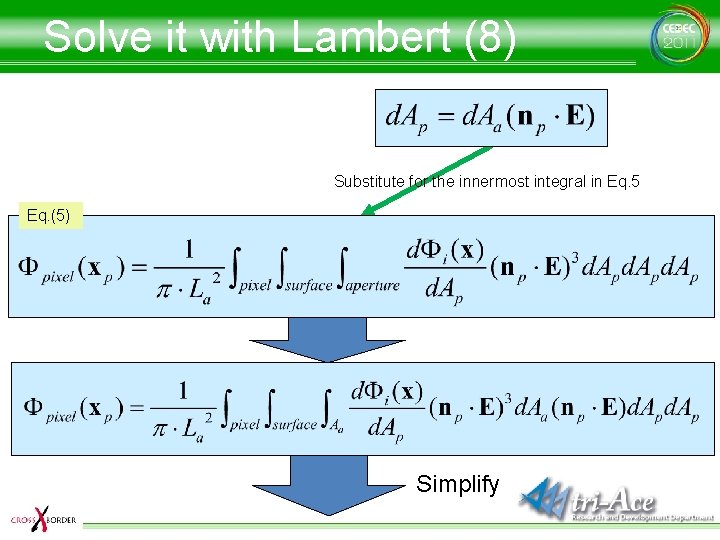
Solve it with Lambert (8) Substitute for the innermost integral in Eq. 5 Eq. (5) Simplify

Solve it with Lambert (9) Simplified equation Simplify more

Solve it with Lambert (10) Final result What does this equation mean?
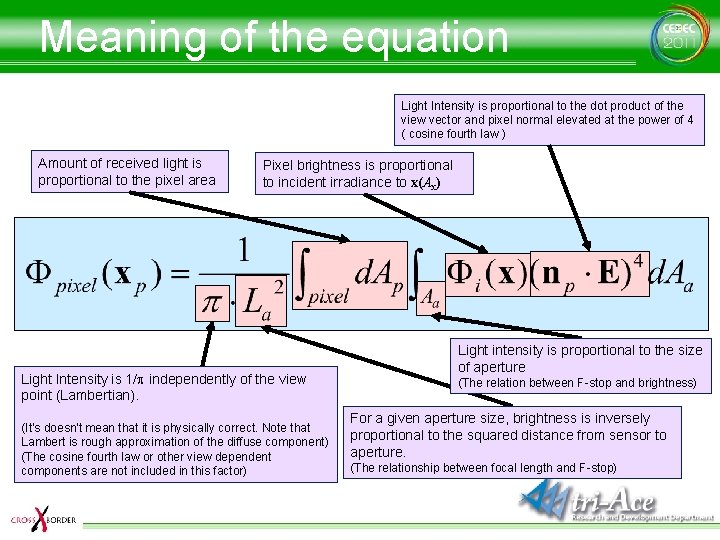
Meaning of the equation Light Intensity is proportional to the dot product of the view vector and pixel normal elevated at the power of 4 ( cosine fourth law ) Amount of received light is proportional to the pixel area Pixel brightness is proportional to incident irradiance to x(Ax) Light Intensity is 1/p independently of the view point (Lambertian). (It's doesn't mean that it is physically correct. Note that Lambert is rough approximation of the diffuse component) (The cosine fourth law or other view dependent components are not included in this factor) Light intensity is proportional to the size of aperture (The relation between F-stop and brightness) For a given aperture size, brightness is inversely proportional to the squared distance from sensor to aperture. (The relationship between focal length and F-stop)

Solve with shader • Real-time ray-traced base algorithms are not realistic on current hardware – Partially available • • • Only diffuse component Point-Based Global Illumination Screen-Space Photon Mapping Precomputed Radiance Transfer and derived ones And so on… • How to solve the equation using shader based on rasterization rendering?

Radiance in shader • How to deal with incident radiance in shader? – A function that represents incident radiance values from hemisphere – Texture? • What is a radiance texture?

Radiance Texture • A texture that stores radiance in each texel Because x (position) is 3 dimensions, w (orientation) is 2, if the equation is used as it is, a 5 dimensional texture is necessary If a light source is assumed to exist in infinite distance…?
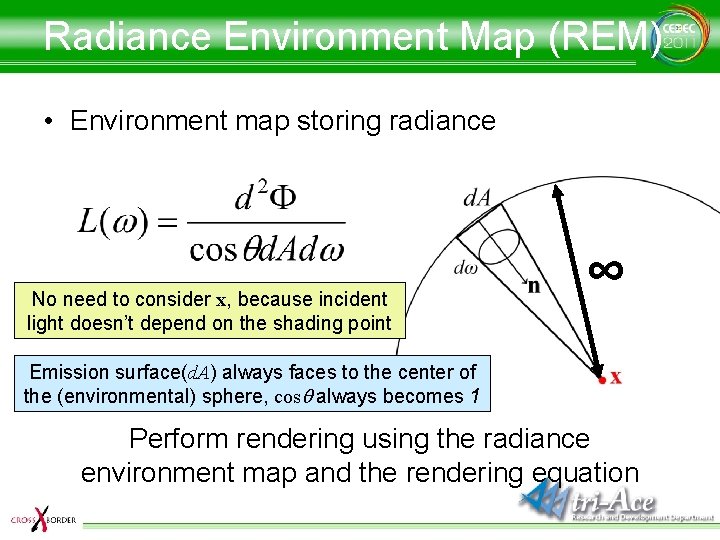
Radiance Environment Map (REM) • Environment map storing radiance No need to consider x, because incident light doesn’t depend on the shading point ∞ Emission surface(d. A) always faces to the center of the (environmental) sphere, cosq always becomes 1 Perform rendering using the radiance environment map and the rendering equation

Generate REM (1) • Generate REM as a cubemap – Ideally, REM would be rendered to a spherical render target – However for ease of implementation, render to a cubemap and compensate for the difference • Conventional real-time rasterization rendering doesn’t store radiant energy or radiant flux in the render target – Directly store radiance computed at the shading pixel in the render target
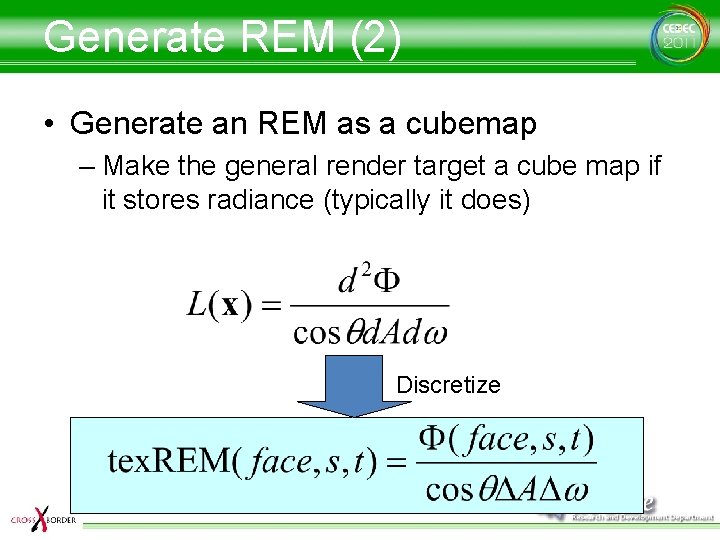
Generate REM (2) • Generate an REM as a cubemap – Make the general render target a cube map if it stores radiance (typically it does) Discretize
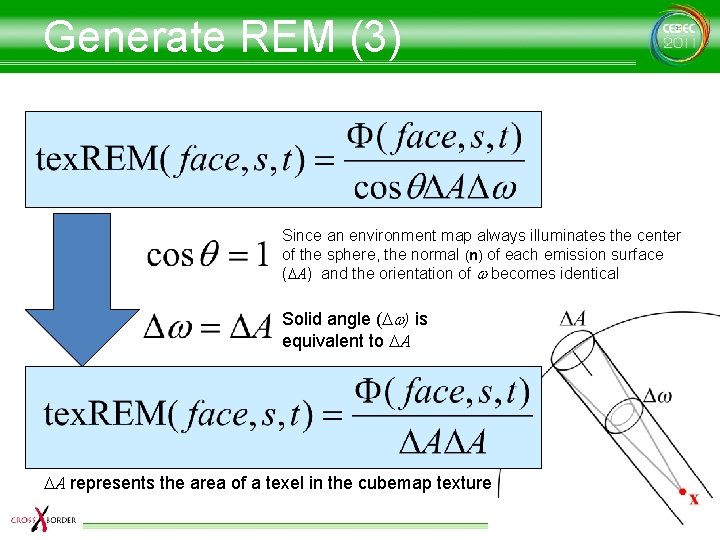
Generate REM (3) Since an environment map always illuminates the center of the sphere, the normal (n) of each emission surface (DA) and the orientation of w becomes identical Solid angle (Dw) is equivalent to DA DA represents the area of a texel in the cubemap texture

Calculate DA • Incident light in the rendering equation is transported from the hemisphere centered around the shading point (x) – Each texel in the cubemap corresponds to a texel over the (hemi-)sphere – DA is equivalent to the area of the spherical quadrilateral that is the cubemap texel projected onto the sphere

Rendering w/REM(assumptions) • Following assumptions are used • Incident light • BRDF (Lambert) • w’ is calculated by projecting the coordinate ( face, s, t) of the cubemap onto the sphere surface • No self-emission

Rendering using REM(1) Substitute in the rendering equation Nothing

Rendering using REM(2) Discretize Substitute the definition of tex. REM
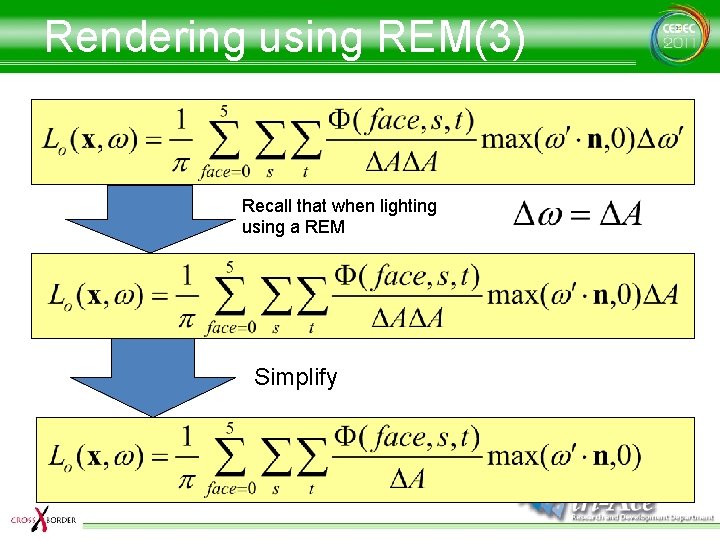
Rendering using REM(3) Recall that when lighting using a REM Simplify

Rendering using REM(4) • Using this radiance, – (ideal) Compute incident radiant flux for each pixel with the rendering equation – (typical) Store it directly in each pixel and use it similar to conventional rendering

Irradiance Environment Map Does this equation calculate irradiance? …similar?

Generate IEM The rendering equation of a Lambertian diffuse surface for one iteration can be calculated using an Irradiance Environment Map and multiplying by 1/p

Optimization • Solving the rendering equation is expensive – Need to solve high dimensional differential equation • Lots of loops • Image resolution is high • Giga or Tera order of computation – Need to drastically reduce computation for real-time rendering • Very rough approximation – A little sacrifice of physically correctness (not physically perfect) – Physically plausible rather than physically perfection

Integral decomposition • Can this integral decompose like this? ≠

Optimize integral • Use Fourier transform (Convolution Theorem) – For convolution (integral of product of two functions), – Apply Fourier transform to each function – Fourier transform of convolution becomes a product of Fourier transformed functions

Convolution theorem • Advantage of convolution theorem – Drastic optimization using Fast Fourier Transform (FFT) • Spherical Harmonics can be regarded as spherical Fourier transform • Spherical Harmonics are easy to use for rendering • FFT and IFFT could have bottleneck in some cases • However, solving the rendering equation in real-time is still too expensive on current generation hardware

Basis transformation • Use basis transformation – More optimization using orthogonal transformation – Reduce unnecessary coefficients for more optimization • Still low frequency? • Using PCA-related algorithms? • Eventually, is it PRT? “Introduction of PRT for game programmers” [CEDEC ‘ 06]

More aggresively • After all, – Does this really not work? – Evaluate what case this approximation works?

Verification (1) ? Verify the problem with discretization ? Verify

Verification (2) Suppose each function… Evaluate this

Verification (3) First term Second term =?
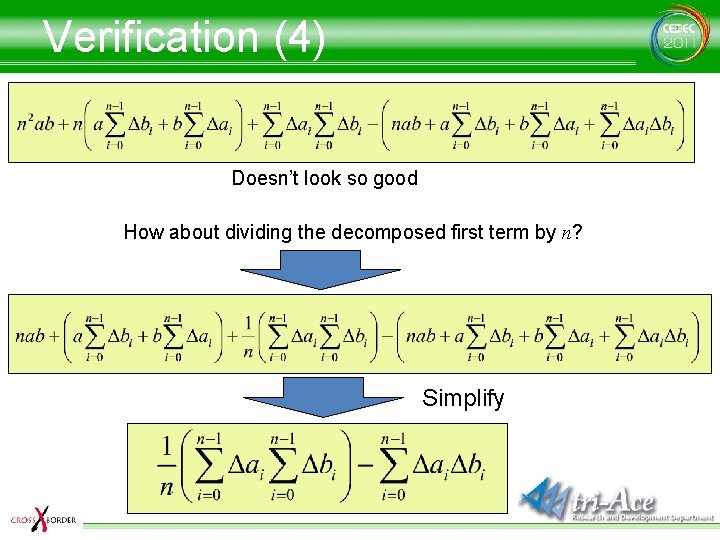
Verification (4) Doesn’t look so good How about dividing the decomposed first term by n? Simplify

Conclusion Since this formula introduces errors, the decomposition becomes a good approximation as the error is close to zero • Good approximation if dealing well with errors – Understand the introduced errors – Visually compare the approximated result to the ground truth (a. k. a. real world)

Wrap up • It is naturally possible to achieve physically correct rendering by using the rendering equation – Because the integration is computed in the code, • It is fair enough to correctly write down the required conditions in mathematical form – Neccesary calculations are not difficult • Drastic optimization according to requirements by hardware specification – Compromised and rough approximation for some cases

Acknowledgements • R&D department, tri-Ace, Inc. – Tatsuya Shoji – Satoshi Ishii – Takafumi Ohshima – Elliott Davis • Thanks for the English version – Sébastien Lagarde, Marc Heng and Naty Hoffman

Questions? http: //research. tri-ace. com
- Slides: 73