Physical Science Chapter 12 Work Machines Section 1

Physical Science Chapter 12 Work & Machines

Section 1: What is Work? § Work is force exerted on an object that causes the object to move some distance § Force without moving a distance yields NO WORK!! Work = Force x Distance; W= Fd SI Unit for work is the Joule 1 Joule = 1 Newton x 1 Meter

Work Makes Something Move § However, in science the word work is used in a different way. § Remember that a force is a push or a pull. In order for work to be done, a force must make something move. § Work is the transfer of energy that occurs when a force makes an object move.

Doing work § If you push against the desk and nothing moves, then you haven't done any work. § There are two conditions that have to be satisfied for work to be done on an object. § One is that the applied force must make the object move, and the other is that the movement must be in the same direction as the applied force.

Doing work § For example, when you lift a stack of books, your arms apply a force upward and the books move upward. Because the force and distance are in the same direction, your arms have done work on the books.

Force and Direction of Motion § The force exerted by your arms on the books is upward, but the books are moving horizontally. § The force you exert is at right angles to the direction the books are moving. § The force exerted by your arms does no work on the books.

Force and Direction of Motion § When you carry books while walking, you might think that your arms are doing work. § However, in this case, the force exerted by your arms does no work on the books.

Work and Energy § When work is done, a transfer of energy always occurs. § This is easy to understand when you think about how you feel after carrying a heavy box up a flight of stairs. § You transferred energy from your moving muscles to the box and increased its potential energy by increasing its height.

Work § transfer of energy through motion § force exerted through a distance W=Fd W: F: d: work (J) force (N) distance (m) 1 J = 1 N·m Distance must be in direction of force!

Power § Power is the amount of work done in one second. It is a rate—the rate at which work is done

Calculating Power § To calculate power, divide the work done by the time that is required to do the work. § The SI unit for power is the watt (W). One watt equals one joule of work done in one second.

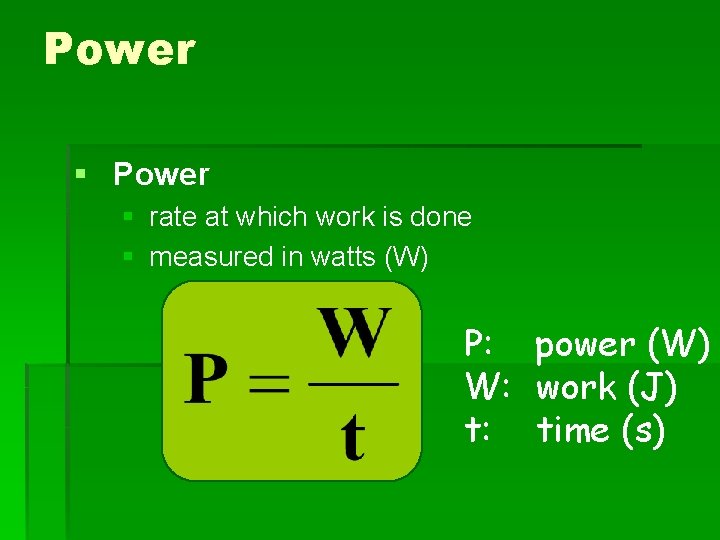
Power § rate at which work is done § measured in watts (W) P: power (W) W: work (J) t: time (s)

Work u Sarah exerts a force of 40 N to pick up her child a distance of 2. 8 m. How much work is done on her child? WORK: GIVEN: W=? F = 40 N D = 2. 8 m F W d W = F·d W = (40 N) · (2. 8 m) W = 112 J

Work u Matt uses a force of 1525 N to drive his car a distance of 381 m. How much work is done on his car? WORK: GIVEN: W=? F = 1525 N D = 381 m F W d W = F·d W = (1525) · (381 m) W = 581025 J

Work GIVEN: u Mark uses 27 J of work to carry the laundry basket with a force of 17 N. What is the distance he carried the laundry basket? W = 27 J F = 17 N d=? F WORK: W d d=W/F d = (27 J) ÷ (17 N) d = 1. 59 m

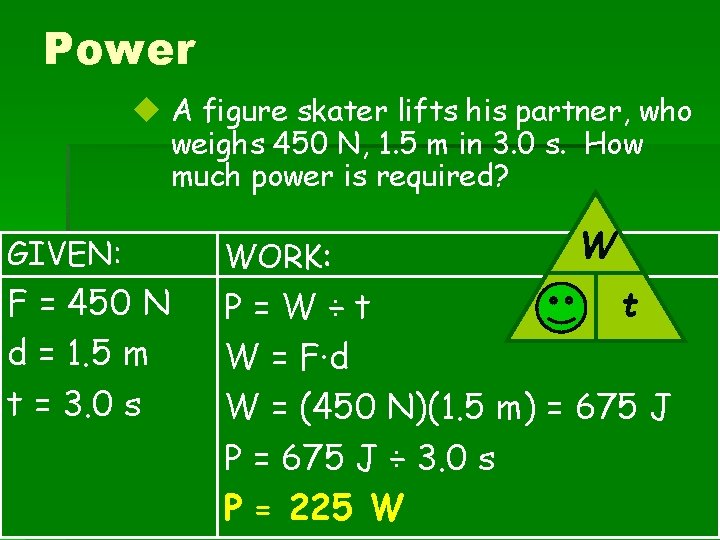
Power u A figure skater lifts his partner, who weighs 450 N, 1. 5 m in 3. 0 s. How much power is required? GIVEN: F = 450 N d = 1. 5 m t = 3. 0 s WORK: W P t P=W÷t W = F·d W = (450 N)(1. 5 m) = 675 J P = 675 J ÷ 3. 0 s P = 225 W

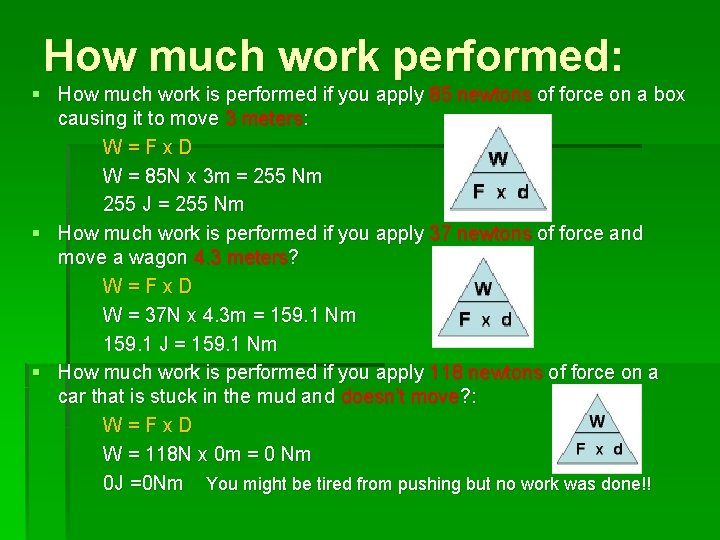
How much work performed: § How much work is performed if you apply 85 newtons of force on a box causing it to move 3 meters: W=Fx. D W = 85 N x 3 m = 255 Nm 255 J = 255 Nm § How much work is performed if you apply 37 newtons of force and move a wagon 4. 3 meters? W=Fx. D W = 37 N x 4. 3 m = 159. 1 Nm 159. 1 J = 159. 1 Nm § How much work is performed if you apply 118 newtons of force on a car that is stuck in the mud and doesn’t move? : W=Fx. D W = 118 N x 0 m = 0 Nm 0 J =0 Nm You might be tired from pushing but no work was done!!

How much force required: § How much force was required to move an object 3 meters if 75 Joules of work were expended? § Formula: Work = Force x Distance § Need to solve for Force, w= 75 J & D=3 M 75 J = F x 3 M 75 NM / 3 M = F 25 N = F

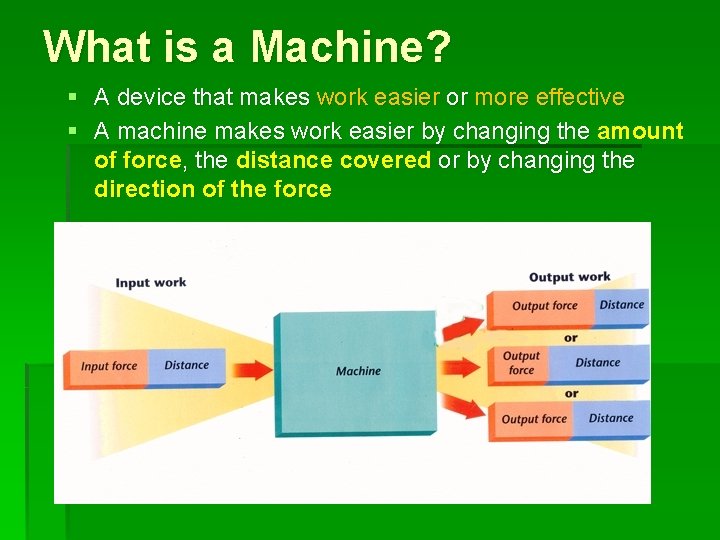
What is a Machine? § A device that makes work easier or more effective § A machine makes work easier by changing the amount of force, the distance covered or by changing the direction of the force

Section 2 Mechanical Advantage § A machine’s mechanical advantage is the number of times a force exerted on a machine is multiplied. § Ideal Mechanical Advantage has no units ( they cancel each other out when doing the math problem § IMA = output force / input force or IMA = resistance force / effort force

Section 2 Efficiency of a Machine § The amount of work obtained from a machine is always less than the amount of work put into it. This is because work is lost to friction. § Efficiency = output work / input work x 100 Remember that work = force x distance

Section 3 Simple Machines

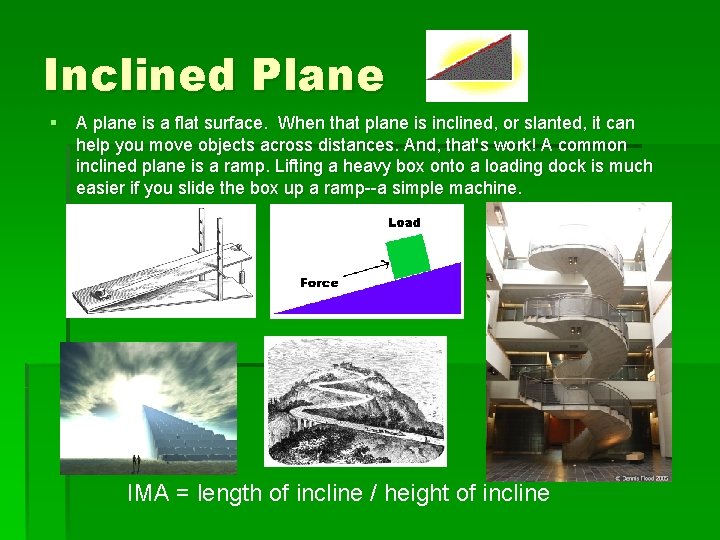
Inclined Plane § A plane is a flat surface. When that plane is inclined, or slanted, it can help you move objects across distances. And, that's work! A common inclined plane is a ramp. Lifting a heavy box onto a loading dock is much easier if you slide the box up a ramp--a simple machine. IMA = length of incline / height of incline

Wedge § you can use the edge of an inclined plane to push things apart. Then, the inclined plane is a wedge. So, a wedge is actually a kind of inclined plane. An axe blade is a wedge. Think of the edge of the blade. It's the edge of a smooth slanted surface.

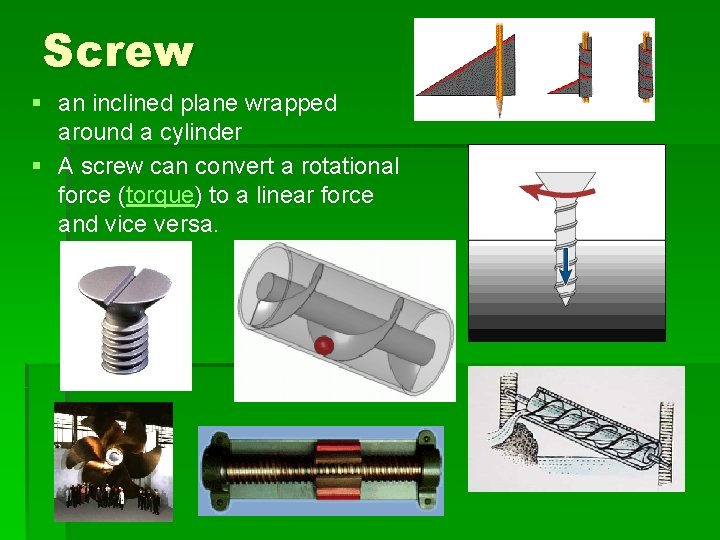
Screw § an inclined plane wrapped around a cylinder § A screw can convert a rotational force (torque) to a linear force and vice versa.

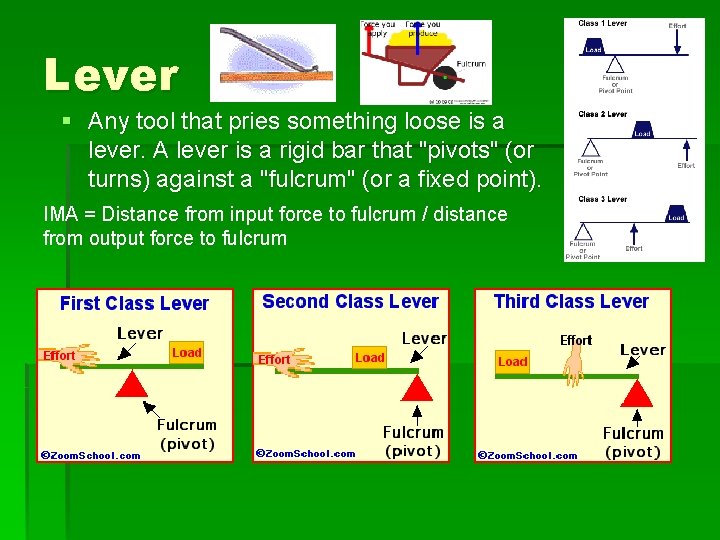
Lever § Any tool that pries something loose is a lever. A lever is a rigid bar that "pivots" (or turns) against a "fulcrum" (or a fixed point). IMA = Distance from input force to fulcrum / distance from output force to fulcrum

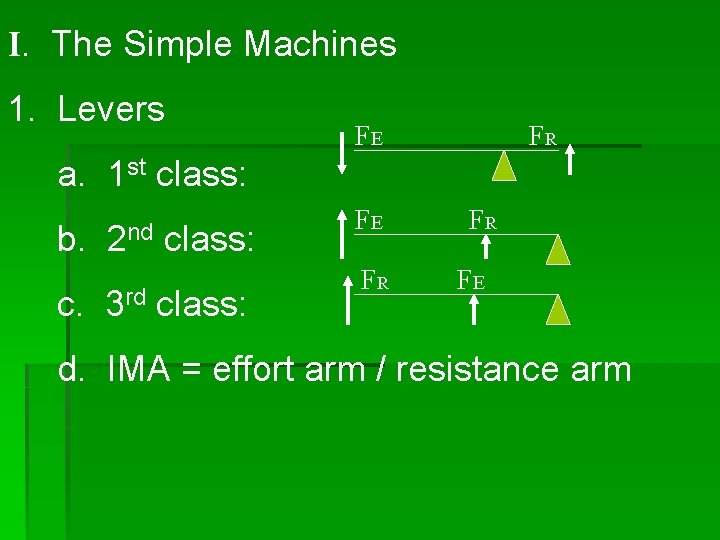
I. The Simple Machines 1. Levers FE FR a. 1 st class: b. 2 nd class: c. 3 rd class: FE FR FR FE d. IMA = effort arm / resistance arm

1 st Class Levers § Notice how § The input & output forces are in opposite directions § The fulcrum is between the input & output forces § Examples include nail remover, paint can opener scissors, seesaw

2 nd Class Levers § Notice how: § The input & output forces are in the same direction § Input force is farther away from the fulcrum than the output force § Examples include: wheel barrow, door, nutcracker

3 rd Class Lever § Notice how: § The input & output forces are in the same direction § The input force is closer to the fulcrum than the output force § Examples include rake, shovel, baseball bat and fishing pole

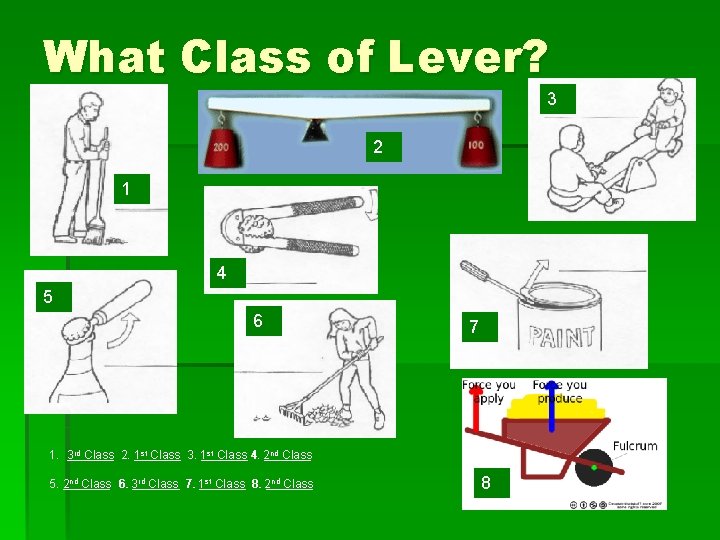
What Class of Lever? 3 2 1 4 5 6 7 st Class 4. 2 nd Class 1. _______ 3 rd Class 2. _______ 1 st Class 3. 1 _______ nd Class 6. rd Class 7. 1 st Class 8. nd Class 5. 2 _______ 6. 3_______ 8. 2_______ 8

Wheel and Axle § two circular objects attached together about a common axis § Wheel is the large cylinder § Axle is the small cylinder IMA = Radius of the wheel / Radius of the axle

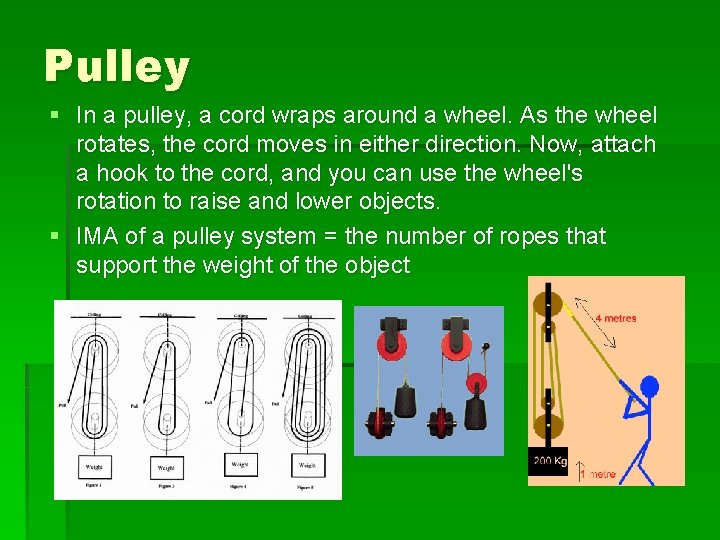
Pulley § In a pulley, a cord wraps around a wheel. As the wheel rotates, the cord moves in either direction. Now, attach a hook to the cord, and you can use the wheel's rotation to raise and lower objects. § IMA of a pulley system = the number of ropes that support the weight of the object

2. Pulleys a. Fixed pulley 1) changes only the direction of a force 2) always has IMA = 1 b. Movable pulley 1) attached to object 2) IMA = 2

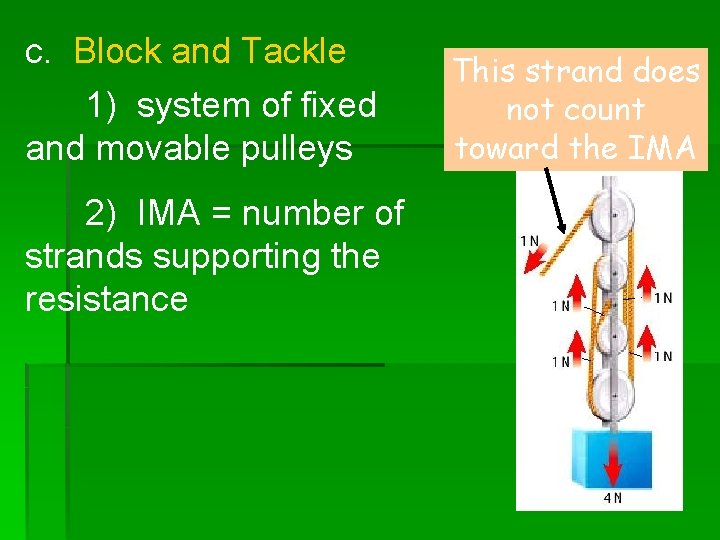
c. Block and Tackle 1) system of fixed and movable pulleys 2) IMA = number of strands supporting the resistance This strand does not count toward the IMA

Word Problems § Word problems can be confusing; but w/ some practice they’re not that bad. Here a few hints to make them easier § 1. Be sure you remember the “Need-to-Know” formulas § S =d/t ; A = Vf – Vi ; F = MA ; W=Fx. D; Power = Work/Time § In the word problem be sure you know the units for each of the variables in the particular formula being discussed. § Distance – Meter; Force – Newton; Volume - cm 3 or Liter § 2. In the word problem, all but one of the variables is told to you in one way or another. Identify what variable is being asked to solve, then plug in the remaining variables to the formula § Solve it!! Make sure you also keep track of the units