Physical Quantities and Measurement What is Physics Natural

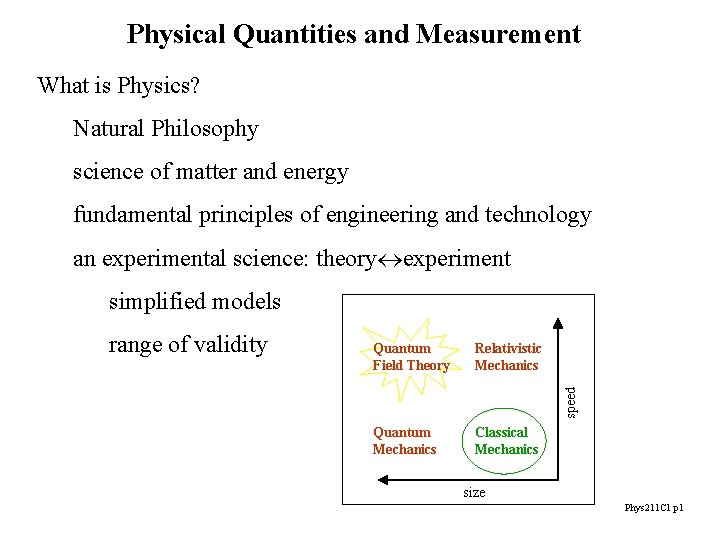
Physical Quantities and Measurement What is Physics? Natural Philosophy science of matter and energy fundamental principles of engineering and technology an experimental science: theory experiment simplified models Quantum Field Theory Relativistic Mechanics Quantum Mechanics Classical Mechanics speed range of validity size Phys 211 C 1 p 1

Quantifying predictions and observations physical quantities: numbers used to describe physical phenomena height, weight e. g. may be defined operationally standard units: International System (SI aka Metric) defined units established in terms of a physical quantity derived units established as algebraic combinations of other units Phys 211 C 1 p 2

Scientific Notation: powers of 10 5, 820 = 5. 82 x 103 = 5. 82 E 3. 000527 = 5. 28 x 10 -4 = 5. 28 E-4 note: 103 = 1 x 103 =1 E 3 not 10 E 3! Common prefixes How big (in terms of everyday life/other things) is a meter nanometer centimeter kilometer gram kilogram Phys 211 C 1 p 3

Dimensional Analysis: consistency of units Algebraic equations must always be dimensionally consistent. You can’t add apples and oranges! converting units treat units as algebraic quantities multiplying or dividing a quantity by 1 does not affect its value Phys 211 C 1 p 4

Some Useful Conversion factors: 1 inch = 2. 54 cm 1 m = 3. 28 ft 1 mile = 5280 ft 1 mile = 1. 61 km Units Conversion Examples Example 1 -1 The world speed record, set in 1983 is 1019. 5 km/hr. Express this speed in m/s Example how man cubic inches are there in a 2 liter engine? Phys 211 C 1 p 5

Significant Figures and Uncertainty Every measurement of a physical quantity involves some error random error averages out small random error accurate measurement systematic error does not average out small systematic error precise measurement less precise less accurate Phys 211 C 1 p 6

Indicating the accuracy of a number: x ± Dx or x± dx nominal value: the indicated result of the measurement numerical uncertainty: how much the “actual value” might be expected to differ from the nominal value sometimes called the numerical error 1 standard deviation A measured length of 20. 3 cm ±. 5 cm means that the actual length is expected to lie between 19. 8 cm and 20. 8 cm. It has a nominal value of x = 20. 3 cm with an uncertainty of Dx. 5 cm. fractional uncertainty: the fraction of the nominal value corresponding to the numerical uncertainty percentage uncertainty: the percentage of the nominal value corresponding to the numerical uncertainty Phys 211 C 1 p 7

Uncertainties in calculations Adding and subtracting: add numerical uncertainty Multiplying or Dividing: add fractional/percentage uncertainty Powers are “multiple multiplications” Phys 211 C 1 p 8

More complex algebraic expressions must be broken down operation by operation a = 3. 13±. 05 b = 7. 14 ±. 01 c = 14. 44 ±. 2% Phys 211 C 1 p 9

Significant Figures: common way of implicitly indicating uncertainty number is only expressed using meaningful digits (sig. figs. ) last digit (the least significant digit = lsd) is uncertain 3 3. 00 one digit two digits (two significant figures = 2 sig. figs. ) three digits, etc. (300 how many digits? ) Combining numbers with significant digits Addition and Subtraction: least significant digit determined by decimal places (result is rounded). 57 +. 3 =. 87 =. 9 11. 2 - 17. 63 = -6. 4 Multiplication and Division: number of significant figures is the number of sig. figs. of the factor with the fewest sig. figs. 1. 3 x 7. 24 = 9. 412 = 9. 4 17. 5/. 3794 = 46. 12546 = 46. 1 Integer factors and geometric factors (such as p) have infinite precision p x 3. 762 = 44. 4145803 = 44. 4 Phys 211 C 1 p 10

Estimates and Order of magnitude calculations an order of magnitude is a (rounded) 1 sig fig calculation, whose answer is expressed as the nearest power of 10. Estimates should be done “in your head” check against calculator mistakes! Additional Homework: with a = 3. 13±. 05 b = 7. 14 ±. 01 c = 14. 44 ±. 2% evaluate expressions (nominal value and uncertainty expressed as numerical uncertainty and percentage uncertainty) Phys 211 C 1 p 11