Physical Limits of Computing Dr Mike Frank Slides

Physical Limits of Computing Dr. Mike Frank Slides from a Course Taught at the University of Florida College of Engineering Department of Computer & Information Science & Engineering Spring 2000, Spring 2002, Fall 2003

Overview of First Lecture • Introduction: Moore’s Law vs. Known Physics • Mechanics of the course: – Course website – Books / readings – Topics & schedule – Assignments & grading policies – misc. other administrivia

Physical Limits of Computing Introductory Lecture Moore’s Law vs. Known Physics

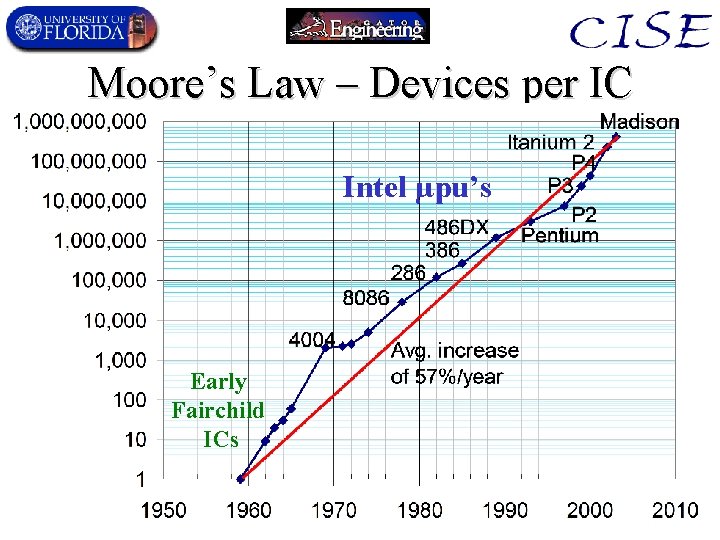
Moore’s Law • Moore’s Law proper: – Trend of doubling of number of transistors per integrated circuit every 18 (later 24) months • First observed by Gordon Moore in 1965 (see readings) • “Generalized Moore’s Law” – Various trends of exponential improvement in many aspects of information processing technology (both computing & communication): • Storage capacity/cost, clock frequency, performance/cost, size/bit, cost/bit, energy/operation, bandwidth/cost …

Moore’s Law – Devices per IC Intel µpu’s Early Fairchild ICs

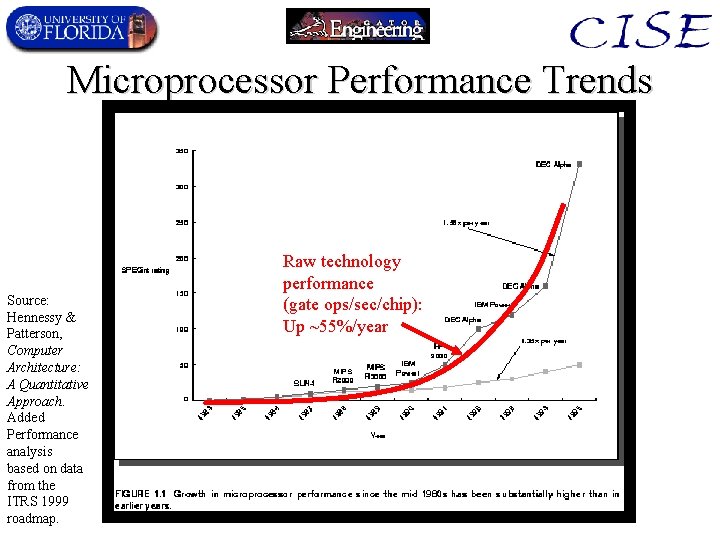
Microprocessor Performance Trends Source: Hennessy & Patterson, Computer Architecture: A Quantitative Approach. Added Performance analysis based on data from the ITRS 1999 roadmap. Raw technology performance (gate ops/sec/chip): Up ~55%/year

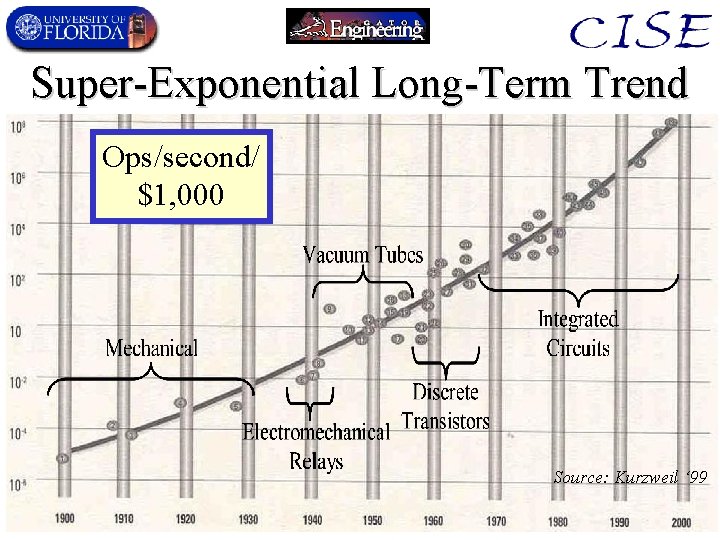
Super-Exponential Long-Term Trend Ops/second/ $1, 000 Source: Kurzweil ‘ 99

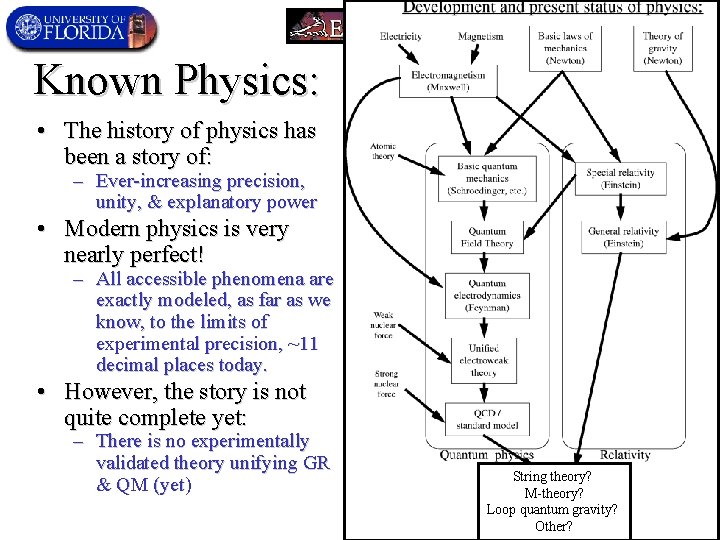
Known Physics: • The history of physics has been a story of: – Ever-increasing precision, unity, & explanatory power • Modern physics is very nearly perfect! – All accessible phenomena are exactly modeled, as far as we know, to the limits of experimental precision, ~11 decimal places today. • However, the story is not quite complete yet: – There is no experimentally validated theory unifying GR & QM (yet) String theory? M-theory? Loop quantum gravity? Other?

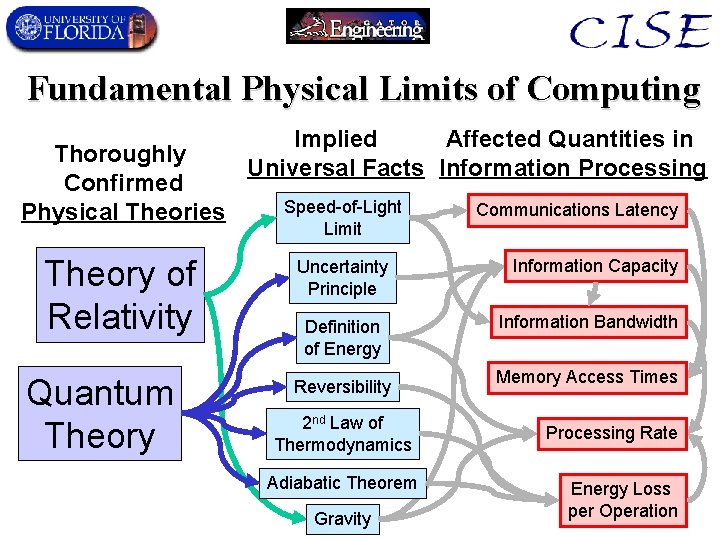
Fundamental Physical Limits of Computing Thoroughly Confirmed Physical Theories Theory of Relativity Quantum Theory Implied Affected Quantities in Universal Facts Information Processing Speed-of-Light Limit Uncertainty Principle Definition of Energy Reversibility 2 nd Law of Thermodynamics Adiabatic Theorem Gravity Communications Latency Information Capacity Information Bandwidth Memory Access Times Processing Rate Energy Loss per Operation

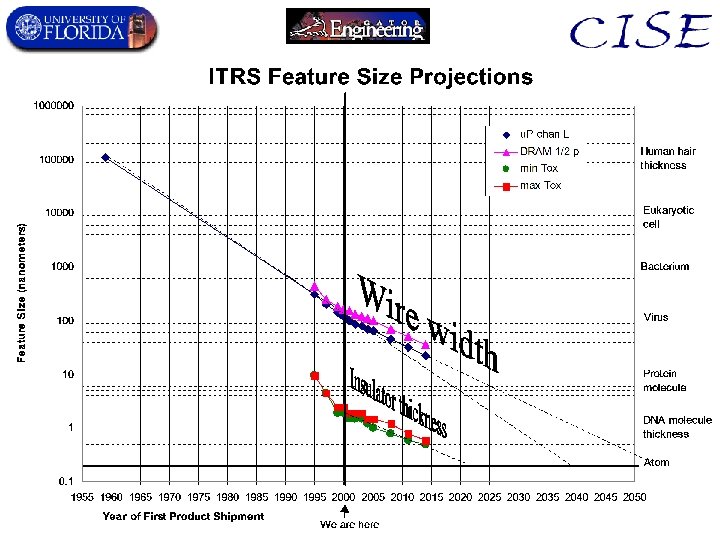
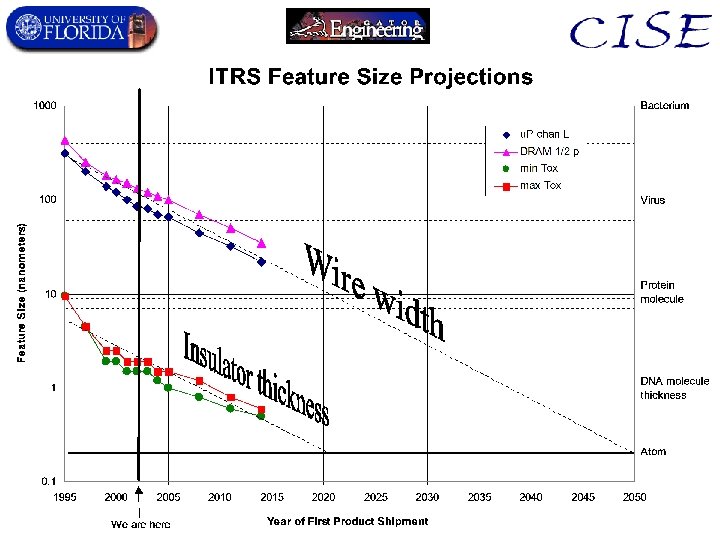
A Precise Definition of Nanoscale 10− 4. 5 m ≈ 31. 6 µm Microscale: Characteristic length scale in Microcomputers 10− 6 m = 1 µm 10− 7. 5 m ≈ 31. 6 nm 10− 9 m = 1 nm ~Atom size 10− 10. 5 m ≈ 31. 6 pm 10− 12 m = 1 pm Near nanoscale Far nanoscale Nanoscale: Characteristic length scale in Nanocomputers Picoscale: Characteristic length scale in Picocomputers (if possible)

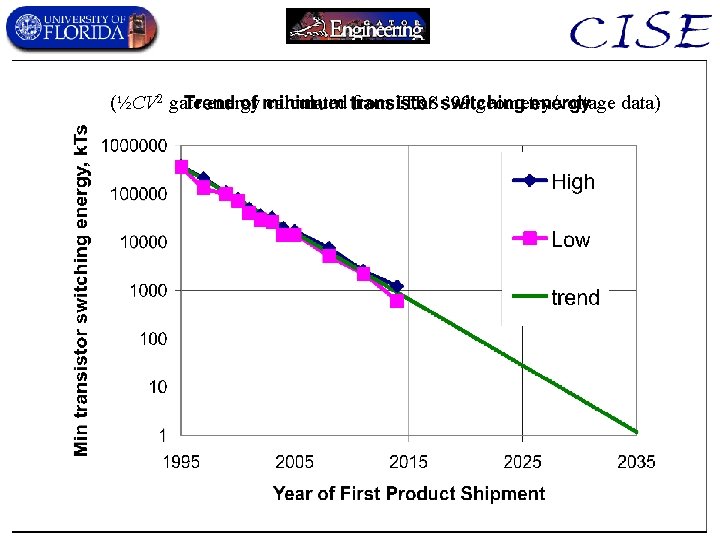
(½CV 2 gate energy calculated from ITRS ’ 99 geometry/voltage data)

What is entropy? • First was characterized by Rudolph Clausius in 1850. – Originally was just defined as heat ÷ temperature. – Noted to never decrease in thermodynamic processes. – Significance and physical meaning were mysterious. • In ~1880’s, Ludwig Boltzmann proposed that entropy S is the logarithm of the number N of states, S = k ln N – What we would now call the information capacity of a system – Holds for systems at equilibrium, in maximum-entropy state • The modern consensus that emerged from 20 th-century physics is that entropy is indeed the amount of unknown or incompressible information in a physical system. – Important contributions to this understanding were made by von Neumann, Shannon, Jaynes, and Zurek.

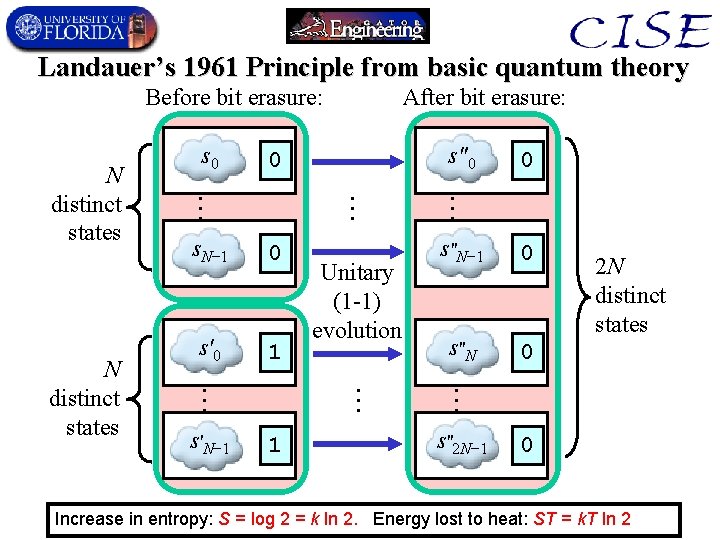
Landauer’s 1961 Principle from basic quantum theory Before bit erasure: 0 s′ 0 1 1 s″N− 1 0 s ″N 0 2 N distinct states … … s′N− 1 Unitary (1 -1) evolution 0 … … s. N− 1 … N distinct states s″ 0 0 … N distinct states s 0 After bit erasure: s″ 2 N− 1 0 Increase in entropy: S = log 2 = k ln 2. Energy lost to heat: ST = k. T ln 2

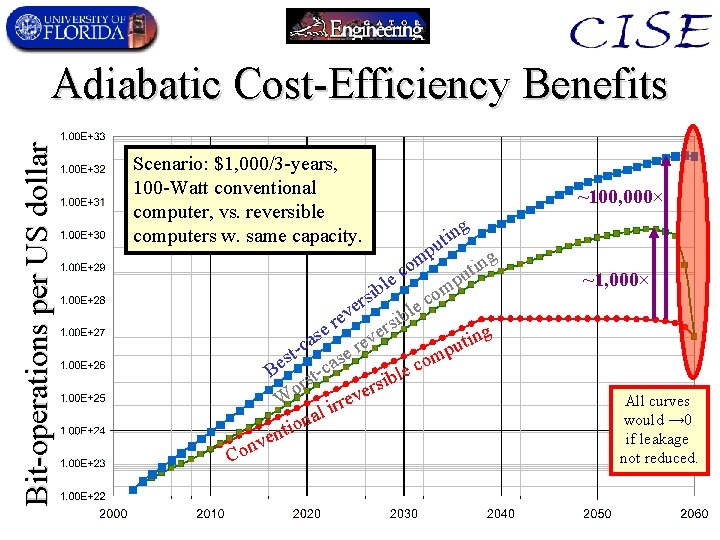
Bit-operations per US dollar Adiabatic Cost-Efficiency Benefits Scenario: $1, 000/3 -years, 100 -Watt conventional computer, vs. reversible computers w. same capacity. ~100, 000× g tin u p Co ng i om t c e pu l m b i s co r e e bl ev i r s g er se n v i a t e pu t-c se r m s co Be st-ca e l sib r or e ev W r r i al n o ti n e nv ~1, 000× All curves would → 0 if leakage not reduced.