PHYS 274 Quantum Mechanics VI Max Born 1882

PHYS 274: Quantum Mechanics VI Max Born, 1882 Quantum Dots – Further basics of Quantum Mechanics 1970 – Particle in a finite box and tunneling – Also review/reread QM harmonic oscillator Today’s theme: Matching of boundary conditions in QM 1

Announcements Next Midterm: Monday November 13 th will cover waves as particles (Chap 38), particles as waves (Chap 39) and quantum mechanics (Chap 40).

The Born Interpretation of Quantum Mechanics In 1926, age 34, Max Born proposed that |ψ|2 is the probability distribution function for a particle that is described by a wavefunction ψ. He also coined the term “Quantenmechanik”. He received the 1954 Nobel Prize in Physics. He fled to the UK in 1933 when the Nazi’s came to power. Olivia Newton John, singer and star of Grease is his grand-daughter https: //www. youtube. com/watch? v=v. Wz 9 VN 40 n. CA 1981 Hit song: “Let’s get physical”
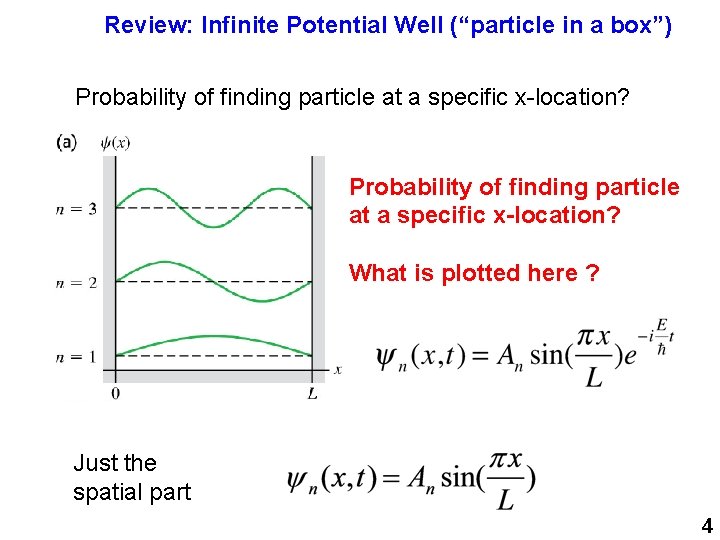
Review: Infinite Potential Well (“particle in a box”) Probability of finding particle at a specific x-location? What is plotted here ? Just the spatial part 4
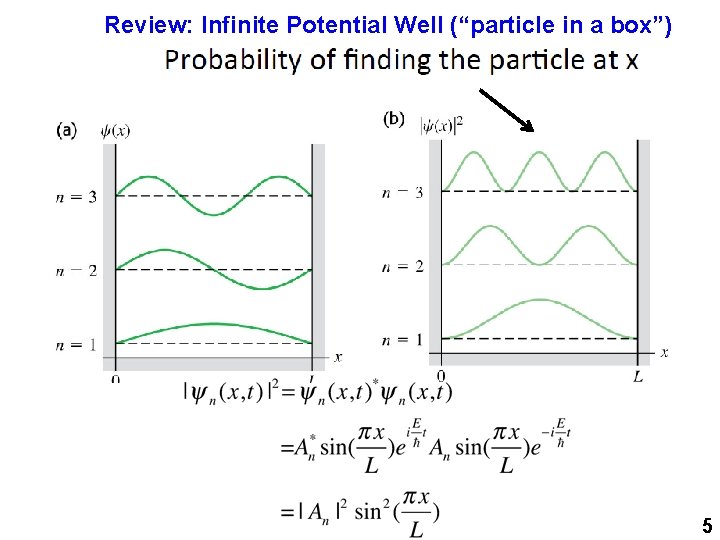
Review: Infinite Potential Well (“particle in a box”) 5
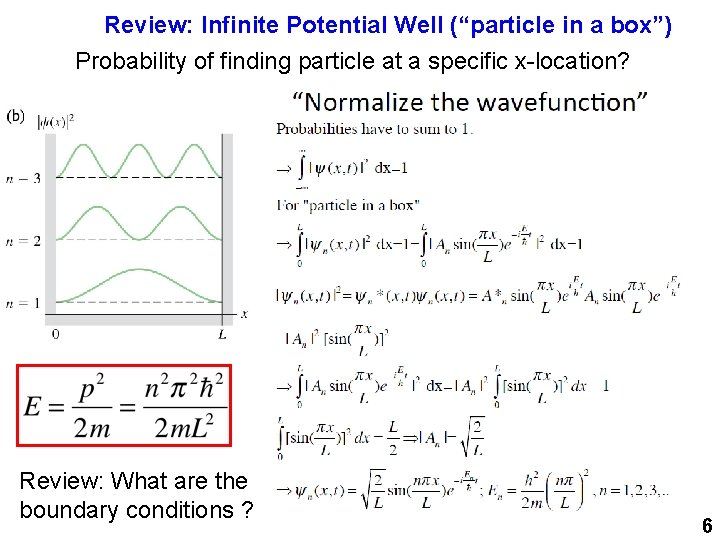
Review: Infinite Potential Well (“particle in a box”) Probability of finding particle at a specific x-location? Review: What are the boundary conditions ? 6
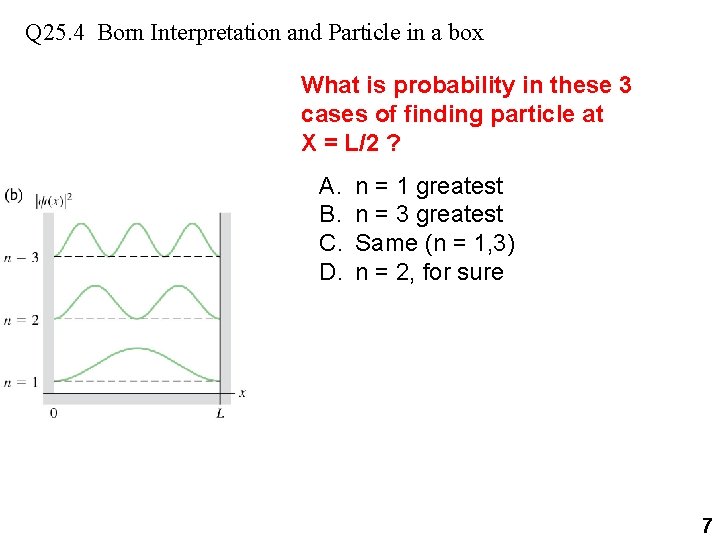
Q 25. 4 Born Interpretation and Particle in a box What is probability in these 3 cases of finding particle at X = L/2 ? A. B. C. D. n = 1 greatest n = 3 greatest Same (n = 1, 3) n = 2, for sure 7
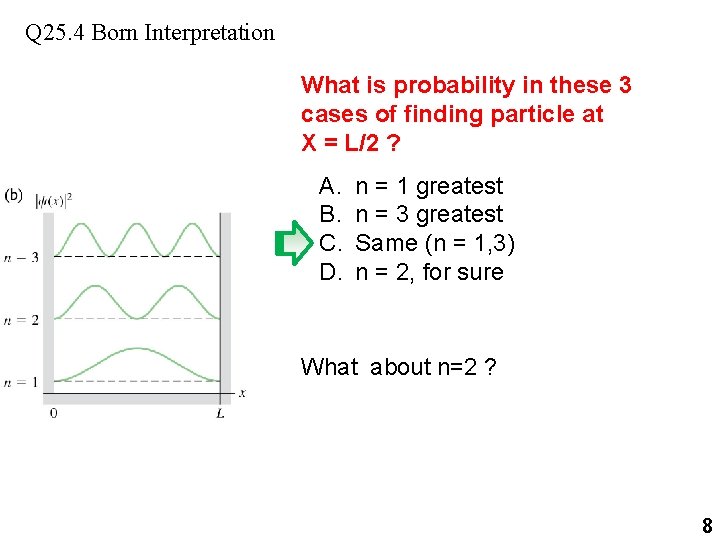
Q 25. 4 Born Interpretation What is probability in these 3 cases of finding particle at X = L/2 ? A. B. C. D. n = 1 greatest n = 3 greatest Same (n = 1, 3) n = 2, for sure What about n=2 ? 8
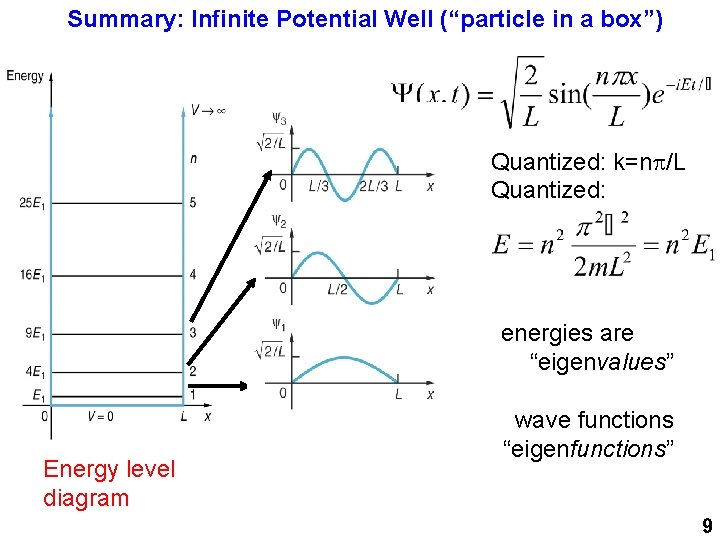
Summary: Infinite Potential Well (“particle in a box”) Quantized: k=np/L Quantized: energies are “eigenvalues” Energy level diagram wave functions “eigenfunctions” 9
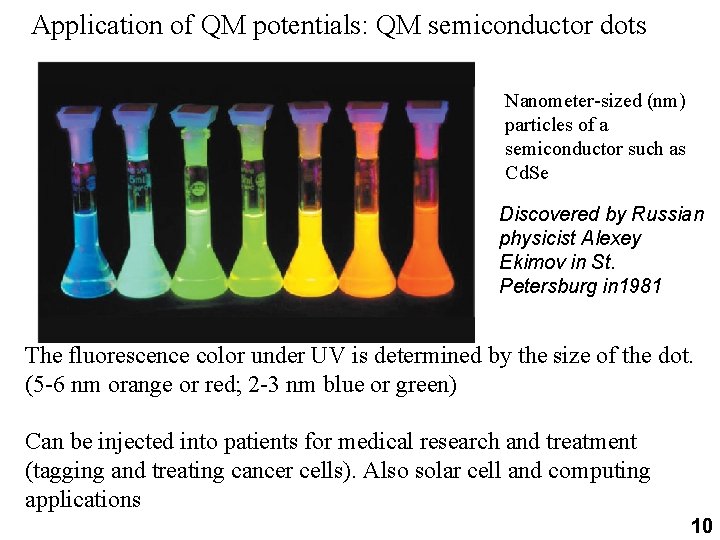
Application of QM potentials: QM semiconductor dots Nanometer-sized (nm) particles of a semiconductor such as Cd. Se Discovered by Russian physicist Alexey Ekimov in St. Petersburg in 1981 The fluorescence color under UV is determined by the size of the dot. (5 -6 nm orange or red; 2 -3 nm blue or green) Can be injected into patients for medical research and treatment (tagging and treating cancer cells). Also solar cell and computing applications 10
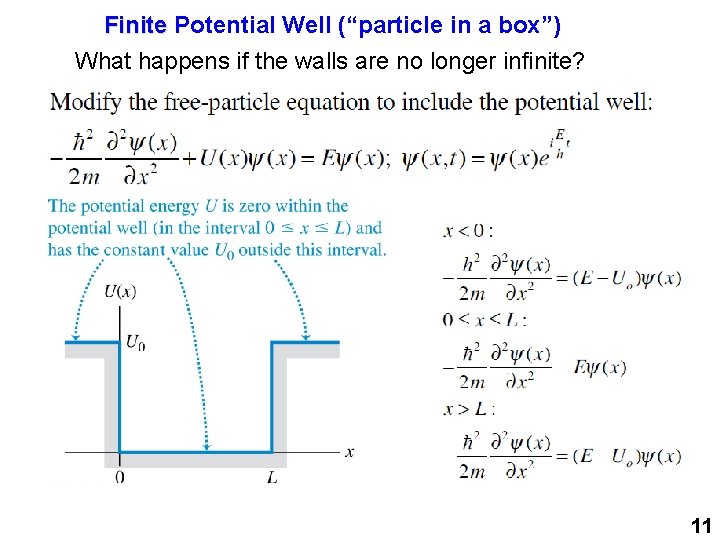
Finite Potential Well (“particle in a box”) What happens if the walls are no longer infinite? 11
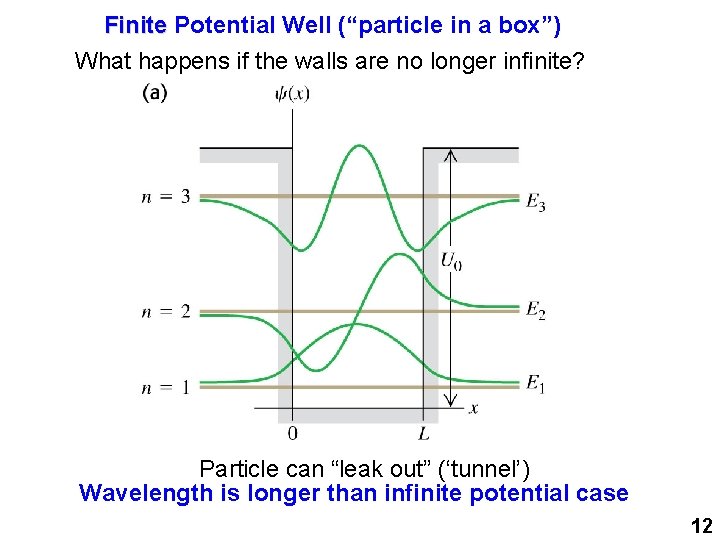
Finite Potential Well (“particle in a box”) What happens if the walls are no longer infinite? Particle can “leak out” (‘tunnel’) Wavelength is longer than infinite potential case 12
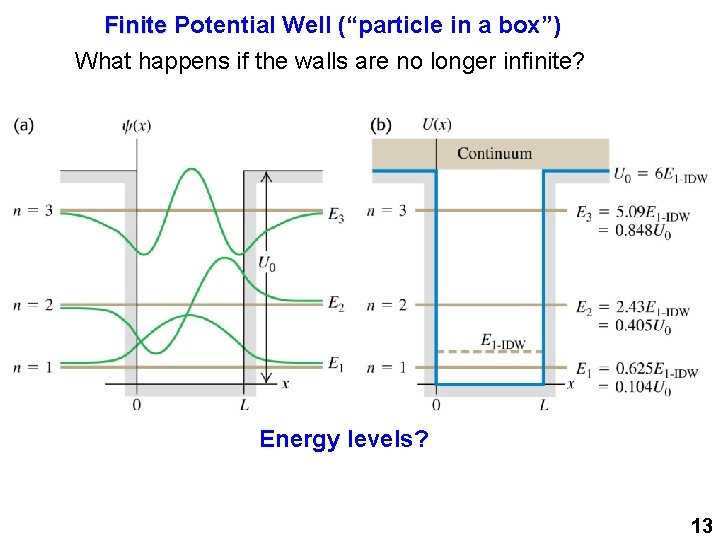
Finite Potential Well (“particle in a box”) What happens if the walls are no longer infinite? Energy levels? 13

Need to solve Schrodinger Eqn: V(x) Energy e. V Eelectron 0 0 Region I L Region II x Region III In Region III … total energy E < potential energy V α is real Positive What functional forms of y(x) work? a. eiαx b. sin(αx) c. eαx d. more than one of these 14

Energy V(x) Eelectron 0 Region I 0 L Region II x Region III In Region III … total energy E < potential energy V α is real Positive Answer is C: eαx … could also be e-αx. Exponential decay or growth Why not eiax? RHS LHS 15
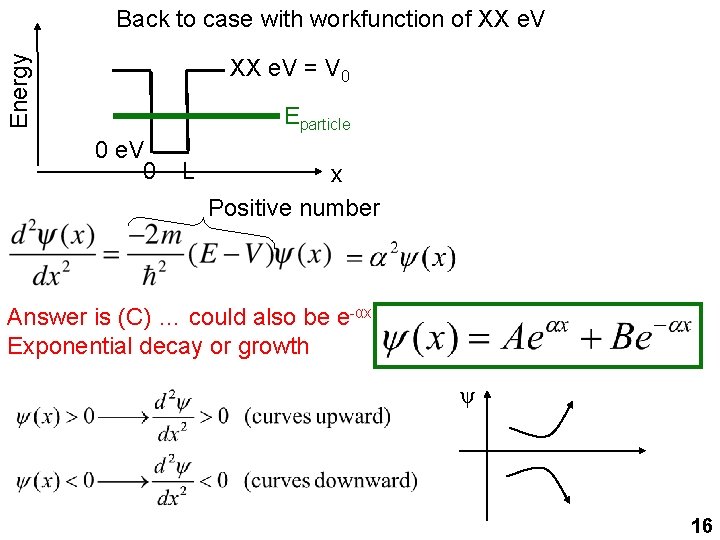
Energy Back to case with workfunction of XX e. V = V 0 Eparticle 0 e. V 0 L x Positive number Answer is (C) … could also be e-αx. Exponential decay or growth ψ 16
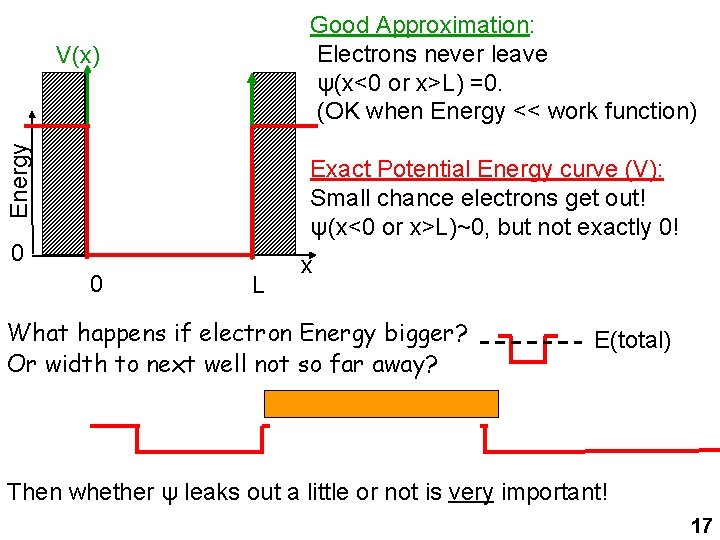
Good Approximation: Electrons never leave ψ(x<0 or x>L) =0. (OK when Energy << work function) Energy V(x) Exact Potential Energy curve (V): Small chance electrons get out! ψ(x<0 or x>L)~0, but not exactly 0! 0 0 L x What happens if electron Energy bigger? Or width to next well not so far away? E(total) Then whether ψ leaks out a little or not is very important! 17

Need to solve for exact Potential Energy curve: V(x): small chance electrons get out of wire ψ(x<0 or x>L)~0, but not exactly 0! Finite Square Well Energy V(x) Work function 0 0 L x Important for thinking about “Quantum tunneling”: Scanning tunneling microscope to study surfaces Radioactive decay with alpha emission. 18
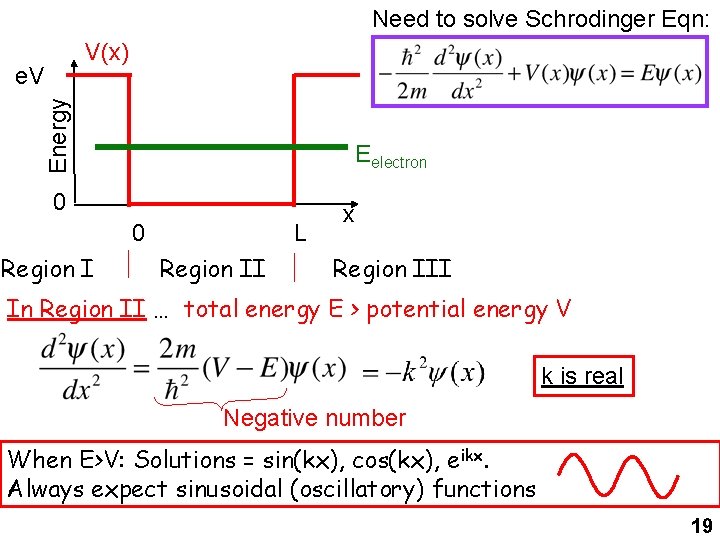
Need to solve Schrodinger Eqn: V(x) Energy e. V Eelectron 0 0 Region I L Region II x Region III In Region II … total energy E > potential energy V k is real Negative number When E>V: Solutions = sin(kx), cos(kx), eikx. Always expect sinusoidal (oscillatory) functions 19
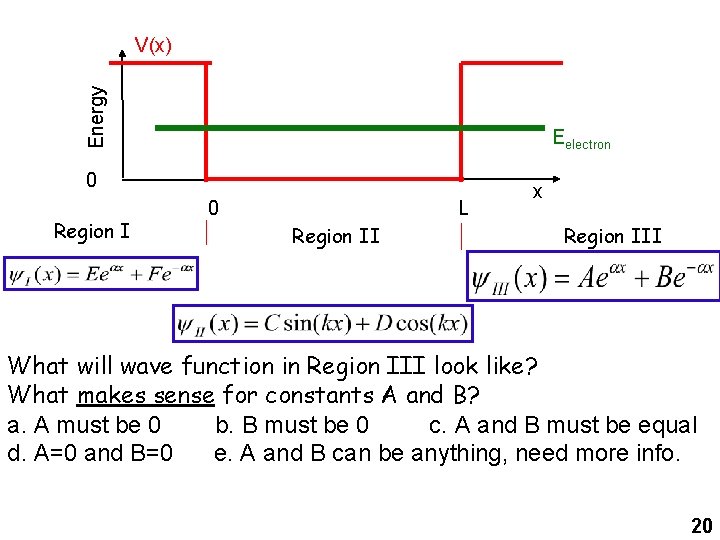
Energy V(x) Eelectron 0 Region I 0 L Region II x Region III What will wave function in Region III look like? What makes sense for constants A and B? a. A must be 0 b. B must be 0 c. A and B must be equal d. A=0 and B=0 e. A and B can be anything, need more info. 20
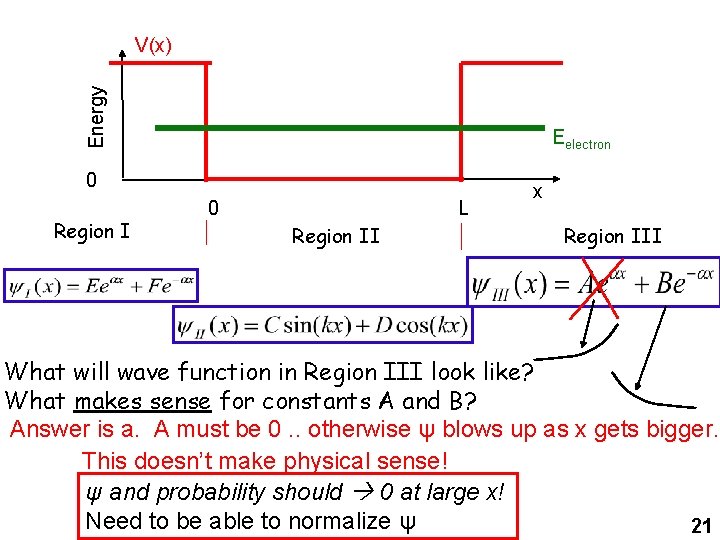
Energy V(x) Eelectron 0 Region I 0 L Region II x Region III What will wave function in Region III look like? What makes sense for constants A and B? Answer is a. A must be 0. . otherwise ψ blows up as x gets bigger. This doesn’t make physical sense! ψ and probability should 0 at large x! Need to be able to normalize ψ 21
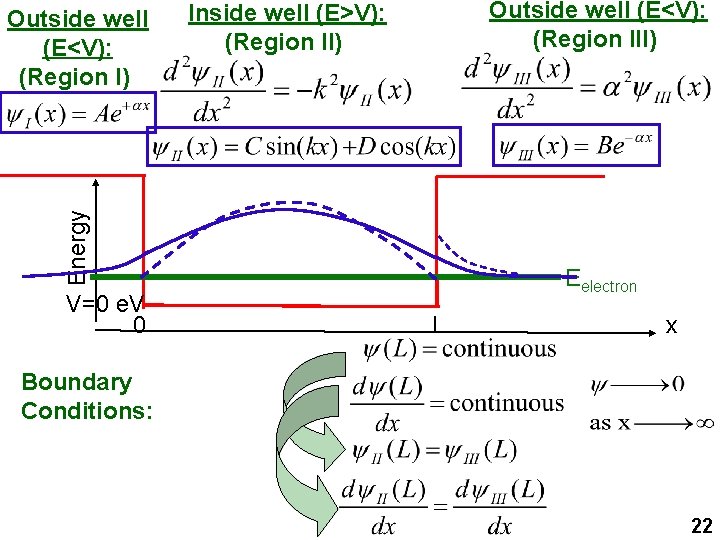
Outside well (E<V): (Region III) Inside well (E>V): (Region II) Energy Outside well (E<V): (Region I) V=0 e. V 0 Eelectron L x Boundary Conditions: 22
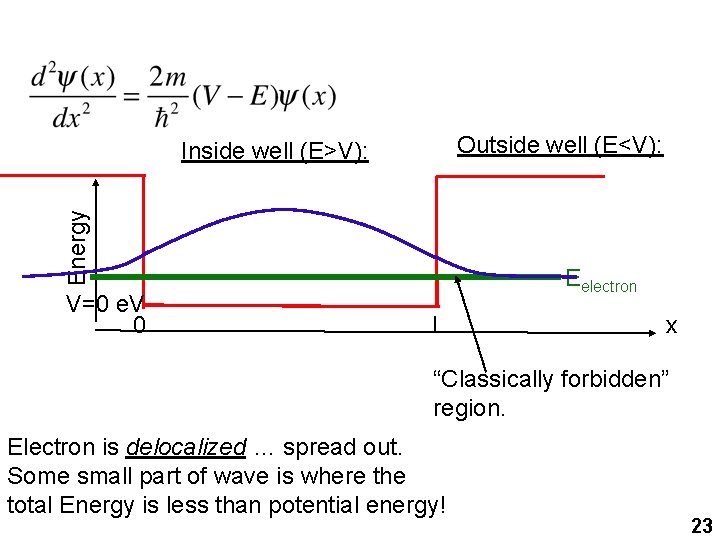
Outside well (E<V): Energy Inside well (E>V): V=0 e. V 0 Eelectron L x “Classically forbidden” region. Electron is delocalized … spread out. Some small part of wave is where the total Energy is less than potential energy! 23
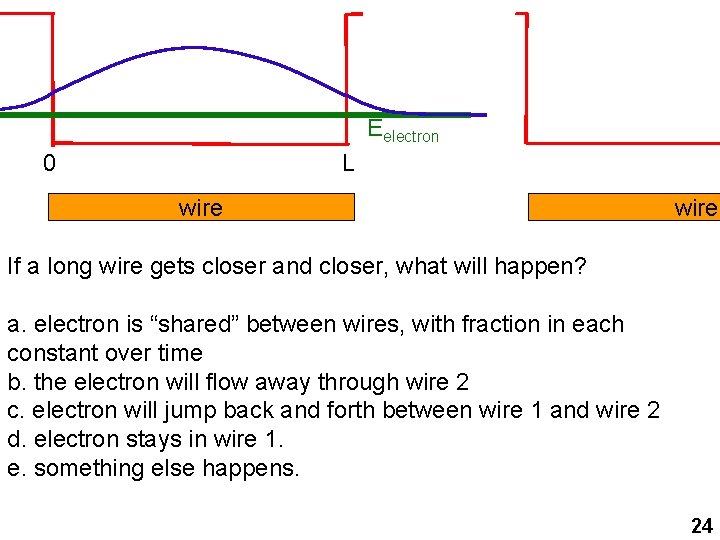
Eelectron 0 L wire If a long wire gets closer and closer, what will happen? a. electron is “shared” between wires, with fraction in each constant over time b. the electron will flow away through wire 2 c. electron will jump back and forth between wire 1 and wire 2 d. electron stays in wire 1. e. something else happens. 24
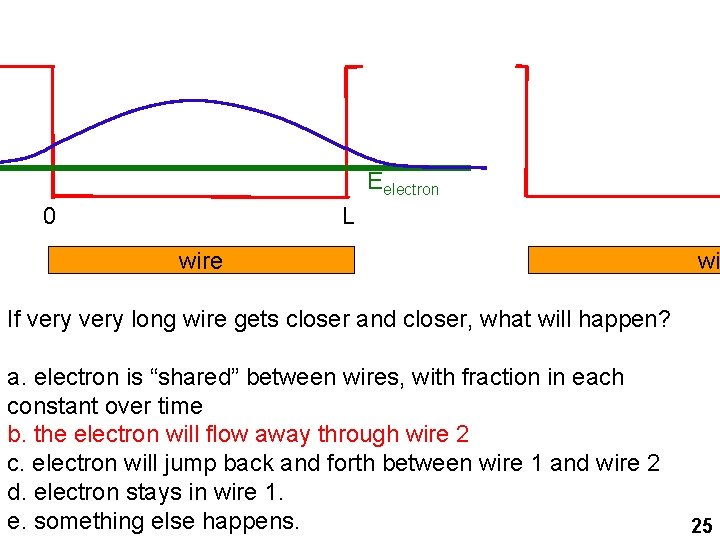
Eelectron 0 L wire wi If very long wire gets closer and closer, what will happen? a. electron is “shared” between wires, with fraction in each constant over time b. the electron will flow away through wire 2 c. electron will jump back and forth between wire 1 and wire 2 d. electron stays in wire 1. e. something else happens. 25
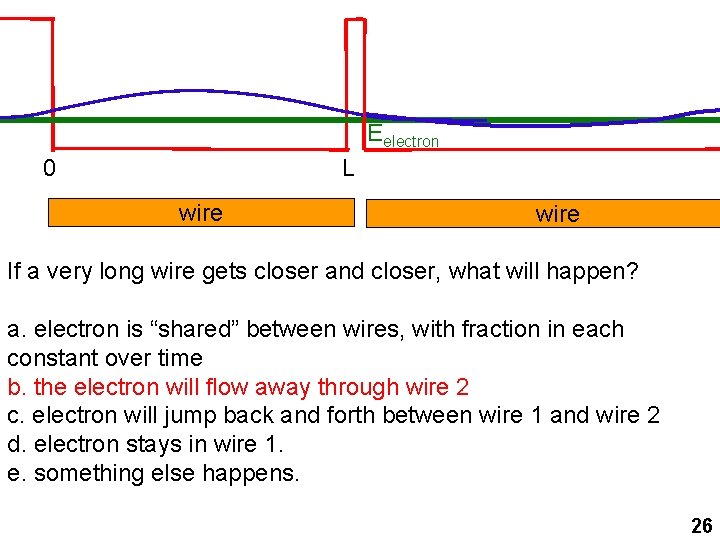
Eelectron 0 L wire If a very long wire gets closer and closer, what will happen? a. electron is “shared” between wires, with fraction in each constant over time b. the electron will flow away through wire 2 c. electron will jump back and forth between wire 1 and wire 2 d. electron stays in wire 1. e. something else happens. 26

Q 26. 1 Compare a particle confined inside a box (infinite potential well) and a particle in a finite potential well, which one has a lower ground state energy? A. Particle in a box (infinite potential well). B. Particle in a finite potential well. C. Both have the same ground state energy 27

Q 26. 1 Compare a particle confined inside a box (infinite potential well) and a particle in a finite potential well, which one has a lower ground state energy? A. Particle in a box (infinite potential well). B. Particle in a finite potential well. C. Both have the same ground state energy Wavefunction can leak out 28

Q 26. 2 29

Q 26. 2 30

For next time • More Quantum Mechanics Ø Read material in advance Ø Concepts require wrestling with material 31
- Slides: 31