PHYS 252 Special Relativity Topic 4 Velocity and

PHYS 252 Special Relativity Topic 4: Velocity and Acceleration Transforms Velocity Transforms The velocity transforms follow directly from the Lorentz transform equations, just as the Newtonian velocity transforms follow from the Galilean transforms. Suppose that an object is moving in both frames of reference as shown in Figure 4 -1. Prime and Unprime measure their own respective velocities for the object. Prime sees the object moving at speed u’ in some direction and Unprime sees the object moving at speed u in a different direction. To find how the speeds and directions compare, it is easiest to first find how the components of the velocities compare. As we did when we derived the Newtonian relativity velocity transforms, we start with the definition of velocity and use the chain rule to write y S y’ S’ v O z z’ (4. 1) ® u’ ® u x O’ x’ Fig. 4 -1 1

We now see the impact of the relativity of time. Unlike in Newtonian relativity, dt/dt’ is no longer unity. From the inverse transform for t, Eq. (3. 2), we find (4. 2) Upon substituting Eq. (4. 2) and the transforms for x’, y’, and z’ into Eqs. (4. 1), and after much algebra, the velocity transformation equations are (4. 3) The ux is not a misprint in the denominator of u’y and u’z. The relative motion of the observers affects the measured components of the object’s velocity that are both parallel and perpendicular to the direction of the relative motion. Recall that this is not the case in Newtonian relativity. There, only the parallel component is affected. The reason for this is once again the relativity of time. Velocity is displacement divided by time. Thus, all components of the velocity are different for the two observers. However, if the relative speed between the two observers is low, these differences are negligible. As we expect, if v/c << 1 then ~ 1 and Eqs. (4. 3) reduce to the Newtonian relativity velocity transforms. (You can verify this. ) The inverse velocity transform equations can easily be obtained from those in Eqs. (4. 3) by swapping primed and unprimed variables and replacing v with –v. 2

Acceleration Transforms We play the same derivative game with the velocity components of the object to obtain the acceleration components of the object measured by the two observers. (4. 4) We transform the velocity components with Eqs. (4. 3) and the time derivative with Eq. (4. 2). We then do lots of algebra. The results that we get are (4. 5) We see that the two observers do not measure the same acceleration for the object as in Newtonian relativity. However, the laws of physics still work in both frames. 3

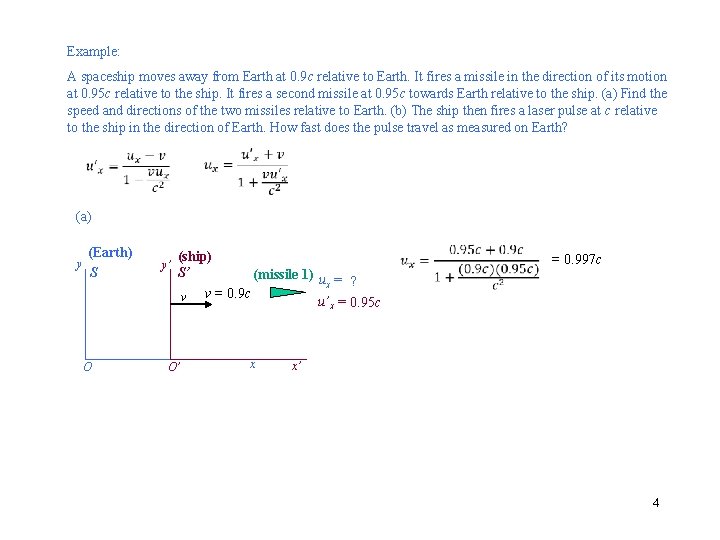
Example: A spaceship moves away from Earth at 0. 9 c relative to Earth. It fires a missile in the direction of its motion at 0. 95 c relative to the ship. It fires a second missile at 0. 95 c towards Earth relative to the ship. (a) Find the speed and directions of the two missiles relative to Earth. (b) The ship then fires a laser pulse at c relative to the ship in the direction of Earth. How fast does the pulse travel as measured on Earth? (a) y (Earth) S O y’ (ship) S’ (missile 1) u = ? x v = 0. 9 c v u’x = 0. 95 c O’ x = 0. 997 c x’ 4

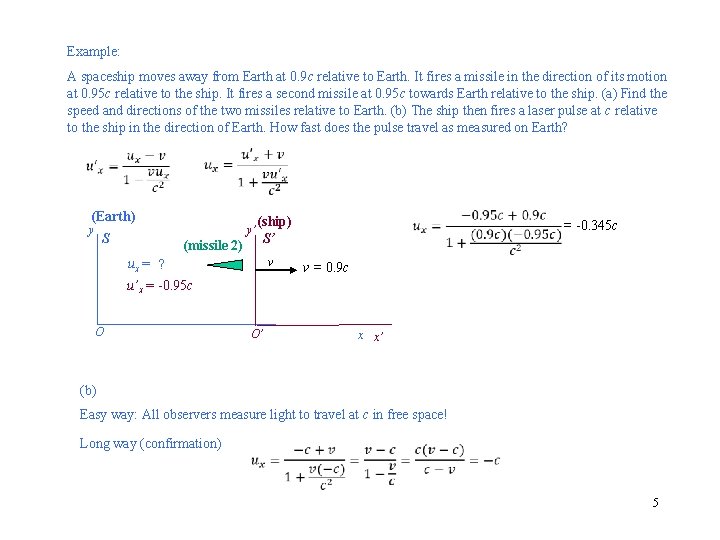
Example: A spaceship moves away from Earth at 0. 9 c relative to Earth. It fires a missile in the direction of its motion at 0. 95 c relative to the ship. It fires a second missile at 0. 95 c towards Earth relative to the ship. (a) Find the speed and directions of the two missiles relative to Earth. (b) The ship then fires a laser pulse at c relative to the ship in the direction of Earth. How fast does the pulse travel as measured on Earth? (Earth) y S y’ (missile 2) (ship) S’ v ux = ? = -0. 345 c v = 0. 9 c u’x = -0. 95 c O O’ x x’ (b) Easy way: All observers measure light to travel at c in free space! Long way (confirmation) 5