PHYS 221 EXAM 2 REVIEW Reminders NO SI








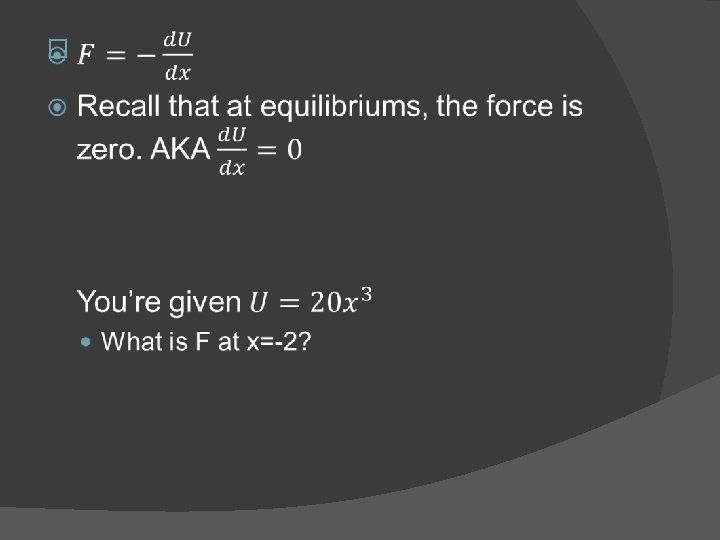




















- Slides: 41

PHYS 221 EXAM 2 REVIEW

Reminders: � NO SI THURSDAY!!

Exam Overview “Approximately 1/3 of the problems will stress understanding of the physics concepts, whereas the remainder will be numerical problems to test ability to apply these concepts. ” -Syllabus 27 Questions

Statistical Breakdown of Exam 2 26% Energy � 17% Collisions (+Momentum) � 46% Rotational (Center of mass, moment of inertia, statics, angular momentum, torque) � 10% Gravitational � Let’s put some analogies to work: Not knowing gravitation would be like losing 3 fingers Not knowing rotational is like losing a heart or both lungs


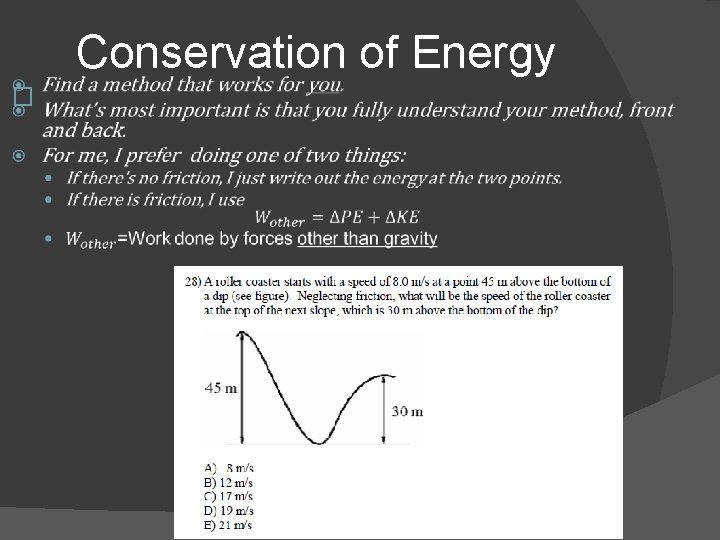
Energy � Conservation of Energy �Conservative/Non-conservative �Potential Energy � Springs � Collisions � Rotational � Gravitational Force/PE


Springs � A 10 kg mass hits a spring at a speed of 50 m/s. The spring has k=30 N/m. �How far will the spring be compressed? �What will the PE of the spring be when it is fully compressed? �What will the PE of the spring be when it is halfway compressed?

� Conservation of Energy

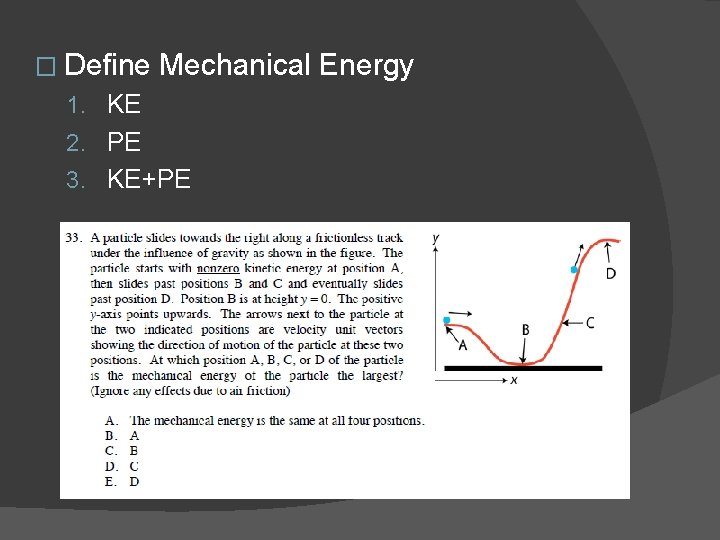
� Define Mechanical Energy 1. KE 2. PE 3. KE+PE

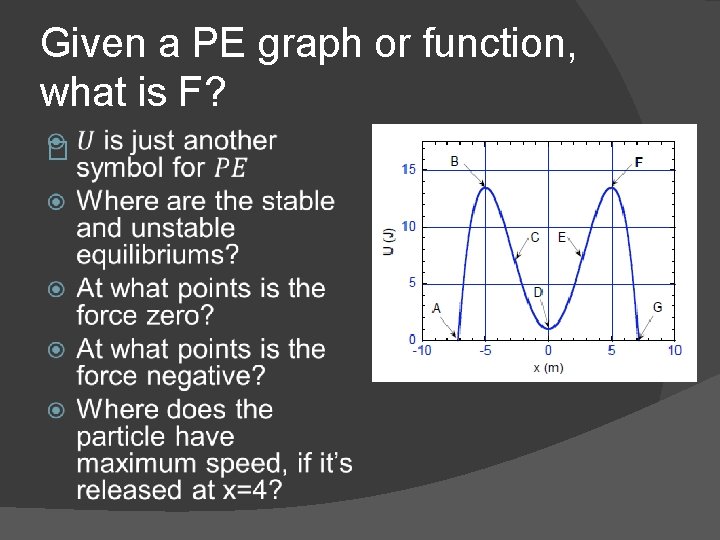
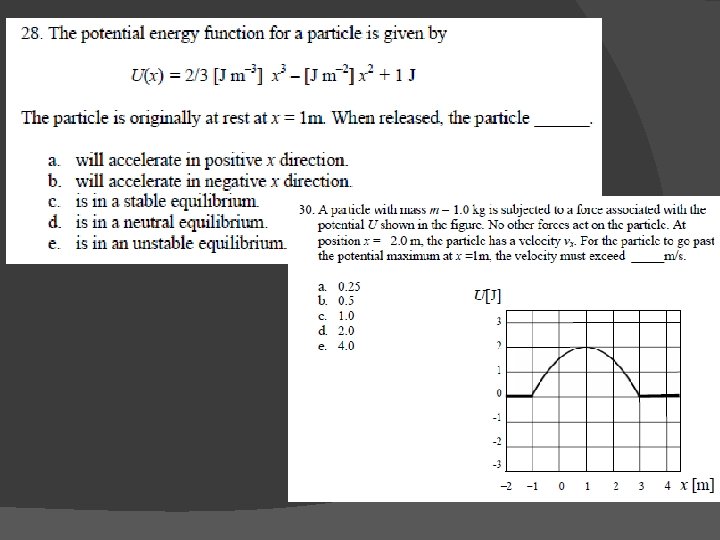
Given a PE graph or function, what is F? �
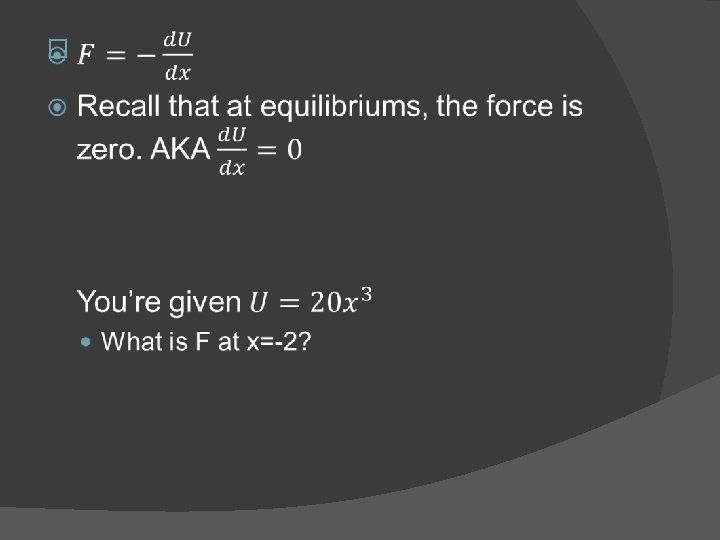


Conservative Forces vs. Non-conservative Forces � Conservative �Always associated with some PE �Work doesn’t depend on path taken �Examples: Gravity, Electrostatic � Not Conservative �PE doesn’t exist �Work does depend on path �Examples: Friction, Air resistance

Collisions �

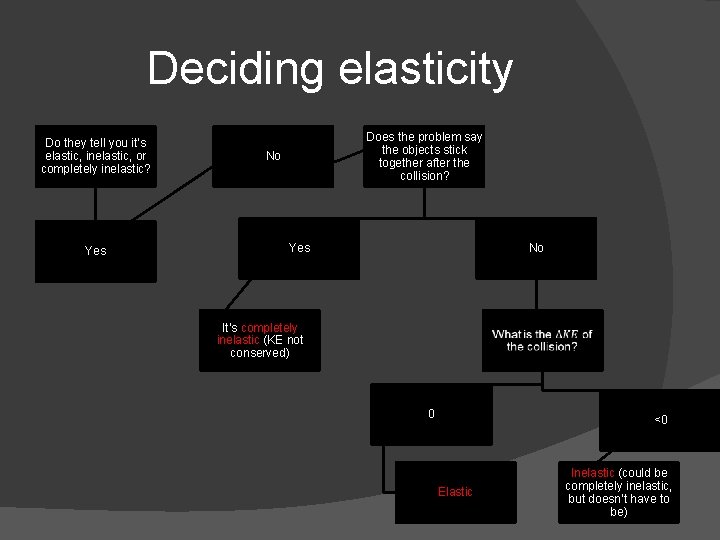
Deciding elasticity Do they tell you it’s elastic, inelastic, or completely inelastic? Yes Does the problem say the objects stick together after the collision? No Yes No It’s completely inelastic (KE not conserved) 0 <0 Elastic Inelastic (could be completely inelastic, but doesn’t have to be)

Is Momentum Conserved in a Collision � In this course, YES, ALWAYS!


Impulse �

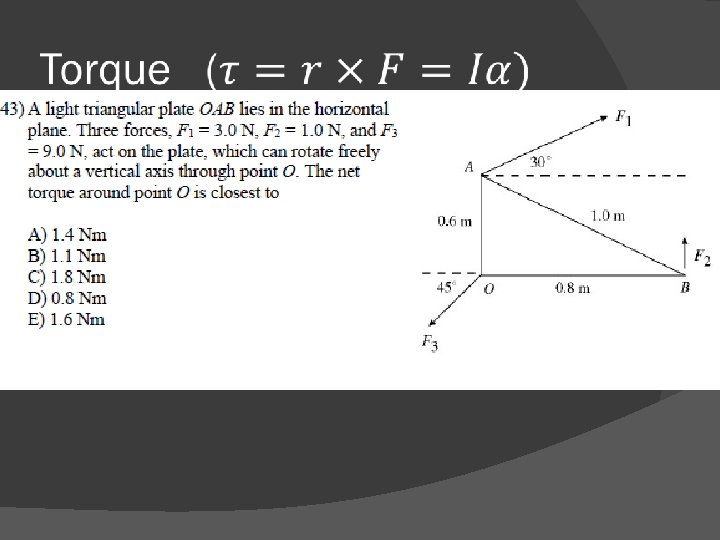
Rotational �

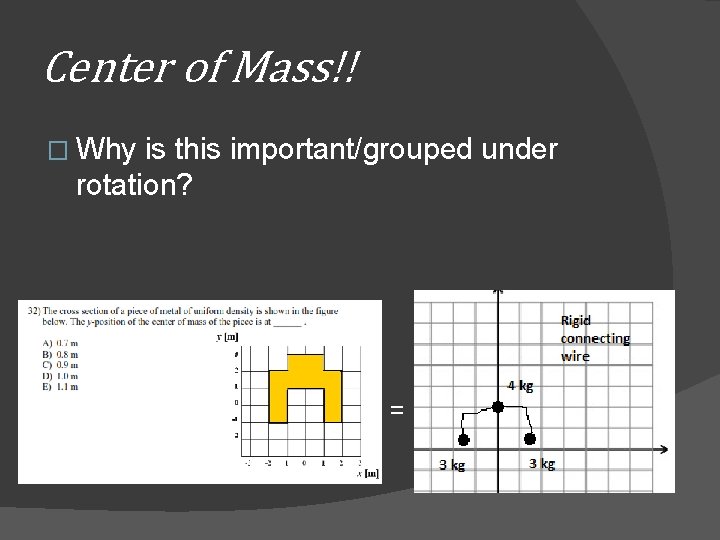
Center of Mass!! � Why is this important/grouped under rotation? =

Solve… � Mathematically… � Intuitively �Do circular or non-circular go faster down hills?

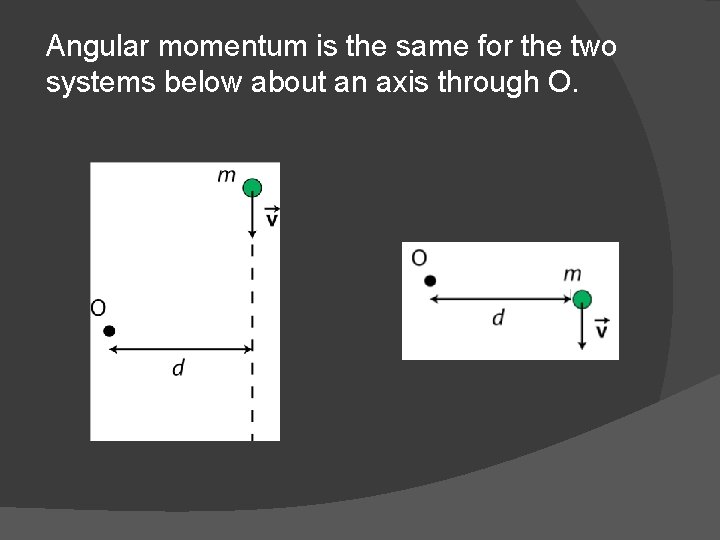
Angular momentum is the same for the two systems below about an axis through O.

Discrete/Continuous…which formula should I use?

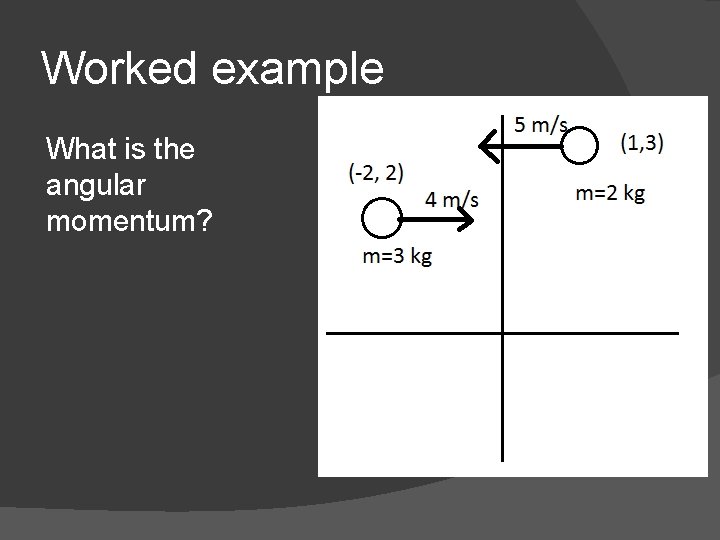
Worked example What is the angular momentum?


� If net torque is zero, an object can still be moving. �In fact, the object can even be accelerating! �However, the angular acceleration must be zero, and the angular velocity must be constant.

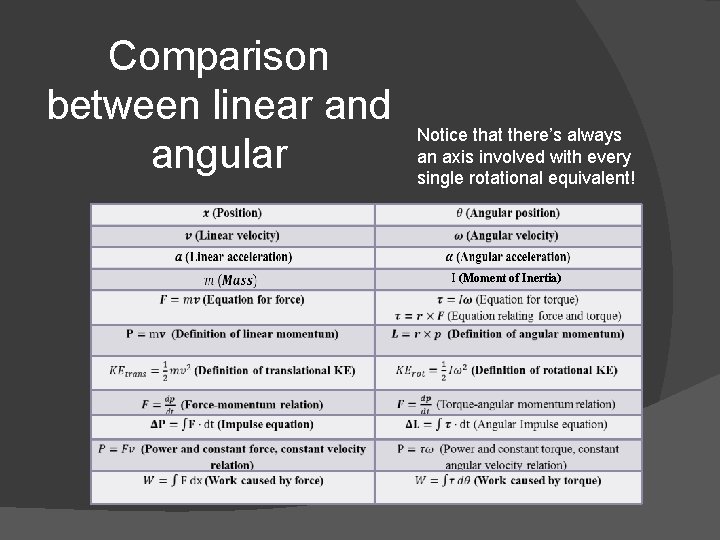
Comparison between linear and angular Notice that there’s always an axis involved with every single rotational equivalent! I (Moment of Inertia)

Statics � Can be solved in 2 minutes � Strategy: Generally, use conservation of angular momentum first!


Both discrete and continuous!

� Is Momentum Conserved? � Is Angular Momentum Conserved?

Gravitation �

Examples: A planet is in a circular orbit around a star. The mass of the star is 5 * 1028 kg. If the period of the planet’s orbit is 1. 00 * 105 s, then the orbital radius of the planet around the star is ____ m. The centers of two small uniform spherical bodies are separated by a distance d and the magnitude of the attractive gravitational force of one on the other is F. If the distance between the centers of the bodies decreases to d/2, the magnitude of the force of one on the other becomes ____.


A 1. 53 -kg mass hangs on a rope wrapped around a disk pulley of mass 7. 07 kg and radius 66. 0 cm. The rope does not slip on the pulley. � What is the angular acceleration of the pulley? � If the block has fallen 0. 8 m, what is the speed of the block at that time? (Two ways to solve this)

Other Concepts � Magnitude of Forces, vectors, etc…

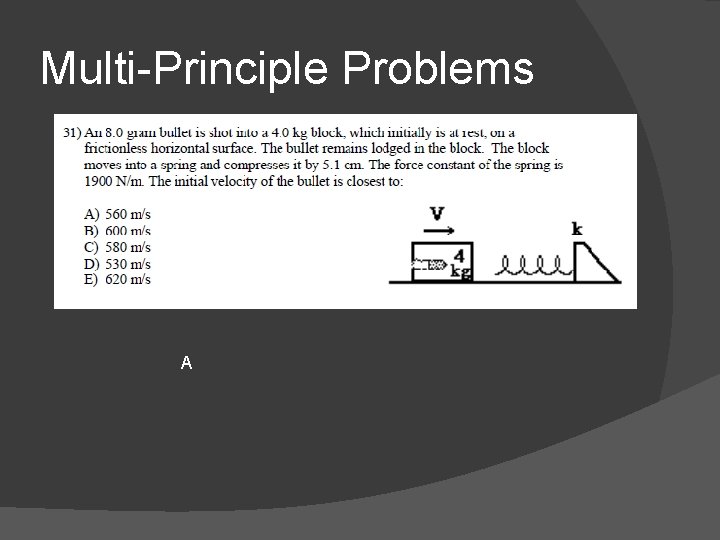
Multi-Principle Problems A

Trickier Problems

