Phylognetic trees What to look for and where

Phylognetic trees: What to look for and where? Lessons from Statistical Physics Elchanan Mossel, U. C. Berkeley and Microsoft Research mossel@stat. berkeley. edu, www. stat. berkeley. edu/~mossel/ 1/8/2022 1

Statistical physics • Statistical physics is a sub-field of mathematical physics studying complex systems with simple microscopic interactions. • The Ising model on a graph G=(V, E) is a probability measure (“Gibbs distribution”) on the space of configurations σ : V {-1, 1} such that P[σ] is given by: • exp(Σ(v, w) ε E σ(v)σ(w)/T)/Z = exp( Σ(v, w) ε E σ(v)σ(w))/Z • Or, Weight( ) ~ exp( # { u ~ v : (u) = (v) } ) • Traditionally studied on cubes in Zd. 1/8/2022 The Ising model on 200 x 200 grid 2

Statistical physics - intuition • The Ising model on the nxn grid is given by: • exp(Σ(v, w) ε E σ(v)σ(w)/T)/Z = exp( Σ(v, w) ε E σ(v)σ(w))/Z • We expect that: • T small, large ) strong correlations: – Corr( boundary, 0) > > 0 for all n. • T large, small ) weak correlations: 2 n 0 – Corr( boundary, 0) ! 0 as n ! 1. boundary • Onsager (1944) proved it where • Critical = c = ln(1+21/2)/2 • For most other graphs, we know very little 1/8/2022 The Ising model on 200 x 200 grid = c 3

Statistical physics on trees • The Ising model on a tree T=(V, E) is given by: • exp( Σ(v, w) ε E (v, w) (v) (w))/Z • It is equivalent to the following model: • Let r be a root (chosen arbitrarily). • Let (r) = § 1 with probability ½ and for • Each edge (u, v) directed away from the root, let: – (v) = (u) with probability (u, v). – (v) is independent § 1 otherwise. • + (u, v) = ( e (u, v)-e- (u, v) )/ (e (u, v)+e- (u, v)) + + + 1/8/2022 + - - + + + 4

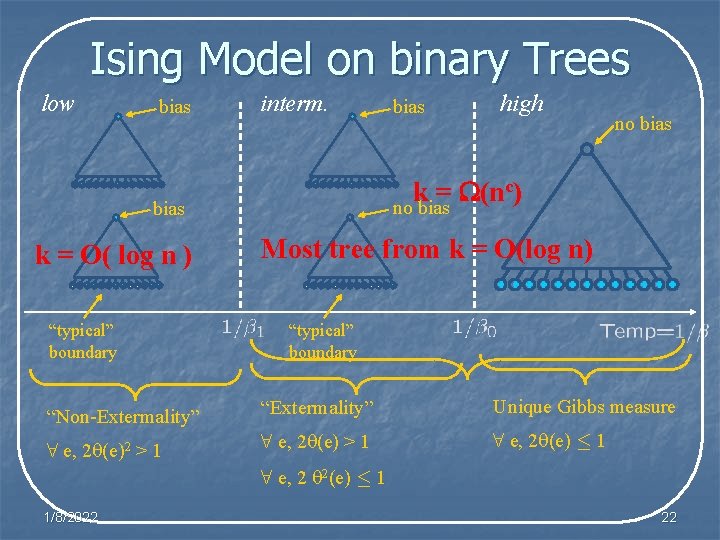
Ising Model on binary Trees low bias interm. high no bias “typical” boundary “Non-Extermality” “Extermality” Unique Gibbs measure 8 e, 2 (e)2 > 1 8 e, 2 (e) · 1 8 e, 2 2(e) · 1 1/8/2022 5

Statistical physics on trees: History • Uniqueness studied by Bethe (1930’s). • Extremality phase more recently Spitzer 75, Higuchi 77, Bleher-Ruiz-Zagrebnov 95, Evans-Kenyon-Peres-Schulman 2000, Ioffe 99, M 98, Haggstrom-M 2000, Kenyon-M-Peres 2001, Martinelli-Sinclair Weitz- 2003, Martin-2003 • Many problems are still open. • Extremality has rich connections with – Noisy computation/communication [von-Neumann 53, Evans-Shculmann 00, …] – Mixing of Markov chains [Berger-Kenyon-Mossel. Peres 01, Martinelli-Sinclair-Weitz 05] – Spinglasses and Random Sat problems [Parisi, Mezard, Montanari; Mezard-Montanari 06] 1/8/2022 6

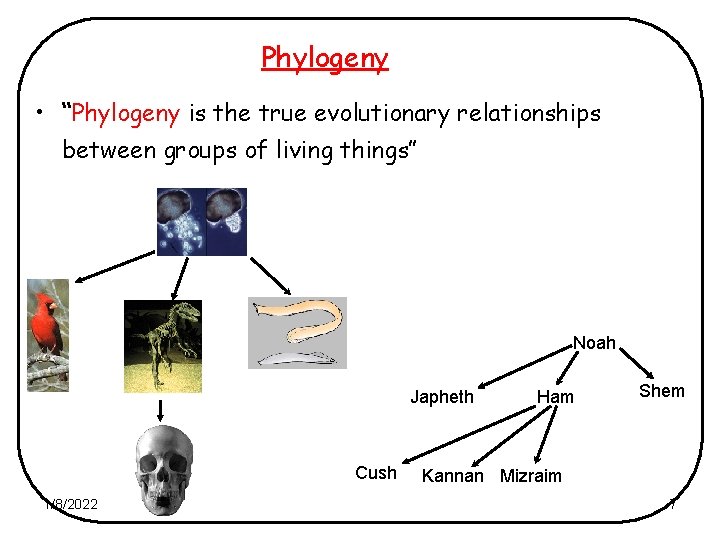
Phylogeny • “Phylogeny is the true evolutionary relationships between groups of living things” Noah Japheth Cush 1/8/2022 Ham Shem Kannan Mizraim 7

History of Phylogeny • Intuitively: : “animal kingdom” or “plant kingdom. ” • More scientifically: morphology, fossils, etc. Darwin … • But: Is a human more like a great ape or like a chimpanzee? No brain, Can’t move Stupid Walks Stupid Swims Stupid Flies 1/8/2022 Too smart Barely moves 8

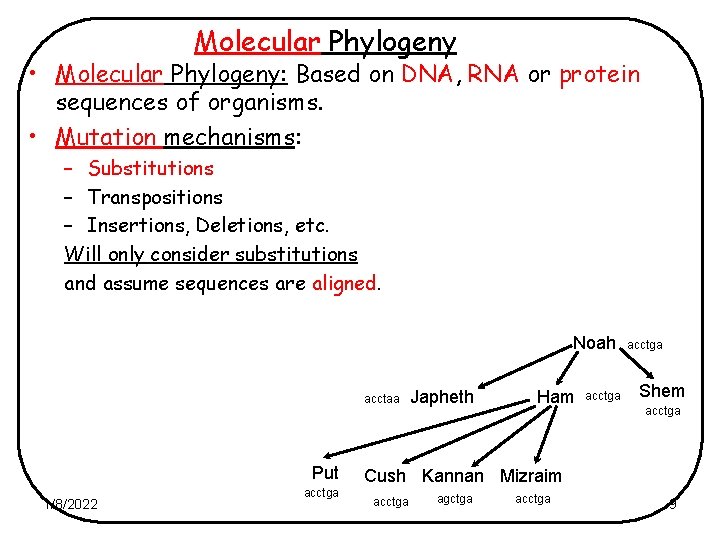
Molecular Phylogeny • Molecular Phylogeny: Based on DNA, RNA or protein sequences of organisms. • Mutation mechanisms: – Substitutions – Transpositions – Insertions, Deletions, etc. Will only consider substitutions and assume sequences are aligned. Noah acctaa Put 1/8/2022 acctga Japheth Ham acctga Shem acctga Cush Kannan Mizraim acctga agctga acctga 9

Simplifying assumptions: models • Assumption: Letters of sequences (“characters”) evolve independently and identically. • CFN model: The first stochastic model invented by Cavender, Farris and Neyman (70 s): – Let (r) = § 1 with probability ½ and for – Each edge (u, v) directed away from the root, let: – (v) = (u) with probability (u, v). – (v) is independent § 1 otherwise. This is exactly the Ising model on the evolutionary tree! • Dictionary: {A, C} = + (Pyrimidine group) {G, T} = - (Purine group). • Some results can be generalized to other models. 1/8/2022 10

Simplifying assumptions: trees • Assumption 1: Evolution is on a tree. u • Assumption 2: Trees are binary -- All internal degrees are 3. Me ’ v • Given a set of species (labeled vertices) X, an X-tree is a tree which has X as the set of leaves. • Two X-trees T 1 and T 2 are identical if there’s a graph isomorphism between T 1 and T 2 that is the identity map on X. • Most results to trees all of whose internal degrees are at least 3. 1/8/2022 u Me’’ w w d a c b d a b c c a b d 11

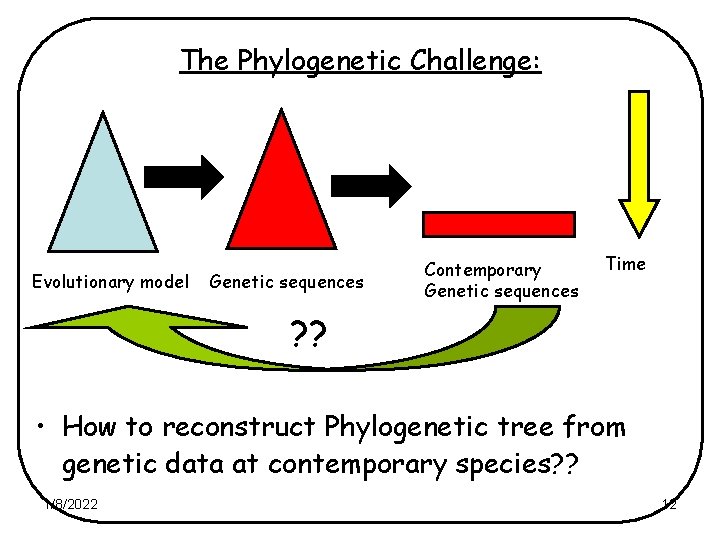
The Phylogenetic Challenge: Evolutionary model Genetic sequences Contemporary Genetic sequences Time ? ? • How to reconstruct Phylogenetic tree from genetic data at contemporary species? ? 1/8/2022 12

Phylogeny • Tree is unknown. • Given sequences at the leaves of the tree. • Want to reconstruct the tree (un-rooted). • How “hard” is it as a function of – n = “size of tree” = # leaves. – k = length of sequences. 1/8/2022 13

Phylogeny 1/8/2022 14

n and k • Interested to know k = #characters needed to reconstruct the tree with n = #leaves. Length of sequence! • Erdos-Steel-Szekeley-Warnow 96: • If < (e) < 1 - for all e. • Tree can be recovered from – Sequences of length k = nc. – In polynomial time. • Question: How about shorter sequences? • Previously, best lower bound on sequence length is k = (log n). • However, in practice: – Sometimes hard to find long sequences. – Short sequences often suffice. 1/8/2022 15

Lesson 1: Phylogenetic lower bound forgetful trees • Th[M 2004; Trans AMS]: • If 2 2(e) < 1 for all e then we show • A lower bound on sequence length of k = nc, where • c > 0 is a function of =maxe (e) and • c ! 1 as ! 0. • Th [M 2003; JCB] • Similar theorem for general mutation models if mutation rates are high. • Proofs are easy. 1/8/2022 16

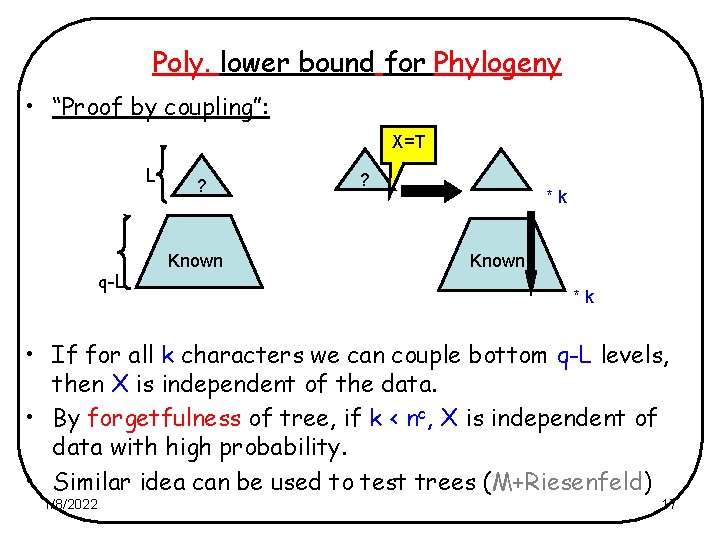
Poly. lower bound for Phylogeny • “Proof by coupling”: X=T L q-L ? Known ? *k Known *k • If for all k characters we can couple bottom q-L levels, then X is independent of the data. • By forgetfulness of tree, if k < nc, X is independent of data with high probability. • Similar idea can be used to test trees (M+Riesenfeld) 1/8/2022 17

Lesson 2: Recent history is easy • In the proof of lower bound, the “deep convergences” were hard to reconstruct. • Theorem [M 04]: • If < (e) < 1 - for all e, then • “most of the tree” can be reconstructed from • sequences of length k = O(log n). • “most of tree” : = a forest F such that the true tree is obtained from F by adding o(n) edges. • Result were refined + experiments in [Daskalakis. Hill-Jaffe-Miahescu-Mossel-Rao] • Proof is *not* easy – based on Distorted Metrics. 1/8/2022 18

Lesson 3: Species that remember their past can reconstruct their history. • Thm [Daskalakis-Mossel-Roch; To appear STOC 06]: • If 2 2(e) > 1 for all e then • The tree can be recovered with high probability from sequences of length k = O( log n ). • Solves M. Steel’s “Favourite conjecture” • Builds on: [M 2004; Trans AMS] • Hard proof: Mixes probability, algorithms, statistical physics. 1/8/2022 19

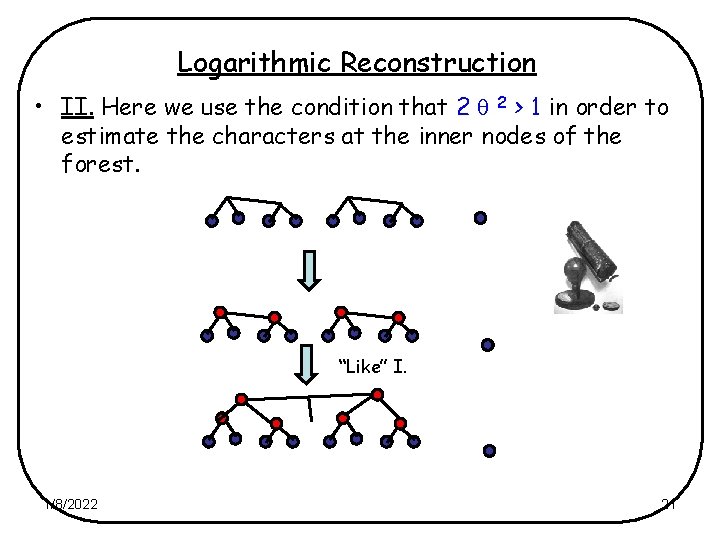
Proof Sketch: Logarithmic reconstruction • Two parts of the proofs: – I. Statistical / algorithmic. – II. Probability / statistical physics. • By Forest result we may recover a forest containing 90% of the edges of the tree from O(log n) samples. – Doesn’t use the 2 2 > 1 1/8/2022 20

Logarithmic Reconstruction • II. Here we use the condition that 2 2 > 1 in order to estimate the characters at the inner nodes of the forest. “Like” I. 1/8/2022 21

Ising Model on binary Trees low bias interm. “typical” boundary high no bias c) k = (n no bias k = O( log n ) bias Most tree from k = O(log n) “typical” boundary “Non-Extermality” “Extermality” Unique Gibbs measure 8 e, 2 (e)2 > 1 8 e, 2 (e) · 1 8 e, 2 2(e) · 1 1/8/2022 22

Many more challenges to come … • We know very little … • We don’t understand methods used in practice: • Maximum Likelihood (NP hard on arbitrary data; [Chor -Tuller 05; Roch 05]) • Markov Chain Monte Carlo (Can be exponentially slow on mixtures; M-Vigda 05). • In what sense Parsimony = Maximum – Likelihood? (2 Conjectures by Steel) • Other mutation models: rates across sites, gene order etc. • + all the problems on Gibbs measures on trees 1/8/2022 23