Phylogenetics Workhop 16 18 August 2006 Distance Based
Phylogenetics Workhop, 16 -18 August 2006 Distance Based Methods for estimating phylogenetic trees Barbara Holland Cat Dog Rat Cat Rat 1 Dog 3 Rat 4 5 Cow 6 7 2 6 2 1 4 Dog Cow

Overview How do we get distance data? n Observed vs. actual distances n Correcting for hidden changes n Not all distances are “tree-like” n Tree building: clustering methods n ¨ UPGMA ¨ Neighbor-joining n Tree building: optimality criteria ¨ Least Squares
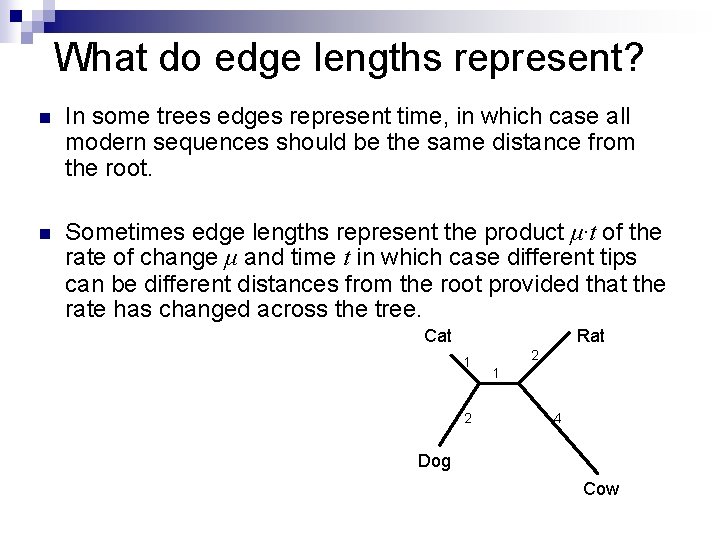
What do edge lengths represent? n In some trees edges represent time, in which case all modern sequences should be the same distance from the root. n Sometimes edge lengths represent the product μ∙t of the rate of change μ and time t in which case different tips can be different distances from the root provided that the rate has changed across the tree. Cat Rat 1 2 2 1 4 Dog Cow

Distance matrices n n There are many ways of building phylogenetic trees, one family of methods uses a distance matrix as a starting point. A distance matrix is a table that indicates pairwise dissimilarity, for instance. . . A B C D Cat Dog Rat Cow Cat 0 2 4 7 B 400 - - - Dog 2 0 5 6 C 300 - - Rat 4 5 0 3 D 250 150 250 - Cow 7 6 3 0 E 250 500 200

Properties of distances n n d(x, x) = 0 d(x, y) = d(y, x) d(x, y) + d(y, z) >= d(x, z) (the triangle inequality) The distances used in phylogenetics always have the first two properties but sometimes not the third.

I want to build a tree - will any old distances do? Not all distances will be suitable for building trees. n Tree-building methods do not discriminate, they will return a tree regardless of whether you give them roadmap distances or distances based on a sequence alignment. n Some distances are perfectly “tree-like”. n
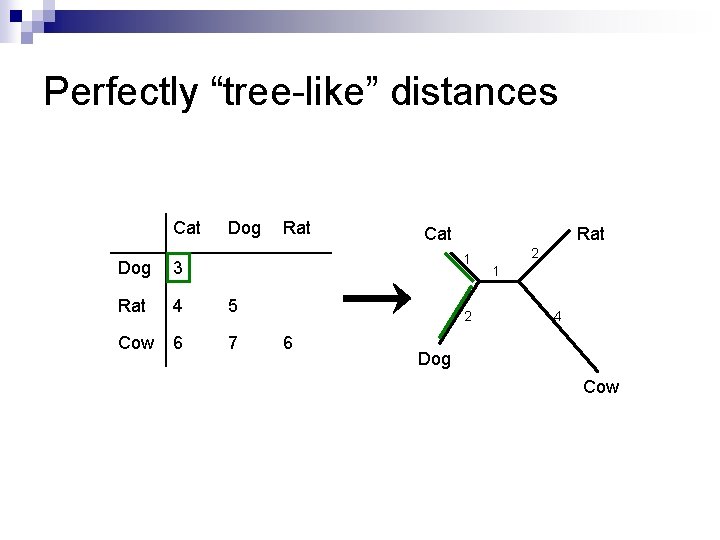
Perfectly “tree-like” distances Cat Dog Rat Cat Rat 1 Dog 3 Rat 4 5 Cow 6 7 2 6 2 1 4 Dog Cow
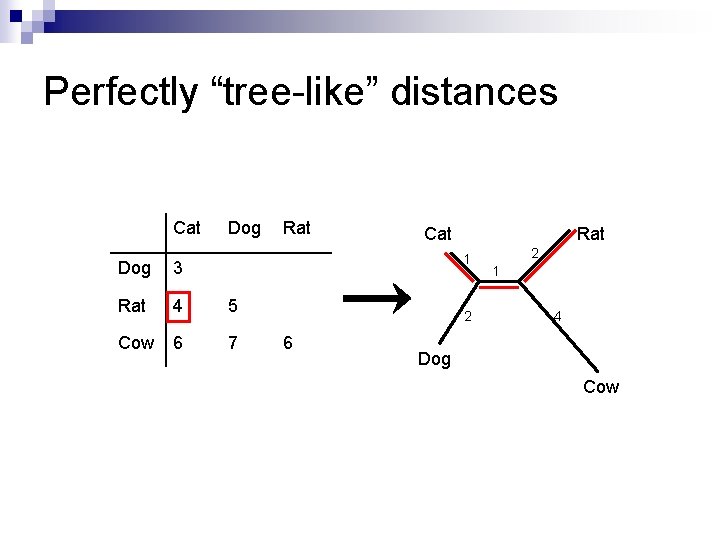
Perfectly “tree-like” distances Cat Dog Rat Cat Rat 1 Dog 3 Rat 4 5 Cow 6 7 2 6 2 1 4 Dog Cow
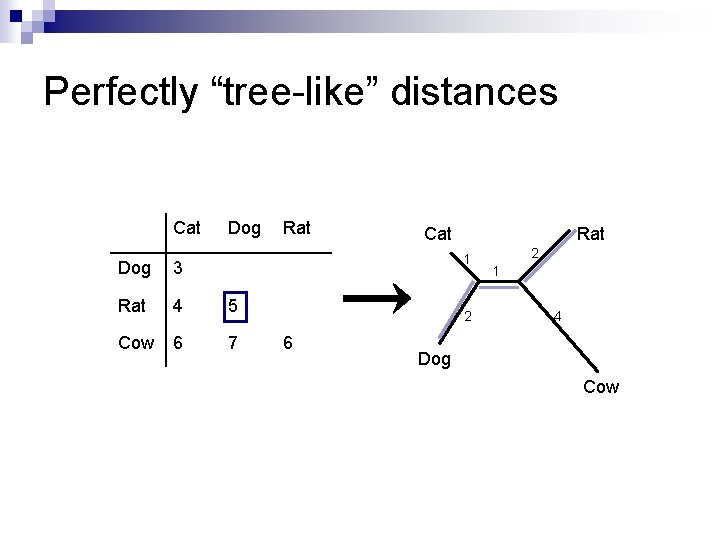
Perfectly “tree-like” distances Cat Dog Rat Cat Rat 1 Dog 3 Rat 4 5 Cow 6 7 2 6 2 1 4 Dog Cow
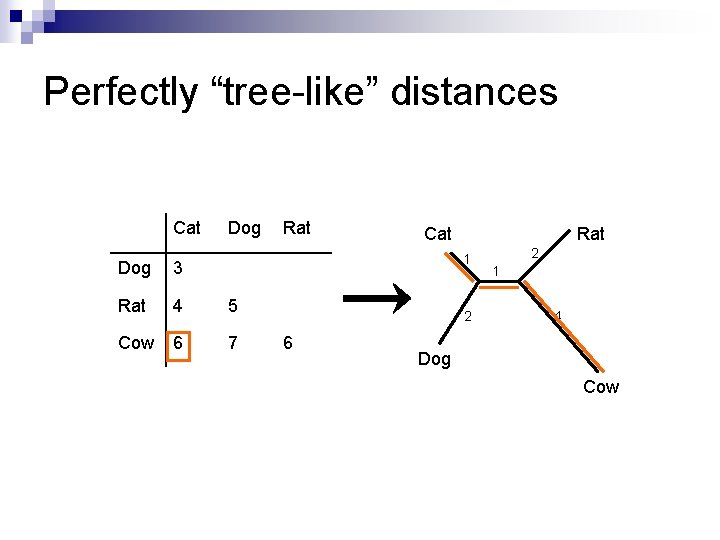
Perfectly “tree-like” distances Cat Dog Rat Cat Rat 1 Dog 3 Rat 4 5 Cow 6 7 2 6 2 1 4 Dog Cow
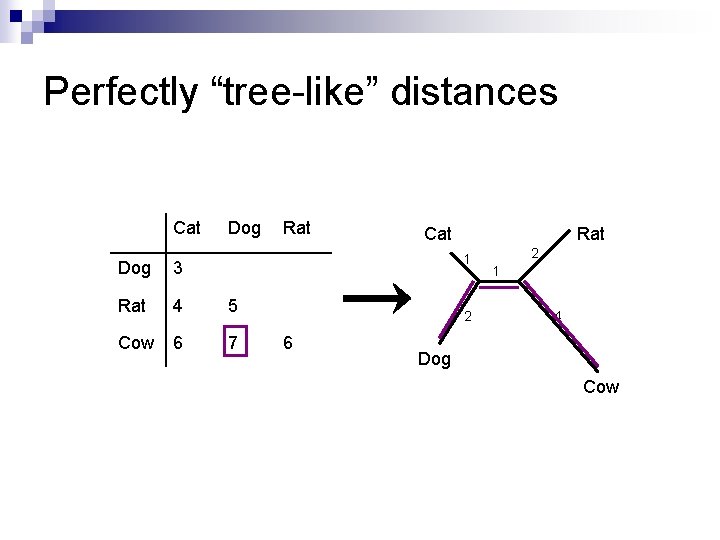
Perfectly “tree-like” distances Cat Dog Rat Cat Rat 1 Dog 3 Rat 4 5 Cow 6 7 2 6 2 1 4 Dog Cow
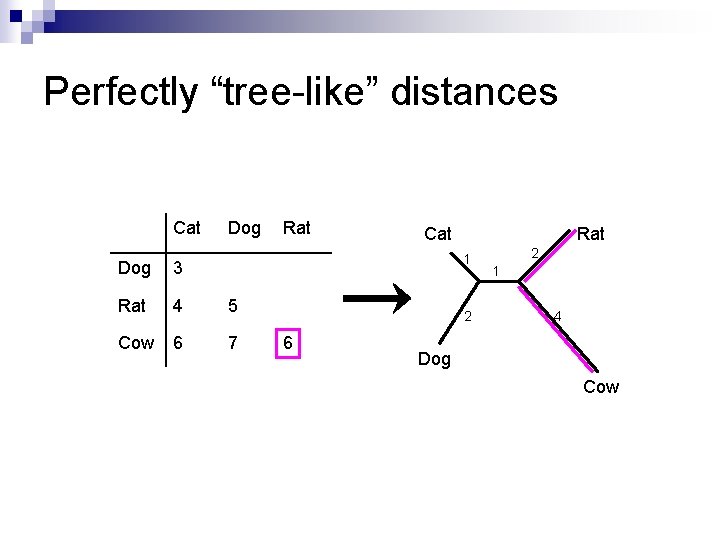
Perfectly “tree-like” distances Cat Dog Rat Cat Rat 1 Dog 3 Rat 4 5 Cow 6 7 2 6 2 1 4 Dog Cow

The 4 -Point Condition Distances that fit exactly on a tree can be characterised by a condition on any quartet i, j, k, l (i. e. it must hold true for any 4 taxa). n We write d(x, y) for the distance between x and y. Given 4 taxa i, j, k, l, of the 3 sums n § § § d(i, j) + d(k, l) d(i, k) + d(j, l) d(i, l) + d(j, k) The largest two are equal. n Distances with this property are called additive, because the weights on the paths along the tree add up to the values in the distance matrix.

Why is this true of tree-like distances? i k i k j l j l d(i, j)+d(k, l) < d(i, k)+d(j, l) = d(i, l)+d(j, k)

Clock-like distances An even stricter condition on distances is that they fit on a clock-like tree. n Distances with this property are called ultrametric. time n d(i, k) = d(j, k) > d(i, j) i j k

Where do we get distances from? n n Distances can be derived from Multiple Sequence Alignments (MSAs). The most basic distance is just a count of the number of sites which differ between two sequences divided by the sequence length. These are sometimes known as p-distances. Cat Dog Rat Cow Cat 0 0. 2 0. 4 0. 7 Dog 0. 2 0 0. 5 0. 6 Rat 0. 4 0. 5 0 0. 3 Cow 0. 7 0. 6 0. 3 0 ATTTGCGGTA ATCTGCGATA ATTGCCGTTT TTCGCTGTTT

Other sources of distances n Immunological data ¨ n DNA/DNA hybridization ¨ n Similarity between proteins A and B can be assessed by how well the immune system responds to B after already having seen A. more similar DNA hybrids "melt" at higher temperatures Fragment length polymorphism “Chop DNA up” using restriction enzymes. ¨ Amplify some fragments usign PCR ¨ Run the fragments out on an electrophoretic gel ¨ Compare profiles of different genomes ¨ n BLAST scores

Observed distances usually underestimate the true number of changes ATTTGCGATA Actual Changes = 2 Observed Changes = 2 ATTTGCGGTA ATCTGCGATA
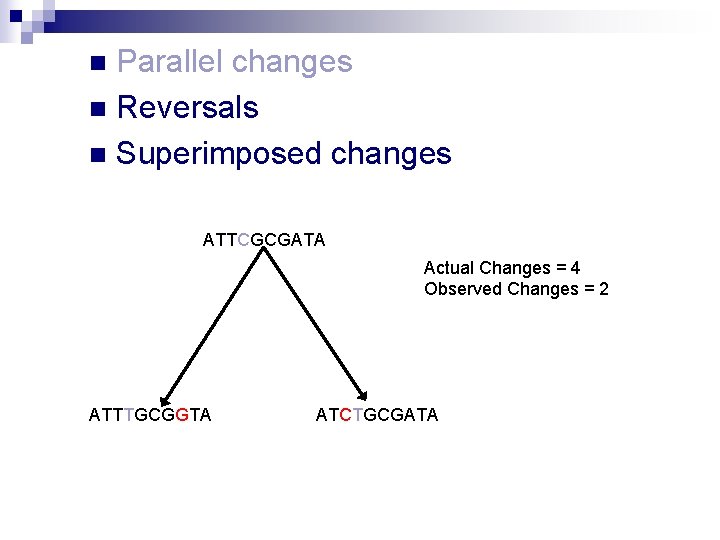
Parallel changes n Reversals n Superimposed changes n ATTCGCGATA Actual Changes = 4 Observed Changes = 2 ATTTGCGGTA ATCTGCGATA

Parallel changes n Reversals n Superimposed changes n ATTTGCGATA Actual Changes = 4 Observed Changes = 2 ATTCGCGATA ATTTGCGGTA ATCTGCGATA
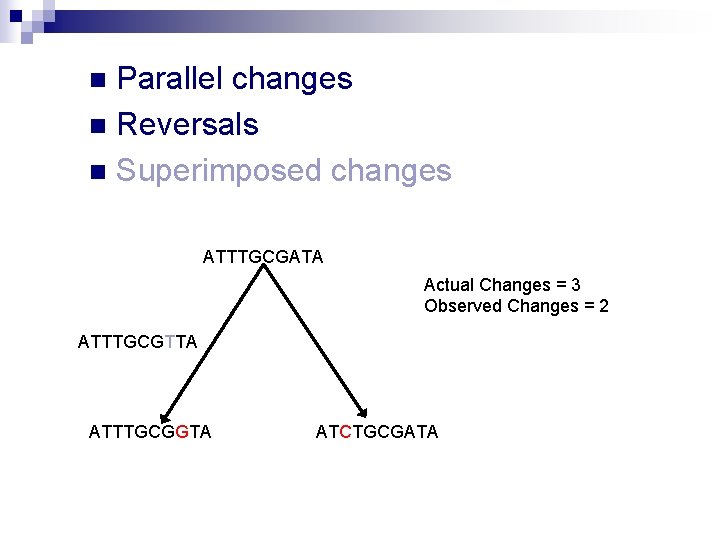
Parallel changes n Reversals n Superimposed changes n ATTTGCGATA Actual Changes = 3 Observed Changes = 2 ATTTGCGTTA ATTTGCGGTA ATCTGCGATA

Correcting for hidden changes n Given a statistical model of how point mutations occur it is possible to estimate the true genetic distance from the observed distance.

Correcting under a simple model n The Jukes-Cantor model states that all states {A, C, G, T} and all changes between states, e. g. A→C, are equally likely. A u/3 C u/3 G u/3 u/3 T As a mathematical conviencence imagine we have a rate 4 u/3 of change to a random state, this includes the possibility of a state changing to itself.

A Poisson process n The probability of no change at a site over time t is e-4/3 ut n The probability of at least one event is then 1 - e-4/3 ut n The probability of at least one event that leads to a different state from the one we started at is ¾(1 - e-4/3 ut) as one time out of four we will “mutate” to the same base we started with. n The expected observed distance d given a true genetic distance of ut is d = ¾(1 - e-4/3 ut) n Inverting this formula gives our correction D = ut = -3/4 ln (1 -4/3 d)

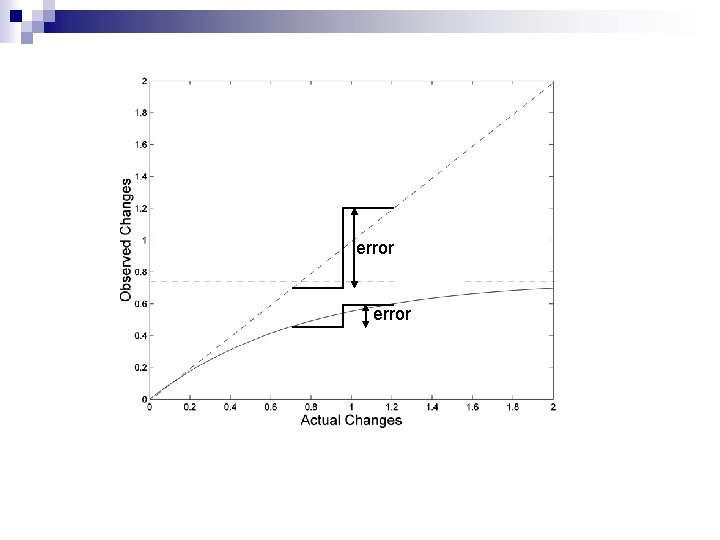
Correcting for hidden changes Correction for hidden changes has been shown (both theoretically and by simulation studies) to improve accuracy. n However, this is not universally true. n If data is clock-like then corrections will not change the relative size of the distances n However, the more complicated the model is the larger the variance (error) of the distances will become. n
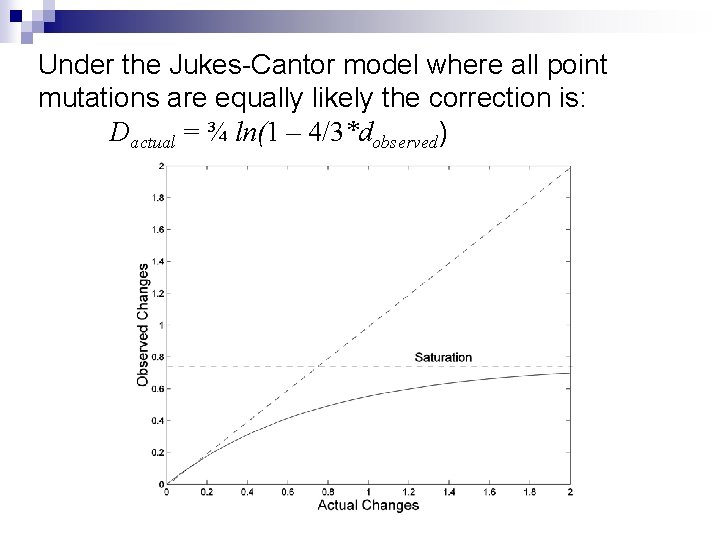
Under the Jukes-Cantor model where all point mutations are equally likely the correction is: Dactual = ¾ ln(1 – 4/3*dobserved)
error

An interesting observation n Uncorrected distances always obey the triangle inequality d(x, y) + d(y, z) >= d(x, z) But corrected distance do not. E. g. if sequences a and b differ at 10 / 100 sites and sequences b and c differ at a different 10 / 100 sites the uncorrected distances are d(a, b) = d(b, c) = 0. 1, d(a, c) = 0. 2 and the corrected distances (under the JC model) are D(a, b) = D(b, c) = 0. 107, D(a, c) = 0. 233

Tree building - UPGMA works by progressively clustering the most similar taxa until all the taxa form a rooted clock-like tree. 1. Find the smallest entry in the distance matrix, say d(x, y). 2. Form a new internal node, z, that is a parent to x and y and set the edge lengths from z to x and z to y to half d(x, y). 3. Update the distance matrix by setting the distances from the new node z to all the other taxa to be the average distance between groups x and y. REPEAT until all groups have been joined.

What precisely is meant by the average distance? n If we a joining two groups i and j that already have ni and nj members we update the distances using
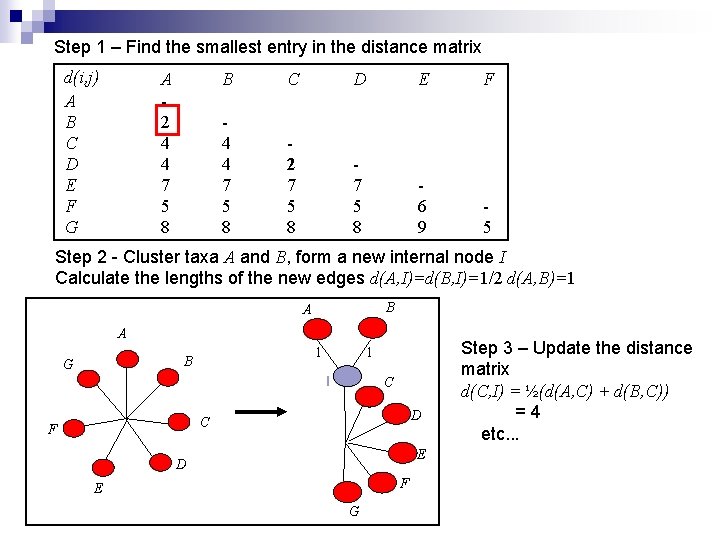
Step 1 – Find the smallest entry in the distance matrix d(i, j) A B C D E F G A 2 4 4 7 5 8 B C D E F 4 4 7 5 8 2 7 5 8 6 9 5 Step 2 - Cluster taxa A and B, form a new internal node I Calculate the lengths of the new edges d(A, I)=d(B, I)=1/2 d(A, B)=1 B A A 1 B G 1 I C D C F E D F E G Step 3 – Update the distance matrix d(C, I) = ½(d(A, C) + d(B, C)) =4 etc. . .
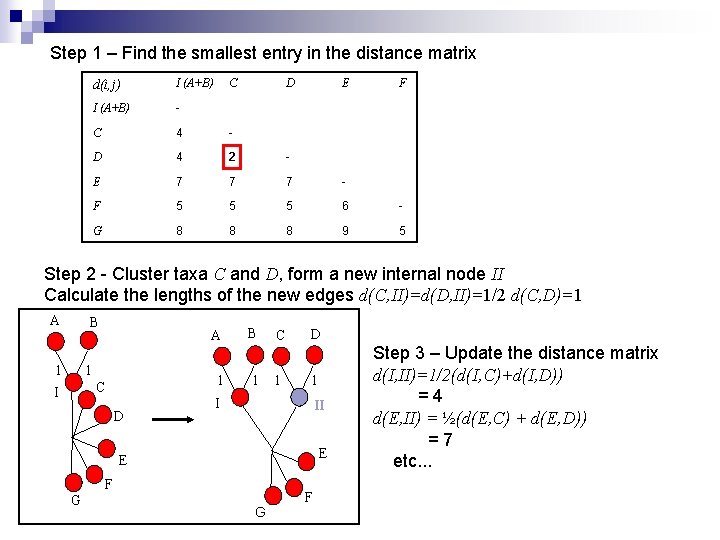
Step 1 – Find the smallest entry in the distance matrix d(i, j) I (A+B) - C 4 - D 4 2 - E 7 7 7 - F 5 5 5 6 - G 8 8 8 9 5 C D E F Step 2 - Cluster taxa C and D, form a new internal node II Calculate the lengths of the new edges d(C, II)=d(D, II)=1/2 d(C, D)=1 A B 1 A 1 1 C I D B 1 C 1 D 1 I II E E F G G F Step 3 – Update the distance matrix d(I, II)=1/2(d(I, C)+d(I, D)) =4 d(E, II) = ½(d(E, C) + d(E, D)) =7 etc. . .
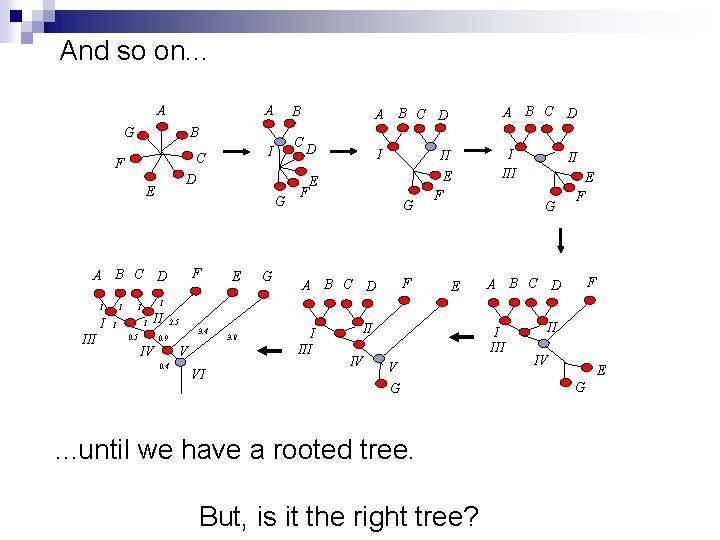
And so on. . . A G C III B C D I CD I II G F A B C D I A D E 1 B B F 1 A G E E G F A B C D I III F II E G E F F A B C D 1 1 E F A B C D II 0. 5 2. 5 3. 4 0. 9 IV V 0. 4 VI 3. 8 I II IV I III V G . . . until we have a rooted tree. But, is it the right tree? II IV E G

UPGMA is not consistent for additive distances d(i, j) A B C D E F G A 2 4 4 7 5 8 B C D E F 4 4 7 5 8 2 7 5 8 6 9 5 C A A 1 1 B D 1 1 = 4 1 1 F D E E 1 1 1 B C The tree that matches the distances is not recovered by UPGMA. 1 I 1 1 1 III 2. 5 1 3. 4 0. 5 IV 4 V 0. 4 F G 3. 8 0. 9 VI G

Inconsistency When a method is given “perfect” data but still gets the wrong tree it is said to be inconsistent. n UPGMA is inconsistent for data that isn’t ultrametric (clock-like). n Next we’ll look at a method that is consistent for any additive data. n

Neighbor-joining (NJ) NJ works by progressively clustering taxa until all the taxa form an unrooted tree. 1. Rather than using the distance matrix directly to determine which taxa should be clustered at each stage, NJ uses the S matrix where S(i, j) = (N-2)d(i, j) - R(i) - R(j) N is the number of taxa. R(i) is the sum of the ith row in the distance matrix. R(j) is the sum of the jth row in the distance matrix. 2. Find the smallest entry in the S matrix, say S(x, y).

Form a new internal node, z, that is a parent to x and y and calculate the edge lengths from z to x and z to y. d(x, z) = 1/(2(N-2))[(N-2)d(x, y) + R(x) – R(y)] d(y, z) = d(x, y) – d(x, z) 3. 4. Update the distance matrix d(w, z) = ½ (d(x, w) + d(y, w) – d(x, y)) REPEAT until only two things are left to be joined.

NJ Example D= Dog Cat Dog Rat Step 1 3 Rat 4 5 Cow 6 7 Cat S= Dog -22 Rat -20 Cow -20 6 R(cat) = 13 R(dog) = 15 R(rat) = 15 R(cow) = 19 e. g. S(cat, dog) = (4 -2)x 3 – 15 = -22 S(cat, rat) = (4 -2)x 4 – 13 – 15 = -20 Rat -22
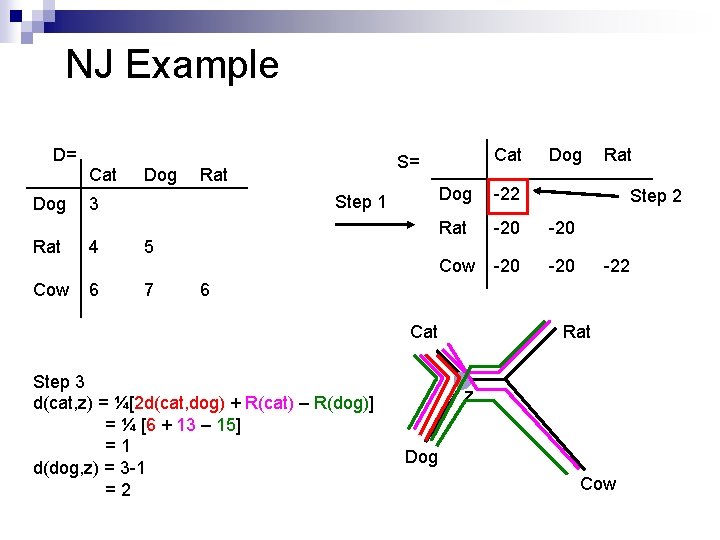
NJ Example D= Dog Cat Dog Rat Step 1 3 Rat 4 5 Cow 6 7 Cat S= Dog -22 Rat -20 Cow -20 Rat Step 2 -22 6 Cat Step 3 d(cat, z) = ¼[2 d(cat, dog) + R(cat) – R(dog)] = ¼ [6 + 13 – 15] =1 d(dog, z) = 3 -1 =2 Rat z Dog Cow
![Step 4 d(z, rat) = ½ [d(cat, rat) + d(dog, rat) – d(cat, dog)] Step 4 d(z, rat) = ½ [d(cat, rat) + d(dog, rat) – d(cat, dog)]](http://slidetodoc.com/presentation_image_h2/7423f8b55cf9f4d62633547c2e626845/image-40.jpg)
Step 4 d(z, rat) = ½ [d(cat, rat) + d(dog, rat) – d(cat, dog)] = ½ [4 + 5 – 3] =3 Cat d(z, cow) = ½ [6 + 7 – 3] =5 Rat z Dog Cow

Global vs Local methods n UPGMA and NJ are local construction methods. At each step they pick they best pair of taxa to cluster, once a decision is made it cannot be unmade. This makes these methods very fast. n There also global methods for making trees based on distances. These evaluate an optimality criterion on each possible tree and then pick the tree with the best score. Examples of global methods for distance data include least squares and minimum evolution. Because the number of trees grows very quickly with the number of taxa, these methods are slow.

Least Squares n We would like the path lengths on the tree we choose to be as close as possible to the corresponding values in the distance matrix. n With additive data we can always find a tree where the path length distances and the distance matrix match exactly. However, most data isn’t perfect. . . n We can try and minimise the discrepency between the observed distances and the tree distances using a least squares approach.

A family of least squares methods wij = 1 unweighted least squares (Cavalli-Sforza and Edwards 1967) wij =1/Dij wij = 1/Dij 2 (Fitch and Margoliash 1967)

Picking the best weights for a given tree The tree distances dij can be represented by the equation where xij, k is an indicator variable that is 1 if edge k lies on the path from i to j and 0 otherwise. We want to find edge weights ek that minimise
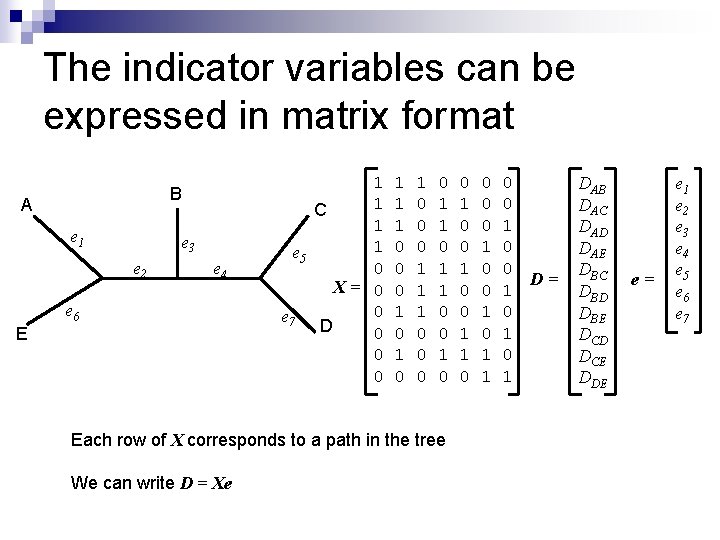
The indicator variables can be expressed in matrix format B A e 1 e 3 e 2 e 4 e 6 E 1 1 C 1 1 e 5 0 X= 0 0 e 7 D 0 0 0 1 1 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 0 Each row of X corresponds to a path in the tree We can write D = Xe 0 1 0 0 1 1 0 0 D= 1 0 1 DAB DAC DAD DAE DBC DBD DBE DCD DCE DDE e= e 1 e 2 e 3 e 4 e 5 e 6 e 7

Experience the joy of linear algebra D=Xe XTD = (XTX)e e = (XTX)-1 XTD This assumes that the weights wij = 1

Minimum evolution Uses the least squares method to fit the branch lengths for each tree n BUT uses a different optimality criterion than least squares. n Prefers the tree with the shortest sum of branch lengths n

Review n n n Observed distances derived from sequence alignments will always underestimate the true number of mutations. Hence it is ususally a good idea to correct for these hidden changes. Clustering methods like UPGMA and Neighborjoining are very fast as they only make local decisions and never backtrack. These methods are often used as a starting point for heuristic searches. There also optimality criteria that use distances as input, e. g. Least squares and minimum evolution.

Review n n n Not all distances can be fit perfectly onto a tree. Methods can be inconsistent, for example for some non-clocklike distances UPGMA is guaranteed to recover the wrong tree. UPGMA is consistent for clock-like distances and NJ is consistant for any additive distances.
- Slides: 49