Phylogenetics II Characterbased methods for constructing phylogenies In

Phylogenetics II

Character-based methods for constructing phylogenies In this approach, trees are constructed by comparing the characters of the corresponding species. Characters may be morphological (teeth structures) or molecular (nucleotides in homologous DNA sequences). One common approach is Maximum Parsimony Common Assumptions: • Independence of characters (no correlations) • Best tree is one where minimal changes take place

Character based methods: Input species C 1 C 2 C 3 C 4 … Cm dog A A C A G G T C T T C G A G G C C C horse A A C A G G C C T A T G A C C C frog A A C A G G T C T T T G A G T C C C human A A C A G G T C T T T G A C C pig A A C A G T T C G A T G G C C * * * • Each character (column) is processed independently. • The green character will separate the human and pig from frog, horse and dog. • The red character will separate the dog and pig from frog, horse and human. • We seek for a tree that will best explain all characters simultaneously.

1. Maximum Parsimony A Character-based method Input: • h sequences (one per species), all of length k. Goal: • Find a tree with the input sequences at its leaves, and an assignment of sequences to internal nodes, such that the total number of substitutions is minimized.

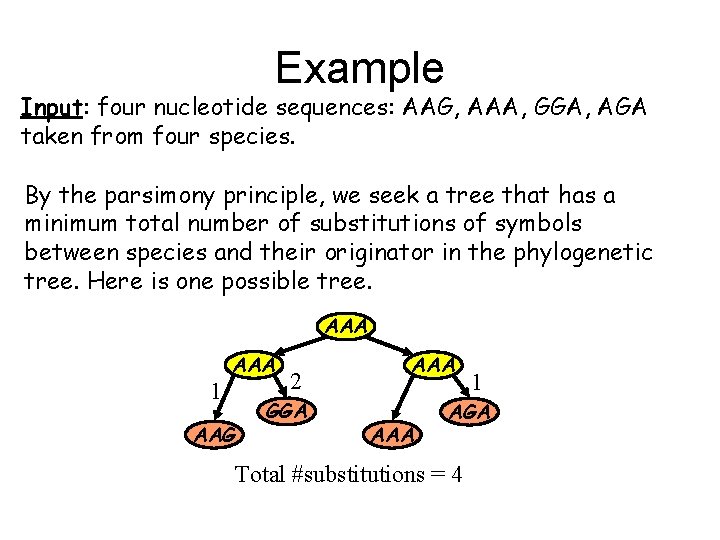
Example Input: four nucleotide sequences: AAG, AAA, GGA, AGA taken from four species. By the parsimony principle, we seek a tree that has a minimum total number of substitutions of symbols between species and their originator in the phylogenetic tree. Here is one possible tree. AAA 1 AAA AAG 2 GGA AAA 1 AGA Total #substitutions = 4

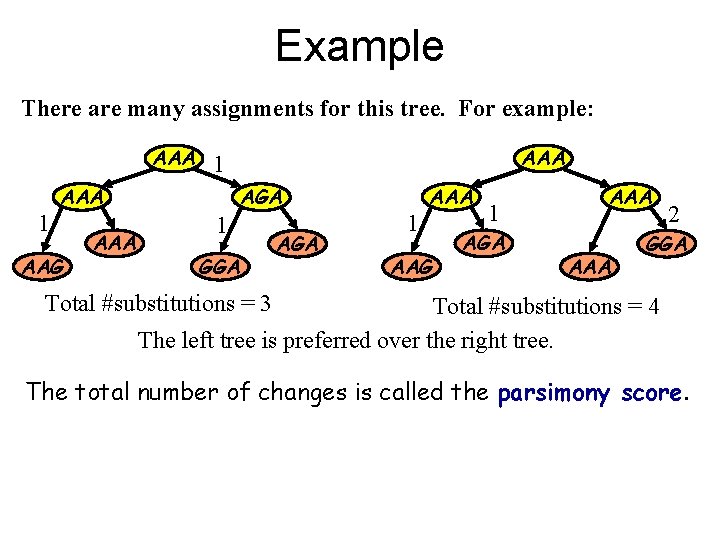
Example There are many assignments for this tree. For example: AAA 1 AAA AAG AAA 1 AGA 1 GGA AGA 1 AAA AAG 1 AGA AAA 2 GGA Total #substitutions = 3 Total #substitutions = 4 The left tree is preferred over the right tree. The total number of changes is called the parsimony score.

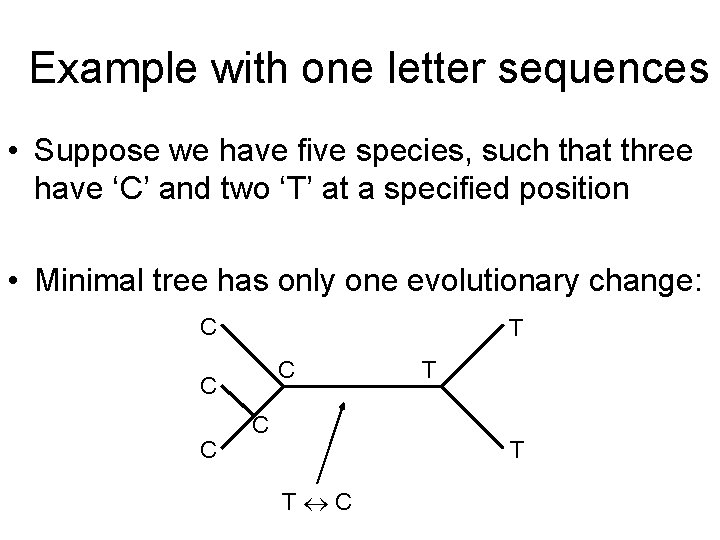
Example with one letter sequences • Suppose we have five species, such that three have ‘C’ and two ‘T’ at a specified position • Minimal tree has only one evolutionary change: C T C C T T T C

Parsimony Based Reconstruction Two separate components: 1. A procedure to find the minimum number of changes needed to explain the data for a given tree topology, where species are assigned to leaves. 2. A search through the space of trees. 3. We will see efficient algorithms for (1). (2) is hard.

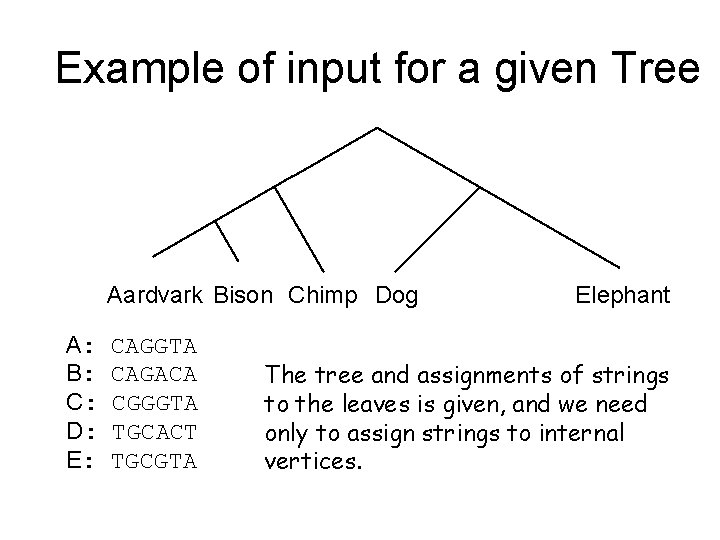
Example of input for a given Tree Aardvark Bison Chimp Dog A: B: C: D: E: CAGGTA CAGACA CGGGTA TGCACT TGCGTA Elephant The tree and assignments of strings to the leaves is given, and we need only to assign strings to internal vertices.

Fitch Algorithm Input: A rooted binary tree with characters at the leaves Output: Most parsimonious assignment of states to internal vertices Work on each position independently. Make one pass from the leaves to the root, and another pass from the root to the leaves. A A/T A A/C C T A

Fitch’s Algorithm traverse tree from leaves to root, fix a set of possible states (e. g. nucleotides) for each internal vertex traverse tree from root to leaves, pick a unique state for each internal vertex

Fitch’s Algorithm – Phase 1 Do a post-order (from leaves to root) traversal of tree, assign to each vertex a set of possible states. Each leaf has a unique possible state, given by the input. The possible states Ri of internal node i with children j and k is given by:

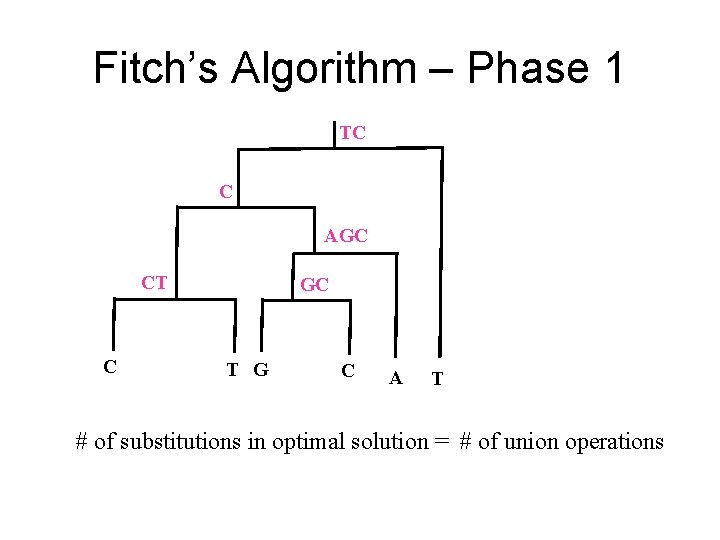
Fitch’s Algorithm – Phase 1 TC C AGC CT C GC T G C A T # of substitutions in optimal solution = # of union operations

Fitch’s Algorithm – Phase 2 do a pre-order (from root to leaves) traversal of tree select state rj of internal node j with parent i as follows:

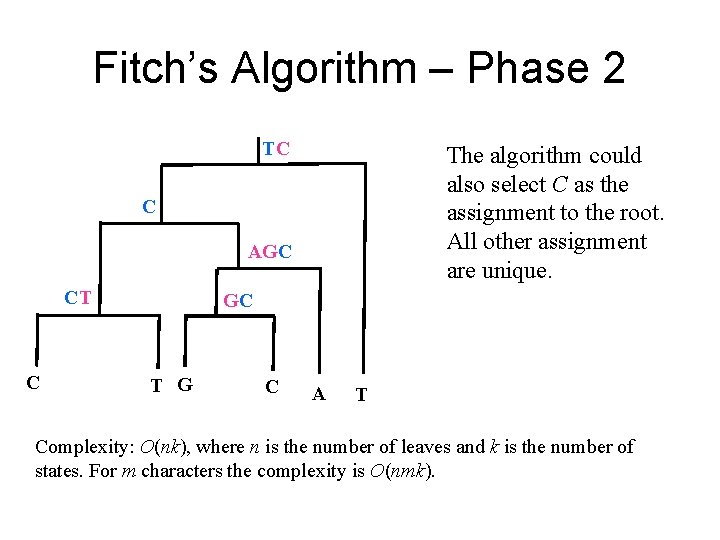
Fitch’s Algorithm – Phase 2 TC The algorithm could also select C as the assignment to the root. All other assignment are unique. C AGC CT C GC T G C A T Complexity: O(nk), where n is the number of leaves and k is the number of states. For m characters the complexity is O(nmk).

Generalization: Weighted Parsimony score: – Each change is weighted by a score c(a, b). – The weighted parsimony score reduces to the parsimony score when c(a, a)=0 and c(a, b)=1 for all b other than a.

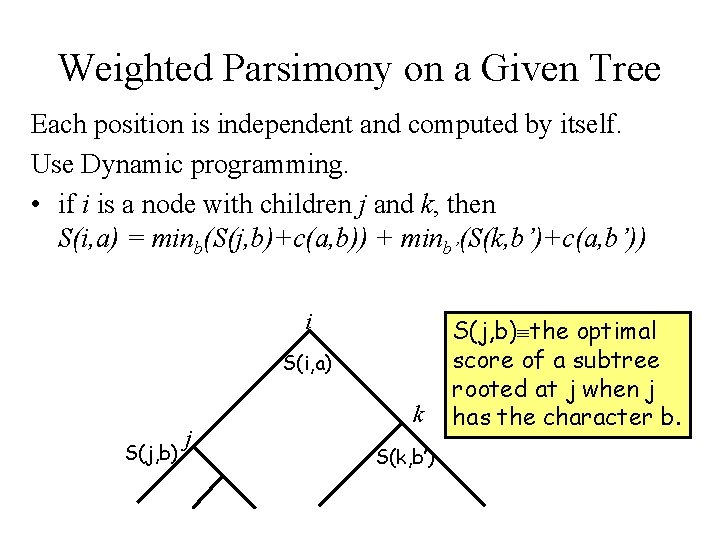
Weighted Parsimony on a Given Tree Each position is independent and computed by itself. Use Dynamic programming. • if i is a node with children j and k, then S(i, a) = minb(S(j, b)+c(a, b)) + minb’(S(k, b’)+c(a, b’)) i S(i, a) S(j, b) j k S(k, b’) S(j, b) the optimal score of a subtree rooted at j when j has the character b.

Evaluating Parsimony Scores (Sankoff’s algorithm) Dynamic programming on a given tree Initialization: • For each leaf i set S(i, a) = 0 if i is labeled by a, otherwise S(i, a) = Iteration: • if i is node with children j and k, then S(i, a) = minx(S(j, x)+c(a, x)) + miny(S(k, y)+c(a, y)) Termination: • cost of tree is minx. S(r, x) where r is the root

Cost of Evaluating Parsimony for binary trees For a tree with n nodes and a single character with k values, the complexity is O(nk 2). When there are m such characters, it is O(nmk 2).

2. Finding the right tree: The Perfect Phylogeny Problem The algorithms of Fitch and Sankoff assume that the tree is known. Finding the optimal tree is harder. Recall the general problem: Input: A set of species, specified by strings of characters. Output: A tree T, and assignment of species to the leaves of T, with minimum parsimony score.

The Perfect Phylogeny Problem Basic assumption for the perfect phylogeny problem: A character is a significant property, which distinguishes between species (e. g. dental structure). Hence, characters in evolutionary trees should be “Homoplasy free”, as we define next.

Homoplasy-free characters 1 Characters in Phylogenetic Trees should avoid: reversal transitions • A species regains a state it’s direct ancestor has lost. • Famous known reversals: – Teeth in birds. – Legs in snakes.

Homoplasy-free characters 2 …and also avoid convergence transitions • Two species possess the same state while their least common ancestor possesses a different state. • Famous known convergence: The marsupials.

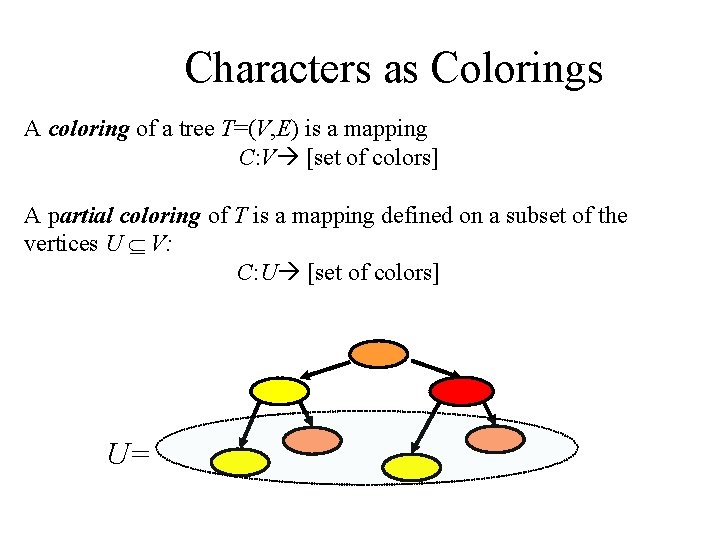
Characters as Colorings A coloring of a tree T=(V, E) is a mapping C: V [set of colors] A partial coloring of T is a mapping defined on a subset of the vertices U V: C: U [set of colors] U=

Characters as Colorings (2) Each character defines a (partial) coloring of the corresponding phylogenetic tree: Species ≡ Vertices States ≡ Colors

Convex Colorings (and Characters) Let T=(V, E) be a colored tree, and d be a color. The d-carrier is the minimal subtree of T containing all vertices colored d Definition: A (partial/total) coloring of a tree is convex iff all d-carriers are disjoint C

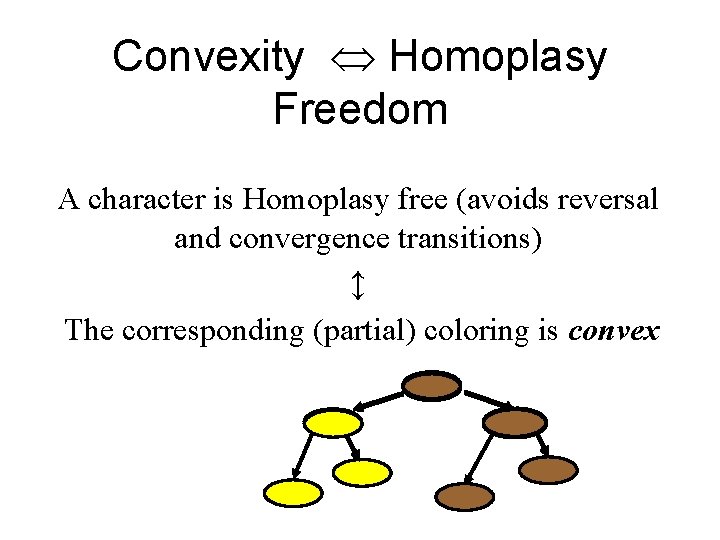
Convexity Homoplasy Freedom A character is Homoplasy free (avoids reversal and convergence transitions) ↕ The corresponding (partial) coloring is convex

The Perfect Phylogeny Problem • Input: a set of species, and many characters. • Question: is there a tree T containing the species as vertices, in which all the characters (colorings) are convex?

The Perfect Phylogeny Problem (pure graph theoretic setting) Input: Partial colorings (C 1, …, Ck) of a set of vertices U (in the example: 3 total colorings: left, center, right, each by two colors). RRB BBR RRR RBR Problem: Is there a tree T=(V, E), s. t. U V and for i=1, …, k, , Ci is a convex (partial) coloring of T? NP-Hard In general, in P for some special cases. Next we show a polynomial time algorithm for the case of binary characters.