Phylogenetic trees Level 3 Molecular Evolution and Bioinformatics

Phylogenetic trees Level 3 Molecular Evolution and Bioinformatics Jim Provan Page and Holmes: Chapter 2

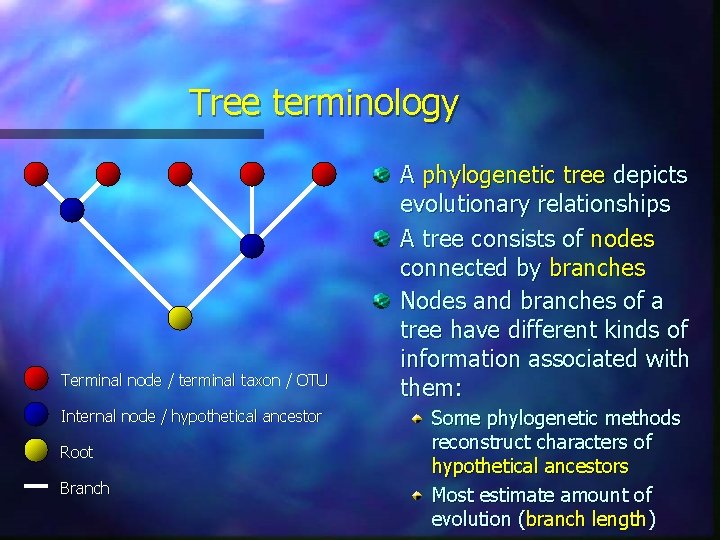
Tree terminology Terminal node / terminal taxon / OTU Internal node / hypothetical ancestor Root Branch A phylogenetic tree depicts evolutionary relationships A tree consists of nodes connected by branches Nodes and branches of a tree have different kinds of information associated with them: Some phylogenetic methods reconstruct characters of hypothetical ancestors Most estimate amount of evolution (branch length)

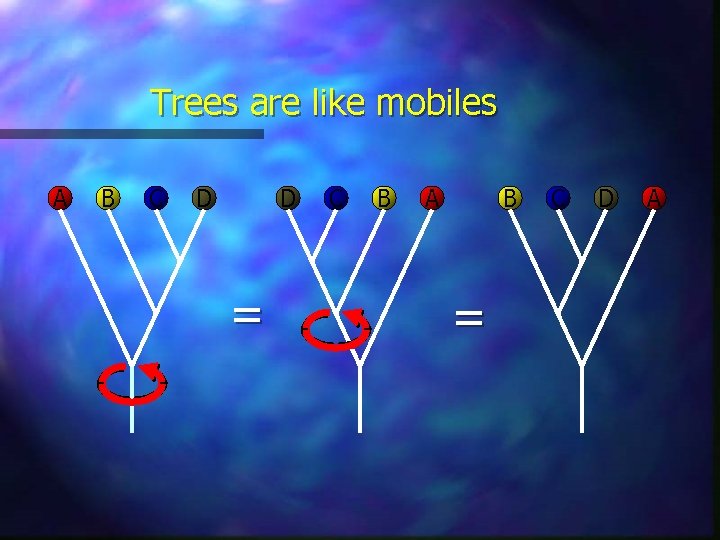
Trees are like mobiles A B C D D = C B A B = C D A

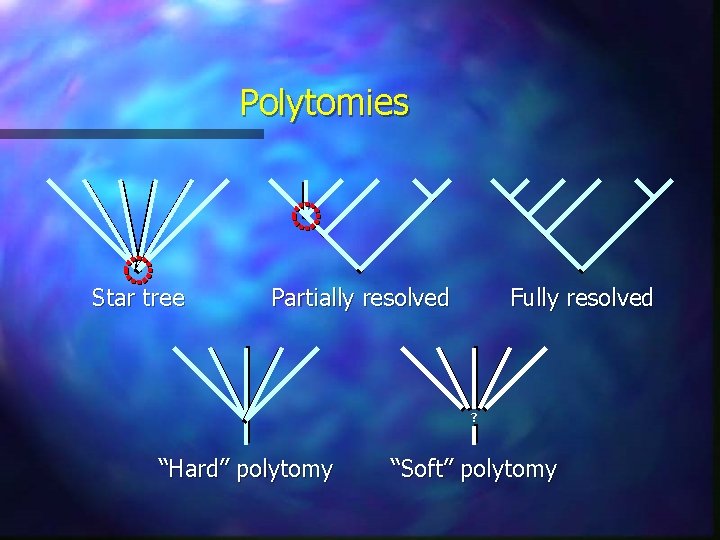
Polytomies Star tree Partially resolved Fully resolved ? “Hard” polytomy “Soft” polytomy

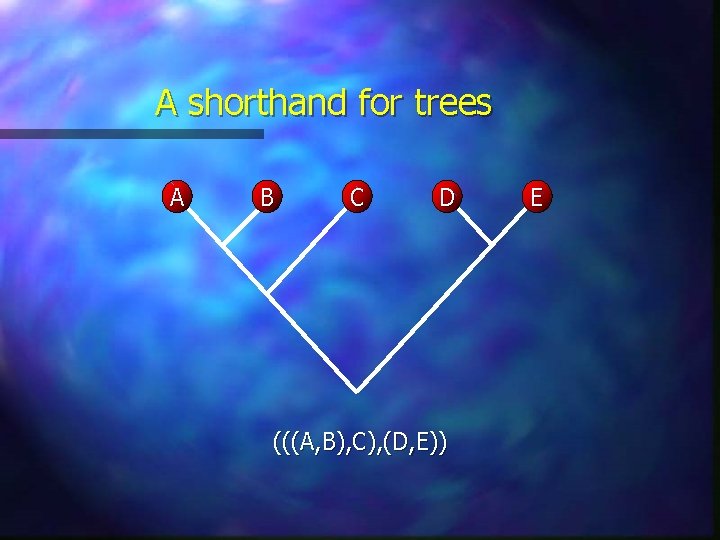
A shorthand for trees A B C D (((A, B), C), (D, E)) E

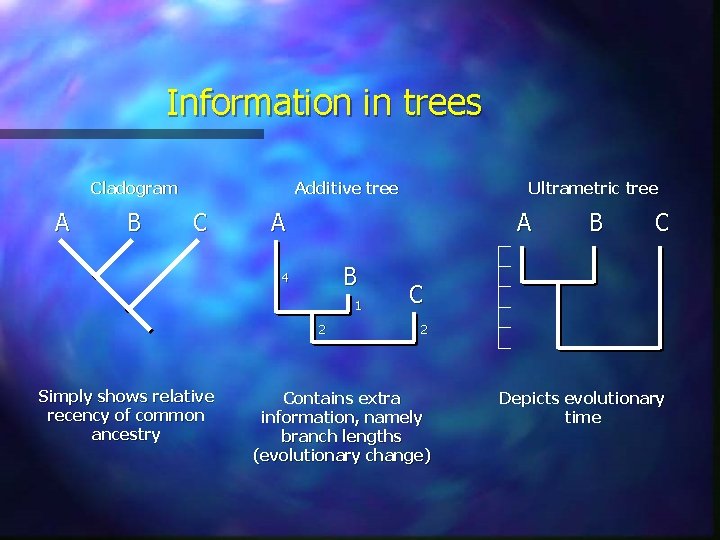
Information in trees Cladogram A B Additive tree C A A B 4 1 2 Simply shows relative recency of common ancestry Ultrametric tree B C C 2 Contains extra information, namely branch lengths (evolutionary change) Depicts evolutionary time

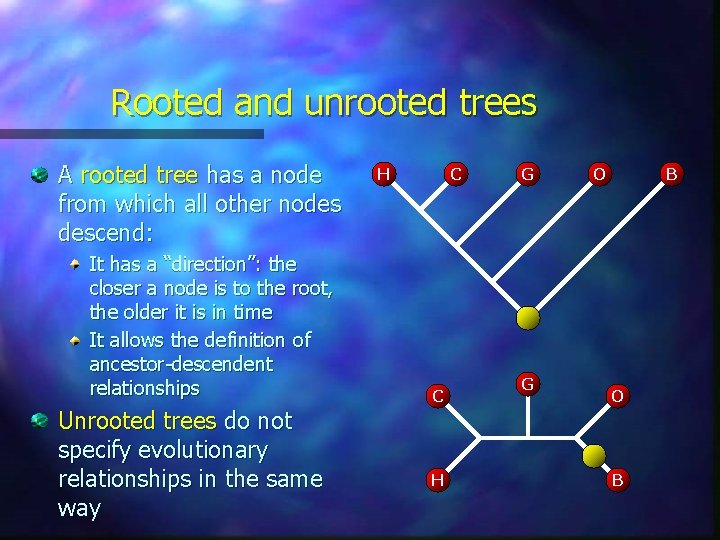
Rooted and unrooted trees A rooted tree has a node from which all other nodes descend: It has a “direction”: the closer a node is to the root, the older it is in time It allows the definition of ancestor-descendent relationships Unrooted trees do not specify evolutionary relationships in the same way H C C H G G O B

Numbers of rooted and unrooted trees The number of unrooted trees Un for n sequences is given by Un = (2 n – 5)(2 n – 7). . . (3)(1) The number of rooted trees Rn for n sequences is given by Rn = (2 n – 3)(2 n – 5). . . (3)(1) = (2 n – 3) Un n Un Rn 2 3 4 5 6 7 8 9 10 1 1 3 15 105 949 10 395 135 135 2 027 025 34 459 425 20 8 200 794 532 637 891 559 000

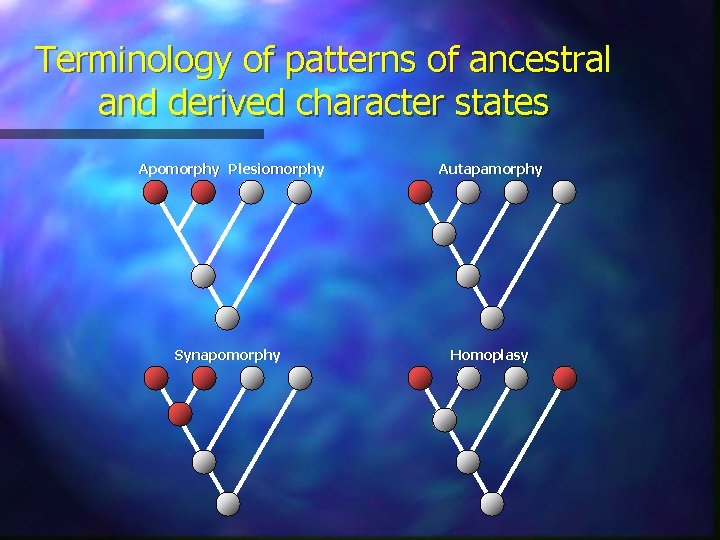
Terminology of patterns of ancestral and derived character states Apomorphy Plesiomorphy Autapamorphy Synapomorphy Homoplasy

Ancestors Phylogenies presuppose ancestors: Extinct organisms that left descendents which comprise modern species Represented by internal nodes of a tree Generally hypothetical and inferred from extant sequences Two recent developments have provided new problems in dealing with ancestors: Recovery of DNA from extinct taxa Viral sequences which evolve quickly enough to be tracked in “real time” Cladists have adopted the convention that extinct taxa lacking autapomorphies are ancestral

Metric distances In order for a distance measure to be used for building phylogenies, it must be a metric and it must be additive A distance d between two sequences, a and b, is a metric if it satisfies these properties: d(a, b) 0 d(a, b) = d(b, a) d(a, c) d(a, b) + d(b, c) d(a, b) = 0 if and only if a = b (non-negativity) (symmetry) (triangle inequality) (distinctness) In general, conditions 1, 2 and 4 are true for all measures of dissimilarity calculated directly from sequences

Ultrametric and additive distances A metric is an ultrametric if it satisfies the additional criterion that: d(a, b) maximum [d(a, c), d(b, c)] Ultrametric distances have the very useful evolutionary property of implying a constant rate of evolution: Idea of a molecular clock Relative rate test is a measure of how far pairwise differences between three sequences depart from ultrametricity To be additive, a measure must also satisfy the fourpoint condition: d(a, b) + d(c, d) maximum [d(a, c) + d(b, d), d(a, d) + d(b, c)] Of the three sums, the two largest must be equal

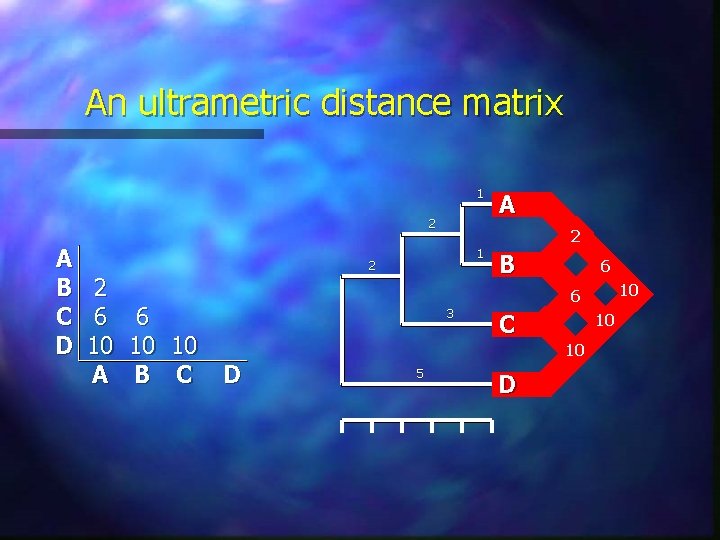
An ultrametric distance matrix 1 2 A B 2 C 6 6 D 10 10 10 A B C A 2 1 2 B 6 10 6 3 D C 10 10 5 D

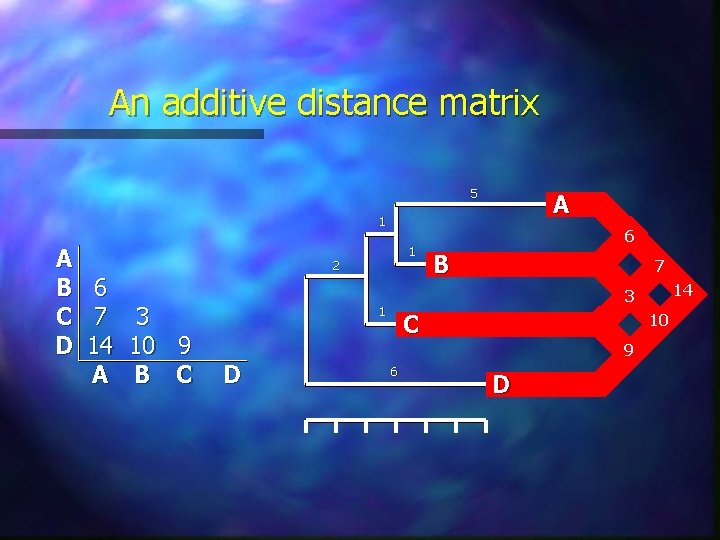
An additive distance matrix 5 A 1 A B 6 C 7 3 D 14 10 9 A B C 1 2 B 7 14 3 1 D 6 C 10 9 6 D

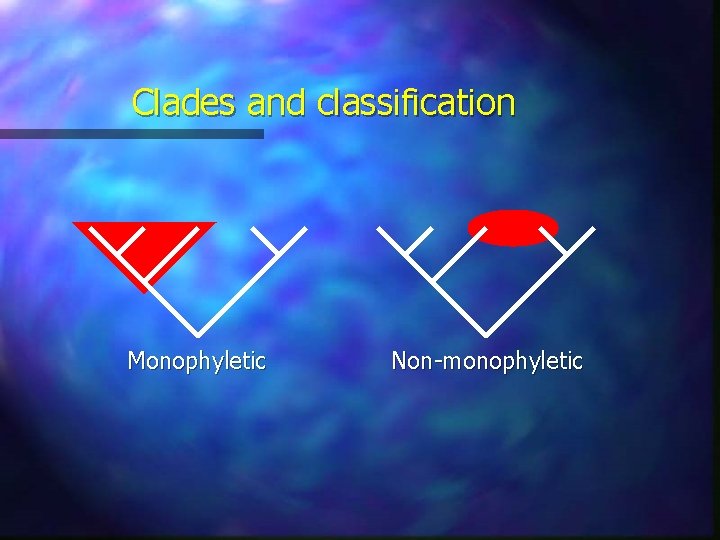
Clades and classification Monophyletic Non-monophyletic

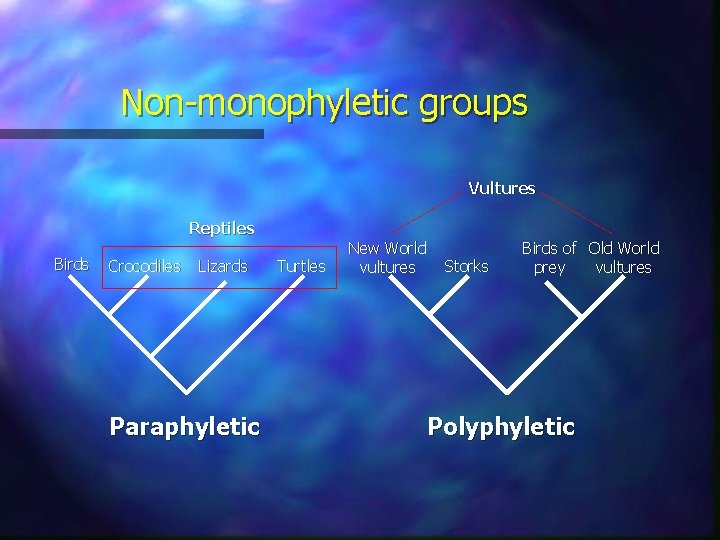
Non-monophyletic groups Vultures Reptiles Birds Crocodiles Lizards Paraphyletic Turtles New World vultures Storks Birds of Old World prey vultures Polyphyletic

Consensus trees H C G O H B C G H C O B G O B

Consensus trees A B C D E A B C D Strict A B C E A B C Majority-rule D E A B 67 100 67 C D E