PHY 151 Lecture 7 7 1 Nonisolated System

PHY 151: Lecture 7 7. 1 Nonisolated System (Energy) 7. 2 Isolated System (Energy) 7. 3 Nonisolated System in Steady State (Energy) 7. 4 Situations Involving Kinetic Friction 7. 5 Changes in Mechanical Energy for Nonconservative Forces • 7. 6 Power • 7. 7 Context Connection: Horsepower Ratings of Automobiles • • •

PHY 151: Lecture 7 Conservation of Energy 7. 1 Nonisolated System (Energy)

Nonisolated System (Energy) - 1 • In a nonisolated system: • Energy crosses boundary of the system due to interaction with the environment • For example, the work-kinetic energy theorem: • Interaction of system with environment is work done by external force • Quantity in system that changes is kinetic energy

Nonisolated System (Energy) - 2 Methods of energy transfer: • Work: transfers energy by applying a force and causing a displacement of the point of application of the force • Mechanical Waves: allow a disturbance to propagate through a medium • Heat: is driven by a temperature difference between two regions in space

Nonisolated System (Energy) - 3 • Matter Transfer: matter physically crosses the boundary of the system, carrying energy with it • Electrical Transmission: transfer is by electric current • Electromagnetic Radiation: energy is transferred by electromagnetic waves

Nonisolated System (Energy) - 4

Nonisolated System (Energy) - 5 • Energy is conserved • This means that energy cannot be created or destroyed • If the total amount of energy in a system changes, it can only be due to the fact that energy has crossed the boundary of the system by some method of energy transfer

Nonisolated System (Energy) - 6 • Mathematically, Esystem = ST • Esystem is the total energy of the system • T is the energy transferred across the system boundary • • • Note: Twork = W and Theat = Q Others do not have standard symbols, so we use: TMW (mechanical waves) TMT (matter transfer) TET (electrical transmission) TER (electromagnetic radiation)

Nonisolated System (Energy) - 7 • The primary mathematical representation of the energy analysis of a nonisolated system is • If all of the terms on the right are zero, the system is an isolated system • The Work-Kinetic Energy Theorem ( K = W) is a special case of the more general equation above

PHY 151: Lecture 7 Conservation of Energy 7. 2 Isolated System (Energy)

Isolated System (Energy) - 1 • Isolated system: no energy crosses the system boundary by any method • Example: lifting a book in a gravitational field • System consists of the book and the Earth • Mechanical energy: • System is isolated, so • Mechanical energy is conserved for isolated system with no nonconservative forces acting

Isolated System (Energy) - 2 • The changes in energy can be written out and rearranged • Kf + U f = K i + U i – Remember, this applies only to a system in which conservative forces act

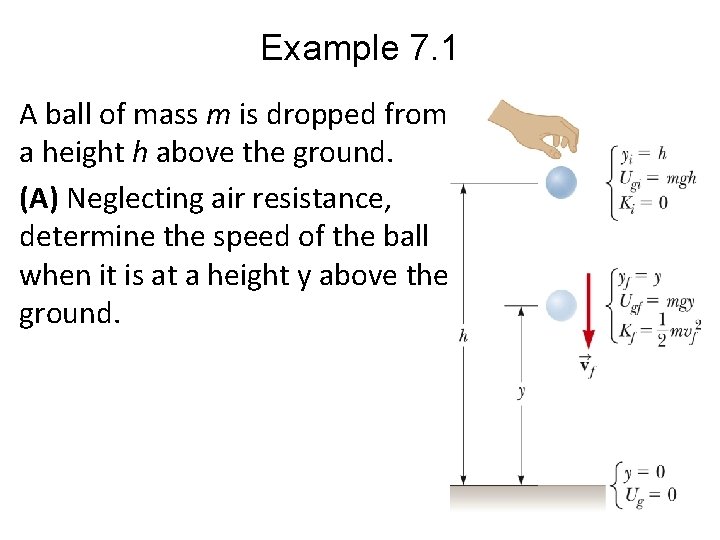
Example 7. 1 A ball of mass m is dropped from a height h above the ground. (A) Neglecting air resistance, determine the speed of the ball when it is at a height y above the ground.

Example 7. 1 • Apply the conservation of mechanical energy for the isolated system: • Solve for the final velocity:

Example 7. 1 (B) Determine the speed of the ball at y if at the instant of release it already has an initial upward speed vi at the initial altitude h. • Apply the conservation of mechanical energy for the isolated system: • Solve for the final velocity

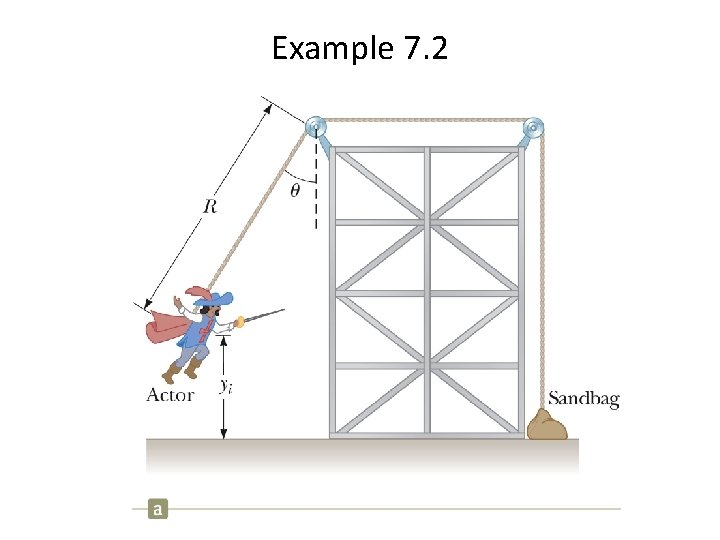
Example 7. 2 You are designing an apparatus to support an actor of mass 65 kg who is to “fly” down to the stage during the performance of a play. You attach the actor’s harness to a 130 -kg sandbag by means of a lightweight steel cable running smoothly over two frictionless pulleys. You need 3. 0 m of cable between the harness and the nearest pulley so that the pulley can be hidden behind a curtain.

Example 7. 2 For the apparatus to work successfully, the sandbag must never lift above the floor as the actor swings from above the stage to the floor. Let us call the initial angle that the actor’s cable makes with the vertical . What is the maximum value can have before the sandbag lifts off the floor?

Example 7. 2

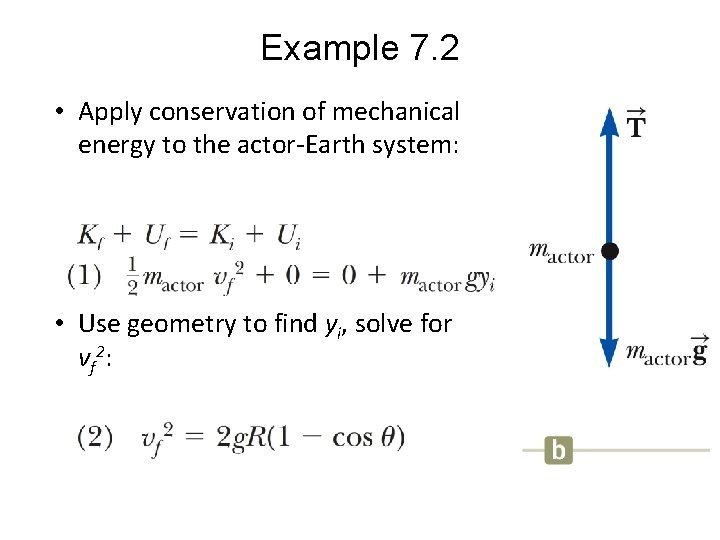
Example 7. 2 • Apply conservation of mechanical energy to the actor-Earth system: • Use geometry to find yi, solve for v f 2 :

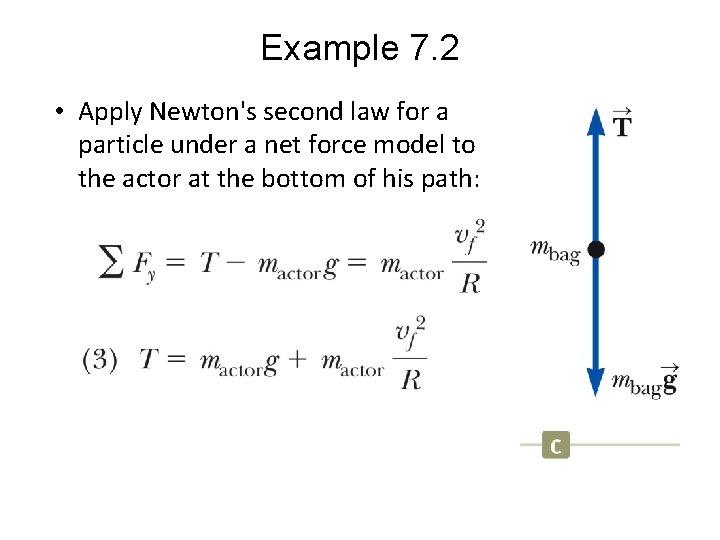
Example 7. 2 • Apply Newton's second law for a particle under a net force model to the actor at the bottom of his path:

Isolated System No Internal Friction - 1 K + U + Eint = W+Q + TMW + TMT + TER • For an isolated system, right side of the above equation = 0 because there are no energy transfers • For a system with no internal friction forces Eint = 0 • Emech = K + U = 0

Example 7. 2 • Substitute T = mbagg and Equation (2) into Equation (3): • Substitute values and solve for the angle:

Conservation of Mechanical Energy Example Aa • A person standing on a bridge at a height of 115 m above a river drops a 0. 250 -kg rock • (a) What is the rock’s mechanical energy at the time of release relative to the surface of the river? Ø Initially, at top of bridge, rock is not moving Ø Ki = 0 Ø Ei = Ki + Ui = 0 + mgh Ø Ei = 0. 250 x 9. 8 x 115 = 281. 75 joules

Conservation of Mechanical Energy Example Ab • A person standing on a bridge at a height of 115 m above a river drops a 0. 250 -kg rock • (b) What are rock’s kinetic, potential, and mechanical energies after it has fallen 75. 0 m? Ø After the rock falls 75. 0 m, its height is 40 m and the total mechanical energy is the same Ø E = 281. 75 J Ø U = mgh = 0. 25 x 9. 8 x 40 m = 98 J ØE = K + U Ø K = E – U = 281. 75 – 98 = 183. 75 J

Conservation of Mechanical Energy Example Ac • A person standing on a bridge at a height of 115 m above a river drops a 0. 250 -kg rock • (c) Just before the rock hits the water, what are its speed and total mechanical energy? Ø At bottom of fall, total mechanical energy, E, is 115 J Ø Potential energy is zero, because the height is now zero ØE = K + U Ø 281. 75 = K + 0 Ø K = 281. 75 = ½ mv 2 Ø v =sqrt(281. 75 x 2 /0. 25) = 47. 5 m/s

Conservation of Mechanical Energy Example B • A 60 -kg stunt person runs off a cliff at 5. 0 m/s and lands safely in the river 10. 0 m below. What was his speed when he landed? Ø Mechanical energy is conserved in this problem Ø Ef =Ei Ø mghf + ½ mvf 2 = mghi + ½ mvi 2 Ø Mass, m, cancels out of this problem Ø hi = 10. 0 m Ø hf = 0 m Ø vi = 5. 0 m/s Ø (9. 8)(0) + ½ vf 2 = (9. 8)(10. 0) + ½ (9. 8)(5)2 Ø vf = sqrt[2(98 + 122. 5)] = 29. 7 m/s

Conservation of Mechanical Energy Example C • • • A skier coasts down a very smooth, 10 -m-high slope The speed of the skier on the top of the slope is 5. 0 m/s What is his speed at the bottom of the slope? Mechanical energy is conserved because there is no friction Ef = E i ½ mvf 2 + mghf = ½ mvi 2 + mgh At the bottom of the hill hf = 0 Mass, m, cancels out of the problem ½ vf 2 + 0 = ½ vi 2 + ghi vf 2 = vi 2 + 2 ghi vf = sqrt(vi 2 + 2 ghi) = sqrt(5. 02 + 2(9. 8)10) = 14. 8 m/s

Conservation of Mechanical Energy - Ex D • A 14. 2 x 103 N auto is traveling at 26. 7 m/s • Auto runs out of gas 16 x 103 m from a service station • Neglecting friction, if station is on a level 15. 2 m above elevation where car stalled, how fast will the car be going when it rolls into the station, if in fact it gets there? Ø Ø Ø Ø Ø There is no friction. Mechanical energy is conserved. Ef = E i ½ mvf 2 + mghf = ½ mvi 2 + mghi The initial height is taken as zero ½ mvf 2 + mghf = ½ mvi 2 + 0 ½ vf 2 + ghf = ½ vi 2 vf 2 + 2 ghf = vi 2 vf = sqrt(vi 2 – 2 ghf) = sqrt(26. 72 – 2(9. 8)(15. 2)) vf = sqrt(414. 97) = 20. 37 m/s

Example 7. 3 The launching mechanism of a popgun consists of a trigger-released spring. The spring is compressed to a position y. A and the trigger is fired. The projectile of mass m rises to a position y. C above the position at which it leaves the spring. Consider a firing of the gun for which m = 35. 0 g, y. A = 0. 120 m, and y. C = 20. 0 m.

Example 7. 3 (A) Neglecting all resistive forces, determine the spring constant. • Write a conservation of mechanical energy equation for the system between points A and C: • Substitute for each energy:

Example 7. 3 • Solve for k: • Substitute numerical values:

Example 7. 3 (B) Find the speed of the projectile as it moves through the equilibrium position B of the spring • Write a conservation of mechanical energy equation for the system between points A and B: • Substitute for each energy:

Example 7. 3 • Solve for the velocity: • Substitute numerical values:

PHY 151: Lecture 7 Conservation of Energy 7. 3 Nonisolated System in Steady State (Energy)

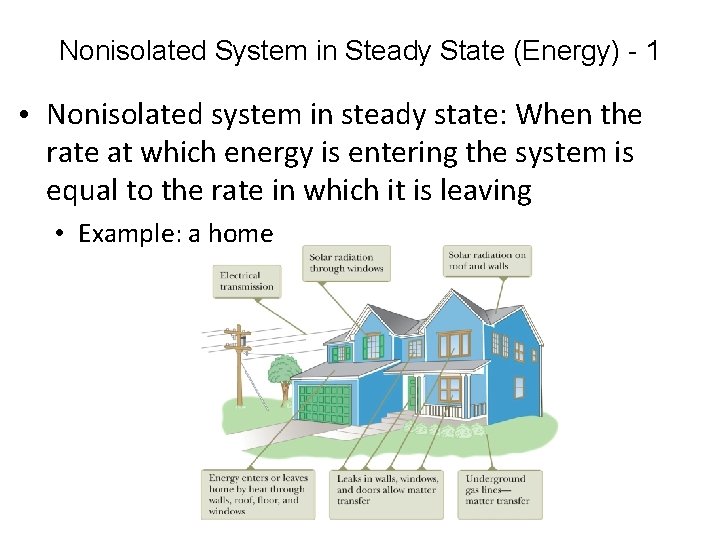
Nonisolated System in Steady State (Energy) - 1 • Nonisolated system in steady state: When the rate at which energy is entering the system is equal to the rate in which it is leaving • Example: a home

Nonisolated System in Steady State (Energy) – 2 • Example: the Earth-atmosphere system • Energy is transferred through electromagnetic radiation • Primary input radiation is from the Sun • Primary output radiation is infrared radiation emitted from atmosphere and ground • Ideally, transfers are balanced so Earth maintains a constant temperature • In reality, transfers are not exactly balanced • Earth is in quasi-steady state

PHY 151: Lecture 7 Conservation of Energy 7. 4 Situations Involving Kinetic Friction

Situations Involving Kinetic Friction - 1 • When kinetic friction is involved in a problem, you must use a modification of the work-kinetic energy theorem • Consider a book sliding on a table • The change in kinetic energy is equal to the work done by all forces other than friction minus the energy associated with the friction force:

Situations Involving Kinetic Friction - 2 • A friction force transformed kinetic energy in a system to internal energy • The increase in internal energy of the system is equal to its decrease in kinetic energy:

Example 7. 4 A 6. 0 -kg block initially at rest is pulled to the right along a horizontal surface by a constant horizontal force of 12 N. (A) Find the speed of the block after it has moved 3. 0 m if the surfaces in contact have a coefficient of kinetic friction of 0. 15.

Example 7. 4 • Find the work done on the system by the applied force: • Apply the particle in equilibrium model to the block in the vertical direction: • Find the magnitude of the friction force:

Example 7. 4 • Find the speed of the block: • Substitute numerical values:

Example 7. 4 (B) Suppose the force is applied at an angle. At what angle should the force be applied to achieve the largest possible speed after the block has moved 3. 0 m to the right?

Example 7. 4 • Find the work done by the applied force: • Apply the particle in equilibrium model to the block in the vertical direction: • Solve for n:

Example 7. 4 • Find the final kinetic energy: • Differentiate Kf with respect to and set the result equal to zero: • Evaluate for = 0. 15:

Example 7. 5 A block of mass 1. 6 kg is attached to a horizontal spring that has a force constant of 1000 N/m. The spring is compressed 2. 0 cm and is then released from rest. (A) Calculate the speed of the block as it passes through the equilibrium position x = 0 if the surface is frictionless.

Example 7. 5 • Find the work done by the spring on the system: • Use the work energy theorem to find the speed: • Substitute numerical values:

Example 7. 5 (B) Calculate the speed of the block as it passes through the equilibrium position if a constant friction force of 4. 0 N retards its motion from the moment it is released. • Write the equation for the final kinetic energy: • Substitute numerical values:

PHY 151: Lecture 7 Conservation of Energy 7. 5 Changes in Mechanical Energy for Nonconservative Forces

Changes in Mechanical Energy for Nonconservative Forces - 1 • In general, if friction is acting within an isolated system: • U is the change in all forms of potential energy • If the system in which nonconservative forces act is nonisolated and the external influence on the system is by means of work, we have

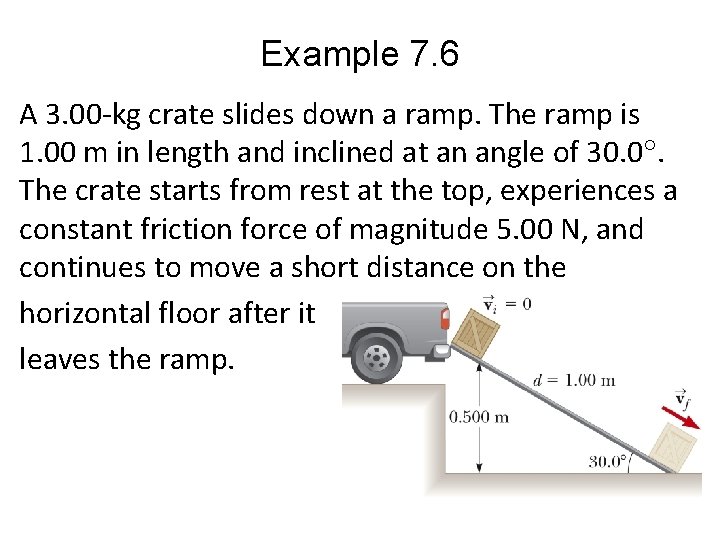
Example 7. 6 A 3. 00 -kg crate slides down a ramp. The ramp is 1. 00 m in length and inclined at an angle of 30. 0. The crate starts from rest at the top, experiences a constant friction force of magnitude 5. 00 N, and continues to move a short distance on the horizontal floor after it leaves the ramp.

Example 7. 6 (A) Use energy methods to determine the speed of the crate at the bottom of the ramp. • Write the expression for the total mechanical energy of the system when the crate is at the top: • Write an expression for the final mechanical energy: • Find Emech:

Example 7. 6 • Solve for the final velocity: • Substitute numerical values:

Example 7. 6 (B) How far does the crate slide on the horizontal floor if it continues to experience a friction force of magnitude 5. 00 N? • Write an expression for the mechanical energy of the system when the crate leaves the bottom of the ramp:

Example 7. 6 • Apply the expression for the change in mechanical energy with Ef = 0: • Solve for d and substitute numerical values:

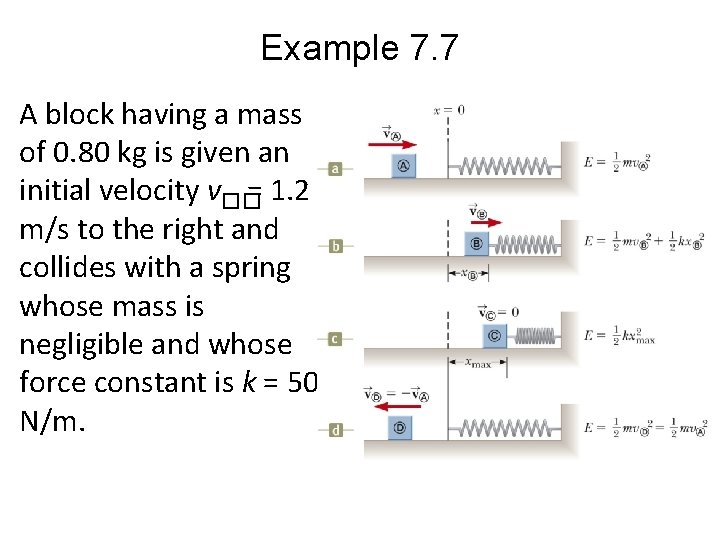
Example 7. 7 A block having a mass of 0. 80 kg is given an initial velocity v�� = 1. 2 m/s to the right and collides with a spring whose mass is negligible and whose force constant is k = 50 N/m.

Example 7. 7 (A) Assuming the surface to be frictionless, calculate the maximum compression of the spring after the collision. – Write a conservation of mechanical energy equation: – Solve for xmax and evaluate:

Example 7. 7 (B) Suppose a constant force of kinetic friction acts between the block and the surface, with k = 0. 50. If the speed of the block at the moment it collides with the spring is v. A = 1. 2 m/s, what is the maximum compression x. C in the spring? • Evaluate the magnitude of the friction force:

Example 7. 7 • Write the change in the mechanical energy of the system due to friction as the block is displaced from x = 0 to x. C: • Substitute the initial and final energies: • Substitute numerical values:

Example 7. 8 Two blocks are connected by a light string that passes over a frictionless pulley. The block of mass m 1 lies on a horizontal surface and is connected to a spring of force constant k. The system is released from rest when the spring is unstretched. If the hanging block of mass m 2 falls a distance h before coming to rest, calculate the coefficient of kinetic friction between the block of mass m 1 and the surface.

Example 7. 8 • Note that the system is isolated, so set the change in energies equal to zero: • There are two types of potential energies and K = 0: • Find the change in internal energy due to friction: • Evaluate the change in gravitational potential energy of the system:

Example 7. 8 • Evaluate the change in the elastic potential energy of the system: • Substitute Equations (2), (3), and (4) into Equation (1): • Solve for k:

PHY 151: Lecture 7 Conservation of Energy 7. 6 Power

Power - 1 • The time rate of energy transfer is called the instantaneous power: • The average power is • The instantaneous power is the limiting value of the average power as t approaches zero:

Power - 2 • The SI unit of power: 1 W = 1 J/s = 1 kg·m 2/s 3 • The U. S. customary system units of power: – Horsepower: 1 hp = 746 W – Kilowatt-hour: 1 k. Wh = (103 W)(3 600 s) = 3. 60× 106 J

Example 7. 9 An elevator car has a mass of 1600 kg and is carrying passengers having a combined mass of 200 kg. A constant friction force of 4000 N retards its motion.

Example 7. 9 (A) How much power must a motor deliver to lift the elevator car and its passengers at a constant speed of 3. 00 m/s? • Use the particle in equilibrium model for the car: • Solve for T:

Example 7. 9 • Use the equation for power: • Substitute numerical values:

Example 7. 9 (B) What power must the motor deliver at the instant the speed of the elevator is v if the motor is designed to provide the elevator car with an upward acceleration of 1. 00 m/s 2? • Use the particle under a net force model for the car: • Solve for T:

Example 7. 9 • Find the power: • Substitute numerical values:

PHY 151: Lecture 7 Conservation of Energy 7. 7 Context Connection: Hprsepower Ratings of Automobiles Skipped