PHY 1039 Properties of Matter Macroscopic Bulk Properties

PHY 1039 Properties of Matter Macroscopic (Bulk) Properties: Thermal Expansivity, Elasticity and Viscosity 20 & 23 February, 2012 Lectures 5 and 6

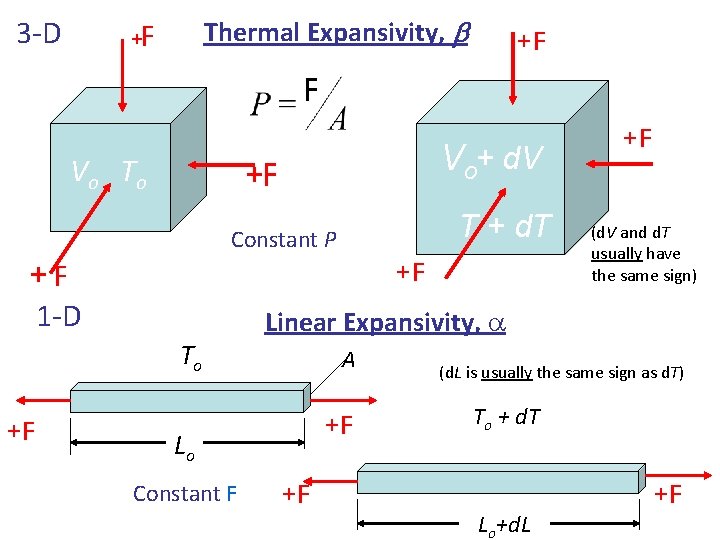
3 -D + Thermal Expansivity, b F +F F Vo To + d. T Vo+ d. V +F T + d. T Constant P +F +F 1 -D To +F (d. V and d. T usually have the same sign) Linear Expansivity, a A +F Lo Constant F +F +F (d. L is usually the same sign as d. T) To + d. T Lo+d. L +F

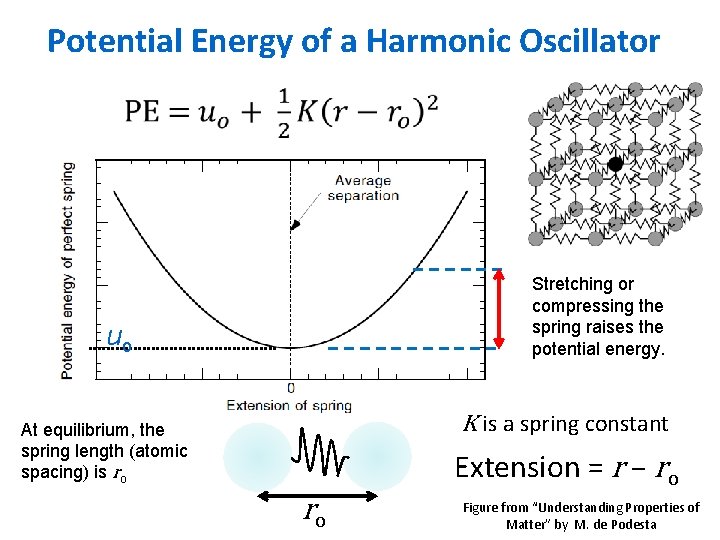
Potential Energy of a Harmonic Oscillator Stretching or compressing the spring raises the potential energy. uo K is a spring constant At equilibrium, the spring length (atomic spacing) is ro Extension = r – ro ro Figure from “Understanding Properties of Matter” by M. de Podesta

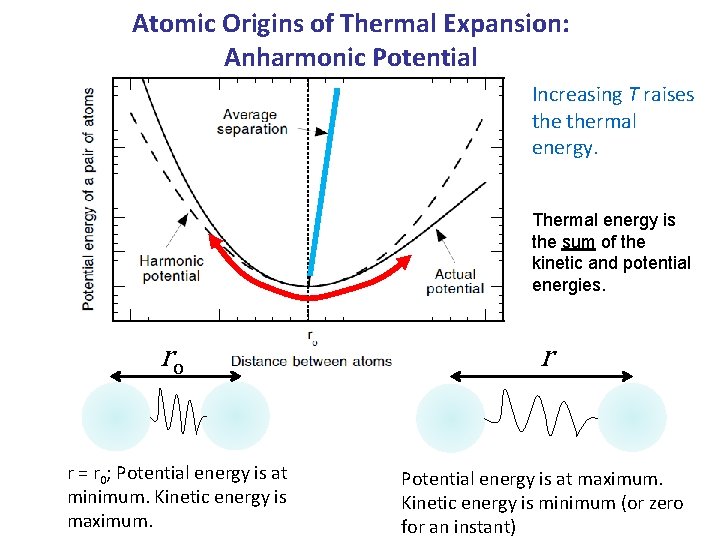
Atomic Origins of Thermal Expansion: Anharmonic Potential Increasing T raises thermal energy. Thermal energy is the sum of the kinetic and potential energies. ro r r = r 0; Potential energy is at minimum. Kinetic energy is maximum. Potential energy is at maximum. Kinetic energy is minimum (or zero for an instant)

Thermal Expansivity of Metals and Ceramics Substance (DL/L)*100% Steel Si. C T a increases slightly with temperature. Invar steel Pyrex glass Steel Aluminium Ice Water* Mercury* Linear expansivity, a (K-1) (room T) 1 x 10 -6 3 x 10 -6 11 x 10 -6 24 x 10 -6 51 x 10 -6 6 x 10 -4 * Deduced from b (b 3 a) bliquid >> bsolid

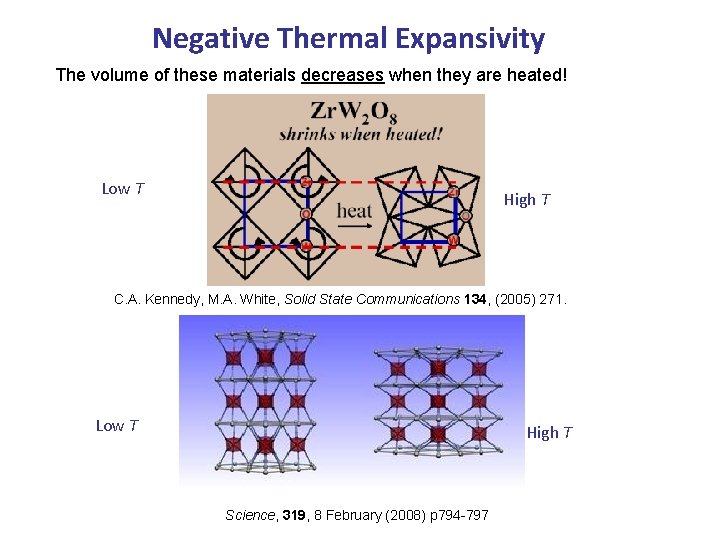
Negative Thermal Expansivity The volume of these materials decreases when they are heated! Low T High T C. A. Kennedy, M. A. White, Solid State Communications 134, (2005) 271. Low T High T Science, 319, 8 February (2008) p 794 -797

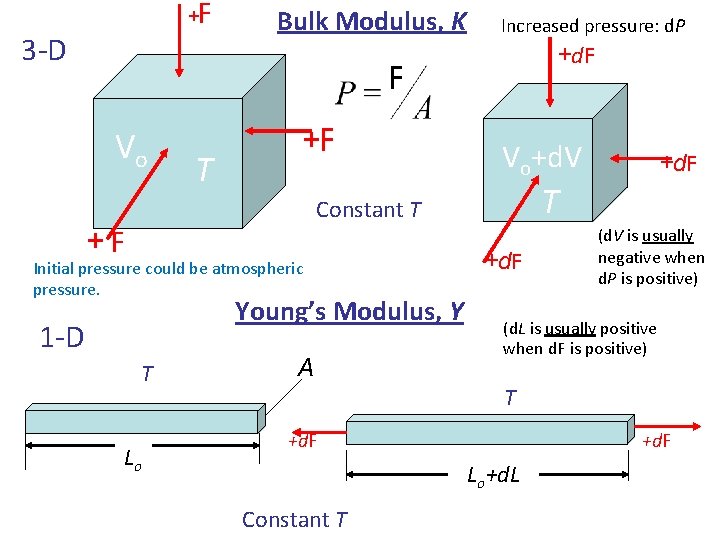
+ 3 -D F Bulk Modulus, K Increased pressure: d. P +d. F F Vo T +F Vo+d. V T Constant T +F Initial pressure could be atmospheric pressure. Young’s Modulus, Y 1 -D T Lo A +d. F (d. V is usually negative when d. P is positive) (d. L is usually positive when d. F is positive) T +d. F Lo+d. L Constant T +d. F

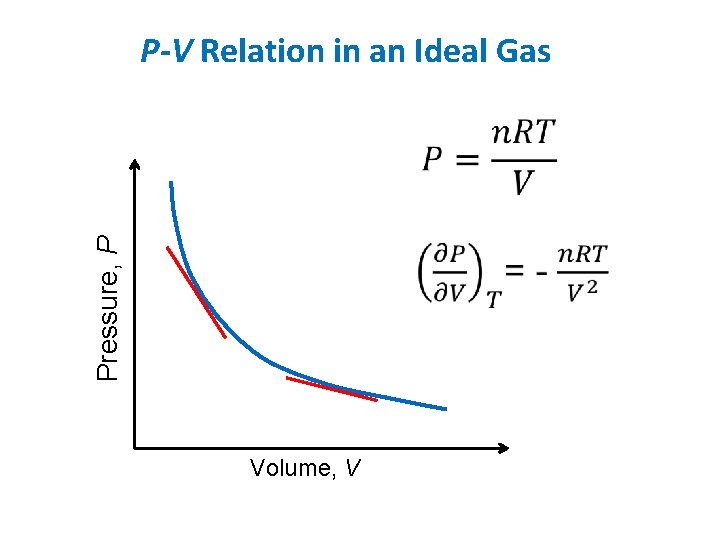
Pressure, P P-V Relation in an Ideal Gas Volume, V

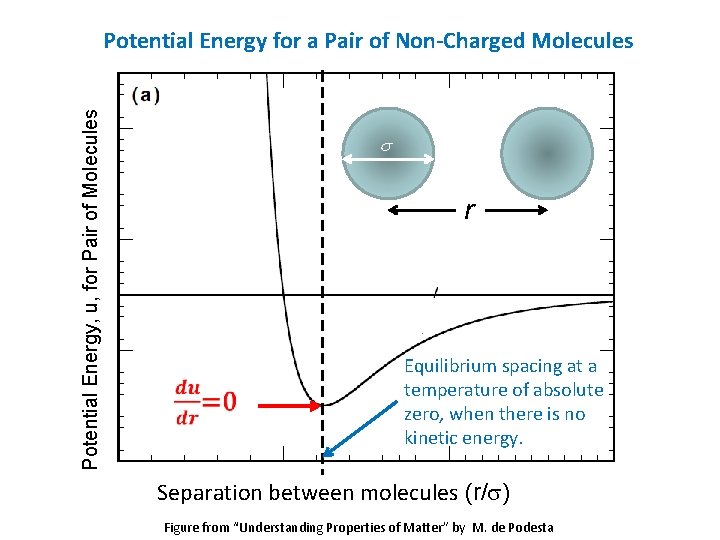
Potential Energy, u, for Pair of Molecules Potential Energy for a Pair of Non-Charged Molecules s r Equilibrium spacing at a temperature of absolute zero, when there is no kinetic energy. Separation between molecules (r/s) Figure from “Understanding Properties of Matter” by M. de Podesta

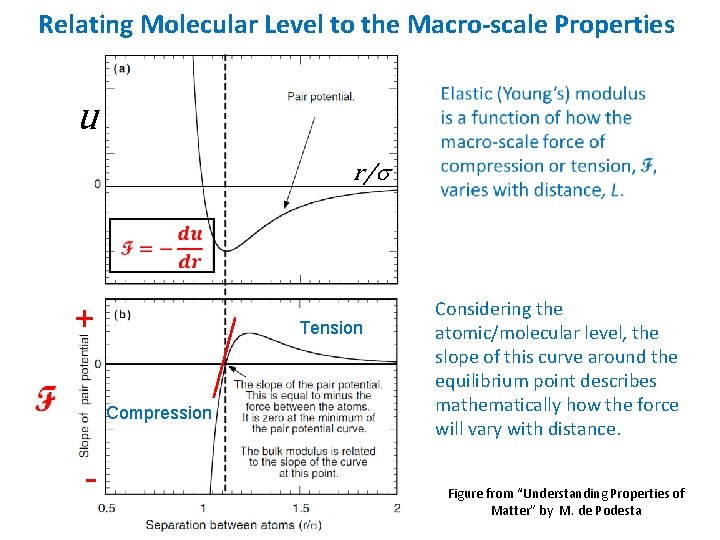
Relating Molecular Level to the Macro-scale Properties u r/s + Tension Compression - Considering the atomic/molecular level, the slope of this curve around the equilibrium point describes mathematically how the force will vary with distance. Figure from “Understanding Properties of Matter” by M. de Podesta

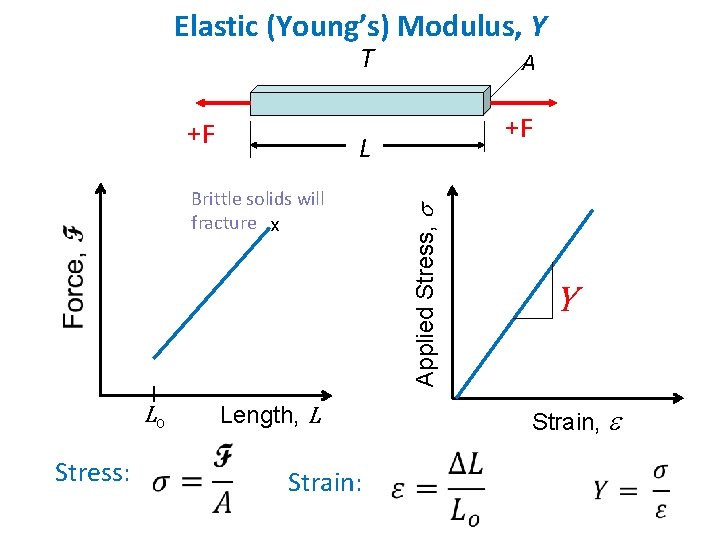
Elastic (Young’s) Modulus, Y T +F Stress: +F Length, L Strain: Applied Stress, s L Brittle solids will fracture x Lo A Y Strain, e

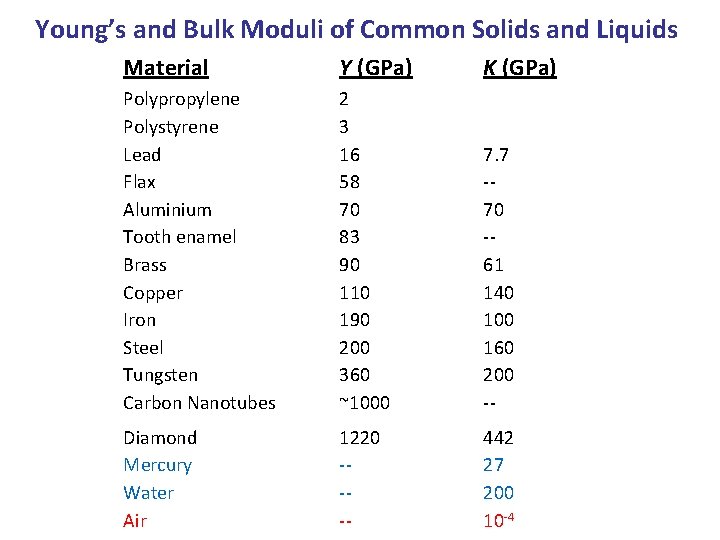
Young’s and Bulk Moduli of Common Solids and Liquids Material Y (GPa) K (GPa) Polypropylene Polystyrene Lead Flax Aluminium Tooth enamel Brass Copper Iron Steel Tungsten Carbon Nanotubes 2 3 16 58 70 83 90 110 190 200 360 ~1000 7. 7 -70 -61 140 100 160 200 -- Diamond Mercury Water Air 1220 ---- 442 27 200 10 -4

Poisson’s Ratio db b b F d. L A 0 L L F b usually decreases when L increases. Poisson’s ratio = Therefore, usually n is positive. Solids become thinner when pulled in tension. If non-compressible (constant V), then n = 0. 5.

Auxetic Materials have a Negative Poisson’s Ratio! http: //www. product-technik. co. uk/News/news. htm http: //data. bolton. ac. uk/auxnet/ /action/index. html http: //www. azom. com/details. asp? Article. ID=168

Summary of Bulk Properties Property Volume expansivity Equation of State Formula SI Units f(P, V, T) =0 K-1 f(F, L, T) =0 K-1 (3 -D) Linear expansivity (1 -D) Isothermal Bulk modulus (3 -D) f(P, V, T) =0 Young’s modulus f(F, L, T) =0 Pa = Nm-2 (1 -D) Isothermal compressibility (3 -D) f(P, V, T) =0 Pa-1 = N-1 m 2

Definition of Viscosity The top plane moves at a constant velocity, v, in response to a shear stress: y F A Dx v A There is a velocity gradient (v/y) normal to the area. The viscosity h relates the shear stress, to the velocity gradient. h has S. I. units of Pa s. Viscosity describes the resistance to flow of a fluid.

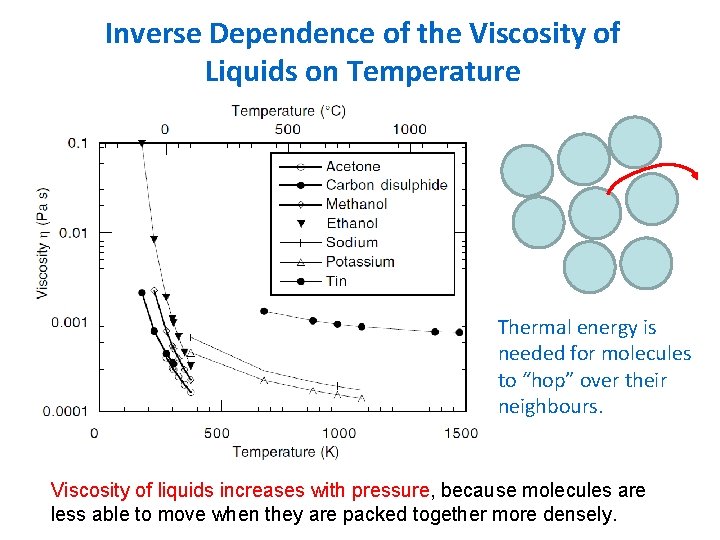
Inverse Dependence of the Viscosity of Liquids on Temperature Thermal energy is needed for molecules to “hop” over their neighbours. Viscosity of liquids increases with pressure, because molecules are less able to move when they are packed together more densely.

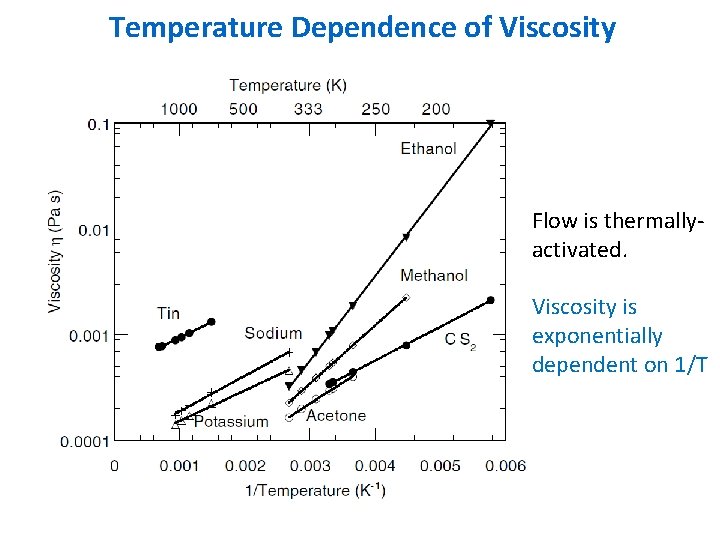
Temperature Dependence of Viscosity Flow is thermallyactivated. Viscosity is exponentially dependent on 1/T

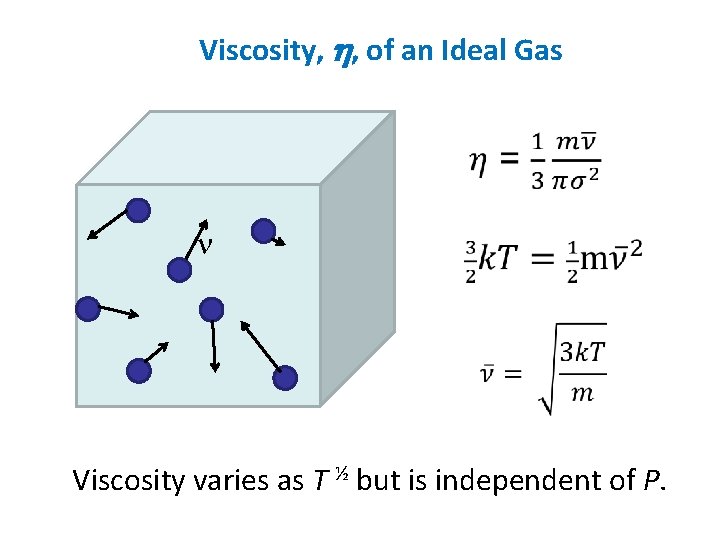
Viscosity, h, of an Ideal Gas n Viscosity varies as T ½ but is independent of P.

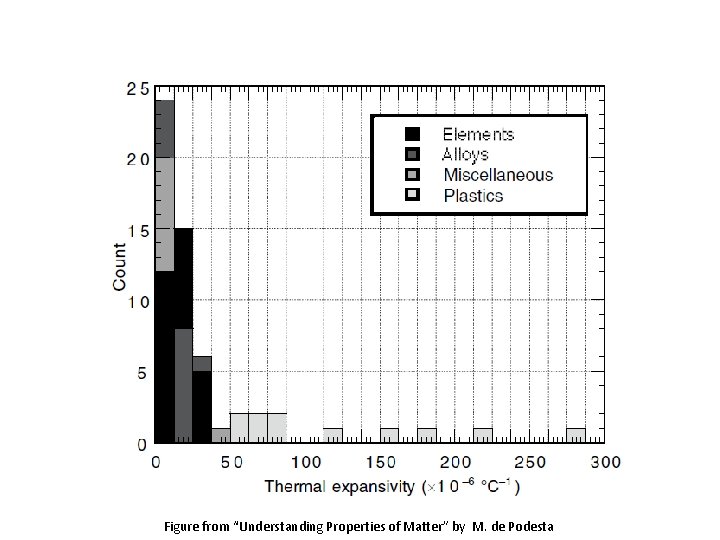
Figure from “Understanding Properties of Matter” by M. de Podesta