Photonic Crystals Periodic Surprises in Electromagnetism Steven G

Photonic Crystals: Periodic Surprises in Electromagnetism Steven G. Johnson MIT

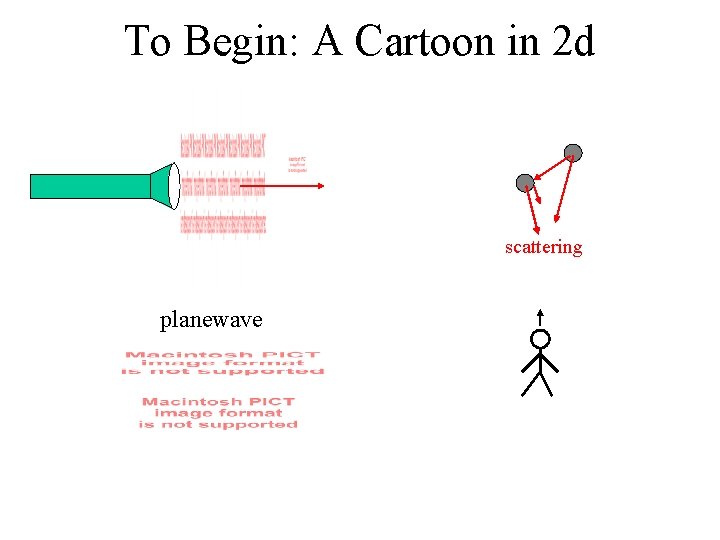
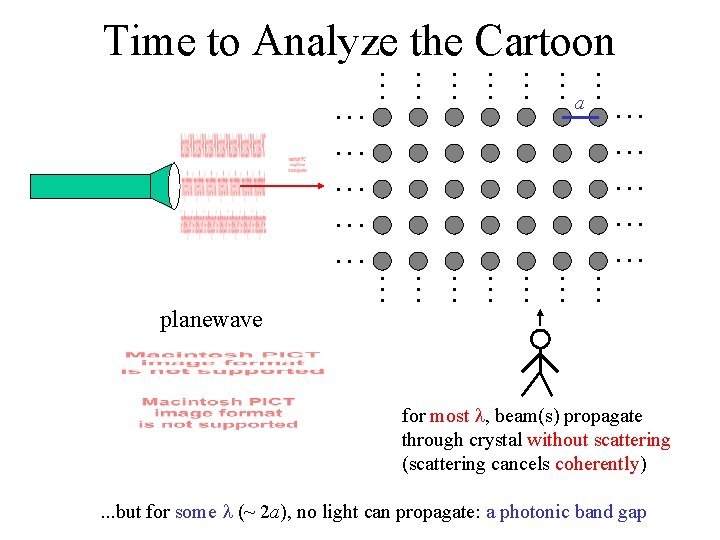
To Begin: A Cartoon in 2 d scattering planewave

To Begin: A Cartoon in 2 d a • • • • • • • • • • • • • • • • • • planewave for most l, beam(s) propagate through crystal without scattering (scattering cancels coherently). . . but for some l (~ 2 a), no light can propagate: a photonic band gap

Photonic Crystals periodic electromagnetic media 1887 1987 with photonic band gaps: “optical insulators” (need a more complex topology)

Photonic Crystals periodic electromagnetic media can trap light in cavities and waveguides (“wires”) magical oven mitts for holding and controlling light with photonic band gaps: “optical insulators”

Photonic Crystals periodic electromagnetic media But how can we understand such complex systems? Add up the infinite sum of scattering? Ugh!

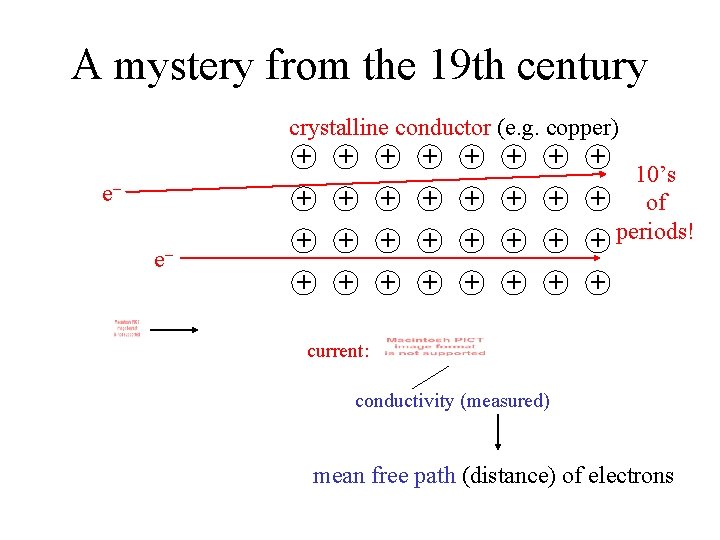
A mystery from the 19 th century conductive material + + e– + + current: conductivity (measured) mean free path (distance) of electrons

A mystery from the 19 th century crystalline conductor (e. g. copper) + + + + e– e– + + + + 10’s + of + periods! + + + + current: conductivity (measured) mean free path (distance) of electrons

A mystery solved… 1 electrons are waves (quantum mechanics) waves in a periodic medium can propagate 2 without scattering: Bloch’s Theorem (1 d: Floquet’s) The foundations do not depend on the specific wave equation.

Time to Analyze the Cartoon a • • • • • • • • • • • • • • • • • • planewave for most l, beam(s) propagate through crystal without scattering (scattering cancels coherently). . . but for some l (~ 2 a), no light can propagate: a photonic band gap

Fun with Math First task: 0 get rid of this mess dielectric function e(x) = n 2(x) + constraint eigen-operator eigen-value eigen-state

Hermitian Eigenproblems + constraint eigen-operator eigen-value eigen-state Hermitian for real (lossless) e well-known properties from linear algebra: w are real (lossless) eigen-states are orthogonal eigen-states are complete (give all solutions)

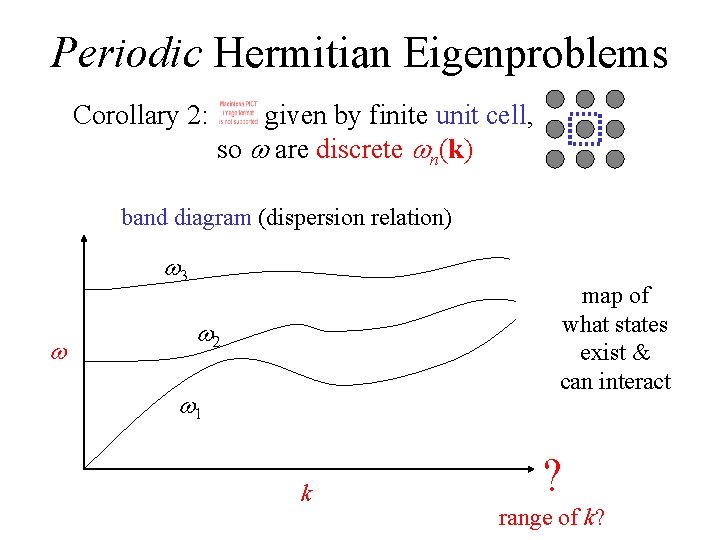
Periodic Hermitian Eigenproblems [ G. Floquet, “Sur les équations différentielles linéaries à coefficients périodiques, ” Ann. École Norm. Sup. 12, 47– 88 (1883). ] [ F. Bloch, “Über die quantenmechanik der electronen in kristallgittern, ” Z. Physik 52, 555– 600 (1928). ] if eigen-operator is periodic, then Bloch-Floquet theorem applies: can choose: planewave periodic “envelope” Corollary 1: k is conserved, i. e. no scattering of Bloch wave Corollary 2: given by finite unit cell, so w are discrete wn(k)

Periodic Hermitian Eigenproblems Corollary 2: given by finite unit cell, so w are discrete wn(k) band diagram (dispersion relation) w 3 w map of what states exist & can interact w 2 w 1 k ? range of k?

Periodic Hermitian Eigenproblems in 1 d e 1 e 2 e 1 e 2 a e(x) = e(x+a) Consider k+2π/a: k is periodic: k + 2π/a equivalent to k “quasi-phase-matching” periodic! satisfies same equation as Hk = Hk

Periodic Hermitian Eigenproblems in 1 d e 1 e 2 e 1 e 2 k is periodic: k + 2π/a equivalent to k “quasi-phase-matching” a e(x) = e(x+a) w band gap –π/a 0 π/a irreducible Brillouin zone k

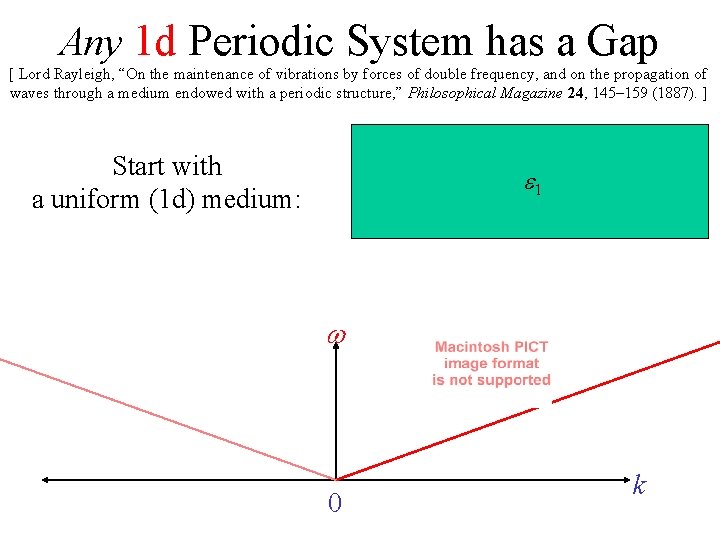
Any 1 d Periodic System has a Gap [ Lord Rayleigh, “On the maintenance of vibrations by forces of double frequency, and on the propagation of waves through a medium endowed with a periodic structure, ” Philosophical Magazine 24, 145– 159 (1887). ] Start with a uniform (1 d) medium: e 1 w 0 k

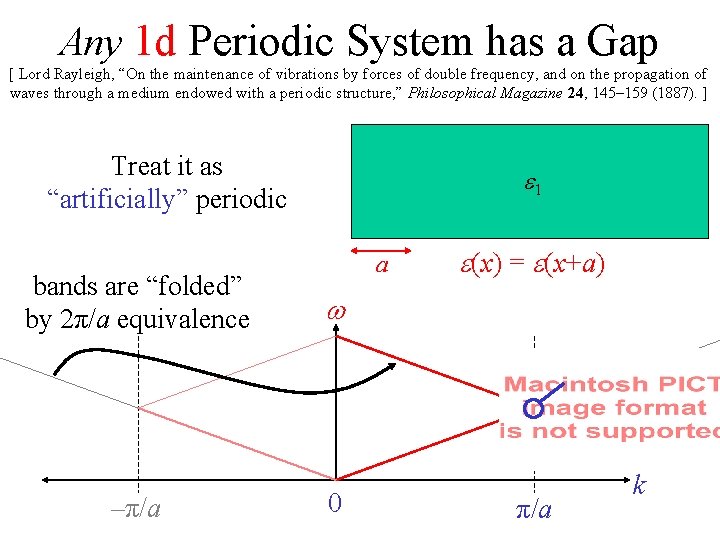
Any 1 d Periodic System has a Gap [ Lord Rayleigh, “On the maintenance of vibrations by forces of double frequency, and on the propagation of waves through a medium endowed with a periodic structure, ” Philosophical Magazine 24, 145– 159 (1887). ] Treat it as “artificially” periodic bands are “folded” by 2π/a equivalence –π/a e 1 a e(x) = e(x+a) w 0 π/a k

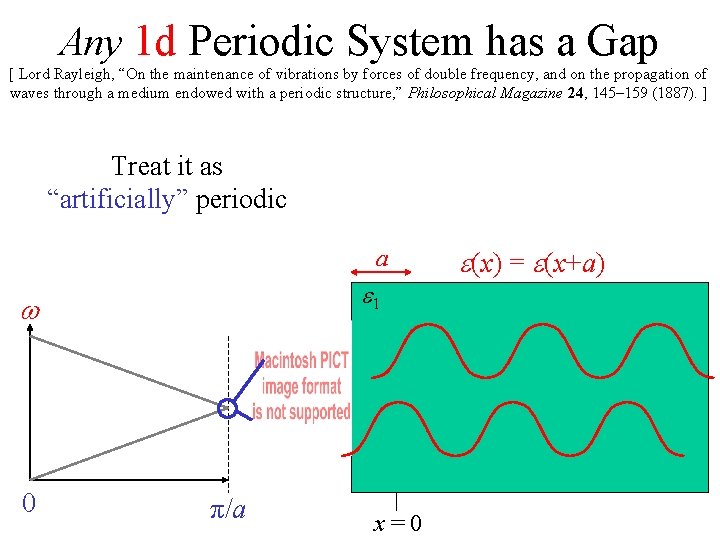
Any 1 d Periodic System has a Gap [ Lord Rayleigh, “On the maintenance of vibrations by forces of double frequency, and on the propagation of waves through a medium endowed with a periodic structure, ” Philosophical Magazine 24, 145– 159 (1887). ] Treat it as “artificially” periodic a e 1 w 0 π/a x=0 e(x) = e(x+a)

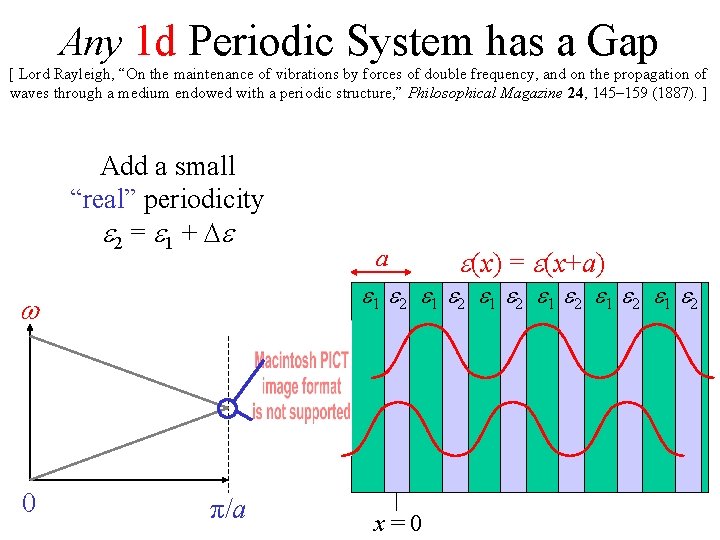
Any 1 d Periodic System has a Gap [ Lord Rayleigh, “On the maintenance of vibrations by forces of double frequency, and on the propagation of waves through a medium endowed with a periodic structure, ” Philosophical Magazine 24, 145– 159 (1887). ] Add a small “real” periodicity e 2 = e 1 + De e(x) = e(x+a) e 1 e 2 e 1 e 2 w 0 a π/a x=0

Any 1 d Periodic System has a Gap [ Lord Rayleigh, “On the maintenance of vibrations by forces of double frequency, and on the propagation of waves through a medium endowed with a periodic structure, ” Philosophical Magazine 24, 145– 159 (1887). ] Add a small “real” periodicity e 2 = e 1 + De Splitting of degeneracy: state concentrated in higher index (e 2) has lower frequency a e 1 e 2 e 1 e 2 w band gap 0 e(x) = e(x+a) π/a x=0

Some 2 d and 3 d systems have gaps • In general, eigen-frequencies satisfy Variational Theorem: “kinetic” inverse “potential” bands “want” to be in high-e …but are forced out by orthogonality –> band gap (maybe)

algebraic interlude completed… … I hope you were taking notes* [ *if not, see e. g. : Joannopoulos, Meade, and Winn, Photonic Crystals: Molding the Flow of Light ]

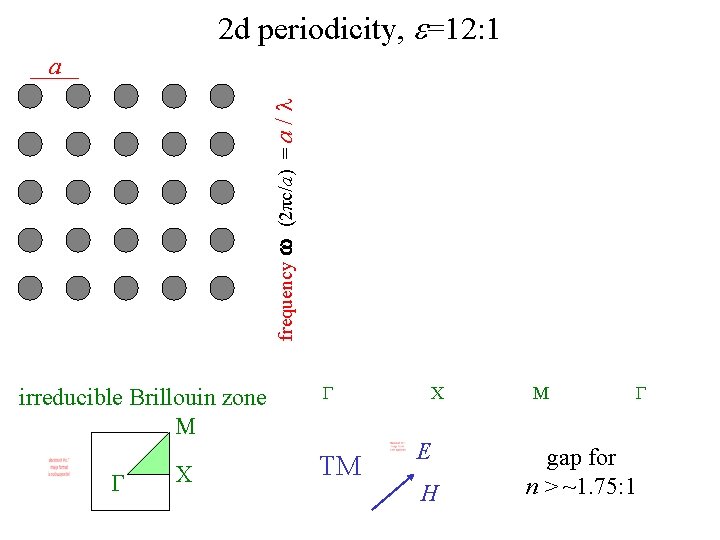
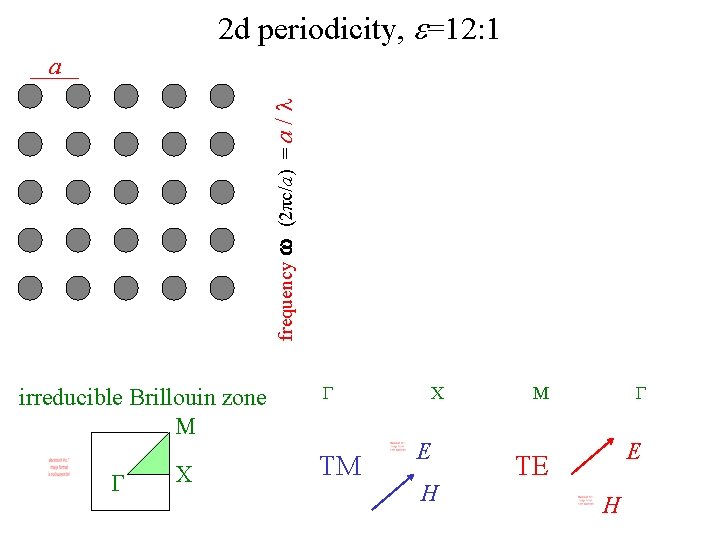
2 d periodicity, e=12: 1 frequency w (2πc/a) = a /l a irreducible Brillouin zone M G X G TM X E H M G gap for n > ~1. 75: 1

2 d periodicity, e=12: 1 Ez (+ 90° rotated version) Ez G – + TM X E H M G gap for n > ~1. 75: 1

2 d periodicity, e=12: 1 frequency w (2πc/a) = a /l a irreducible Brillouin zone M G X G TM X E H G M E TE H

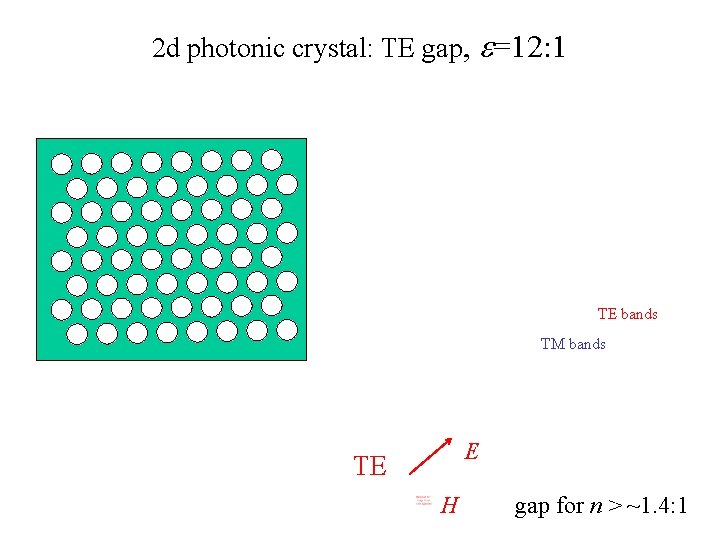
2 d photonic crystal: TE gap, e=12: 1 TE bands TM bands E TE H gap for n > ~1. 4: 1

3 d photonic crystal: complete gap , e=12: 1 I. II. gap for n > ~4: 1 [ S. G. Johnson et al. , Appl. Phys. Lett. 77, 3490 (2000) ]

You, too, can compute photonic eigenmodes! MIT Photonic-Bands (MPB) package: http: //ab-initio. mit. edu/mpb on Athena: add mpb