Photoelectric Effect Albert Einstein 1879 1955 Photoelectric effect

Photoelectric Effect Albert Einstein (1879 -1955) Photoelectric effect demonstrates the particle nature of light. (Kotz, figure 7. 6) No e- observed until light of a certain minimum E is used. Number of e- ejected does NOT depend on frequency, rather it depends on light intensity.

Photoelectric Effect (2) • Classical theory said that E of ejected electron should increase with increase in light intensity — not observed! • Experimental observations can be explained if light consists of particles called PHOTONS of discrete energy.

Atomic Line Spectra • Bohr’s greatest contribution to science was in building a simple model of the atom. • It was based on understanding the SHARP LINE SPECTRA of excited atoms. Niels Bohr (1885 -1962) (Nobel Prize, 1922)

Line Spectra of Excited Atoms • Excited atoms emit light of only certain wavelengths • The wavelengths of emitted light depend on the element. H Hg Ne

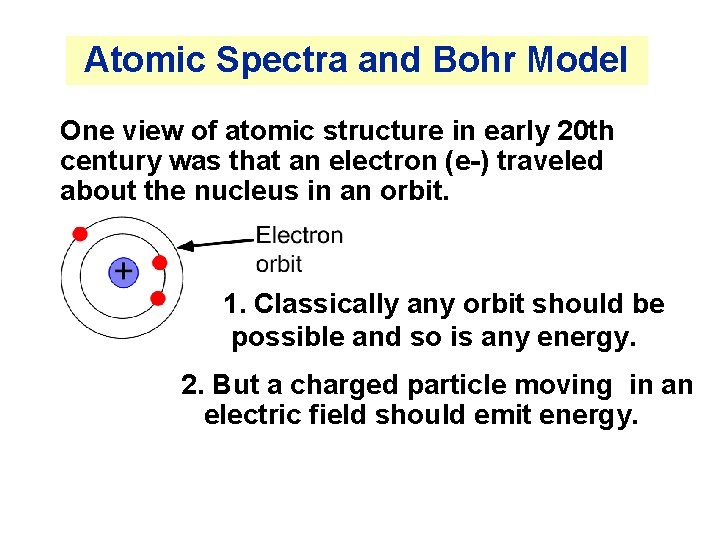
Atomic Spectra and Bohr Model One view of atomic structure in early 20 th century was that an electron (e-) traveled about the nucleus in an orbit. 1. Classically any orbit should be possible and so is any energy. 2. But a charged particle moving in an electric field should emit energy.

Atomic Spectra and Bohr Model (2) • Bohr said classical view is wrong. • Need a new theory — now called QUANTUM or WAVE MECHANICS. • e- can only exist in certain discrete orbits — called stationary states. • e- is restricted to QUANTIZED energy states. Energy of state = - C/n 2 where C is a CONSTANT n = QUANTUM NUMBER, n = 1, 2, 3, 4, . .

From Bohr model to Quantum mechanics Bohr’s theory was a great accomplishment and radically changed our view of matter. But problems existed with Bohr theory — – theory only successful for the H atom. – introduced quantum idea artificially. • So, we go on to QUANTUM or WAVE MECHANICS

Quantum or Wave Mechanics • Light has both wave & particle properties • de Broglie (1924) proposed that all moving objects have wave properties. • For light: E = hn = hc / l L. de Broglie (1892 -1987) • For particles: E = mc 2 Therefore, mc = h / l (Einstein) and for particles (mass)x(velocity) = h / l l for particles is called the de Broglie wavelength

Quantum or Wave Mechanics Schrodinger applied idea of ebehaving as a wave to the problem of electrons in atoms. Solution to WAVE EQUATION gives set of mathematical expressions called E. Schrodinger 1887 -1961 WAVE FUNCTIONS, Y Each describes an allowed energy state of an e. Quantization introduced naturally.

WAVE FUNCTIONS, Y • Y is a function of distance and two angles. • For 1 electron, Y corresponds to an ORBITAL — the region of space within which an electron is found. • Y does NOT describe the exact location of the electron. • Y 2 is proportional to the probability of finding an e- at a given point.

Uncertainty Principle W. Heisenberg 1901 -1976 Problem of defining nature of electrons in atoms solved by W. Heisenberg. Cannot simultaneously define the position and momentum (= m • v) of an electron. Dx. Dp = h At best we can describe the position and velocity of an electron by a PROBABILITY DISTRIBUTION, 2 which is given by Y

Shrödinger equation The Shrödinger equation is fundamental for describing the quantum mechanical electronic structure of matter. However, the solution of the Shrödinger equation is exceedingly expensive (scaling exponentially with number of atoms) and therefore impractical. So we should use some approximations. One of the most important approximations is the Born-Oppenheimer approximation or Hartree approximation

The properties of matter at the nanoscale are described by the laws of quantum mechanics. The behaviour of atoms and electrons is approximately governed according to the nonrelativistic Schrodinger equation. Solving this equation is difficult and only analytically possible in a few select systems, such as the hydrogen atom. To solve for a general system requires approximate computational methods.

Density Functional Theory To solve the issue of many body (many electrons. The best approximation to the ground state wavefunction is obtained by the wave-function that produces the lowest energy through DFT.

Hartree The Hartree-Fock approach seeks to approximately solve the electronic Schrödinger equation, where it assumes that the wave function can be approximated by a single Slater determinant made up of one spin orbital per electron. Since the energy expression is symmetric of the wave function. therefore determinant with the lowest energy which will predict the true wave function for the assumed functional form of a single determinant.

For single body problem For the single body problem, it can be satisfied the anti-symmetry principle by a wave function like Where x space-spin coordinates and X a spin orbital If it involved more than one body problem, It can be generalized the above solution to N electrons by using determinants therefore the equation above becomes

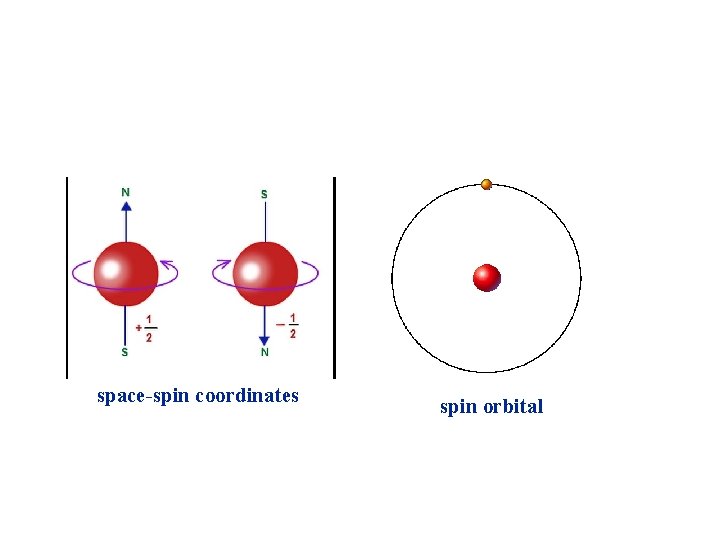
space-spin coordinates spin orbital

Now the generalization to N electrons is then easy to see, can be as simple as shown: However, unfortunately this approach cannot give precise ground state energy

Hohenberg-Kohn Theorems The many-electron wave-function is a function of 3 N variables and is too complicated to deal with. Hohenberg and Kohn proved two theorems that enable the electron density to be used instead. The first Hohenberg-Kohn theorem showed that the energy of a system is determined entirely by the system’s density. However the kinetic energy is not

The Thomas Femi Model An attempt to write a density functional for the kinetic energy is done by Thomas Femi

The Thomas Femi Model One of the main problems of the Thomas-Fermi. Dirac theory is that the kinetic energy functional is not representative of the vary in homogenous electron density in atoms and molecules. Express the kinetic energy exactly for the reference system as the sum of the expectation value of the Laplacian for each electron.

Kohn-Sham DFT The solution is to make some use of the wave-function, in the same manner as Hartree-Fock, and some use of the density. The combination of these two approaches is known as Kohn-Sham density functional theory

Born Oppenheimer Approximation The approximation of Born and Oppenheimer allows electrons and nuclei of a real system to be deal with separately due to the large mass difference between them

Exchange correlation function Local density approximation gained tremendous acceptance as result of the exchange correlation function the numerical advantages of the Exchange correlation function is the efficient methods exist for solving single-particle Schrodinger equations with a local effective potential, and there is no restriction to small systems.