Philosophy 104 Probability and Bayes Theorem Common fallacies

Philosophy 104 Probability and Bayes Theorem

Common fallacies of probability: �The Gambler’s Fallacy ◦ Is assuming that the odds of a single truly random event are affected in any way by previous iterations of the same or other truly random event.

Common fallacies of probability: �The Gambler’s Fallacy ◦ Is assuming that the odds of a single truly random event are affected in any way by previous iterations of the same or other truly random event. �Ignoring the Law of Large Numbers ◦ Is assuming there must be other explanations for very improbable events.

Which hand are you more likely to be dealt?

Which hand are you more likely to be dealt? This one? Or this one?

No… � The probability of each hand is exactly the same. � The odds of every specific five cards being dealt are the same as every other five specific cards.

Representativeness Bias focus on what represents success at poker, not on probability. � It’s true that the royal flush represents an unlikely degree of success at poker, while the nothing hand represents a common degree of failure. � Humans

Consider: � Maureen is a recent graduate of a small private college. She was active in student government, majored in English, and was the president of her sorority.

Consider: � Maureen is a recent graduate of a small private college. She was active in student government, majored in English, and was the president of her sorority. � Based on what you know, which of the following is more likely to be true of Maureen:

Consider: � Maureen is a recent graduate of a small private college. She was active in student government, majored in English, and was the president of her sorority. � Based on what you know, which of the following is more likely to be true of Maureen: ◦ She is a bank teller and a feminist

The Conjunction Fallacy � The probability of two things both being true CANNOT be higher than the probability of one of those things being true.

Consider: � You live in a house. Lightning strikes that house on average once per week. Lightning struck today (Tuesday). What is the most likely day for the next one? A. Tomorrow B. Next Tuesday C. They are all equally likely

Consider: � You live in a house. Lightning strikes that house on average once per week. Lightning struck today (Tuesday). What is the most likely day for the next one? A. Tomorrow B. Next Tuesday C. They are all equally likely � This is another instance of the conjunction fallacy.

Who is most dangerous to you? � Yourself? � Others?

Who is most dangerous to you? � Yourself? � Others? (Global murder rate: 6 ish)

Who is most dangerous to you? � Yourself? (Global suicide rate: 12 ish) � Others? (Global murder rate: 6 ish) � You’re twice as much a risk to your life as everyone else.

Who is a child safest with? � Parents? � Strangers?

Who is a child safest with? � Parents? (67% of kids murdered are killed by their parents) � Strangers? (3% of kids murdered are killed by strangers)

Moral of the story: � Humans suck at estimating probability

Two Kinds of Probability �a priori probability: ◦ The sort of probability achieved by dividing the number of desired outcomes vs. the total number of outcomes. ◦ Applies to random events. � Statistical probability: ◦ The frequency at which a given event is observed to occur. ◦ Applies to events that are not truly random.

An Example � What is the a priori probability (expressed as a percent) of a batter in baseball getting a hit in one at-bat?

An Example � What is the a priori probability (expressed as a percent) of a batter in baseball getting a hit in one at-bat? ◦ 50%

An Example � What is the a priori probability (expressed as a percent) of a batter in baseball getting a hit in one at-bat? ◦ 50% � What is the statistical probability (expressed as a percent) of a major league batter getting a hit in one at-bat?

An Example � What is the a priori probability (expressed as a percent) of a batter in baseball getting a hit in one at-bat? ◦ 50% � What is the statistical probability (expressed as a percent) of a major league batter getting a hit in one at-bat? ◦ 25. 4%

A Case Study in probability: • • • Wendy has tested positive for colon cancer. Colon cancer occurs in. 3% of the population (. 003 statistical probability) If a person has colon cancer, there is a 90% chance that they will test positive (. 9 statistical probability of a true positive) If a person does not have colon cancer, then there is a 3% chance that they will test positive (3% statistical probability of a false positive) Given that Wendy has tested positive, what is the statistical probability that she has colon cancer?

Answer: � The correct answer is 8. 3%

Answer: � The correct answer is 8. 3% � Most people (including many doctors) assume that the chances are much better than they really are that Wendy has colon cancer. The reason for this is that people tend to forget that a test must be absurdly specific to give a high probability of having a rare condition.
![Formal Statement of Bayes’s Theorem: Pr(h|e) = Pr(h) * Pr(e|h) [Pr(h) * Pr(e|h)] + Formal Statement of Bayes’s Theorem: Pr(h|e) = Pr(h) * Pr(e|h) [Pr(h) * Pr(e|h)] +](http://slidetodoc.com/presentation_image_h2/c1a7ab59bf72588f3c71735e36fe844d/image-28.jpg)
Formal Statement of Bayes’s Theorem: Pr(h|e) = Pr(h) * Pr(e|h) [Pr(h) * Pr(e|h)] + [Pr(~h) * Pr(e|~h)] h = the hypothesis e = the evidence for h Pr(h) = the statistical probability of h Pr(e|h) = the true positive rate of e as evidence for h Pr(e|~h) = the false positive rate of e as evidence for h
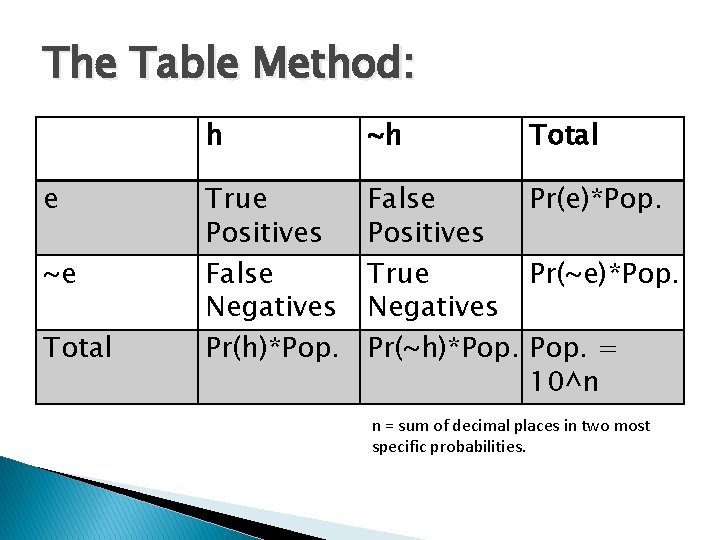
The Table Method: e ~e Total h ~h Total True Positives False Negatives Pr(h)*Pop. False Pr(e)*Pop. Positives True Pr(~e)*Pop. Negatives Pr(~h)*Pop. = 10^n n = sum of decimal places in two most specific probabilities.
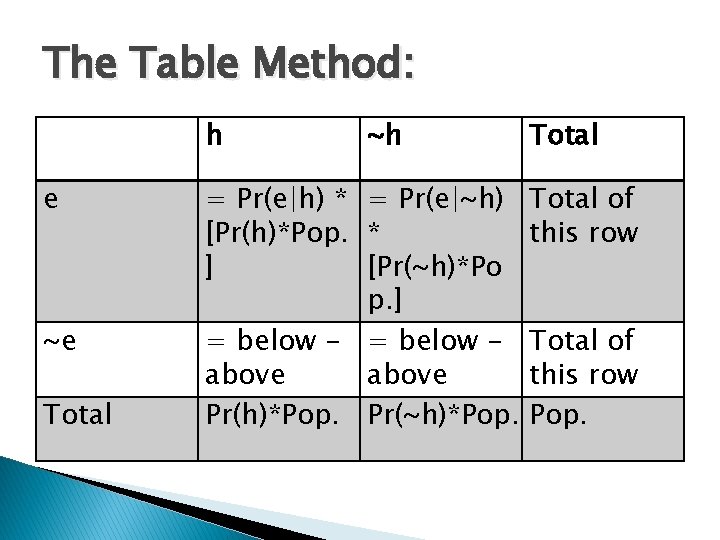
The Table Method: h e ~e Total ~h = Pr(e|h) * = Pr(e|~h) [Pr(h)*Pop. * ] [Pr(~h)*Po p. ] = below - = below above Pr(h)*Pop. Pr(~h)*Pop. Total of this row Pop.
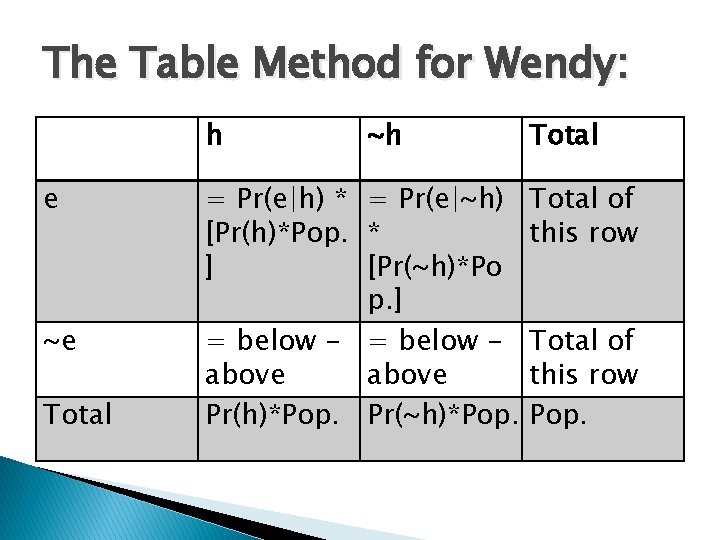
The Table Method for Wendy: h e ~e Total ~h = Pr(e|h) * = Pr(e|~h) [Pr(h)*Pop. * ] [Pr(~h)*Po p. ] = below - = below above Pr(h)*Pop. Pr(~h)*Pop. Total of this row Pop.
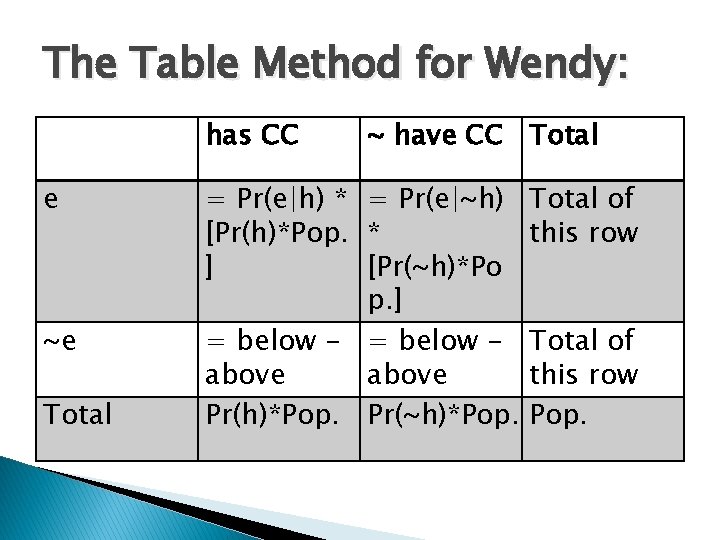
The Table Method for Wendy: has CC e ~e Total ~ have CC Total = Pr(e|h) * = Pr(e|~h) [Pr(h)*Pop. * ] [Pr(~h)*Po p. ] = below - = below above Pr(h)*Pop. Pr(~h)*Pop. Total of this row Pop.
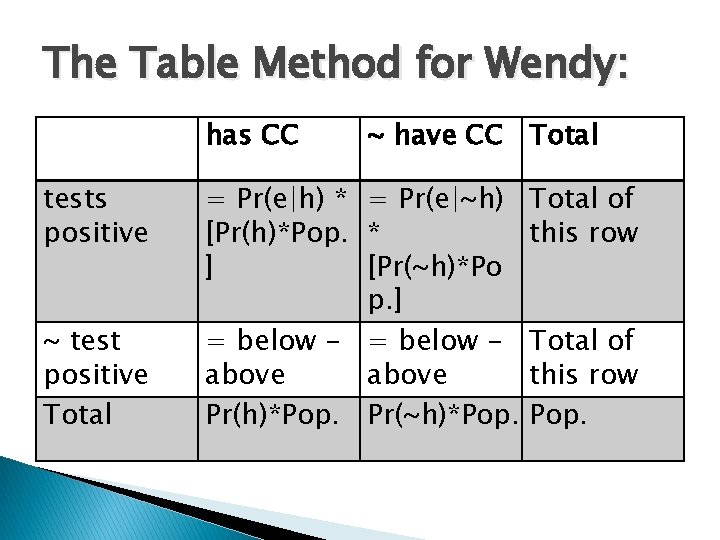
The Table Method for Wendy: has CC tests positive ~ test positive Total ~ have CC Total = Pr(e|h) * = Pr(e|~h) [Pr(h)*Pop. * ] [Pr(~h)*Po p. ] = below - = below above Pr(h)*Pop. Pr(~h)*Pop. Total of this row Pop.
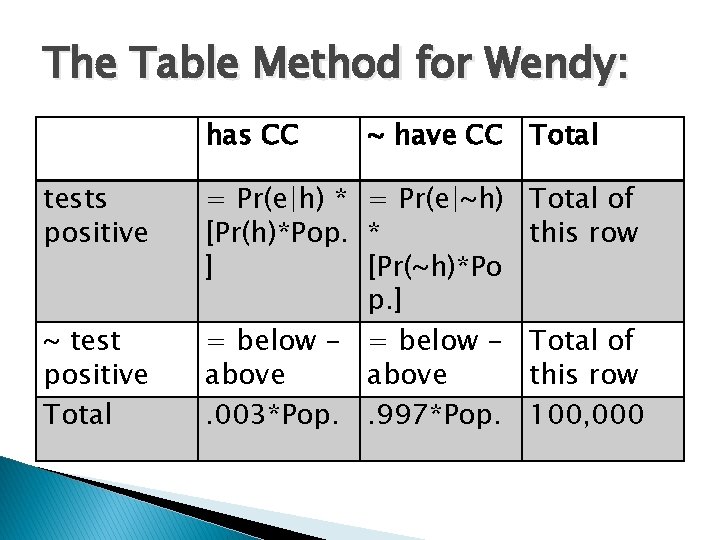
The Table Method for Wendy: has CC tests positive ~ test positive Total ~ have CC Total = Pr(e|h) * = Pr(e|~h) [Pr(h)*Pop. * ] [Pr(~h)*Po p. ] = below - = below above. 003*Pop. . 997*Pop. Total of this row 100, 000
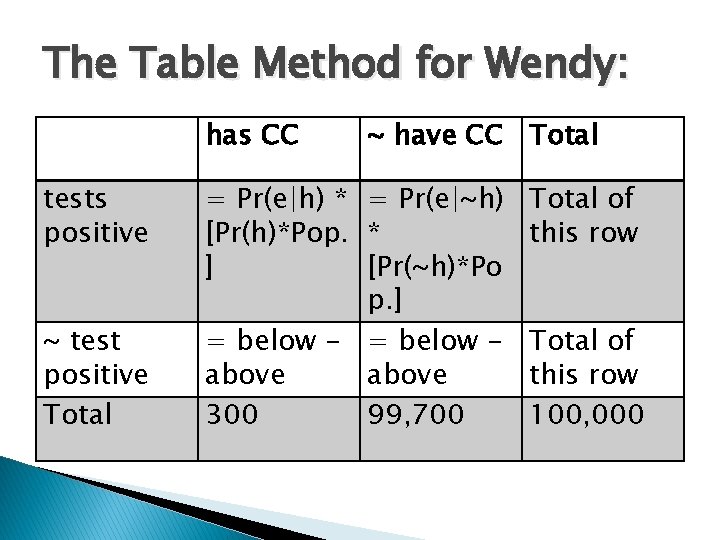
The Table Method for Wendy: has CC tests positive ~ test positive Total ~ have CC Total = Pr(e|h) * = Pr(e|~h) [Pr(h)*Pop. * ] [Pr(~h)*Po p. ] = below - = below above 300 99, 700 Total of this row 100, 000
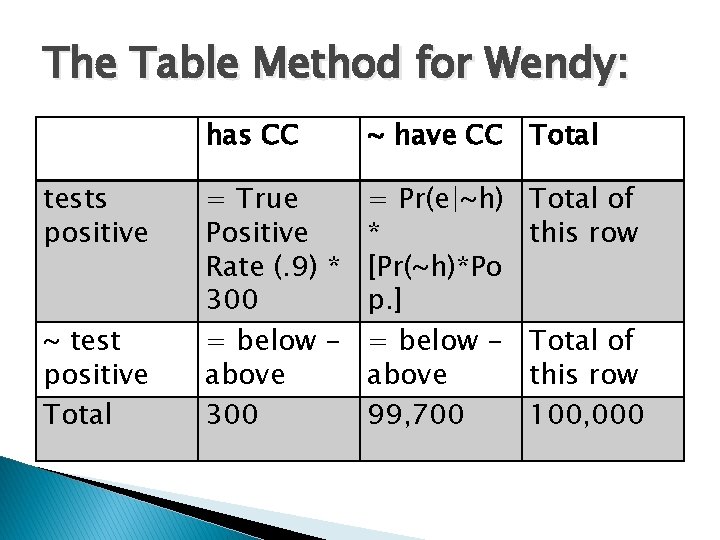
The Table Method for Wendy: tests positive ~ test positive Total has CC ~ have CC Total = True Positive Rate (. 9) * 300 = below above 300 = Pr(e|~h) * [Pr(~h)*Po p. ] = below above 99, 700 Total of this row 100, 000
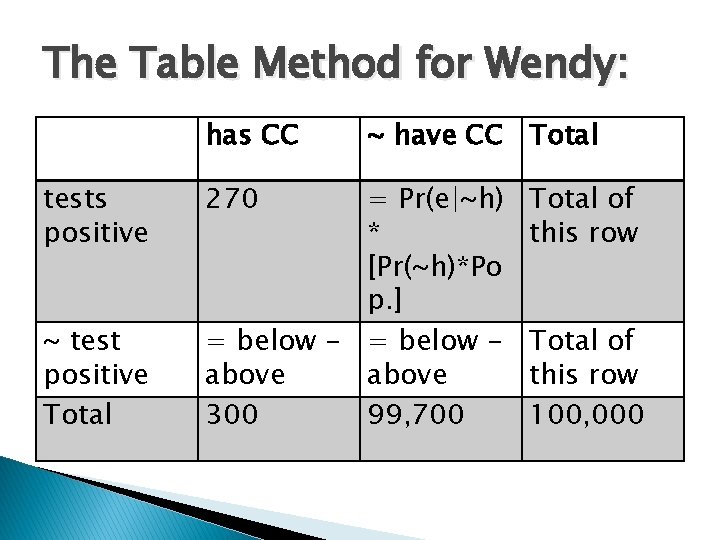
The Table Method for Wendy: has CC tests positive ~ test positive Total 270 ~ have CC Total = Pr(e|~h) * [Pr(~h)*Po p. ] = below - = below above 300 99, 700 Total of this row 100, 000
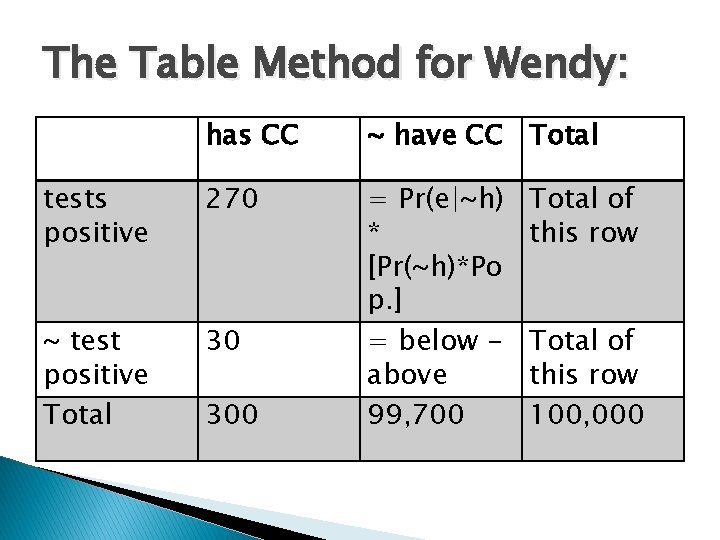
The Table Method for Wendy: has CC ~ have CC Total tests positive 270 ~ test positive Total 30 = Pr(e|~h) * [Pr(~h)*Po p. ] = below above 99, 700 300 Total of this row 100, 000
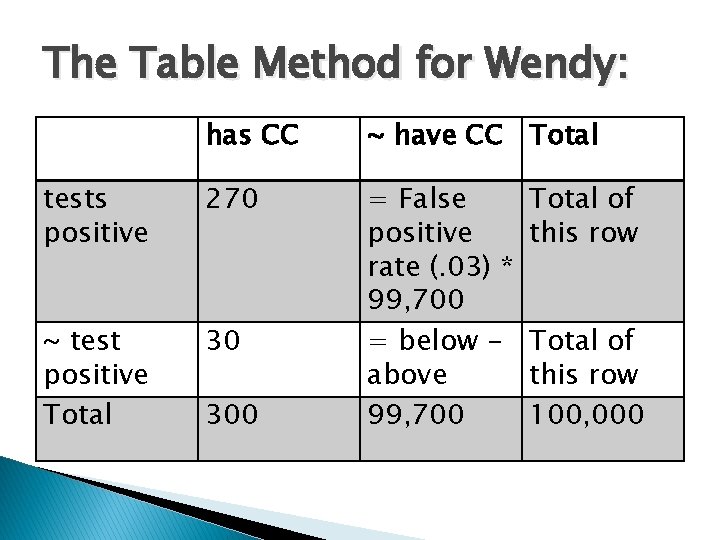
The Table Method for Wendy: has CC ~ have CC Total tests positive 270 ~ test positive Total 30 = False positive rate (. 03) * 99, 700 = below above 99, 700 300 Total of this row 100, 000
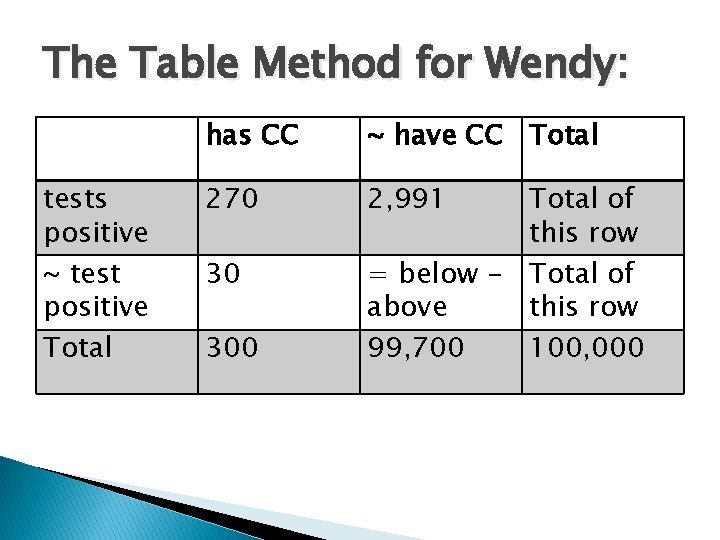
The Table Method for Wendy: tests positive ~ test positive Total has CC ~ have CC Total 270 2, 991 30 300 Total of this row = below - Total of above this row 99, 700 100, 000
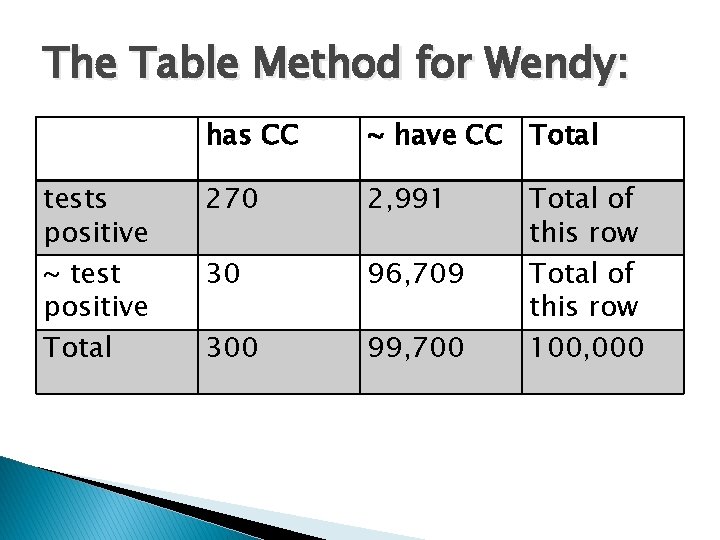
The Table Method for Wendy: tests positive ~ test positive Total has CC ~ have CC Total 270 2, 991 30 96, 709 300 99, 700 Total of this row 100, 000
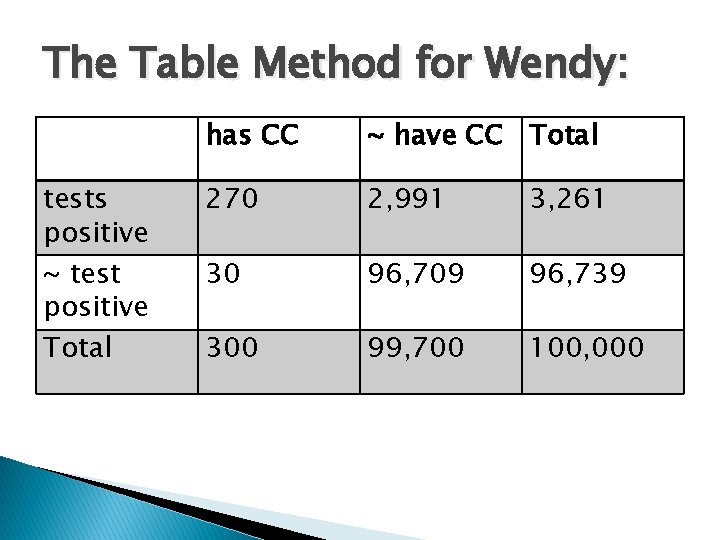
The Table Method for Wendy: tests positive ~ test positive Total has CC ~ have CC Total 270 2, 991 3, 261 30 96, 709 96, 739 300 99, 700 100, 000
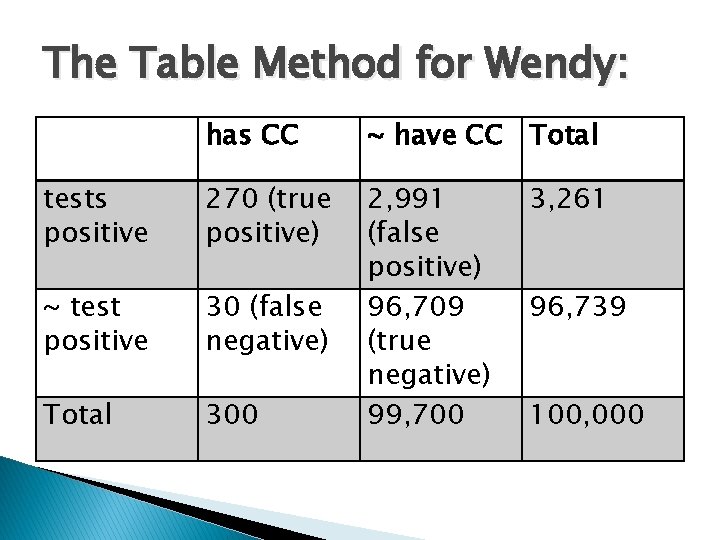
The Table Method for Wendy: has CC ~ have CC Total tests positive 270 (true positive) ~ test positive 30 (false negative) Total 300 2, 991 (false positive) 96, 709 (true negative) 99, 700 3, 261 96, 739 100, 000

What are Wendy’s chances? tests positive has CC 270 (true positive) ~ have CC 2, 991 (false positive) Total 3, 261 • Wendy’s Chances given that she tests positive are the true positives divided by the number of total tests. That is, 270/3261, which is. 083 (8. 3%). • Those who misestimate that probability forget that colon cancer is rarer than a false positive on a test.

How about a second test? �Note that testing positive (given the test accuracy specified) raises one’s chances of having the condition from. 003(the base rate) to. 083. �If we use. 083 as the new base rate, those who again test positive then have a 73. 1% chance of having the condition. �A third positive test (with. 731 as the new base rate) raises the chance of having the condition to 98. 8%
- Slides: 45