Phasor Relationships for Circuit Elements 8 4 Impedance



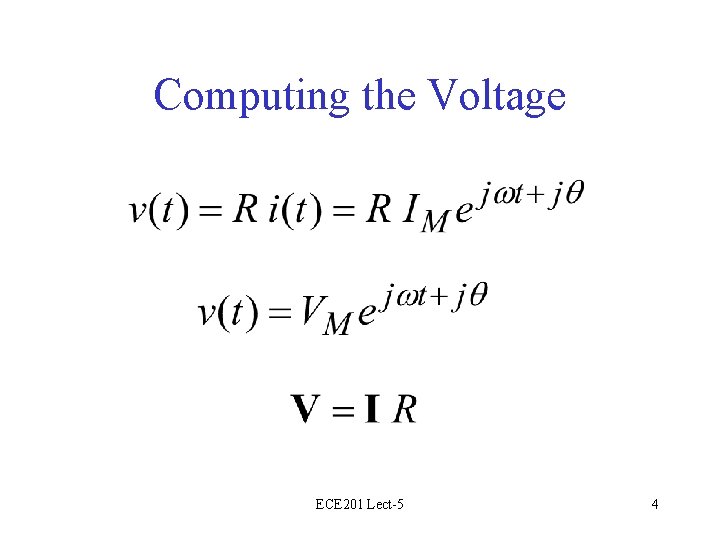























- Slides: 29

Phasor Relationships for Circuit Elements (8. 4); Impedance and Admittance (8. 5) Dr. Holbert February 1, 2006 ECE 201 Lect-5 1

Phasor Relationships for Circuit Elements • Phasors allow us to express current-voltage relationships for inductors and capacitors much like we express the current-voltage relationship for a resistor. • A complex exponential is the mathematical tool needed to obtain this relationship. ECE 201 Lect-5 2

I-V Relationship for a Resistor + i(t) v(t) R – Suppose that i(t) is a sinusoid: i(t) = IM ej(wt+q) Find v(t) ECE 201 Lect-5 3
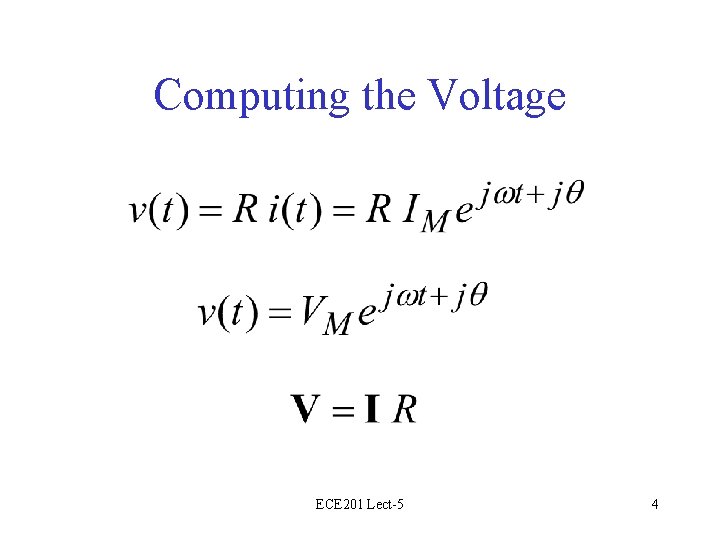
Computing the Voltage ECE 201 Lect-5 4

Class Example • Learning Extension E 8. 5 ECE 201 Lect-5 5

I-V Relationship for a Capacitor + i(t) v(t) C – Suppose that v(t) is a sinusoid: v(t) = VM ej(wt+q) Find i(t) ECE 201 Lect-5 6

Computing the Current ECE 201 Lect-5 7

Phasor Relationship • Represent v(t) and i(t) as phasors: V = VM q I = j C V • The derivative in the relationship between v(t) and i(t) becomes a multiplication by j in the relationship between V and I. ECE 201 Lect-5 8

Example v(t) = 120 V cos(377 t + 30 ) C = 2 m. F • What is V? • What is I? • What is i(t)? ECE 201 Lect-5 9

Class Example • Learning Extension E 8. 7 ECE 201 Lect-5 10

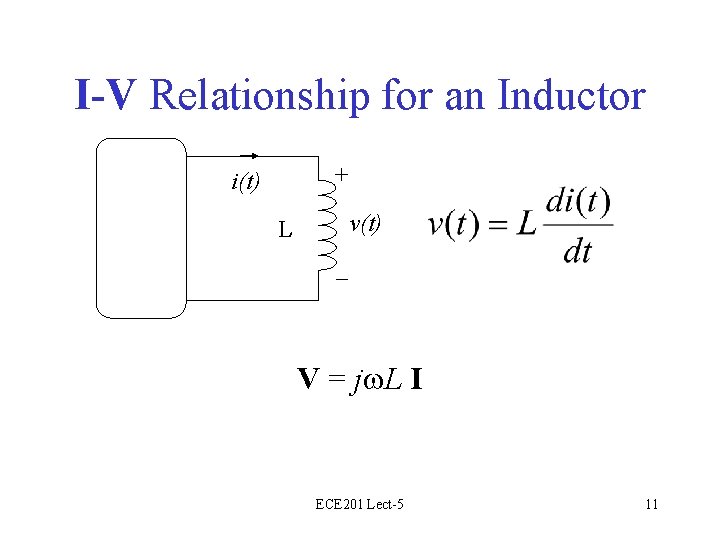
I-V Relationship for an Inductor + i(t) v(t) L – V = j L I ECE 201 Lect-5 11

Example i(t) = 1 m. A cos(2 9. 15 • 107 t + 30 ) L = 1 m. H • What is I? • What is V? • What is v(t)? ECE 201 Lect-5 12

Class Example • Learning Extension E 8. 6 ECE 201 Lect-5 13

Circuit Element Phasor Relations (ELI and ICE man) ECE 201 Lect-5 14

Impedance • AC steady-state analysis using phasors allows us to express the relationship between current and voltage using a formula that looks likes Ohm’s law: V=IZ • Z is called impedance (units of ohms, W) ECE 201 Lect-5 15

Impedance • Resistor: V=IR – The impedance is ZR = R • Inductor: V = I j L – The impedance is ZL = j L ECE 201 Lect-5 16

Impedance • Capacitor: – The impedance is ZC = 1/j C ECE 201 Lect-5 17

Some Thoughts on Impedance • • Impedance depends on the frequency, =2 f Impedance is (often) a complex number. Impedance is not a phasor (why? ). Impedance allows us to use the same solution techniques for AC steady state as we use for DC steady state. ECE 201 Lect-5 18

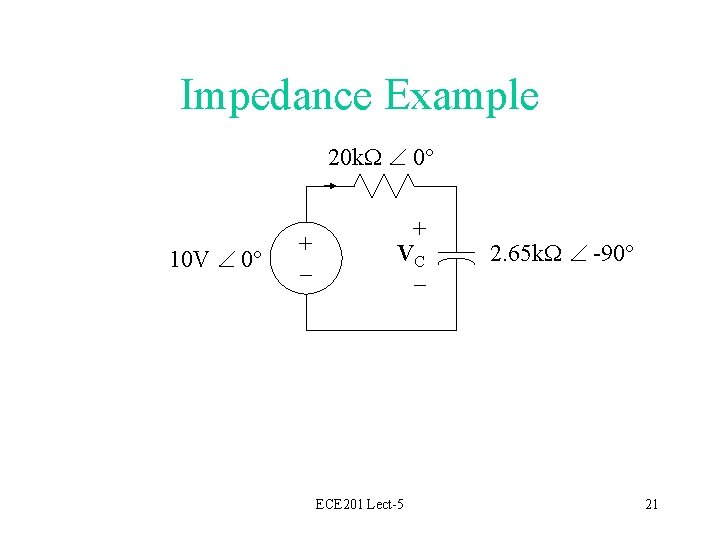
Impedance Example: Single Loop Circuit 20 k. W 10 V 0 + – 1 m. F + – VC = 377 Find VC ECE 201 Lect-5 19

Impedance Example • How do we find VC? • First compute impedances for resistor and capacitor: ZR = 20 k. W 0 ZC = 1/j (377· 1 m. F) = 2. 65 k. W -90 ECE 201 Lect-5 20

Impedance Example 20 k. W 0 10 V 0 + – + VC – ECE 201 Lect-5 2. 65 k. W -90 21

Impedance Example Now use the voltage divider to find VC: ECE 201 Lect-5 22

Low Pass Filter: A Single Node-pair Circuit + 5 m. A 0 0. 1 m. F 1 k. W V – Find v(t) for =2 3000 ECE 201 Lect-5 23

Find Impedances + -j 530 W 5 m. A 0 V 1 k. W ECE 201 Lect-5 – 24

Find the Equivalent Impedance + 5 m. A 0 Zeq V – ECE 201 Lect-5 25

Parallel Impedances ECE 201 Lect-5 26

Computing V ECE 201 Lect-5 27

Impedance Summary ECE 201 Lect-5 28

Class Examples • Learning Extension E 8. 8 • Learning Extension E 8. 9 ECE 201 Lect-5 29