Phases of Matter The Phases of Matter are



















































- Slides: 70


Phases of Matter • The Phases of Matter are related directly to the amount of energy the matter contains. – Energy occurs in 2 forms: • Kinetic: the energy of movement • Potential: stored energy • Phases are determined by how much kinetic energy the matter has. • There are 4 phases of matter: Solid, liquid, gas, and plasma. – Some say plasma is NOT a form of matter; we will count it.

Phases of Matter • The first phase of matter is SOLID. – The most orderly form of matter. • • • Shape: Definite Volume: Definite Energy: Low Entropy: Low Intermolecular Forces: Strong

Phases of Matter – Liquids are the next phase of matter. – The second most orderly form of matter. • • • Shape: Indefinite Volume: Definite Energy: Medium Entropy: Medium Intermolecular Forces: Medium

Phases of Matter: • Gases are third phase of matter – Shape: Indefinite – Volume: Indefinite – Energy: High – Entropy: High – Intermolecular Forces: Very weak (almost nonexistent) * Molecules that are spaced far apart and can move freely * Because of this, pressure and temperature can affect the volume of a gas in ways that it would not affect another phase of matter

Phases of Matter: • Plasmas are the next phase of matter. • They are found only in stars and, in theory, fusion reactors. The least orderly form of matter. – – – Shape: Indefinite Volume: Indefinite Energy: Very High Entropy: Very High Intermolecular Forces: Nonexistent

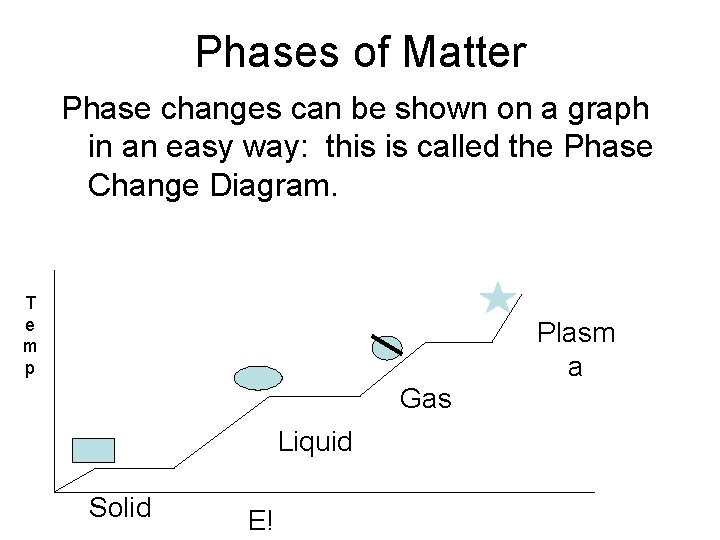
Phases of Matter Phase changes can be shown on a graph in an easy way: this is called the Phase Change Diagram. T e m p Plasm a Gas Liquid Solid E!

Phase Change Diagram • Temperature does not change during a phase change– but ENERGY does. • Instead of the e! adding to temperature, e! is used to break attractions between molecules. • In ice, e! works to vibrate the molecules beyond vibrating. In water, it works to spread the molecules out far enough that their density decreases enough to escape into the air.

Thermodynamics • The study of heat/energy as it moves through a system – Phase changes: Melting = Freezing? • Yes-- in one, energy is being added (melting); in the other, it’s being taken away (freezing) • Calculated using Calorimetry – Uses masses and temperature changes to determine energy flow

Calorimetry • Energy can be calculated using the formula: Q = m x c x ∆T Where: Q = energy (joules, kilojoules, or calories) m = mass in g c = Specific Heat (more) ∆T = Change in Temperature (K or o. C)

Specific Heat • Term given for the amount of energy needed to raise 1 g of a substance a given temperature: – For water, c = 1 cal / g o. C – Also c = 4. 18 j / g o. C • From which we can deduce: – 1 cal = 4. 18 j

For Ice? Steam? • Ice’s Specific Heat: – 2. 09 j/g o. C • Steam’s Specific Heat: – 1. 84 j/g o. C

Energy of a Phase Change • Heat of Fusion: The amount of heat required to MELT a solid; – Also, the heat given off by freezing a liquid • For H 2 O: 333 j / g • Heat of Vaporization: The amount of heat needed to BOIL a liquid; – Also, the heat given off by condensing a gas • For H 2 O: 2230 j / g

Temperature and Pressure Temperature – a measure of the kinetic energy of molecules * Kinetic energy – the energy of movement * Measured in Kelvin (K) Pressure - force exerted on a surface area *Comes from molecules colliding *Measured in atmospheres (atm)

Standard Temperature and Pressure (STP) Standard temperature 273 K Standard pressure 1 atm Conversion Factor: 1 atm = 101. 3 k. Pa = 760 mm. Hg K = °C + 273 Ex: Convert 25°C to Kelvin 25°C + 273 = 298 K Ex: How many k. Pa is 1. 37 atm? 1. 37 atm x (101. 3 k. Pa/1 atm) = 139 k. Pa Ex: How many atm are in 231. 5 mm. Hg? 231. 5 mm Hg x (1 atm/760 mm Hg) =0. 3046 atm

Boyle’s Law • As the pressure on a gas increases the volume decreases 1 atm 2 atm 4 Liters 2 • Pressure and volume are inversely related

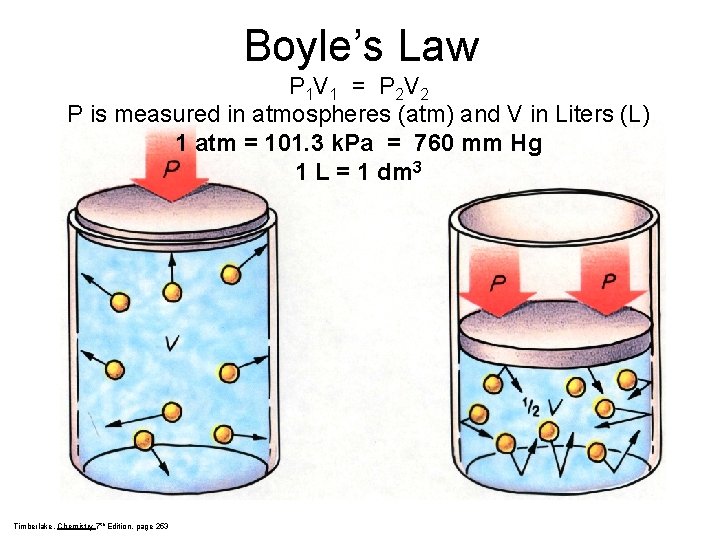
Boyle’s Law P 1 V 1 = P 2 V 2 P is measured in atmospheres (atm) and V in Liters (L) 1 atm = 101. 3 k. Pa = 760 mm Hg 1 L = 1 dm 3 Timberlake, Chemistry 7 th Edition, page 253

Boyle's Law Pressure goes up as Volume goes down. Why? As pressure increases, gas particles are forced closer together. This decreases the gas’ volume A bicycle pump is a good example of Boyle's law. As the volume of the air trapped in the pump is reduced, its pressure goes up, and air is forced into the tire. Robert Boyle (1627 - 1691) Son of Early of Cork, Ireland.

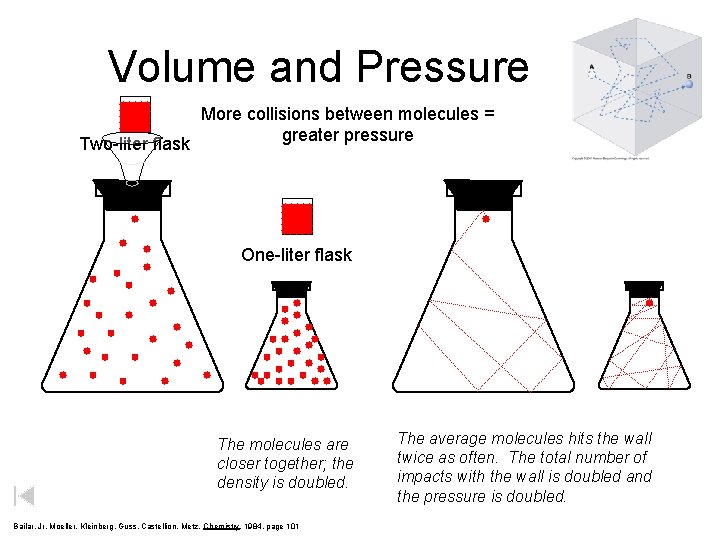
Volume and Pressure More collisions between molecules = greater pressure Two-liter flask One-liter flask The molecules are closer together; the density is doubled. Bailar, Jr, Moeller, Kleinberg, Guss, Castellion, Metz, Chemistry, 1984, page 101 The average molecules hits the wall twice as often. The total number of impacts with the wall is doubled and the pressure is doubled.

PV Calculation (Boyle’s Law) A quantity of gas has a volume of 120 L when confined under a pressure of 0. 90 atm. At what pressure will the gas be if the volume is decreased to 30 L? P 1 x V 1 = P 2 x V 2 (0. 90 atm) x (120 L) = (P 2) x (30 L) P 2 = 3. 6 atm = 4 atm

Charles’ Law V 1 V 2 = T 1 T 2 Timberlake, Chemistry 7 th Edition, page 259

Charles' Law Temperature goes up as Volume goes up. V and T are directly related. A hot air balloon is a good example of Charles's law. V 1 V 2 = T 1 T 2 Where Volume is measures in L and Temperature is measured in Kelvin (K) K= Celsius + 273 Jacques Charles (1746 - 1823) Isolated boron and studied gases. Balloonist.

Temperature • Raising the temperature of a gas increases the pressure if the volume is held constant. • The molecules move faster and hit the walls harder. • If the pressure is held constant, raising the temperature of a gas increases the volume

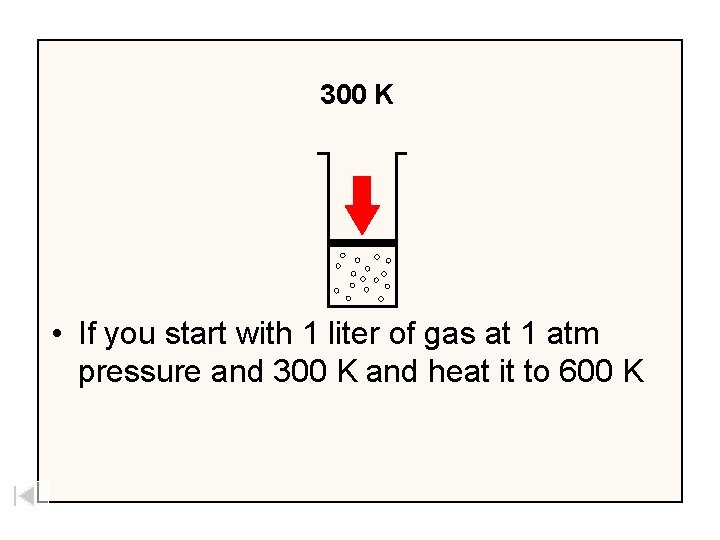
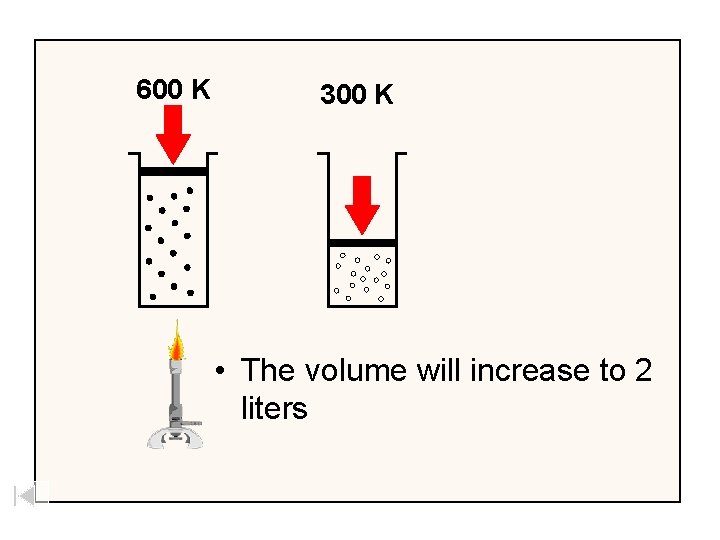
300 K • If you start with 1 liter of gas at 1 atm pressure and 300 K and heat it to 600 K

600 K 300 K • The volume will increase to 2 liters

VT Calculation (Charles’ Law) At constant pressure, the volume of a gas is increased from 150 L to 300 L by heating it. If the original temperature of the gas was 20 o. C, what will its final temperature be? T 1 T 2 V 1 V 2 = = 20 o. C + 273 = 293 K XK 150 L 300 L 150 L 293 K = 300 L T 2 = 586 K

Combined Gas Law It’s difficult to change the volume of a gas without changing the volume AND the pressure. This leads to Combined Gas Law. Note: STP = Standard Temperature and Pressure = 273 K and 1 atm

The Combined Gas Law (This “gas law” comes from “combining” Boyle‘s and Charles’ law) P = pressure (any unit will work as long as it’s the same on both sides) V = volume (any unit will work as long as it’s the same on both sides) T = temperature (must be in Kelvin) 1 = initial conditions 2 = final conditions

The Combined Gas Law When measured at STP, a quantity of gas has a volume of 500 L. What volume will it occupy at 10 o. C and 0. 90 atm? (1 atm) x (500 L) = (0. 90) x (V 2) 273 K 283 K 1. 83 = (0. 90 x. V 2)/283 P 1 = T 1 = V 1 = P 2 = T 2 = V 2 = 1 atm 518 = 0. 90 x. V 2 273 K 500 L V 2 = 575 L = 600 L 0. 90 atm 10 o. C + 273 = 283 K XL

A sample of methane occupies 126 dm 3 at -75 o. C and 985 mm Hg. Find its volume at STP. T 1 = -75 o. C + 273 = 198 K P 1 V 1 T 1 = P 2 V 2 985 mm Hg (126 dm 3) T 2 198 K = 760 mm Hg (V 2) 273 K Cross-multiply and divide: 985 (126) (273) = 198 (760) V 2 = 225 dm 3

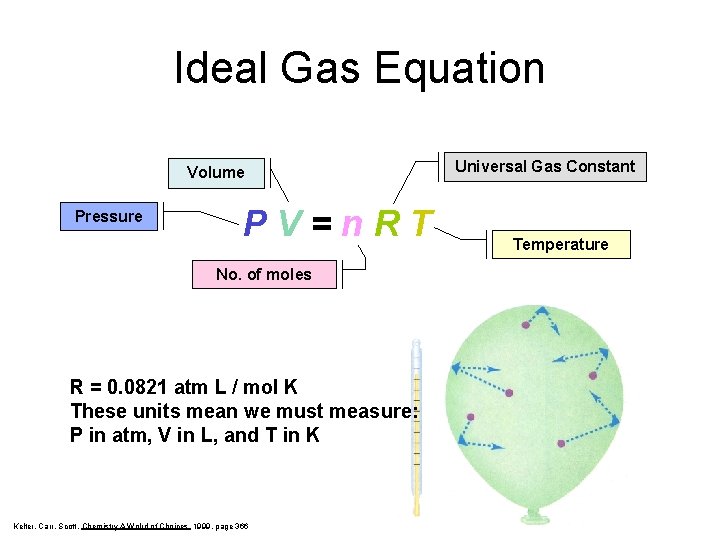
Ideal Gas Law PV = n. RT Takes into account the number of molecules of a gas (moles).

Ideal Gas Equation Volume Pressure PV=n. RT No. of moles R = 0. 0821 atm L / mol K These units mean we must measure: P in atm, V in L, and T in K Kelter, Carr, Scott, Chemistry A Wolrd of Choices 1999, page 366 Universal Gas Constant Temperature

Ideal Gas Law What is the volume that 500 g of iodine will occupy under the conditions: Temp = 300 o. C and Pressure = 740 mm Hg? Step 1) Write down given information. mass = 500 g iodine T = 300 o. C P = 740 mm Hg R = 0. 0821 atm. L / mol. K Step 2) Equation: PV = n. RT Step 3) Solve for variable V = n. RT P Step 4) Substitute in numbers and solve (500 g)(0. 0821 atm. L / mol. K)(300 o. C) V = 740 mm Hg V= What MISTAKES did we make in this problem?

What mistakes did we make in this problem? What is the volume that 500 g of iodine will occupy under the conditions: Temp = 300 o. C and Pressure = 740 mm Hg? Step 1) Write down given information. mass = 500 g iodine Convert mass to gram; recall iodine is diatomic (I 2) x mol I 2 = 500 g I 2(1 mol I 2 / 254 g I 2) n = 1. 9685 mol I 2 T = 300 o. C Temperature must be converted to Kelvin T = 300 o. C + 273 T = 573 K P = 740 mm Hg Pressure needs to have same unit as R; therefore, convert pressure from mm Hg to atm. x atm = 740 mm Hg (1 atm / 760 mm Hg) P = 0. 8 atm R = 0. 0821 atm. L / mol. K

Ideal Gas Law What is the volume that 500 g of iodine will occupy under the conditions: Temp = 300 o. C and Pressure = 740 mm Hg? Step 1) Write down given information. mass = 500 g iodine n = 1. 9685 mol I 2 T = 573 K (300 o. C) P = 0. 9737 atm (740 mm Hg) R = 0. 0821 atm. L / mol. K V=? L Step 2) Equation: PV = n. RT Step 3) Solve for variable V = n. RT P Step 4) Substitute in numbers and solve (1. 9685 mol)(0. 0821 atm. L / mol. K)(573 K) V = 0. 9737 atm V = 95. 1 L I 2 = 100 L I 2

Dalton’s Law of Partial Pressures

Dalton’s Law The total pressure of a mixture of gases equals the sum of the partial pressures of the individual gases when the gases are at equal volume. Ptotal = P 1 + P 2 +. . . Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Partial Pressures In a gaseous mixture, a gas’s partial pressure is the one the gas would exert if it were by itself in the container. 200 k. Pa + 500 k. Pa + 400 k. Pa = ? k. Pa 1100 k. Pa

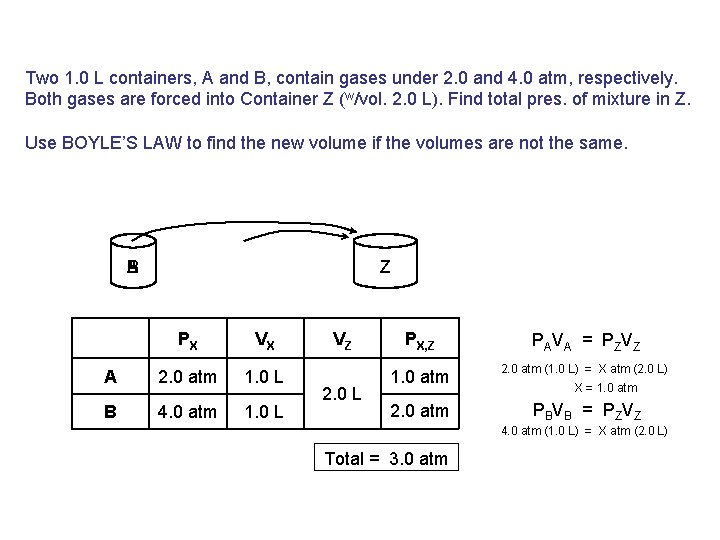
Two 1. 0 L containers, A and B, contain gases under 2. 0 and 4. 0 atm, respectively. Both gases are forced into Container Z (w/vol. 2. 0 L). Find total pres. of mixture in Z. Use BOYLE’S LAW to find the new volume if the volumes are not the same. B A Z PX VX A 2. 0 atm 1. 0 L B 4. 0 atm 1. 0 L VZ 2. 0 L PX, Z PAVA = PZVZ 1. 0 atm 2. 0 atm (1. 0 L) = X atm (2. 0 L) 2. 0 atm PBVB = PZVZ X = 1. 0 atm 4. 0 atm (1. 0 L) = X atm (2. 0 L) Total = 3. 0 atm

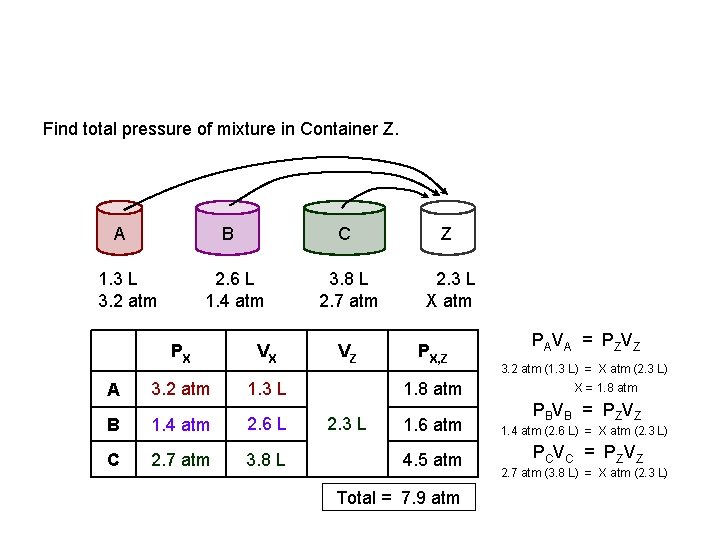
Find total pressure of mixture in Container Z. A B 1. 3 L 3. 2 atm A 2. 6 L 1. 4 atm PX VX 3. 2 atm 1. 3 L B 1. 4 atm 2. 6 L C 2. 7 atm 3. 8 L C Z 3. 8 L 2. 7 atm 2. 3 L X atm VZ PX, Z 1. 8 atm 2. 3 L PAVA = PZVZ 3. 2 atm (1. 3 L) = X atm (2. 3 L) X = 1. 8 atm PBVB = PZVZ 1. 6 atm 1. 4 atm (2. 6 L) = X atm (2. 3 L) 4. 5 atm P C V C = P ZV Z Total = 7. 9 atm 2. 7 atm (3. 8 L) = X atm (2. 3 L)

Diffusion

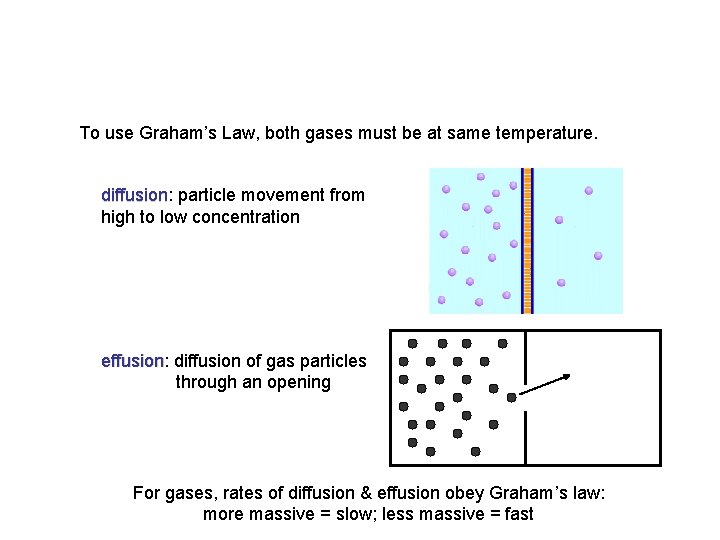
Diffusion vs. Effusion Diffusion - The tendency of the molecules of a given substance to move from regions of higher concentration to regions of lower concentration Examples: A scent spreading throughout a room or people entering a theme park Effusion - The process by which gas particles under pressure pass through a tiny hole Examples: Air slowly leaking out of a tire or helium leaking out of a balloon

Effusion Particles in regions of high concentration spread out into regions of low concentration, filling the space available to them.

Graham’s Law of Diffusion

Gas Diffusion and Effusion Graham's law governs effusion and diffusion of gas molecules. Rate of effusion is inversely proportional to its molar mass. (Heavier gases move slower) Thomas Graham (1805 - 1869)

To use Graham’s Law, both gases must be at same temperature. diffusion: diffusion particle movement from high to low concentration NET MOVEMENT effusion: effusion diffusion of gas particles through an opening For gases, rates of diffusion & effusion obey Graham’s law: more massive = slow; less massive = fast

Graham’s Law • The rate of diffusion/effusion is proportional to the mass of the molecules 80 g 250 g Large molecules move slower than small molecules

On average, carbon dioxide travels at 410 m/s at 25 o. C. Find the average speed of chlorine at 25 o. C. **Hint: Put whatever you’re looking for in the numerator.

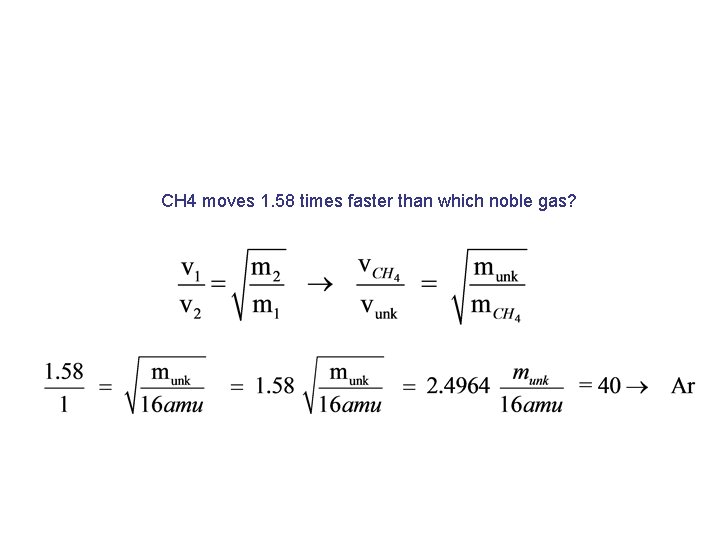
CH 4 moves 1. 58 times faster than which noble gas?

2 17 He Cl 4. 0026 35. 453 Find the relative rate of diffusion of helium and chlorine gas Step 1) Write given information GAS 1 = helium He GAS 2 = chlorine M 1 = 4. 0 g M 2 = 71. 0 g v 1 = x v 2 = x Step 2) Equation Cl 2 Step 3) Substitute into equation and solve v 1 v 2 = 71. 0 g 4. 0 g He diffuses 4. 21 times faster than Cl 2 4. 21 1

The Ideal Gas Idea • All gases expand contract at the same rate (Ideal) • Close to real life (Not Ideal) • Because of this, the densities of gases can be calculated to the point where they would have ZERO volume. – Any guesses at what point this is?

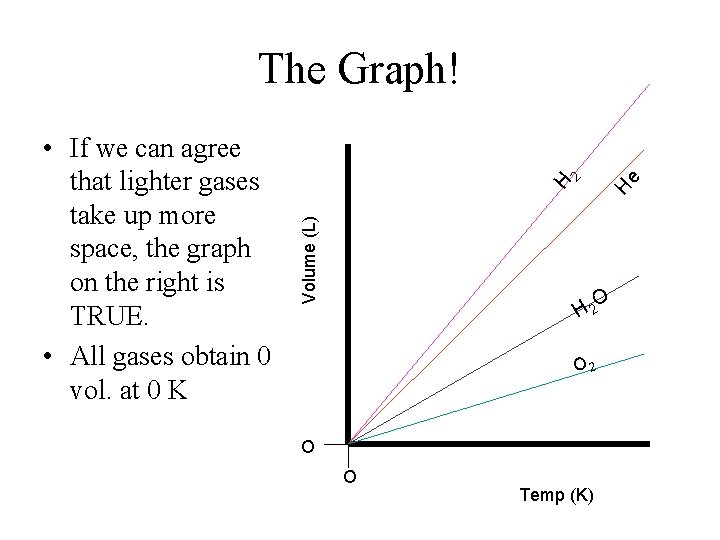
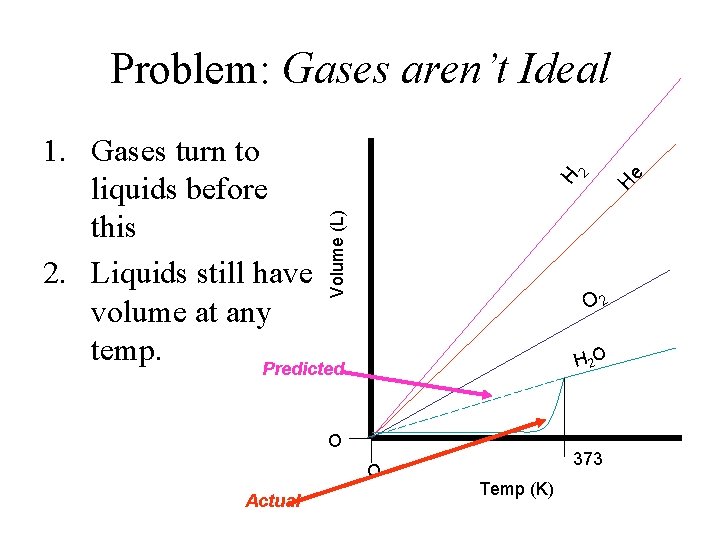
e H H Volume (L) • If we can agree that lighter gases take up more space, the graph on the right is TRUE. • All gases obtain 0 vol. at 0 K 2 The Graph! O H 2 O O Temp (K)

Problem: Gases aren’t Ideal Volume (L) e O 2 H 2 O O O Actual H H 2 1. Gases turn to liquids before this 2. Liquids still have volume at any temp. Predicted 373 Temp (K)

Ideal vs. Real Gases No gas is ideal. Ideal gases remain a gas at any temperature (ignore intermolecular forces). Real gases eventually become a liquid or solid as temperature decreases. Ideal gases DO NOT ACTUALLY EXIST. They are used as a means to simplify the study of gases. Only one of our gas laws deals with REAL gases (treats each gas differently): ___________

Gas Stoichiometry

Gas Stoichiometry Moles Liters of a Gas: – STP - use 22. 4 L/mol – Non-STP - use ideal gas law Non-STP – Given liters of gas? • start with ideal gas law – Looking for liters of gas? • start with stoichiometry conversion Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Stoichiometry Problem What volume of CO 2 forms from 5. 25 g of Ca. CO 3 at 1. 00 atm & 25ºC? Ca. CO 3 5. 25 g Ca. O + Looking for liters: Start with stoich and calculate moles of CO 2. 5. 25 g 1 mol Ca. CO 3 1 mol CO 2 100. 09 g 1 mol Ca. CO 3 CO 2 ? L non-STP = 1. 26 mol CO 2 Plug this into the Ideal Gas Law to find liters. Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Stoichiometry Problem • What volume of CO 2 forms from 5. 25 g of Ca. CO 3 at 1. 00 atm & 25ºC? GIVEN: P = 1. 00 atm V=? n = 1. 26 mol T = 25°C = 298 K R = 0. 0821 L atm/mol K WORK: PV = n. RT (1. 00 atm)V =(1. 26 mol)(0. 0821 L atm/mol K)(298 K) V = 30. 8 L CO 2 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

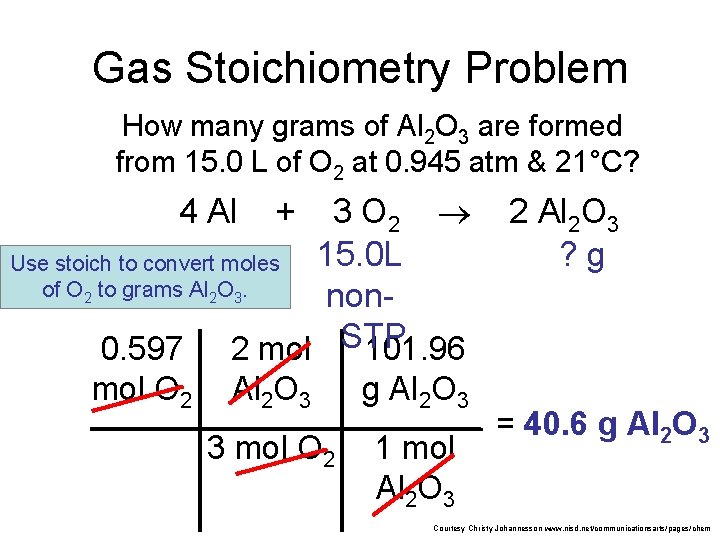
Gas Stoichiometry Problem How many grams of Al 2 O 3 are formed from 15. 0 L O 2 at 0. 945 atm & 21°C? 4 Al + 3 O 2 15. 0 L non. STP of 2 Al 2 O 3 ? g GIVEN: WORK: P = 0. 945 atm V = 15. 0 L n=? T = 21°C = 294 K R = 0. 0821 L atm/mol K PV = n. RT (0. 945 atm) (15. 0 L) = n (0. 0821 L atm/mol K) NEXT (294 K) Given liters: Start with Ideal Gas Law and calculate moles of O 2. n = 0. 597 mol O Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Stoichiometry Problem How many grams of Al 2 O 3 are formed from 15. 0 L of O 2 at 0. 945 atm & 21°C? 3 O 2 15. 0 L Use stoich to convert moles of O 2 to grams Al 2 O 3. non. STP 0. 597 2 mol 101. 96 4 Al mol O 2 + Al 2 O 3 g Al 2 O 3 3 mol O 2 1 mol Al 2 O 3 2 Al 2 O 3 ? g = 40. 6 g Al 2 O 3 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Phase Diagrams (n. and i. ) • New and Improved! • Phase Change Diagrams only account for temperature • New Phase Diagrams account for Pressure, as well. • Terms: – Critical Point – Triple Point *This change comes as a result of our study of Gas Laws!

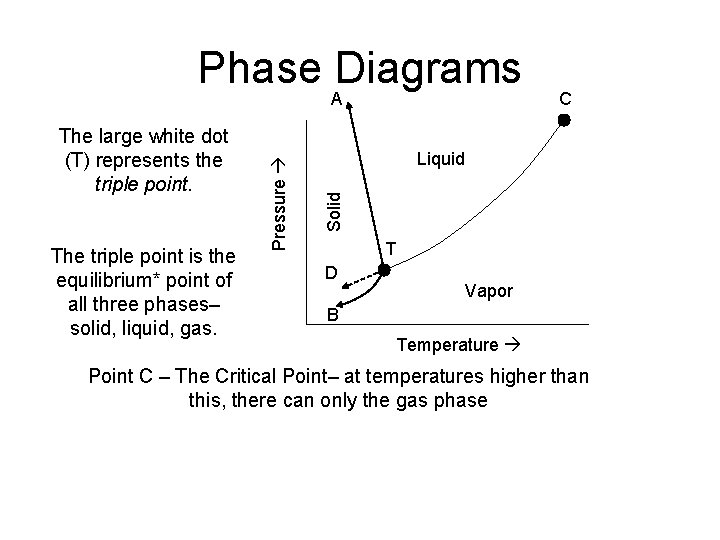
Phase Diagrams The triple point is the equilibrium* point of all three phases– solid, liquid, gas. C Liquid Solid The large white dot (T) represents the triple point. Pressure A T D Vapor B Temperature Point C – The Critical Point– at temperatures higher than this, there can only the gas phase

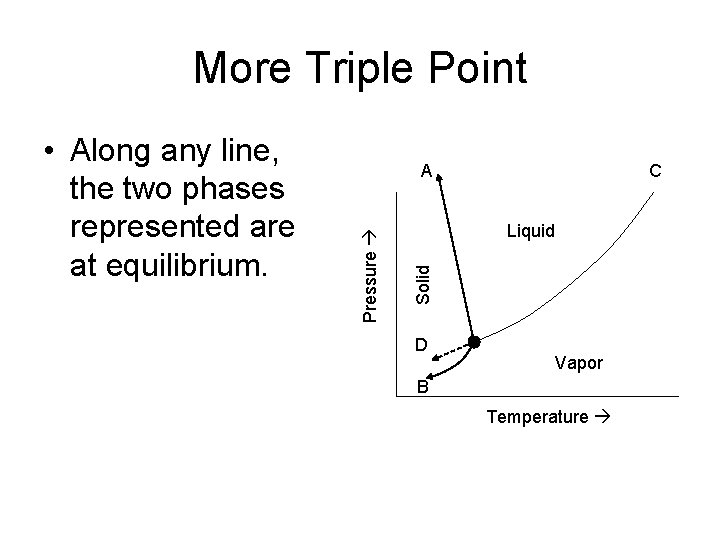
More Triple Point A C Liquid Solid Pressure • Along any line, the two phases represented are at equilibrium. D Vapor B Temperature

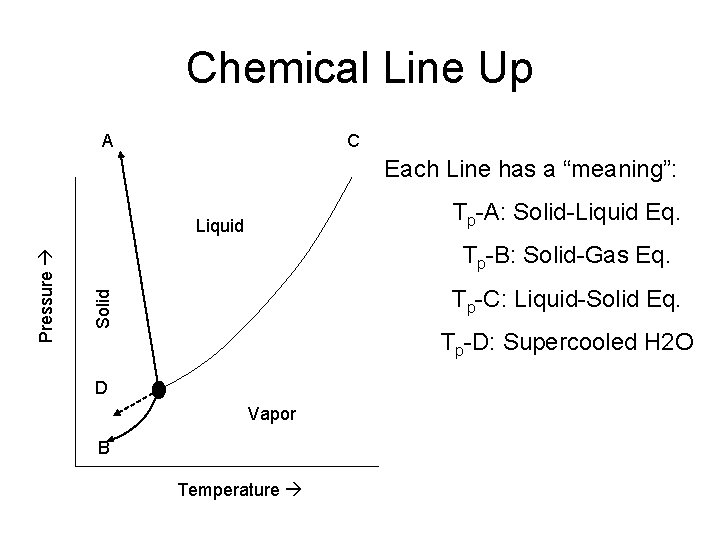
Chemical Line Up A C Each Line has a “meaning”: Tp-A: Solid-Liquid Eq. Tp-B: Solid-Gas Eq. Tp-C: Liquid-Solid Eq. Solid Pressure Liquid Tp-D: Supercooled H 2 O D Vapor B Temperature

Equilibrium • The state in which two or more processes are occurring at the same time: – Phase Changes • As one molecule melts, another freezes • As one molecule boils, another condenses – Triple Point: • ALL of the phase changes occur at the SAME time, at Equilibrium

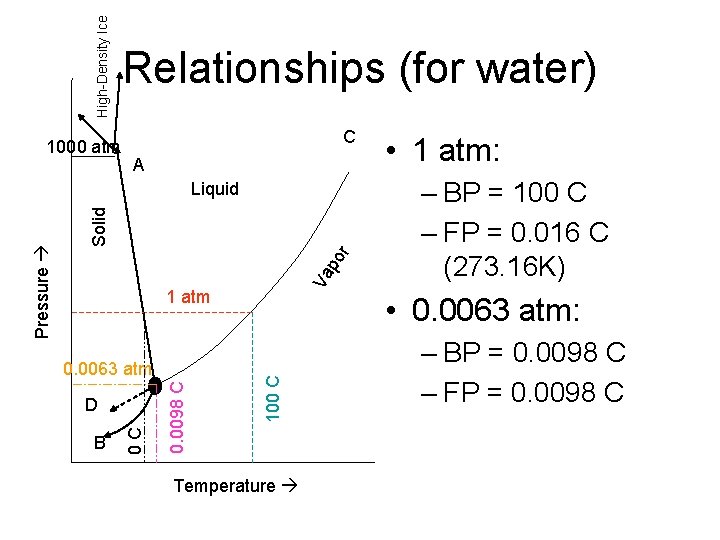
High-Density Ice 1000 atm Relationships (for water) C A Va po r Solid 1 atm B – BP = 100 C – FP = 0. 016 C (273. 16 K) • 0. 0063 atm: 100 C D 0. 0098 C 0. 0063 atm 0 C Pressure Liquid • 1 atm: Temperature – BP = 0. 0098 C – FP = 0. 0098 C

Some Ideas to Consider • Adding pressure causes a shift to the more dense phase. • Adding temp. causes a shift to the less dense phase • “Gibbs Phase Rule”

Water’s Unique Property • What is the most dense phase of water? Gibbs’ Phase Rule explains why ice skates work the way they do!!! The blade of a skate provides pressure to the ice, which should be near 0 C This causes a shift to the more dense phase. This provides a film of water which allows the skate to slide!

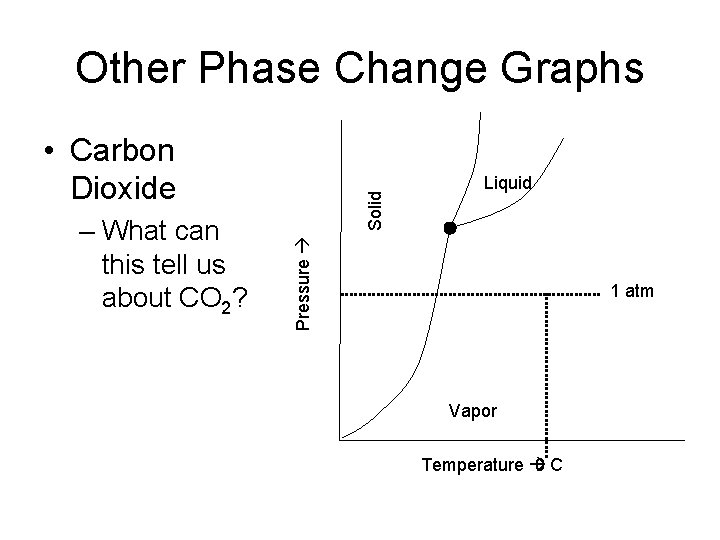
Other Phase Change Graphs Liquid Pressure – What can this tell us about CO 2? Solid • Carbon Dioxide 1 atm Vapor Temperature 0 C

Which Law? • Charles/Boyles/Combined – TWO of: Pressure, Volume, Temperature-- of any one gas • • Ideal: MOLES of ONE gas Grahams: Speed/Velocity/Rate Dalton: PRESSURE of 2 or more gasses Stoich: ONLY 2 chemicals… “How much ____ can you…”