Phase transitions an engineering perspective MASSIMO FRANCESCHETTI University

Phase transitions an engineering perspective MASSIMO FRANCESCHETTI University of California at Berkeley

Phase transition effect when small changes in certain parameters of a system result in dramatic shifts in some globally observed behavior of the system.

Phase transition effect Can we mathematically explain these naturally observed effects?

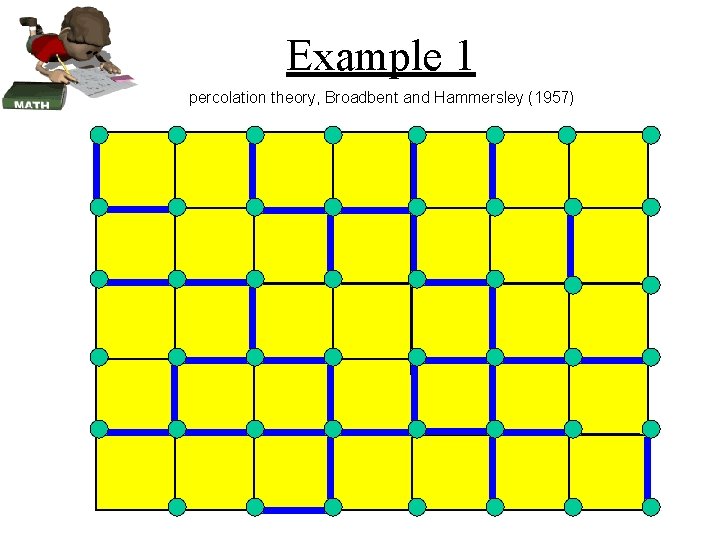
Example 1 percolation theory, Broadbent and Hammersley (1957)

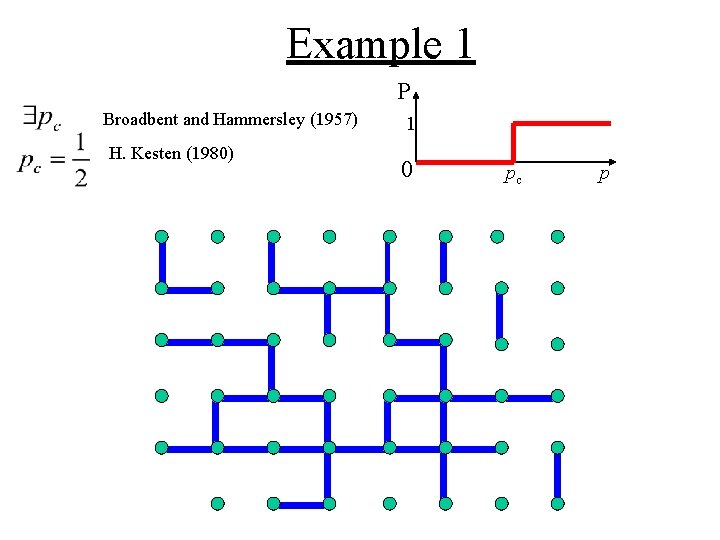
Example 1 P Broadbent and Hammersley (1957) H. Kesten (1980) 1 0 pc p

Example 2 Random graphs, Erdös and Rényi (1959) if graphs with p(n) edges are selected uniformly at random from the set of n-vertex graphs, there is a threshold function, f(n) such that if p(n) < f(n) a randomly chosen graph almost surely has property Q; and if p(n)>f(n), such a graph is very unlikely to have property Q.

Example 3 Continuum percolation, Gilbert (1961) Uniform random distribution of points of density λ One disc per point Studies the formation of an unbounded connected component B A

Example 3 Continuum percolation, Gilbert (1961) The first paper in ad hoc wireless networks ! B A

Example 3 l=0. 4 lc~0. 35910…[Quintanilla, Torquato, Ziff, J. Physics A, 2000]

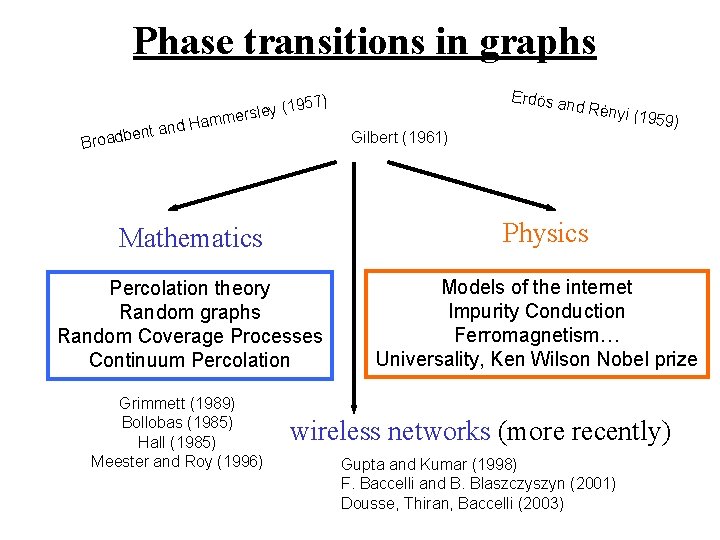
Phase transitions in graphs ent and b d a o r B Erdös a 957) 1 ( y e l s er Hamm Gilbert (1961) yi (1959 ) Physics Mathematics Percolation theory Random graphs Random Coverage Processes Continuum Percolation Grimmett (1989) Bollobas (1985) Hall (1985) Meester and Roy (1996) nd Rén Models of the internet Impurity Conduction Ferromagnetism… Universality, Ken Wilson Nobel prize wireless networks (more recently) Gupta and Kumar (1998) F. Baccelli and B. Blaszczyszyn (2001) Dousse, Thiran, Baccelli (2003)

Not only graphs…

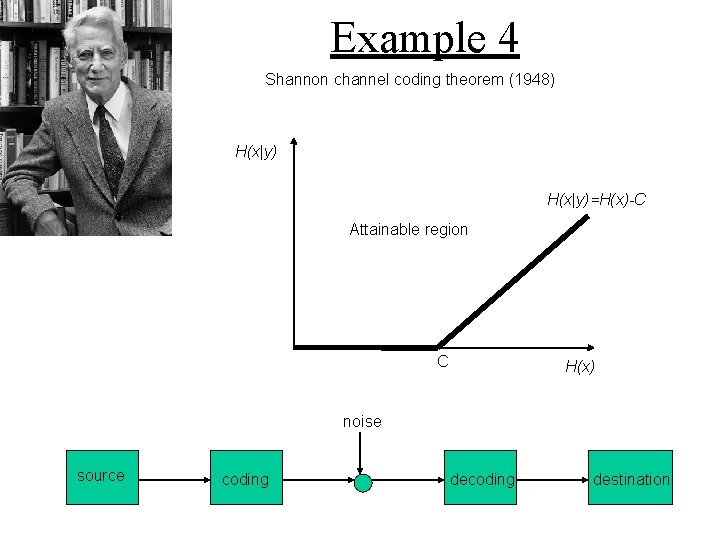
Example 4 Shannon channel coding theorem (1948) H(x|y)=H(x)-C Attainable region C H(x) noise source coding destination

Example 5 “The uncertainty threshold principle, some fundamental limitations of optimal decision making under dynamic uncertainty” Athans, Ku, and Gershwin (1977) xt +1 = g t Axt + d t But + x t yt = xt ì 1 T ü min J = E í å xt 'Q xt + ut ' R ut ý, t = 1, 2. . . ut î T t =0 þ An optimal solution for T ® ¥ exists max | s i ( A) |< 1 / b i

Our contributions to sensor networks Two new percolation models Joint work with L. Booth J. Bruck M. Cook R. Meester Kalman filtering over a lossy network Joint work with B. Sinopoli L. Schenato K. Poolla M. Jordan S. Sastry

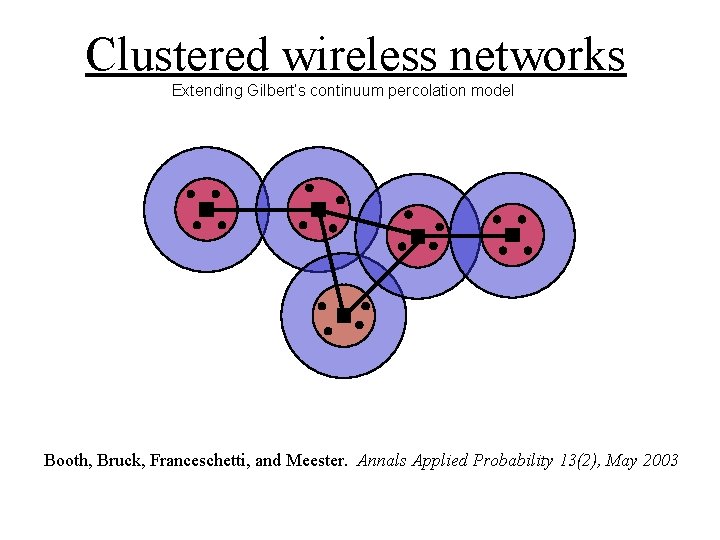
Clustered wireless networks Extending Gilbert’s continuum percolation model Booth, Bruck, Franceschetti, and Meester. Annals Applied Probability 13(2), May 2003

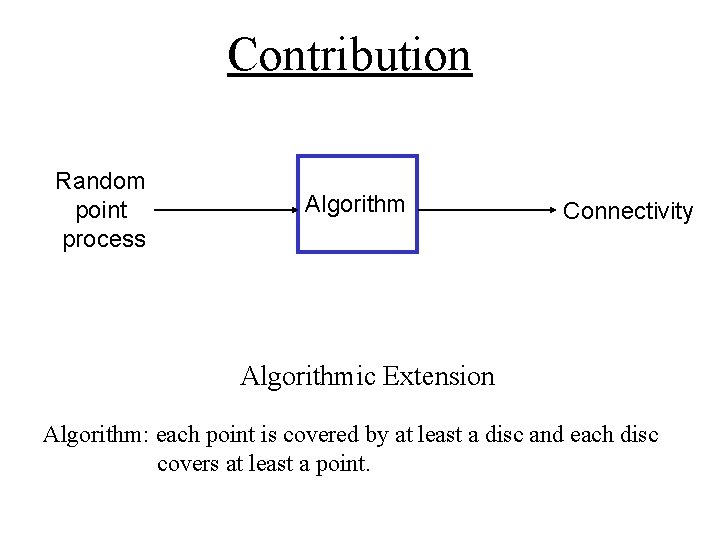
Contribution Random point process Algorithm Connectivity Algorithmic Extension Algorithm: each point is covered by at least a disc and each disc covers at least a point.

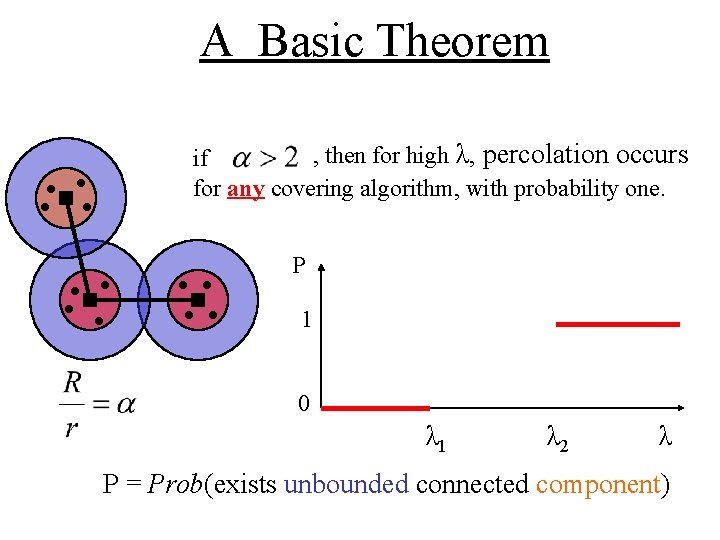
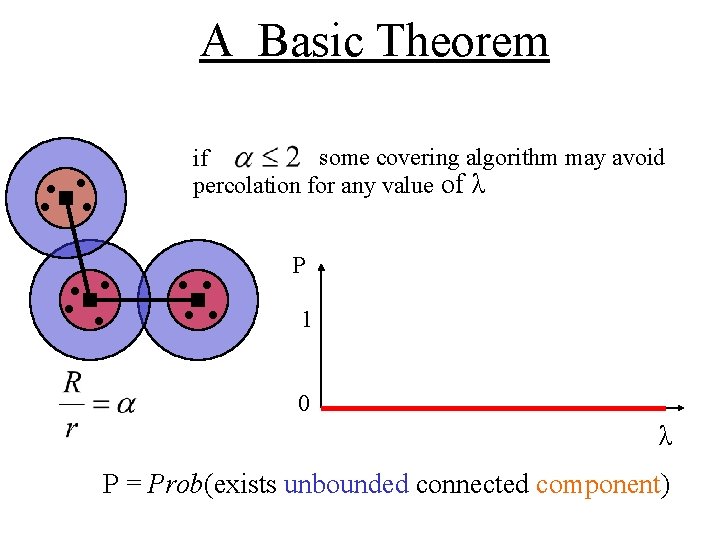
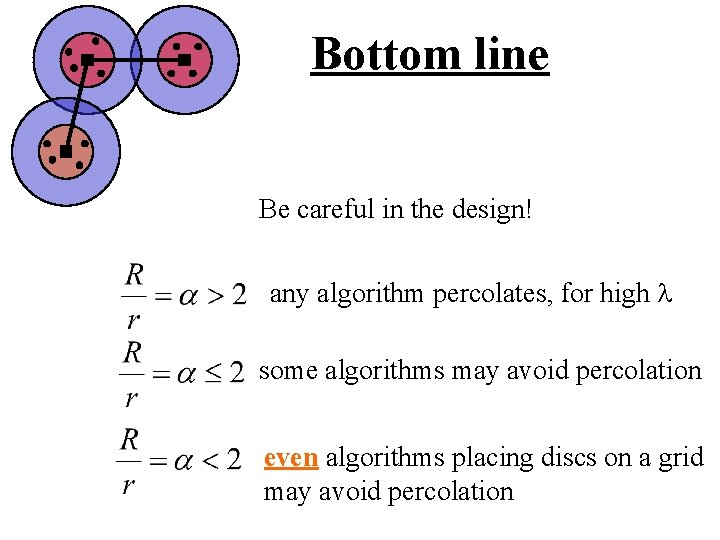
A Basic Theorem , then for high λ, percolation occurs if for any covering algorithm, with probability one. P 1 0 λ 1 λ 2 λ P = Prob(exists unbounded connected component)

A Basic Theorem some covering algorithm may avoid if percolation for any value of λ P 1 0 λ P = Prob(exists unbounded connected component)

Interpretation Note: One disc per point Percolation Gilbert (1961) Need Only Percolation any algorithm

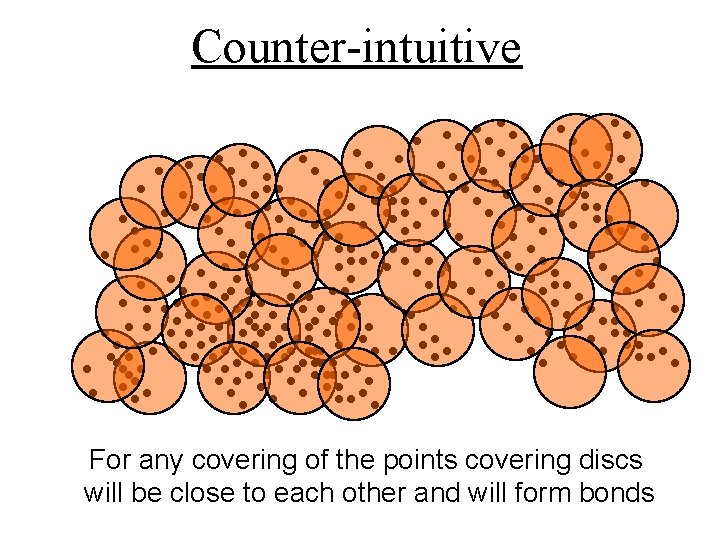
Counter-intuitive For any covering of the points covering discs will be close to each other and will form bonds

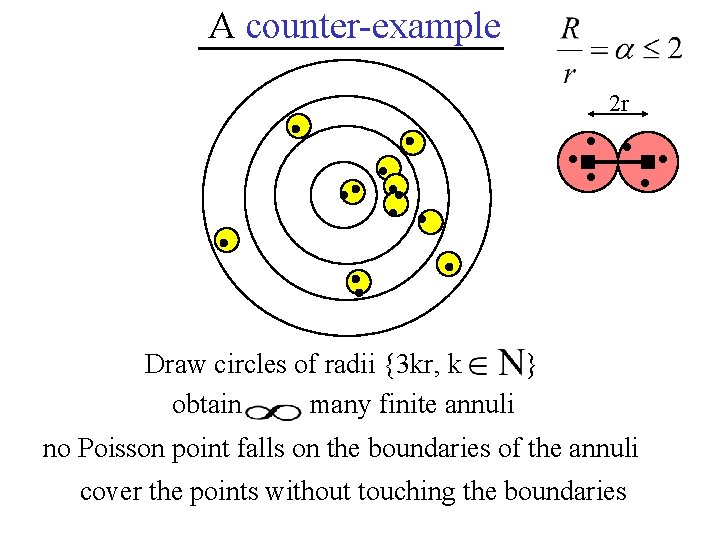
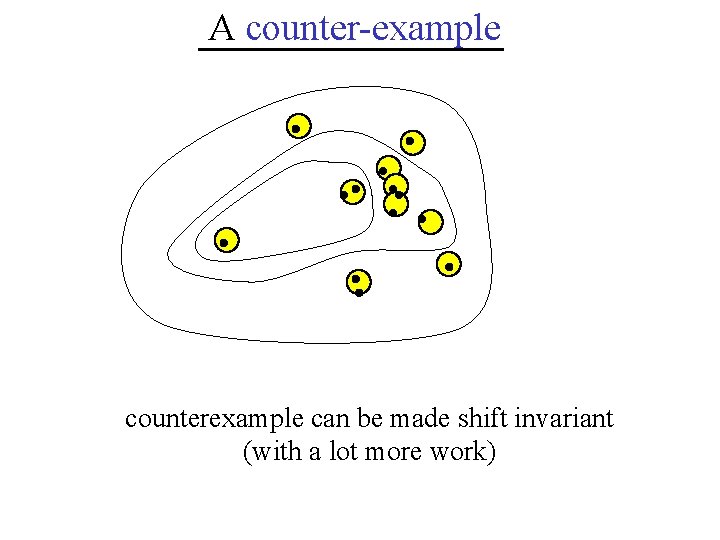
A counter-example 2 r } Draw circles of radii {3 kr, k obtain many finite annuli no Poisson point falls on the boundaries of the annuli cover the points without touching the boundaries

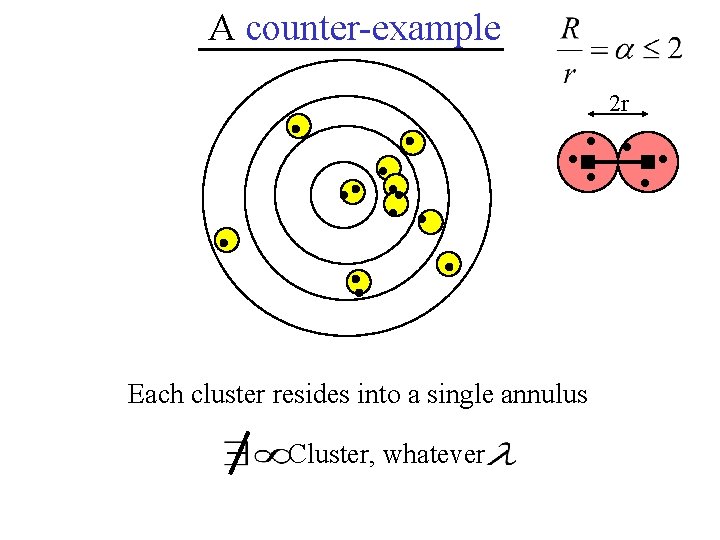
A counter-example 2 r Each cluster resides into a single annulus Cluster, whatever

A counter-example counterexample can be made shift invariant (with a lot more work)

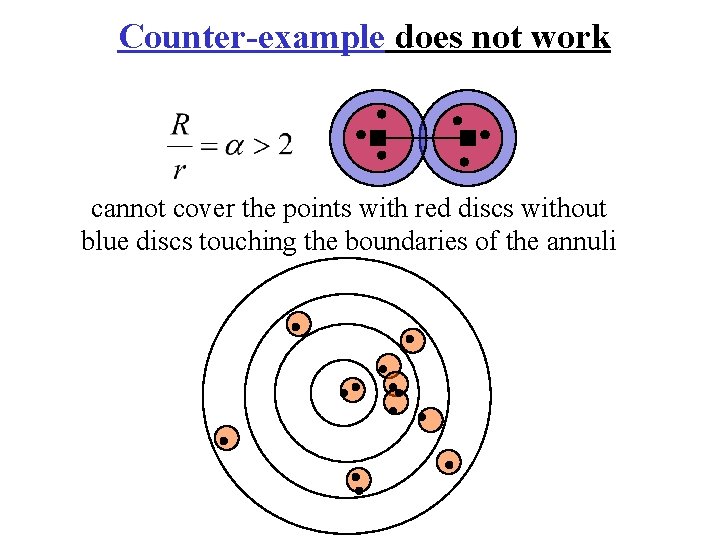
Counter-example does not work cannot cover the points with red discs without blue discs touching the boundaries of the annuli

Proof by lack of counter-example?

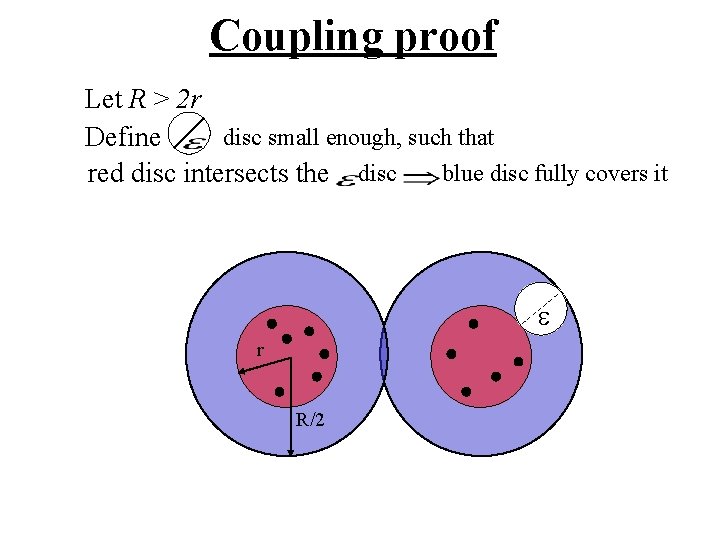
Coupling proof Let R > 2 r disc small enough, such that Define blue disc fully covers it red disc intersects the disc e r R/2

Coupling proof Let R > 2 r disc small enough, such that Define blue disc fully covers it red disc intersects the disc choose l > lc(e), then cover points with red discs

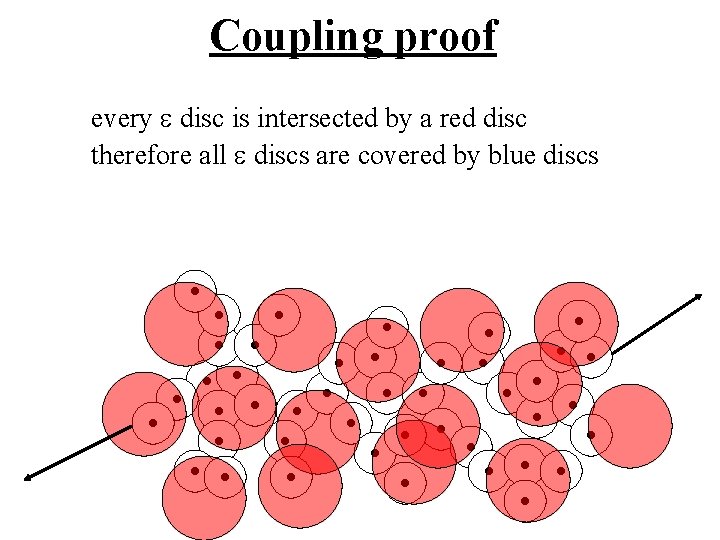
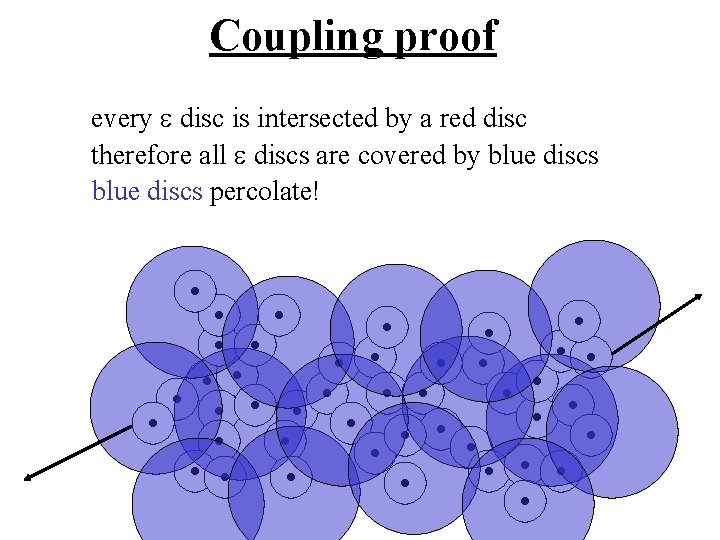
Coupling proof every e disc is intersected by a red disc therefore all e discs are covered by blue discs

Coupling proof every e disc is intersected by a red disc therefore all e discs are covered by blue discs percolate!

Bottom line Be careful in the design! any algorithm percolates, for high l some algorithms may avoid percolation even algorithms placing discs on a grid may avoid percolation

Which classes of algorithms, form an unbounded connected component, a. s. , when is high?

Classes of Algorithms • Grid • Flat • Shift invariant • Finite horizon • Optimal (see paper)

Another extension of percolation Sensor networks with noisy links Franceschetti, Booth, Cook, Bruck, Meester. ISIT ’ 03, July 2003

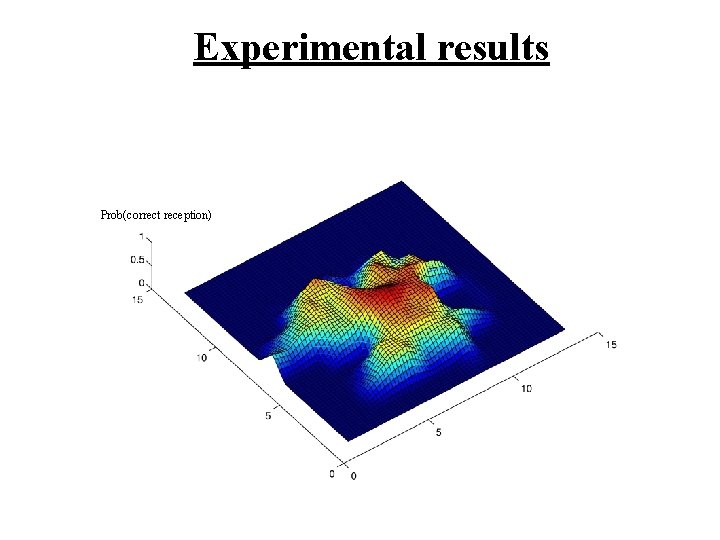
Experiment • 168 rene nodes on a 12 x 14 grid • grid spacing 2 feet • open space • one node transmits “I’m Alive” • surrounding nodes try to receive message http: //localization. millennium. berkeley. edu

Experimental results Prob(correct reception)

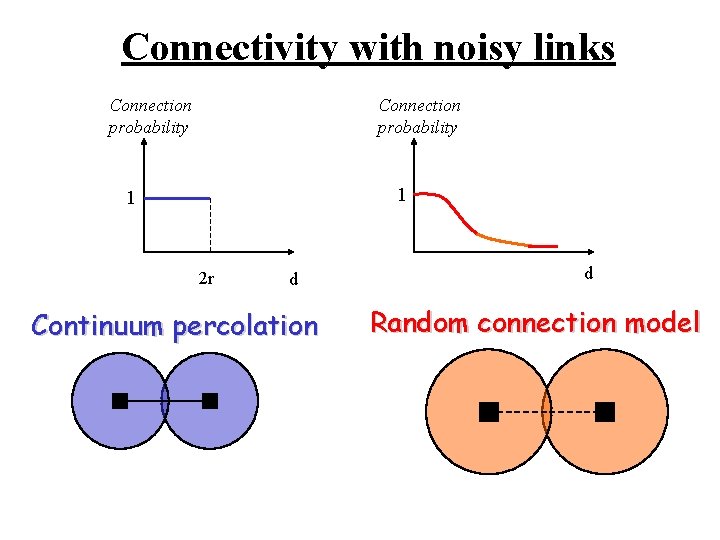
Connectivity with noisy links Connection probability 1 1 2 r d Continuum percolation d Random connection model

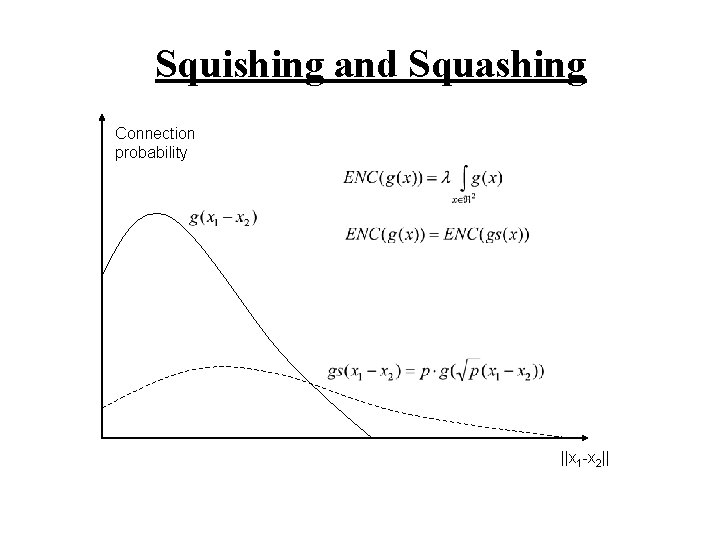
Squishing and Squashing Connection probability ||x 1 -x 2||

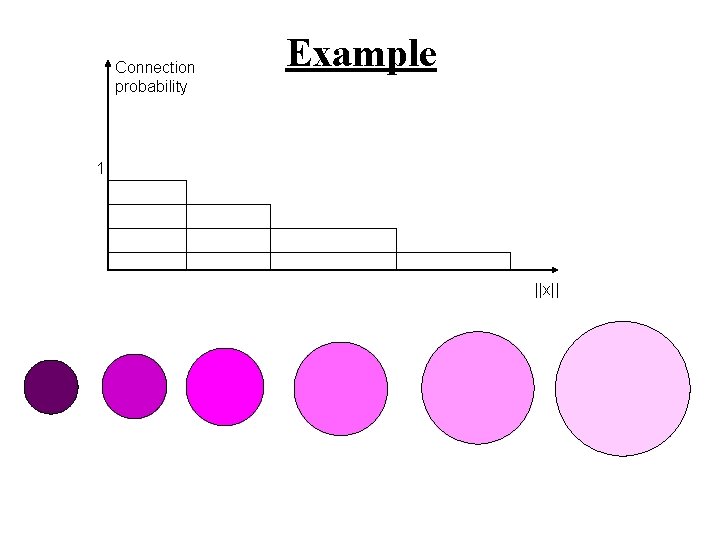
Connection probability Example 1 ||x||

Theorem For all “it is easier to reach connectivity in an unreliable network” “longer links are trading off for the unreliability of the connection”

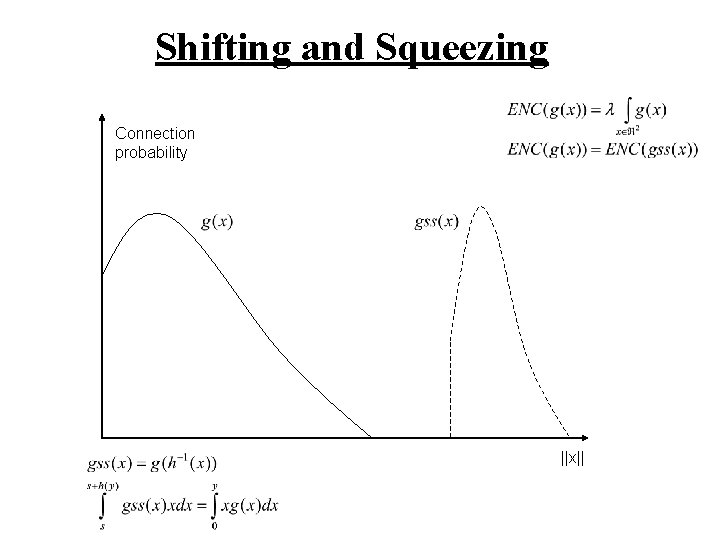
Shifting and Squeezing Connection probability ||x||

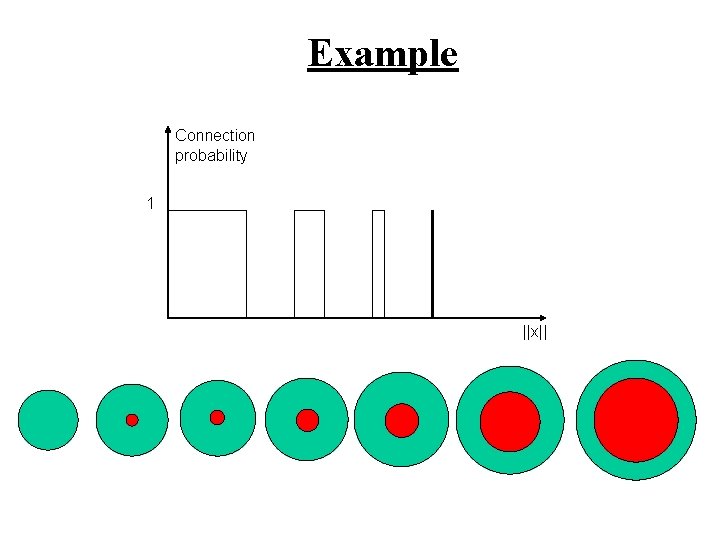
Example Connection probability 1 ||x||

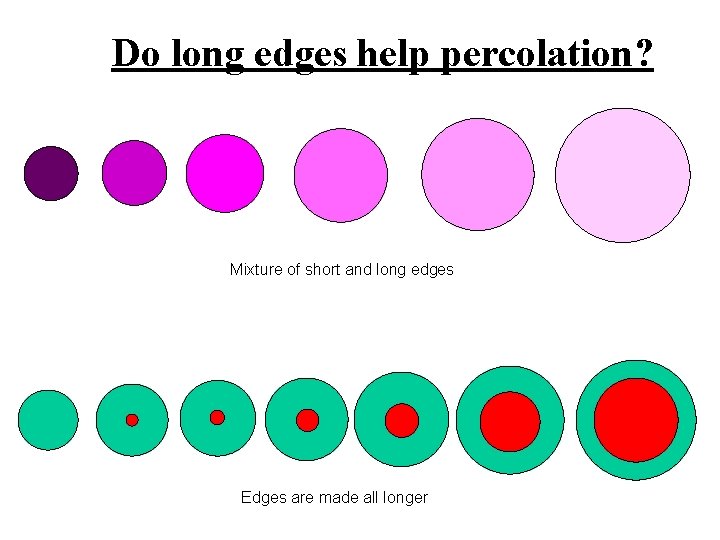
Do long edges help percolation? Mixture of short and long edges Edges are made all longer

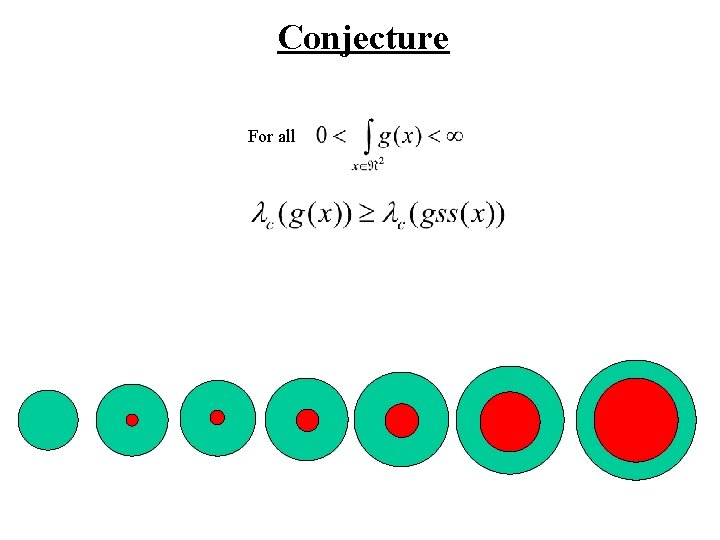
Conjecture For all

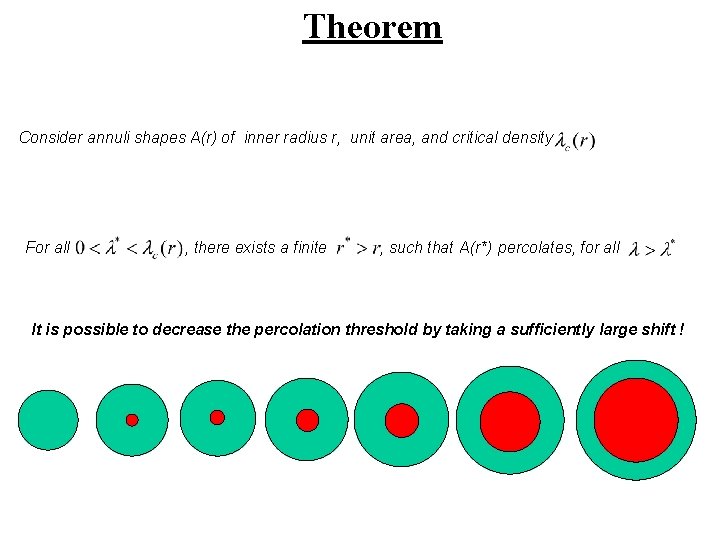
Theorem Consider annuli shapes A(r) of inner radius r, unit area, and critical density For all , there exists a finite , such that A(r*) percolates, for all It is possible to decrease the percolation threshold by taking a sufficiently large shift !

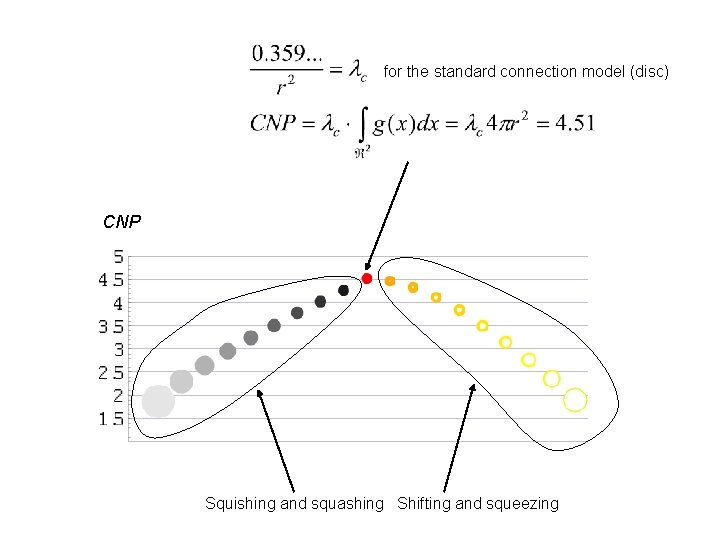
for the standard connection model (disc) CNP Squishing and squashing Shifting and squeezing

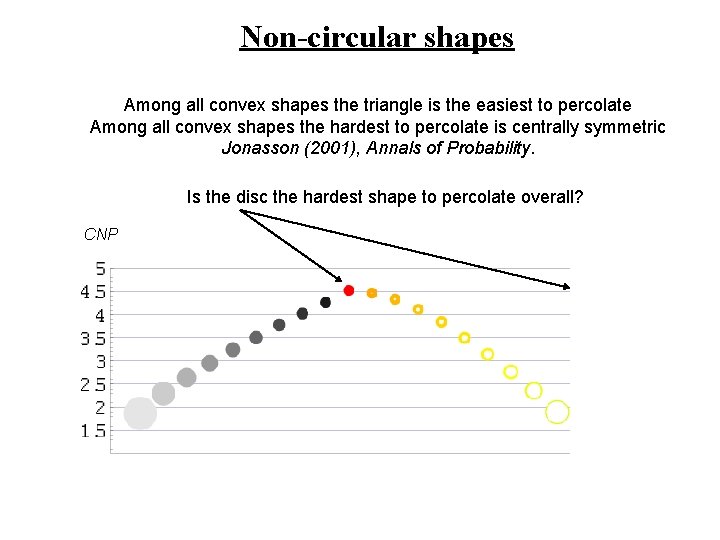
Non-circular shapes Among all convex shapes the triangle is the easiest to percolate Among all convex shapes the hardest to percolate is centrally symmetric Jonasson (2001), Annals of Probability. Is the disc the hardest shape to percolate overall? CNP

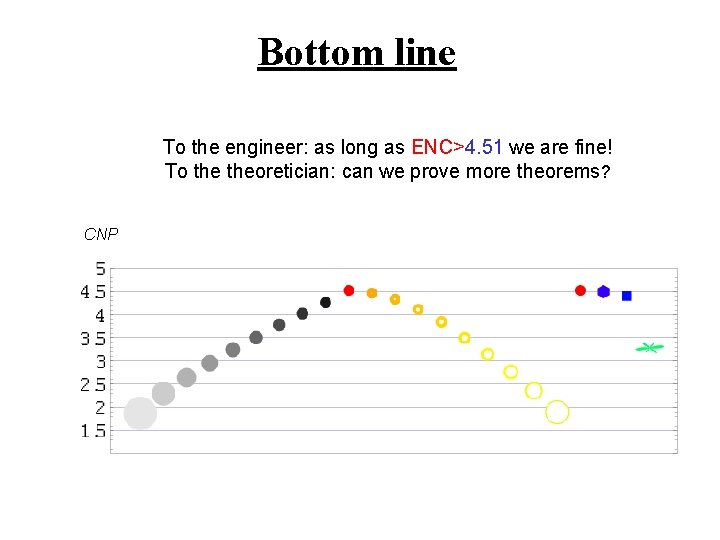
Bottom line To the engineer: as long as ENC>4. 51 we are fine! To theoretician: can we prove more theorems? CNP