Phase space moment equation model of highly relativistic

Phase space moment equation model of highly relativistic electron beams in plasma wakefield accelerators Robert Robson 1, Timon Mehrling 2, Jan-Hendrik Erbe 2 and Jens Osterhoff 2 1. School of Natural Sciences, Griffith University, Brisbane, Australia 2. Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany r. robson@griffith. edu. au

What this talk is about 1. A new theoretical technique for rapid, accurate calculation of average phase space properties of an electron beam injected into & extracted from a laser wakefield 2. At first plasma properties are assumed uniform (benchmark model) 3. Generalize the procedure to realistic profiles quick, accurate alternative to PIC 2

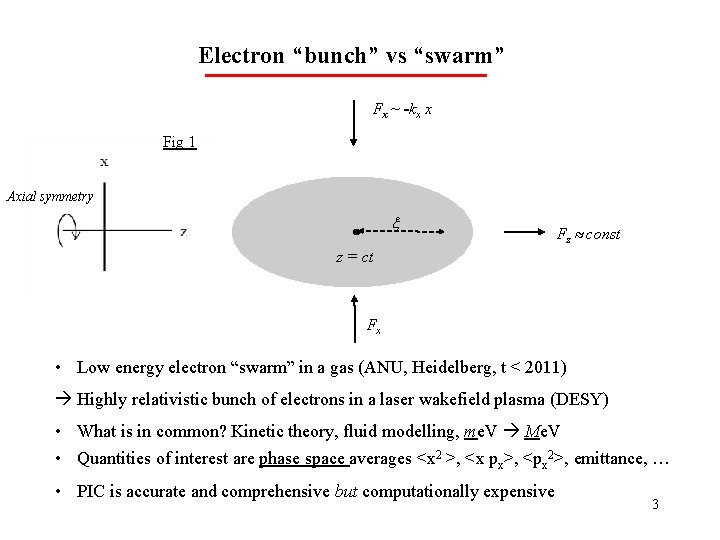
Electron “bunch” vs “swarm” Fx ~ -kx x Fig 1 Axial symmetry Fz const z = ct Fx • Low energy electron “swarm” in a gas (ANU, Heidelberg, t < 2011) Highly relativistic bunch of electrons in a laser wakefield plasma (DESY) • What is in common? Kinetic theory, fluid modelling, me. V Me. V • Quantities of interest are phase space averages <x 2 >, <x px>, <px 2>, emittance, … • PIC is accurate and comprehensive but computationally expensive 3

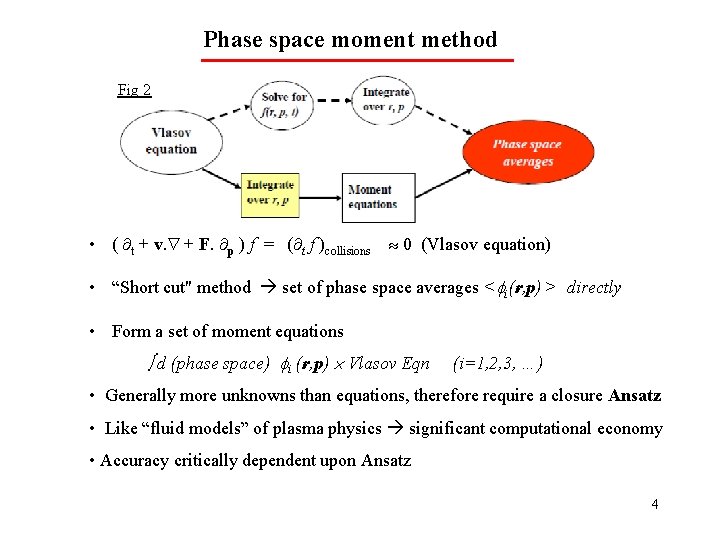
Phase space moment method Fig 2 • ( t + v. + F. p ) f = ( t f )collisions 0 (Vlasov equation) • “Short cut" method set of phase space averages < i(r, p) > directly • Form a set of moment equations d (phase space) i (r, p) Vlasov Eqn (i=1, 2, 3, …) • Generally more unknowns than equations, therefore require a closure Ansatz • Like “fluid models” of plasma physics significant computational economy • Accuracy critically dependent upon Ansatz 4

Basic moment equations 5

Benchmark model – analytic solution 6

Semi-analytical numerical analysis (SANA) 7

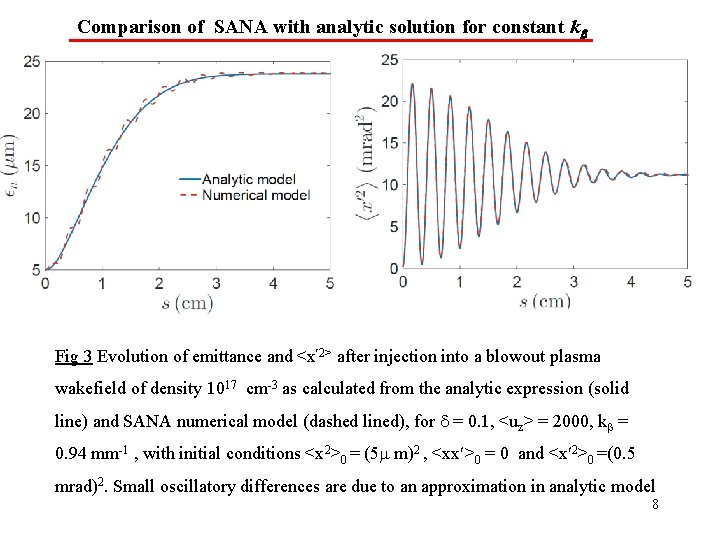
Comparison of SANA with analytic solution for constant k Fig 3 Evolution of emittance and <x 2> after injection into a blowout plasma wakefield of density 1017 cm-3 as calculated from the analytic expression (solid line) and SANA numerical model (dashed lined), for = 0. 1, <uz> = 2000, k = 0. 94 mm-1 , with initial conditions <x 2>0 = (5 m)2 , <xx >0 = 0 and <x 2>0 =(0. 5 mrad)2. Small oscillatory differences are due to an approximation in analytic model 8

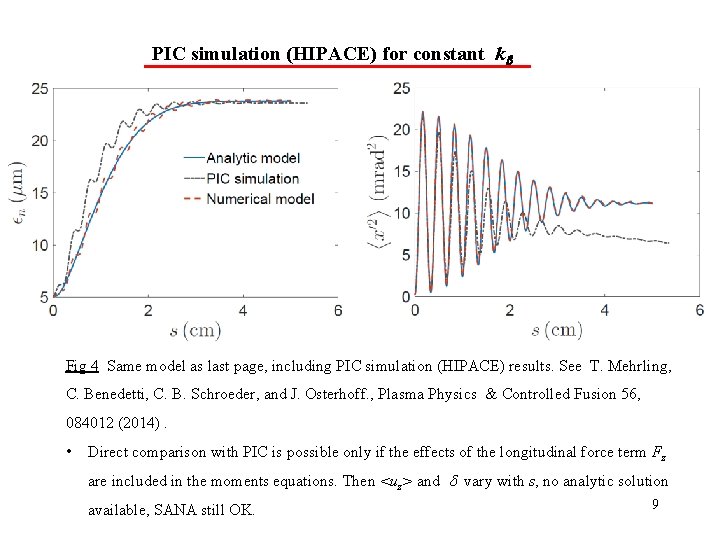
PIC simulation (HIPACE) for constant k Fig 4 Same model as last page, including PIC simulation (HIPACE) results. See T. Mehrling, C. Benedetti, C. B. Schroeder, and J. Osterhoff. , Plasma Physics & Controlled Fusion 56, 084012 (2014). • Direct comparison with PIC is possible only if the effects of the longitudinal force term Fz are included in the moments equations. Then <uz> and vary with s, no analytic solution available, SANA still OK. 9

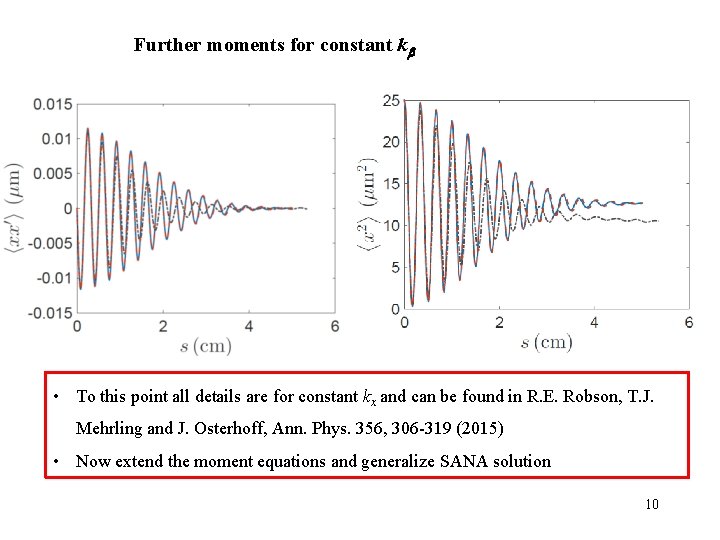
Further moments for constant k • To this point all details are for constant kx and can be found in R. E. Robson, T. J. Mehrling and J. Osterhoff, Ann. Phys. 356, 306 -319 (2015) • Now extend the moment equations and generalize SANA solution 10

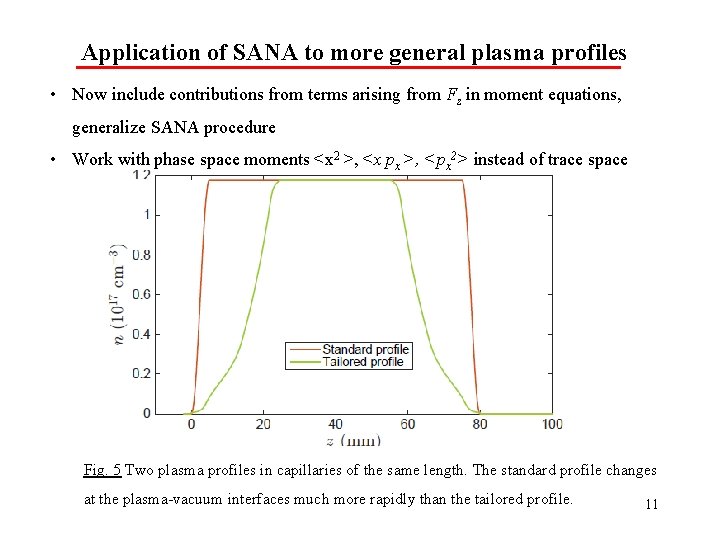
Application of SANA to more general plasma profiles • Now include contributions from terms arising from Fz in moment equations, generalize SANA procedure • Work with phase space moments <x 2 >, <x px >, <px 2> instead of trace space Fig. 5 Two plasma profiles in capillaries of the same length. The standard profile changes at the plasma-vacuum interfaces much more rapidly than the tailored profile. 11

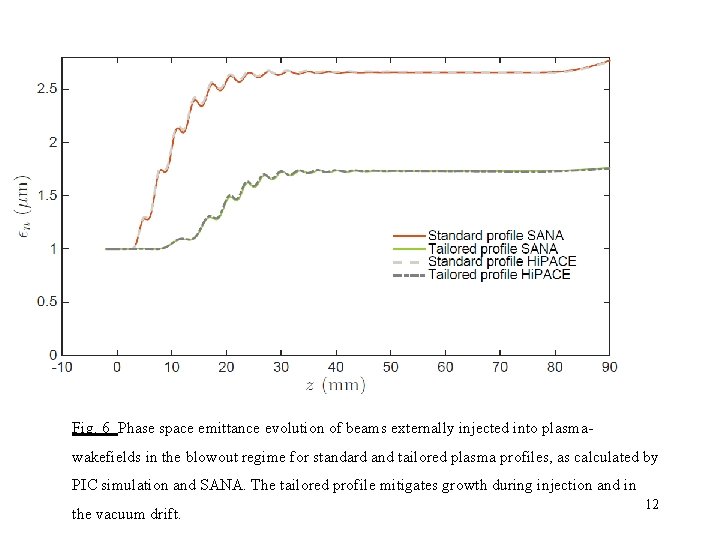
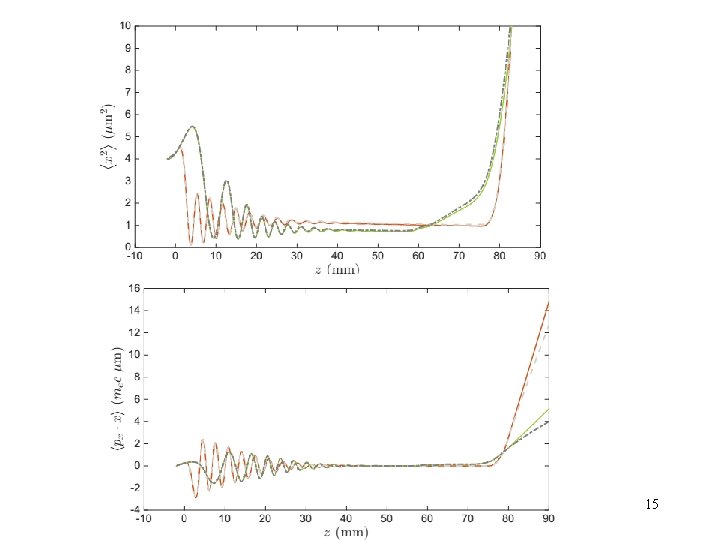
Fig. 6 Phase space emittance evolution of beams externally injected into plasmawakefields in the blowout regime for standard and tailored plasma profiles, as calculated by PIC simulation and SANA. The tailored profile mitigates growth during injection and in the vacuum drift. 12

SUMMARY • Vlasov kinetic equation equivalent set of phase-space moment equations, closure achieved through an Ansatz • An analytic solution has been obtained for constant betatron wavenumber, for use as a benchmark • An analytic/numerical procedure (SANA) has been developed for arbitrary plasma density profiles and betatron wavenumbers • SANA - compares well with PIC simulations + computationally economical - quickly calculates emittance growth during injection/ extraction phases - enables rapid optimization of plasma target density profiles - this is the key to generation of high quality beams in plasma-based acceleration 13

References R. E. Robson, T. J. Mehrling and J. Osterhoff, Ann. Phys. 356, 306 -319 (2015) [Methodology & details] T. Mehrling , C. Benedetti, C. B. Schroeder, and J. Osterhoff. , Plasma Physics & Controlled Fusion 56, 084012 (2014) [HIPACE PIC simulation details] R. E. Robson, et al, Rev. Mod. Phys 77, 1303 -20 (2005) [Fluid analysis in configuration space] K. Kumar, J. Phys. D 14, 2199 (1981) [ Phase space moment method for low energy electrons] THANK YOU FOR YOUR Isola d’Elba ATTENTION! Isola di Coochiemudlo 1. 6 104 km 14

15