Phase Diagrams Shows the states of matter that




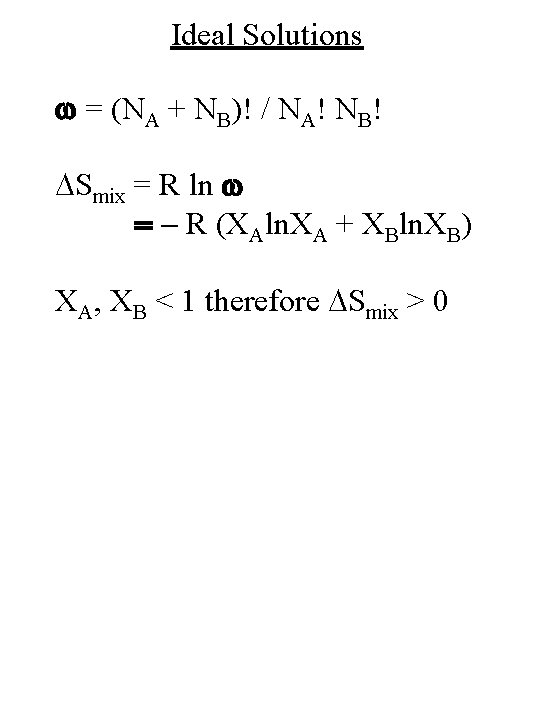





- Slides: 33

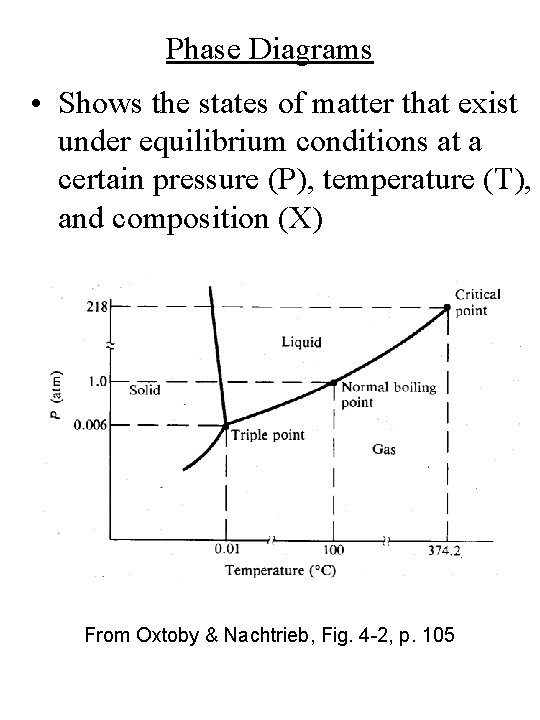
Phase Diagrams • Shows the states of matter that exist under equilibrium conditions at a certain pressure (P), temperature (T), and composition (X) From Oxtoby & Nachtrieb, Fig. 4 -2, p. 105

Phase Diagrams States of matter : • Solid • Liquid • Gas • Different crystalline forms • e. g. , Ga has orthorhombic crystal structure (g) • As has rhombohedral crystal structure (a) • Ga 0. 5 As 0. 5 has zincblende crystal structure (c)

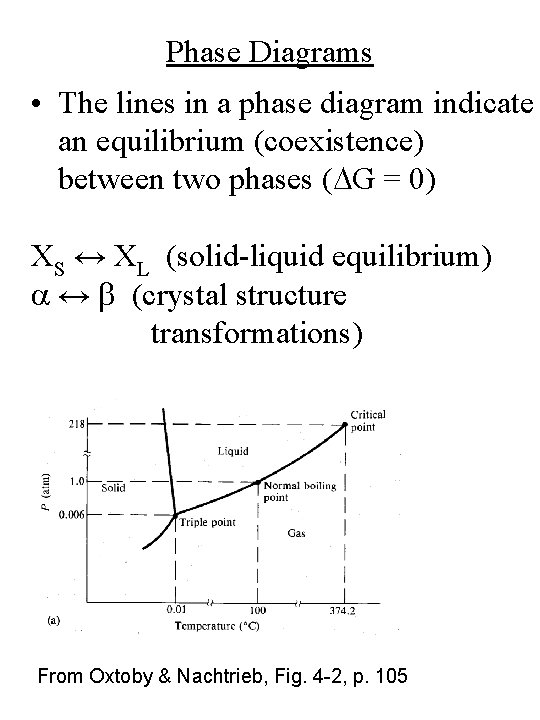
Phase Diagrams • The lines in a phase diagram indicate an equilibrium (coexistence) between two phases (DG = 0) XS ↔ XL (solid-liquid equilibrium) a ↔ b (crystal structure transformations) From Oxtoby & Nachtrieb, Fig. 4 -2, p. 105

Two-Component Phase Diagrams • One-component phase diagram is a 2 -D plot of T (x-axis) versus P (yaxis) • For two components, phase diagram is a 3 -D plot of T, P, and X; usually plot X (x-axis) versus T (y-axis) with P fixed • Caution: P for phase diagrams is usually fixed at 1 atm (STP); but MBE occurs a lower pressures (< 10 -3 Torr)

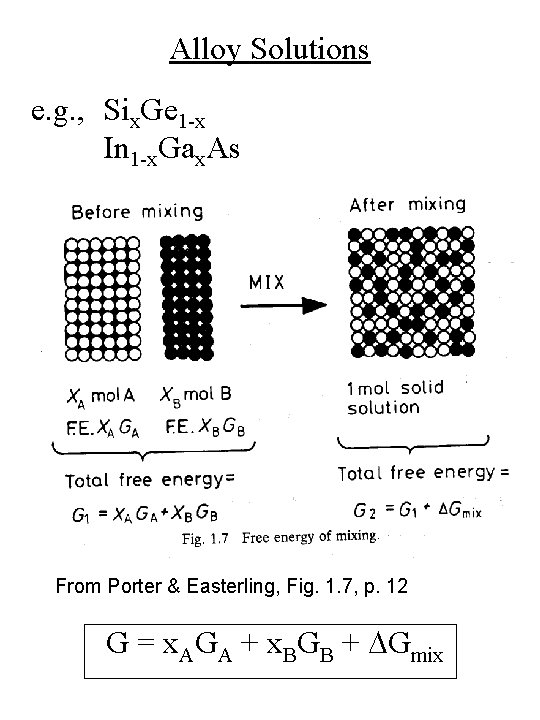
Alloy Solutions e. g. , Six. Ge 1 -x In 1 -x. Gax. As From Porter & Easterling, Fig. 1. 7, p. 12 G = x. AGA + x. BGB + DGmix

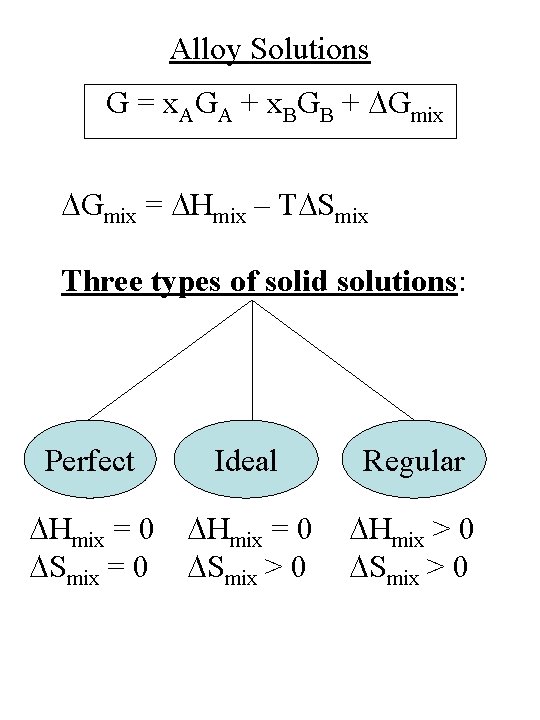
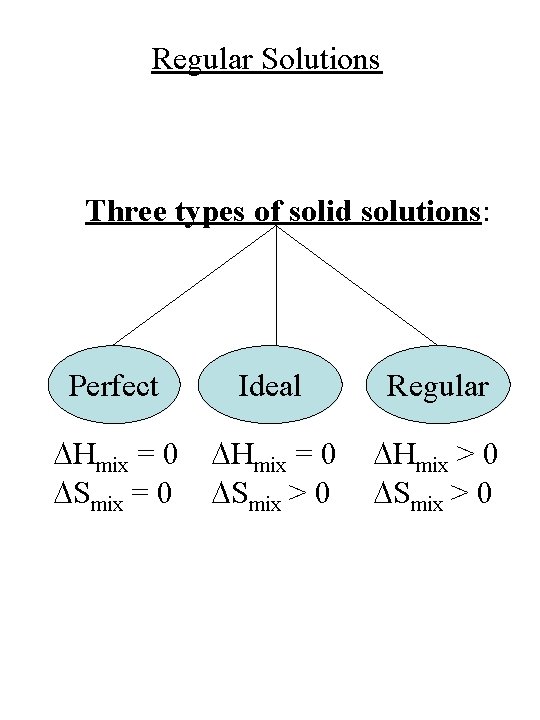
Alloy Solutions G = x. AGA + x. BGB + DGmix = DHmix – TDSmix Three types of solid solutions: Perfect Ideal Regular DHmix = 0 DSmix = 0 DHmix = 0 DSmix > 0 DHmix > 0 DSmix > 0

Perfect Solutions G = x. AGA + x. BGB • DHmix = 0 • DSmix = 0 • e. g. , a gas mixture where atoms do not interact (ideal gas) From Porter & Easterling, Fig. 1. 8, p. 13

Ideal Solutions • Atoms are chemically similar and occupy similar lattice sites, e. g. , Six. Ge 1 -x (DHmix ~ 0) • Boltzmann equation: DSmix = R ln w (configurational entropy) w = # distinguishable ways of arranging atoms in the solution From Porter & Easterling, Fig. 1. 7, p. 12
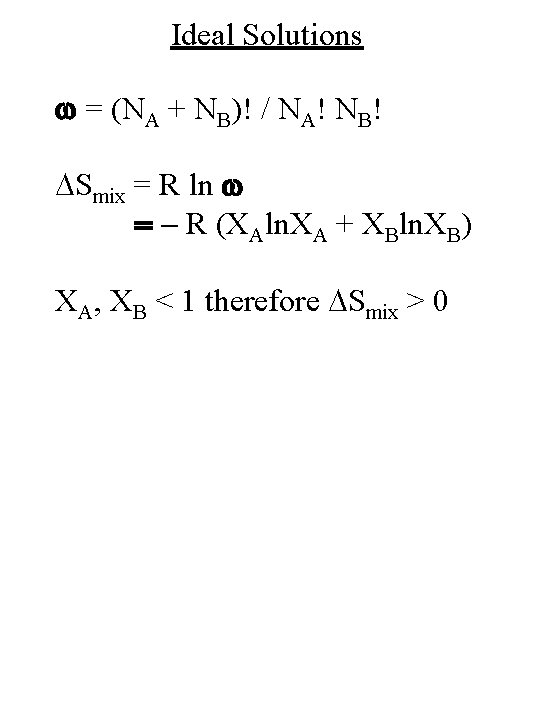
Ideal Solutions w = (NA + NB)! / NA! NB! DSmix = R ln w = - R (XAln. XA + XBln. XB) XA, XB < 1 therefore DSmix > 0

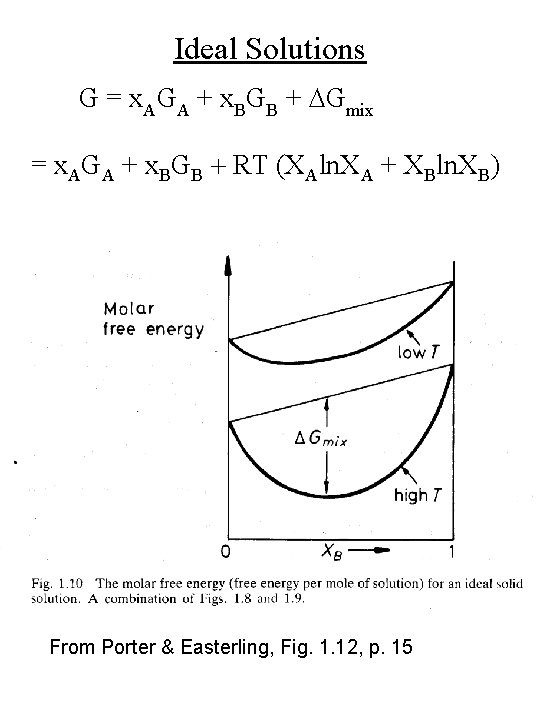
Ideal Solutions G = x. AGA + x. BGB + DGmix = x. AGA + x. BGB + RT (XAln. XA + XBln. XB) From Porter & Easterling, Fig. 1. 12, p. 15

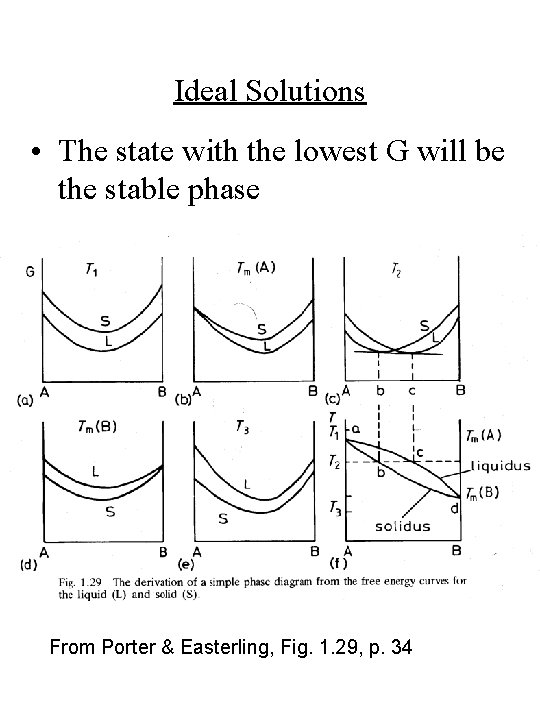
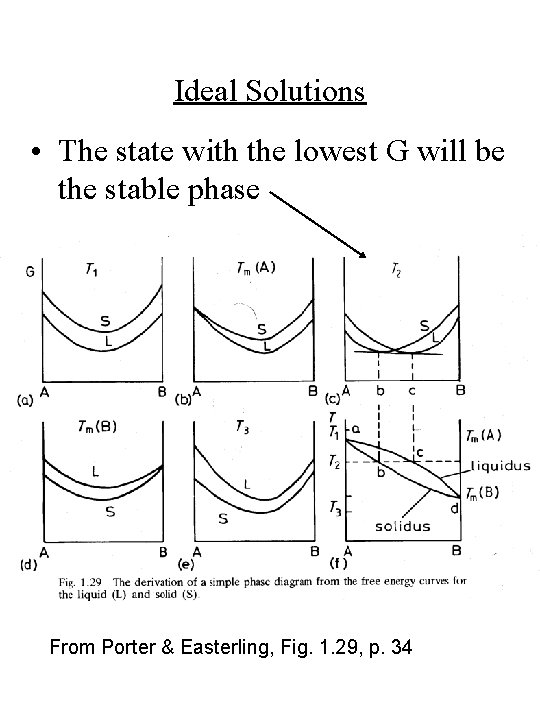
Ideal Solutions • The state with the lowest G will be the stable phase From Porter & Easterling, Fig. 1. 29, p. 34

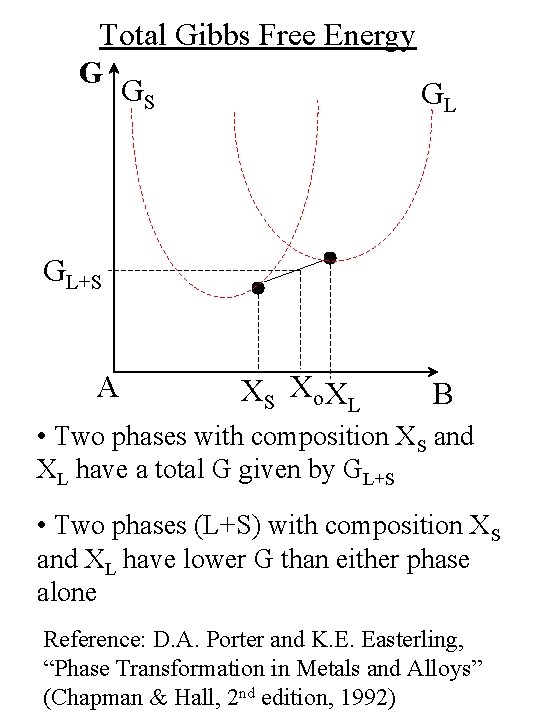
Total Gibbs Free Energy G GS GL GL+S A XS Xo XL B • Two phases with composition XS and XL have a total G given by GL+S • Two phases (L+S) with composition XS and XL have lower G than either phase alone Reference: D. A. Porter and K. E. Easterling, “Phase Transformation in Metals and Alloys” (Chapman & Hall, 2 nd edition, 1992)

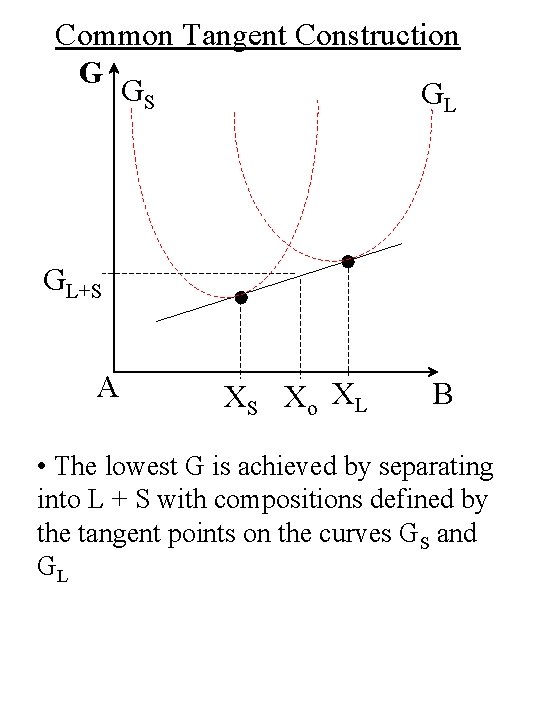
Common Tangent Construction G GS GL GL+S A XS Xo XL B • The lowest G is achieved by separating into L + S with compositions defined by the tangent points on the curves GS and GL

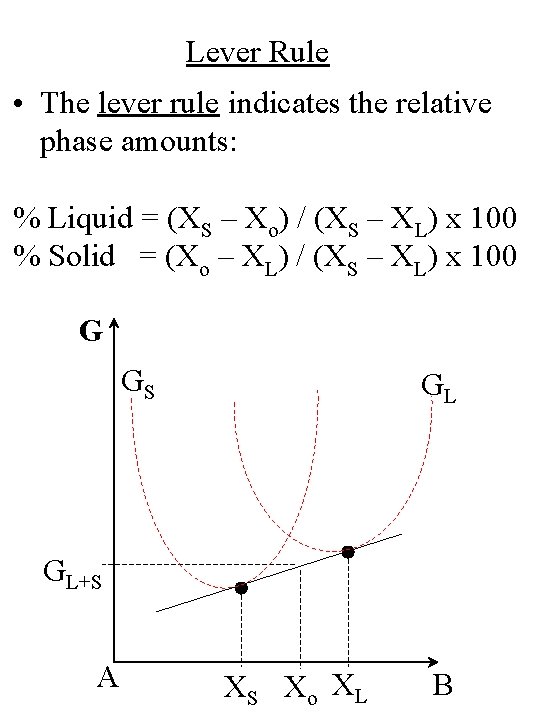
Lever Rule • The lever rule indicates the relative phase amounts: % Liquid = (XS – Xo) / (XS – XL) x 100 % Solid = (Xo – XL) / (XS – XL) x 100 G GS GL GL+S A XS Xo XL B

Ideal Solutions • The state with the lowest G will be the stable phase From Porter & Easterling, Fig. 1. 29, p. 34

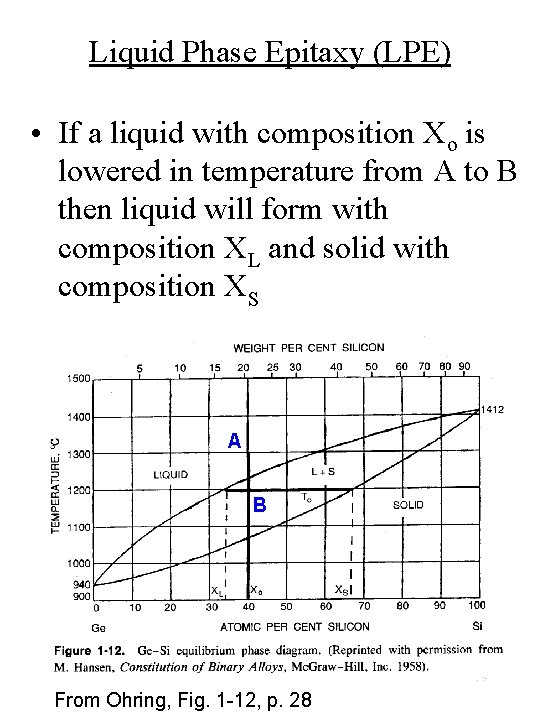
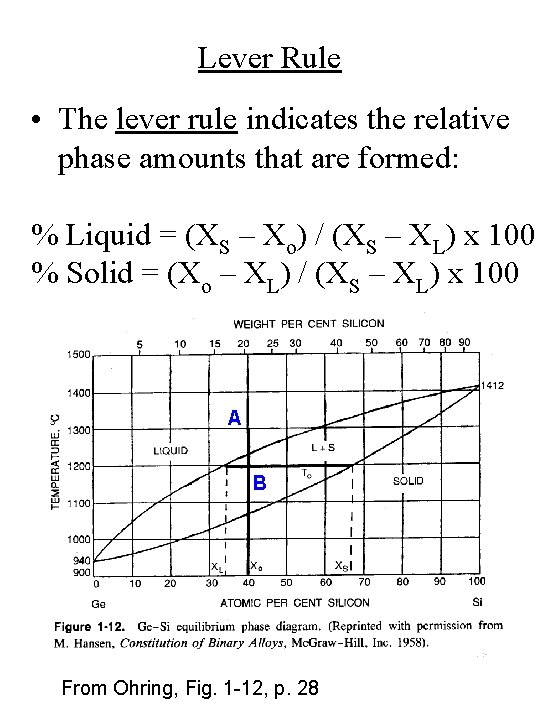
Liquid Phase Epitaxy (LPE) • If a liquid with composition Xo is lowered in temperature from A to B then liquid will form with composition XL and solid with composition XS A B From Ohring, Fig. 1 -12, p. 28

Lever Rule • The lever rule indicates the relative phase amounts that are formed: % Liquid = (XS – Xo) / (XS – XL) x 100 % Solid = (Xo – XL) / (XS – XL) x 100 A B From Ohring, Fig. 1 -12, p. 28

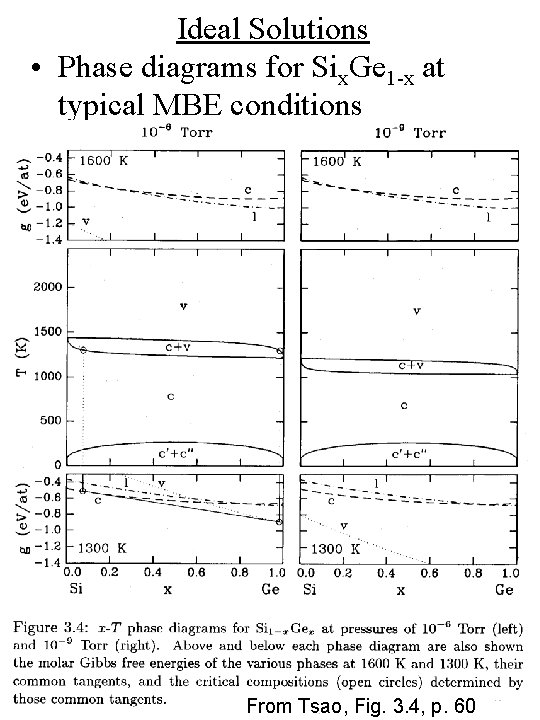
Ideal Solutions • Phase diagrams for Six. Ge 1 -x at typical MBE conditions From Tsao, Fig. 3. 4, p. 60

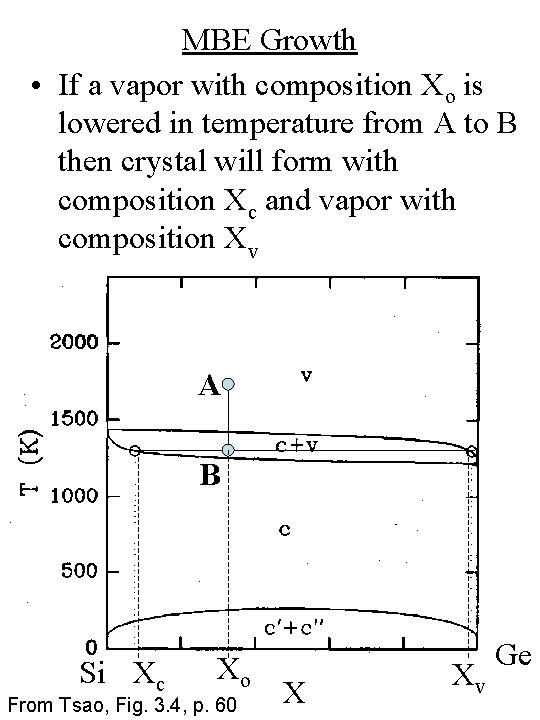
MBE Growth • If a vapor with composition Xo is lowered in temperature from A to B then crystal will form with composition Xc and vapor with composition Xv A B Si Xc Xo From Tsao, Fig. 3. 4, p. 60 X Xv Ge

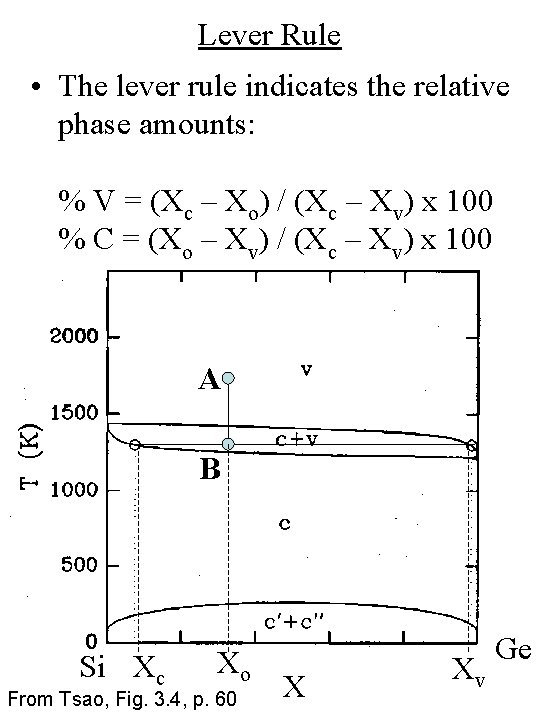
Lever Rule • The lever rule indicates the relative phase amounts: % V = (Xc – Xo) / (Xc – Xv) x 100 % C = (Xo – Xv) / (Xc – Xv) x 100 A B Si Xc Xo From Tsao, Fig. 3. 4, p. 60 X Xv Ge

Regular Solutions Three types of solid solutions: Perfect Ideal Regular DHmix = 0 DSmix = 0 DHmix = 0 DSmix > 0 DHmix > 0 DSmix > 0

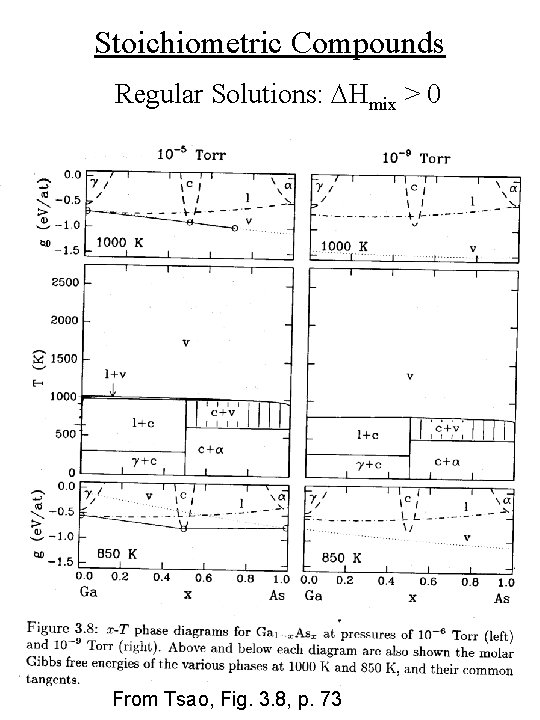
Regular Solutions e. g. , Stoichiometric Compounds • e. g. , Ga + As Ga. As • Ga has orthorhombic crystal structure (g) • As has rhombohedral crystal structure (a) • Ga 0. 5 As 0. 5 has zincblende crystal structure (c) • 7 phases: solid Ga, solid As, solid Ga. As, liquid Ga, vapor As 2

Stoichiometric Compounds Regular Solutions: DHmix > 0 From Tsao, Fig. 3. 8, p. 73

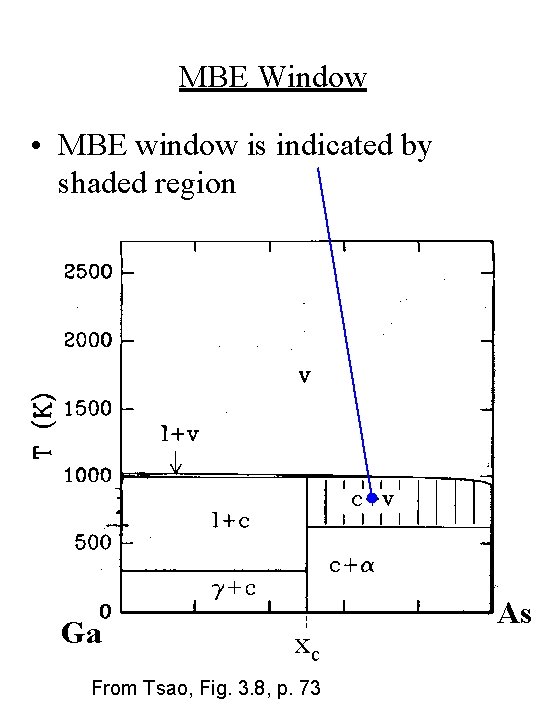
MBE Window • MBE window is indicated by shaded region Ga xc From Tsao, Fig. 3. 8, p. 73 As

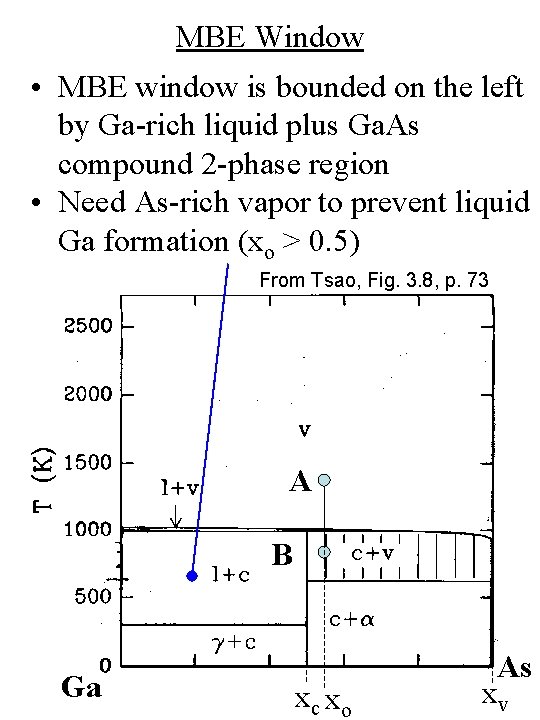
MBE Window • MBE window is bounded on the left by Ga-rich liquid plus Ga. As compound 2 -phase region • Need As-rich vapor to prevent liquid Ga formation (xo > 0. 5) From Tsao, Fig. 3. 8, p. 73 A B Ga xc xo As xv

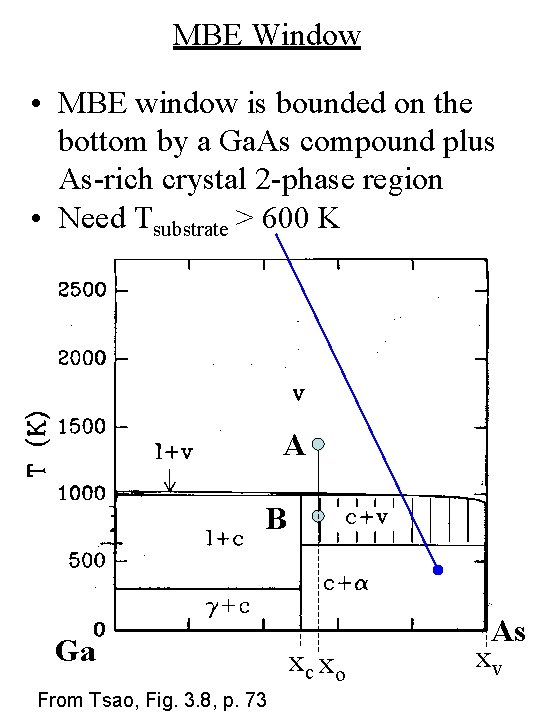
MBE Window • MBE window is bounded on the bottom by a Ga. As compound plus As-rich crystal 2 -phase region • Need Tsubstrate > 600 K A B Ga From Tsao, Fig. 3. 8, p. 73 xc xo As xv

MBE Window • Otherwise, excess As condenses into rhombohedral crystal structure, <As>a • Low-temperature MBE From Tsao, Fig. 3. 10, p. 76

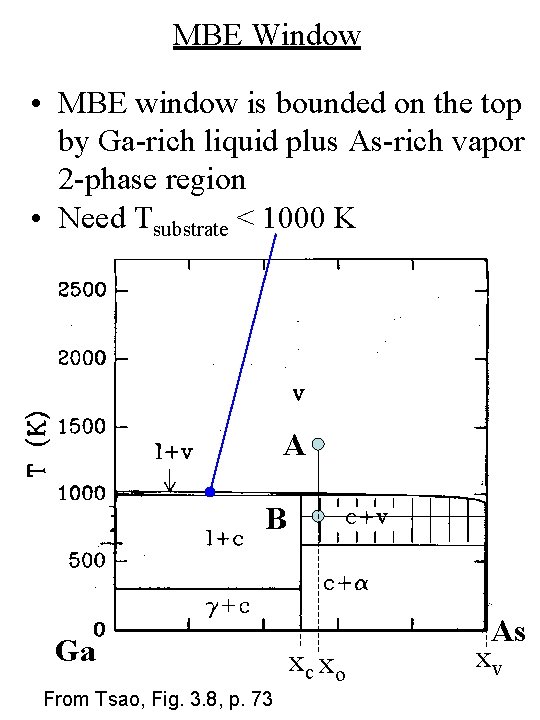
MBE Window • MBE window is bounded on the top by Ga-rich liquid plus As-rich vapor 2 -phase region • Need Tsubstrate < 1000 K A B Ga From Tsao, Fig. 3. 8, p. 73 xc xo As xv

MBE Window • Otherwise Ga. As will decompose into Ga liquid and As 2 vapor From Tsao, Fig. 3. 9, p. 75

Binary Alloys Regular Solutions G = x. AGA + x. BGB + DGmix = DHmix –TDSmix From Porter & Easterling, Fig. 1. 15(c) & (d), p. 20

Binary Alloys • e. g. , mixture of In. As and Ga. As to form In 1 -x. Gax. As • lattice constants: a. In. As = 6. 0584 Å, a. Ga. As = 5. 6533 Å • DHmix > 0 due to the bond bending and stretching from equilibrium positions • Randomly mixed solution is thermodynamically unstable • In. As and Ga. As bonds are preferred compared to average In. Ga. As bonds • G is lowered by phase separating into In. As-rich and Ga. As-rich regions From Porter & Easterling, Fig. 1. 18(a) & (b), p. 23

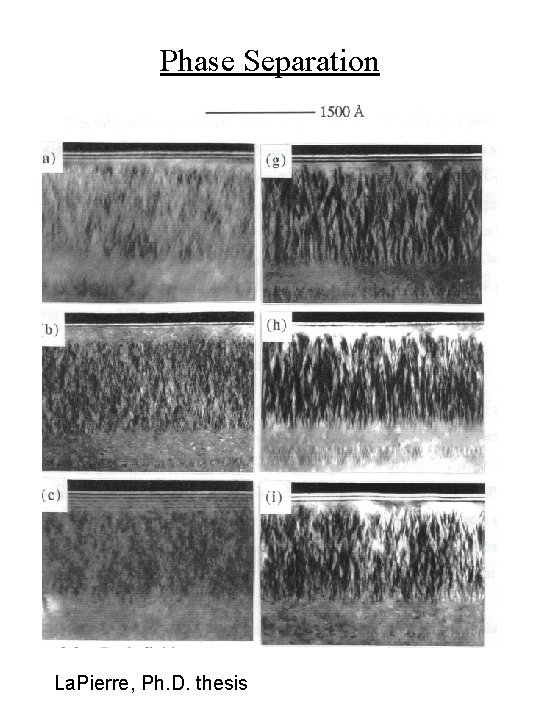
Phase Separation La. Pierre, Ph. D. thesis

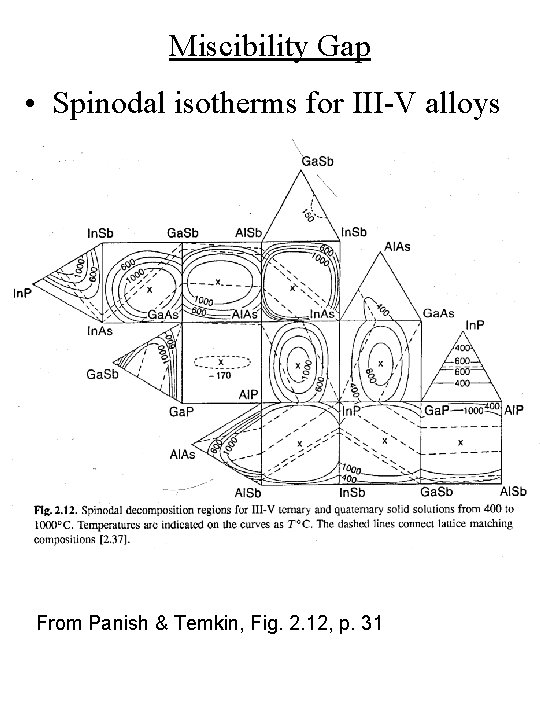
Miscibility Gap • Spinodal isotherms for III-V alloys From Panish & Temkin, Fig. 2. 12, p. 31