PGT 205 1 4 0 Laplace Transform 4

PGT 205 1

4. 0 Laplace Transform. 4. 1 4. 2 4. 3 4. 4 4. 5 4. 6 4. 7 Introduction. The Laplace Transform. The Unilateral Transform and Properties. Inversion of the Unilateral. Properties of the Bilateral Laplace Transform Properties of the Region of Convergence. The Transfer Function 2

4. 1 Introduction. In Chapter 3 we developed representation of signal and LTI by using superposition of complex sinusoids. þ In this Chapter 4 we are considering the continuous-time signal and system representation based on complex exponential signals. þ The Laplace transform can be used to analyze a large class of continuous-time problems involving signal that are not absolutely integrable, such as impulse response of an unstable system. þ Laplace transform come in two varieties; varieties (i) Unilateral (one sided); is a tool for solving differential equations with initial condition. þ (ii) Bilateral (two sided); offer insight into the nature of system characteristic such as stability, causality, and frequency response. 3

Pierre-Simon Laplace 3/23/1749 - 3/2/1827 4

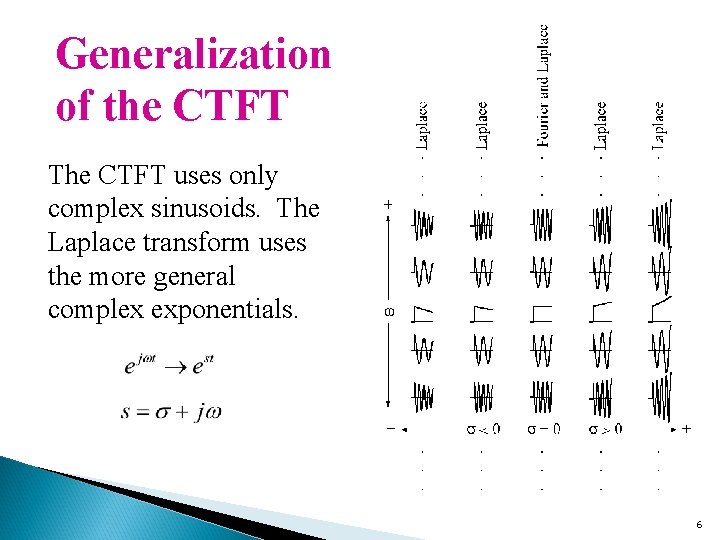
Generalization of the CTFT Laplace Transform is more general than Fourier Transform. The FT is really just a special case of the LT. 5

Generalization of the CTFT The CTFT uses only complex sinusoids. The Laplace transform uses the more general complex exponentials. 6

4. 2 Laplace Transform. þ Let est be a complex exponential with complex frequency s = s +jw. We may write, The real part of est is an exponential damped cosine þ And the imaginary part is an exponential damped sine þ The real part of s is the exponential damping factor s. þ And the imaginary part of s is the frequency of the cosine and sine factor, w. þ 7

4. 2. 1 Eigen Function Property of est. þ Apply an input to the form x(t) =est to an LTI system with impulse response h(t). The system output is given by, Derivation: þ We use x(t) =est to obtain þ We define transfer function as 8

Cont’d… þ We can write þ An Eigen function is a signal that passes through the system without being modified except by multiplication by scalar. þ The equation below indicates that, - est is the Eigen function of the LTI system. - H(s) is the Eigen value. 9

4. 2. 2 Laplace Transform Representation. H(s) is the Laplace Transform of h(t) and the h(t) is the inverse Laplace transform of H(s). þ The Laplace transform of x(t) is þ þ The Inverse Laplace Transform of X(s) is þ We can express the relationship with the notation 10

4. 2. 3 Convergence. þ The condition for convergence of the Laplace transform is the absolute integrability of x(t)e-at , þ The range of s for which the Laplace transform converges is termed the region of convergence (ROC) 11

4. 2. 4 The s-Plane. þ It is convenience to represent the complex frequency s graphically in termed the s-plane. (i) the horizontal axis represents the real part of s (exponential damping factor s). (ii) The vertical axis represents the imaginary part of s (sinusoidal frequency w) In s-plane, s =0 correspond to imaginary axis. þ Fourier transfrom is given by the Laplace transform evaluated along the imaginary axis. þ 12

4. 2. 5 Poles and Zeros. þ Zeros. The ck are the root of the numerator polynomial and are termed the zeros of X(s). Location of zeros are denoted as “o”. þ Poles. The dk are the root of the denominator polynomial and are termed the poles of X(s). Location of poles are denoted as “x”. þ The Laplace transform does not uniquely correspond to a signal x(t) if the ROC is not specified. þ Two different signal may have identical Laplace Transform, but different ROC. Below is the example. Figure 4. 4 a Figure 4. 4 b Figure 4. 4 a. The ROC for x(t) = eatu(t) is depicted by the shaded region. A pole is located at s = a. Figure 4. 4 b. The ROC for y(t) = –eatu(–t) is depicted by the shaded region. A pole is located at s = a. 13

Example 4. 1: Laplace Transform of a Causal Exponential Signal. Determine the Laplace transform of x(t)=eatu(t). And Sketch the Zero and Pole. Solution: Step 1: Find the Laplace transform. To evaluate e-(s-a)t, Substitute s=s + jw 14

Cont’d… If s > a, then e-(s-a)t goes to zero as t approach infinity, *The Lapalce transform does not exist for s=<a because the integral does not converge. *The ROC is at s>a, the shade region of the s-plane in Figure below. The pole is at s=a. 4. 5: The ROC for x(t) = eatu(t) is depicted by the shaded region. A pole ýFigure. is located at s = a. 15

Properties Let g(t) and h(t) both be causal functions and let them form the following transform pairs, Linearity Time Shifting Complex-Frequency Shifting 16

Properties Time Scaling Frequency Scaling Time Differentiation Once Nth Time Derivative 17

Properties Complex-Frequency Differentiation Multiplication-Convolution Duality Integration 2/19/2021 18

4. 3 The Unilateral Laplace Transform and Properties. þ The Unilateral Laplace Transform of a signal x(t) is defined by þ The lower limit of 0 - implies that we do include discontinuities and impulses that occur at t = 0 in the integral. H(s) depends on x(t)for t >= 0. þ The relationship between X(s) and x(t) as þ The unilateral and bilateral Laplace transforms are equivalent for signals that are zero for time t<0. 19

4. 4 Inversion of the Unilateral Laplace Transform. þ We can determine the inverse Laplace transforms using one-toone relationship between the signal and its unilateral Laplace transform. þ X(s) is the sum of simple terms, þ Using the residue method, solve for a system linear equation. þ Then sum the Inverse Laplace transform of each term. 20

Example 4. 3: Inversion by Partial-Fraction Expansion. Find the Inverse Laplace Transform of Solution: Step 1: Use the partial fraction expansion of X(s) to write Solving the A, B and C by the method of residues 21

Cont’d… 22

Cont’d… A=1, B=-1 and C=2 Step 2: Construct the Inverse Laplace transform from the above partial-fraction term above. - The pole of the 1 st term is at s = -1, so - The pole of the 2 nd term is at s = -2, so -The double pole of the 3 rd term is at s = -2, so Step 3: Combining the terms. ý. 23

Example 4. 4: Inversion An Improper Rational Laplace Transform. Find the Inverse Laplace Transform of Solution: Step 1: Use the long division to espress X(s) as sum of rational polynomial function. We can write, 24

Cont’d… Use partial fraction to expand the rational function, Step 2: Construct the Inverse Laplace transform from the above partial-fraction term above. Refer to the Laplace transform Table. ý. 25

4. 5 Properties of Bilateral Laplace Transform. þ The Bilateral Lapalace Transform is suitable to the problems involving no causal signals and system. þ The properties of linearity, scaling, s-domain shift, convolution and differentiation in the s-domain is identical fort the bilateral and unilateral LT, the operations associated y these properties may change the ROC. þ Example; a linearity property. þ ROC of the sum of the signals is an intersection of the individual ROCs. 26

4. 6 Properties of Region of Converges. þ The Bilateral Lapalace Transform is suitable to the problems involving non causal signals and system. þ The properties of linearity, scaling, s-domain shift, convolution and differentiation in the s-domain is identical for the bilateral and unilateral LT, the operations associated y these properties may change the ROC. þ ROC of the sum of the signals is an intersection of the individual ROCs. 27

4. 7 Transfer Function. þ The transfer function of an LTI system is defined as the Laplace transform of the impulse response. þ Take the bilateral Laplace transform of both sides of the equation and use the convolution properties result in, þ Rearrange the above equation result in the ratio of Laplace transform of the output signal to the Laplace transform of the input signal. (X(s) is nonzero) 28