PG lectures Particle Physics Introduction C Lazzeroni www

PG lectures- Particle Physics Introduction C. Lazzeroni www. ep. ph. bham. ac. uk/user/lazzeroni/pglectures

Outline - Properties and classification of particles and forces - leptons and hadrons - mesons and baryons - forces and bosons - Relativistic kinematics - particle production and decays - cross sections and lifetimes - centre-of-mass and lab frames - invariant mass - Summary of Standard Model - Feynman diagrams - QED - QCD - Weak interactions - Conservation laws - conserved quantum numbers and symmetries - allowed and forbidden reactions

Outline - Angular momentum and Spin - basic quantum mechanics - Clebsch-Gordon coefficients - conservation of angular momentum and spin - Isospin - combination. , conservation - pion-nucleon scattering - C, P, CPT - application in quark model - neutral kaon mixing - CP violation - CKM matrix - weak decays of quarks - quark mixing - CPV in SM

essential books - Quarks and Leptons, F. Halzen and A. D. Martin - Modern Particle Physics, M. Thomson - Particle physics, B. R. Martin and G. Shaw - Introduction to High Energy Physics, 2 nd ed. , D. H. Perkins - Review of Particle Physics, PDG

useful books - Detectors for particle radiation, K. Kleinknecht - Large Hadron Collider Phenomenology, M. Kramer and F. J. P. Soler - Particle Detectors, C. Grupen and B. Shwartz - QCD and collider physics, R. K. Ellis and W. J. Stirling and B. R. Webber - A modern introduction to Quantum Field Theory, M. Maggiore - Prestigious discoveries at CERN, R. Cashmore, L. Maiani, J. P. Revol - An introduction to relativistic processes and the Standard Model of Electroweak Interactions, C. M. Becchi and G. Ridolfi - Handbook of accelerator physics and engineering, A. Wu Chao and M. Tigner - Statistical methods in experimental physics, F. James

Section 1 - matter and forces

We now know that all matter is made of two types of elementary particles (spin ½ fermions): LEPTONS: e. g. e-, ne QUARKS: e. g. up quark (u) and down quark (d) proton (uud) A consequence of relativity and quantum mechanics is that for every particle there exists an antiparticle which has identical mass, spin, energy, momentum, BUT has the opposite sign interaction. ANTIPARTICLES: e. g. positron e+ , antiquarks (u, d), antiproton (uud) 7

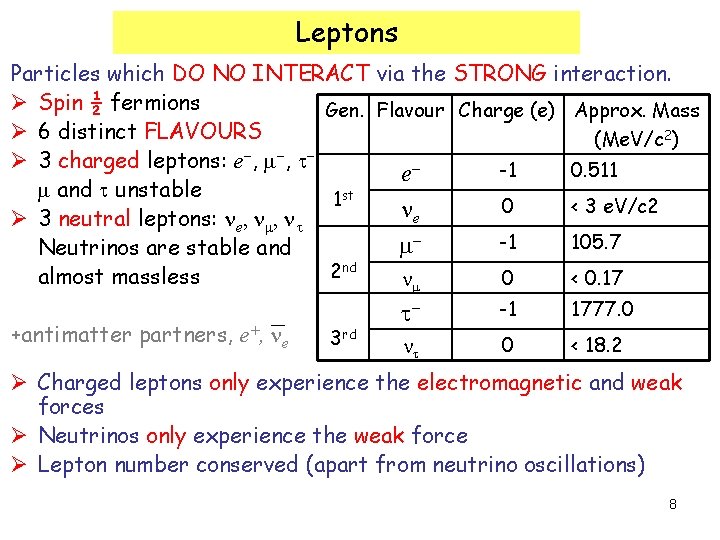
Leptons Particles which DO NO INTERACT via the STRONG interaction. Ø Spin ½ fermions Gen. Flavour Charge (e) Approx. Mass Ø 6 distinct FLAVOURS (Me. V/c 2) Ø 3 charged leptons: e , m , -1 0. 511 e m and unstable 1 st 0 < 3 e. V/c 2 ne Ø 3 neutral leptons: ne, nm, n -1 105. 7 m Neutrinos are stable and nd 2 almost massless 0 < 0. 17 nm +antimatter partners, e+, ne 3 rd -1 1777. 0 n 0 < 18. 2 Ø Charged leptons only experience the electromagnetic and weak forces Ø Neutrinos only experience the weak force Ø Lepton number conserved (apart from neutrino oscillations) 8

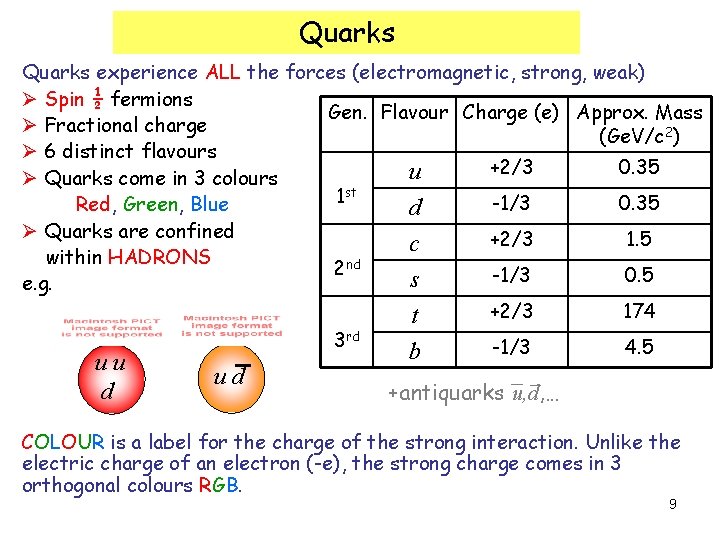
Quarks experience ALL the forces (electromagnetic, strong, weak) Ø Spin ½ fermions Gen. Flavour Charge (e) Approx. Mass Ø Fractional charge (Ge. V/c 2) Ø 6 distinct flavours +2/3 0. 35 u Ø Quarks come in 3 colours 1 st -1/3 0. 35 Red, Green, Blue d Ø Quarks are confined +2/3 1. 5 c within HADRONS 2 nd -1/3 0. 5 s e. g. +2/3 174 t 3 rd -1/3 4. 5 uu d ud b +antiquarks u, d, … COLOUR is a label for the charge of the strong interaction. Unlike the electric charge of an electron (-e), the strong charge comes in 3 orthogonal colours RGB. 9

Hadrons Ø Single free quarks are NEVER observed, but are always CONFINED in bound states, called HADRONS. Ø Macroscopically hadrons behave as point-like COMPOSITE particles. Hadrons are of two standard types: MESONS (qq) Bound states of a QUARK and an ANTIQUARK All have INTEGER spin 0, 1, 2, … Bosons e. g. BARYONS (qqq) Bound states of 3 QUARKS All have HALF-INTEGER spin 1/2, 3/2, … Fermions e. g. PLUS ANTIBARYONS e. g. qq qq q 10

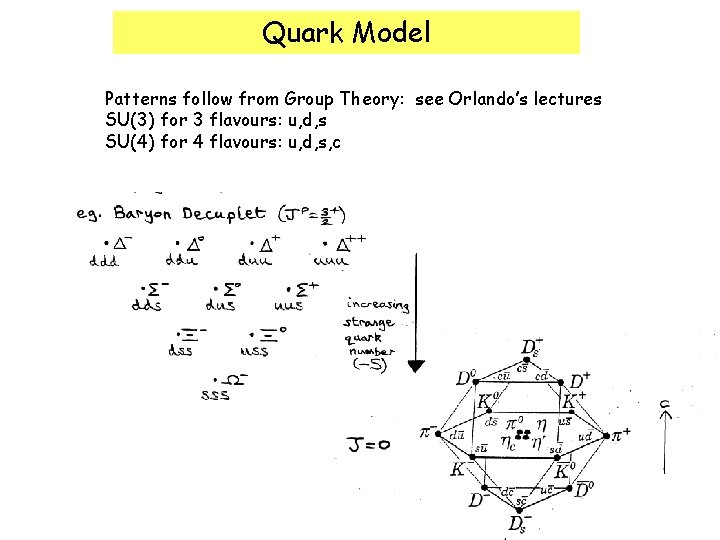
Quark Model Patterns follow from Group Theory: see Orlando’s lectures SU(3) for 3 flavours: u, d, s SU(4) for 4 flavours: u, d, s, c

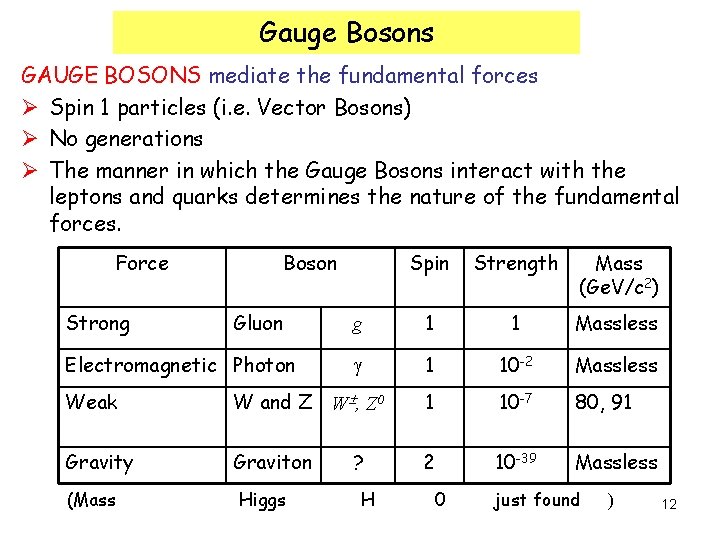
Gauge Bosons GAUGE BOSONS mediate the fundamental forces Ø Spin 1 particles (i. e. Vector Bosons) Ø No generations Ø The manner in which the Gauge Bosons interact with the leptons and quarks determines the nature of the fundamental forces. Force Strong Boson Gluon Electromagnetic Photon Spin Strength Mass (Ge. V/c 2) g 1 1 Massless 1 10 -2 Massless Weak W and Z W , Z 0 1 10 -7 80, 91 Gravity Graviton ? 2 10 -39 Massless (Mass Higgs H 0 just found ) 12

Range of Forces The range of a force is directly related to the mass of the exchanged bosons. Force Range (m) Strong (Nuclear) 10 -15 Electromagnetic Weak Gravity 10 -18 13

Section II - Relativistic kinematics

Natural Units Ø Choose energy as basic unit of measurement Energy Momentum Mass Ge. V/c 2 Time (Ge. V/ ħ)-1 Length (Ge. V/ ħc)-1 Cross-section (Ge. V/ ħc) -2 Ø Simplify by choosing ħ=c=1 Energy Momentum Mass Ge. V Time Ge. V-1 Length Ge. V-1 Cross-section Ge. V-2 Ø Convert back to SI units by reintroducing “missing” factors of ħ and c ħc = 0. 197 Ge. V fm ħ = 6. 6 x 10 -25 Ge. V s 15

Relativistic Kinematics Ø In Special Relativity, the total energy and momentum of a particle of mass m are and are related by Note: At rest, E = m and for E >>m, E ~ p Ø The K. E. is the extra energy due to motion In the non-relativistic limit Ø Particle physics T is of O (100 Ge. V) >> rest energies relativistic formulas. Ø Always treat decay relativistically. 16

In Special Relativity reference, BUT and transform between frames of Invariant interval INVARIANT MASS are CONSTANT. 17

Four-Vectors Ø Define FOUR-VECTORS: where Ø Scalar product of two four-vectors Invariant: Lorentz metric (opposed to Minkowski) or 18

Colliders and √s Consider the collision of two particles: The invariant quantity is the energy in the zero momentum (centre-of-mass) frame It is the amount of energy available to interaction e. g. the maximum energy/mass of a particle produced in matter-antimatter annihilation. 19

Fixed Target Collision For e. g. 100 Ge. V proton hitting a proton at rest: Collider Experiment For then and e. g. 100 Ge. V proton colliding with a 100 Ge. V proton: In a fixed target experiment most of the proton’s energy is used to provide momentum to the C. O. M system rather than being available 20 for the interaction.

1) Transform from a particle rest frame to a frame in which particle has velocity =v/c p 0 = 0 , E 0 =m p 1, E 1 Equivalent to boosting frame of reference in opposite direction - : p 1 = p 0 + E 0 = m E 1 = E 0 + p 0 = m 2) Calculate invariant mass M of AB system: p. A = (EA , p. A ) p. B = (EB , p. B ) E A 2 = | P A |2 + M A 2 EB 2 = | PB |2 + MB 2 M 2 = (EA + EB)2 - (p. A + p. B)2 = = EA 2 + 2 EA EB + EB 2 - ( |p. A|2 + 2 p. A p. B + | p. B|2 ) = = MA 2 + MB 2 + 2 ( EA EB - p. A p. B )

3) Rapidity: useful in hadron-hadron collisions, related to longitudinal momentum distribution |p. L | = |p| cos y = 1/2 ln ( E + p. L ) / ( E - p. L) y = ln (E + p. L ) / ( p. T 2 + m 2) Rapidity y is not Lorentz invariant but y distribution (shape) remains unchanged under Lorentz boost Lorentz transform to frame moving with relative velocity along the beam direction causes a constant offset y 0 = y + 1/2 ln ( 1 - ) / ( 1+ )

Section III - decay rates

How do we study particles and forces ? Ø Static Properties Mass, spin and parity (JP), magnetic moments, bound states Ø Particle Decays Allowed/forbidden decays Conservation Laws Ø Particle Scattering Direct production of new massive particles in matter/antimatter ANNIHILATION Study of particle interaction cross-sections. Force Typical Lifetime (s) Typical Cross-section (mb) Strong 10 -23 10 Electromagnetic 10 -20 10 -2 Weak 10 -8 10 -13 24

Particle Decays Most particles are transient states – only the privileged few live forever (e , u, d, , …) A decay is the transition from one quantum state (initial state) to another (final or daughter). The transition rate is given by FERMI’S GOLDEN RULE: where Mfi r (Ef) is the number of transitions per unit time is the matrix element is the density of final states. dt is the probability a particle will decay in time dt. 25

1 particle decay Let p(t) be the probability that a particle will survive until at least time t, if it is known to exist at t=0. Prob. particle decays in the next time dt = p(t) dt Prob. particle survives in the next time dt = p(t)(1 - dt)= p(t+dt) EXPONENTIAL DECAY LAW 26

Probability that a particle lives until time t and then decays in time dt is Ø The AVERAGE LIFETIME of the particle Ø Finite lifetime UNCERTAIN energy DE Ø Decaying states do not correspond to a single energy – they have a width DE ħ =1 natural units Ø The width, DE, of a particle state is – Inversely proportional to the lifetime – Equal to the transition rate using natural units. 27

Many particles Ø NUMBER of particles at time t, where N(0) is the number at time t=0. Ø RATE OF DECAYS Ø ACTIVITY Ø HALF-LIFE i. e. the time over which 50% of the particles decay 28

Decaying States Resonances QM description of decaying states Consider a state with energy E 0 and lifetime i. e. the probability density decays exponentially (as required). The frequencies present in the wavefunction are given by the Fourier transform of Probability of finding state with energy E = f(E)*f(E) 29

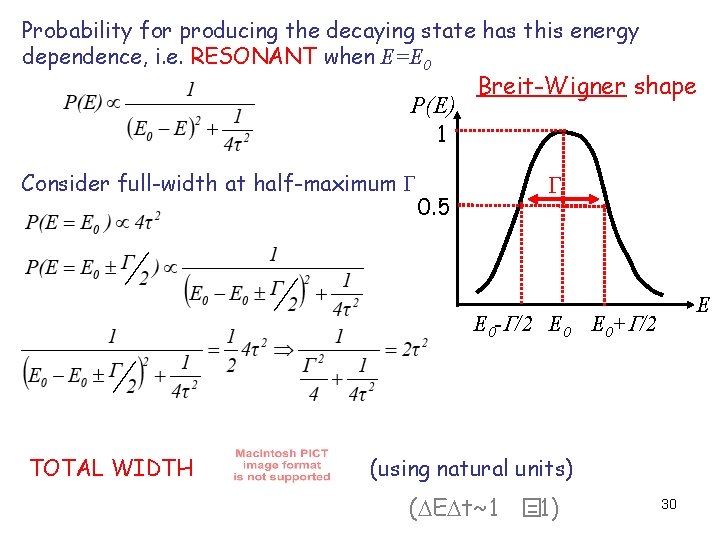
Probability for producing the decaying state has this energy dependence, i. e. RESONANT when E=E 0 P(E) Breit-Wigner shape 1 Consider full-width at half-maximum G 0. 5 G E E 0 -G/2 E 0+G/2 TOTAL WIDTH (using natural units) (DEDt~1 � =1) 30

Partial Decay Widths Particles can often decay with more than one decay mode, each with its own transition rate Ø The TOTAL DECAY RATE is given by Ø This determines the AVERAGE LIFETIME Ø The TOTAL WIDTH of a particle state is Ø DEFINE the PARTIAL WIDTHS Ø The proportion of decays to a particular decay mode is called the BRANCHING FRACTION 31

Section III - reactions

Reactions and Cross-sections The strength of a particular reaction between two particles is specified by the interaction CROSS-SECTION. A cross-section is an effective target area presented to the incoming particle for it to cause the reaction. UNITS: s 1 barn (b) = 10 -28 m 2 Area The cross-section, s, is defined as the reaction rate per target particle, G, per unit incident flux, F where the flux, F, is the number of beam particles passing through unit area per second. G is given by Fermi’s Golden Rule 33

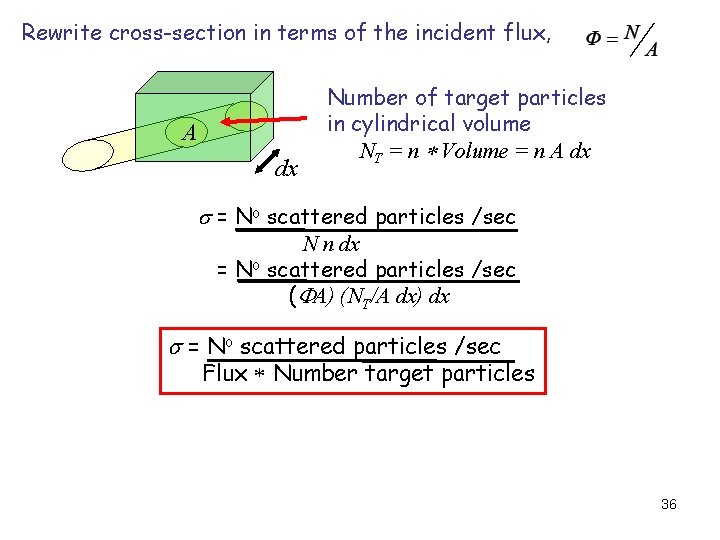
Consider a beam of particles incident upon a target: Target n nuclei/unit volume Beam N particles/sec dx A Number of target particles in area A = n A dx Effective area for absorption = s n A dx Rate at which particles are = d. N = N s n A dx removed from beam A d. N = s n dx N s = No scattered particles /sec N n dx 34

Beam attenuation in a target (thickness L) Ø thick target (s n L>>1) Ø thin target (s n L<<1, e -s n L 1 -s n L) MEAN FREE PATH between interactions = 1 /ns For nuclear interactions: nuclear interaction length For electromagnetic interactions: radiation length 35

Rewrite cross-section in terms of the incident flux, A dx Number of target particles in cylindrical volume NT = n Volume = n A dx s = No scattered particles /sec N n dx = No scattered particles /sec (FA) (NT/A dx) dx s = No scattered particles /sec Flux Number target particles 36

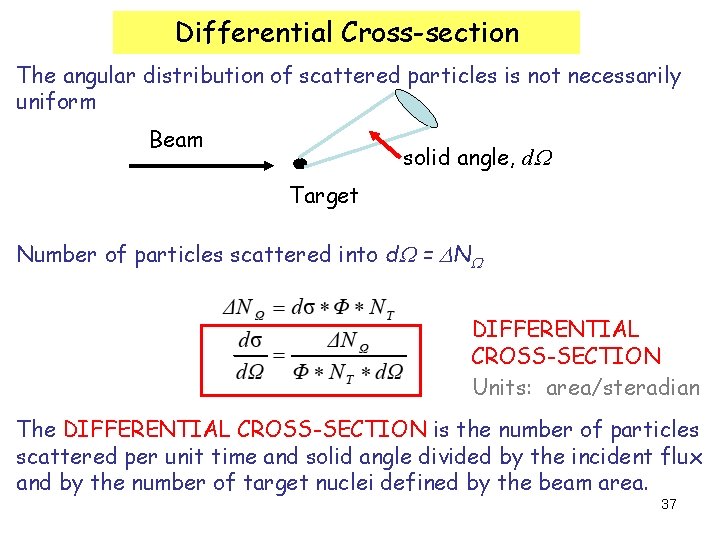
Differential Cross-section The angular distribution of scattered particles is not necessarily uniform Beam solid angle, d. W Target Number of particles scattered into d. W = DNW DIFFERENTIAL CROSS-SECTION Units: area/steradian The DIFFERENTIAL CROSS-SECTION is the number of particles scattered per unit time and solid angle divided by the incident flux and by the number of target nuclei defined by the beam area. 37

Ø Most experiments do not cover 4 p and in general we use ds/d. W. Ø Angular distributions provide more information about the mechanism of the interaction. Ø Different types of interaction can occur between particles. where the si are called PARTIAL CROSS-SECTIONS. Types of interaction: Elastic scattering: a+b Inelastic scattering: only momenta of a and b change a + b c + d + …… final state not the same as initial state XY ! PQ = exclusive XY ! anything = inclusive 38