PFTWBTh l l l Review Priority Queues and

PFTWBTh l l l Review Priority Queues and O(log N) Ø Binary search, binary trees, binary heaps Review for Midterm Ø Source code provided Ø Handouts/What you bring Ø What you bring, how you work on exam, lessons learned from Midterm I (both sides) Toward Huffman Coding Ø Priority Queues and Data compressions Compsci 201, Fall 2016 22. 1

WOTO http: //bit. ly/201 fall 16 -nov 16 More review possible Compsci 201, Fall 2016 22. 2

Priority Queue top-M sorting l What if we have lots and lots of data Ø code below sorts top-M elements, complexity? Scanner s = … // initialize; Priority. Queue<String> pq = new Priority. Queue<String>(); while (s. has. Next()) { pq. add(s. next()); if (pq. size() > M) pq. remove(); } l What's advantageous about this code? Ø Store everything and sort everything? Ø Store everything, sort first M? Ø What is complexity of sort: O(n log n) Compsci 201, Fall 2016 22. 3

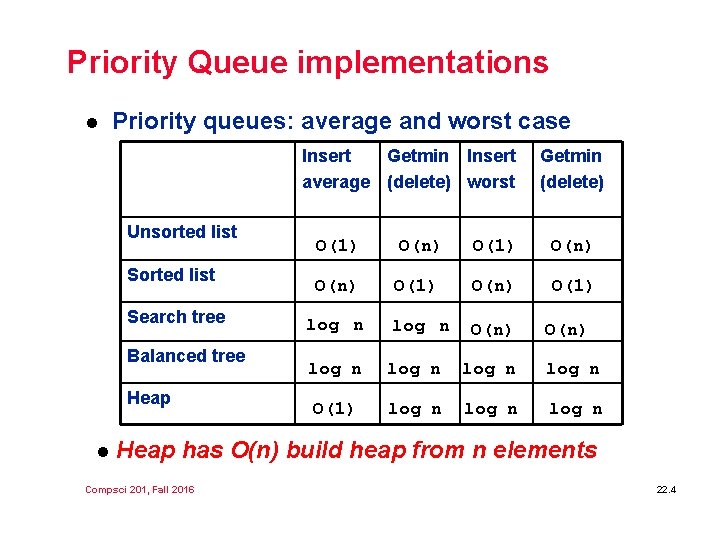
Priority Queue implementations l Priority queues: average and worst case Insert Getmin Insert average (delete) worst Unsorted list Search tree Balanced tree Heap l Getmin (delete) O(1) O(n) O(1) log n O(n) log n O(1) log n O(n) Heap has O(n) build heap from n elements Compsci 201, Fall 2016 22. 4

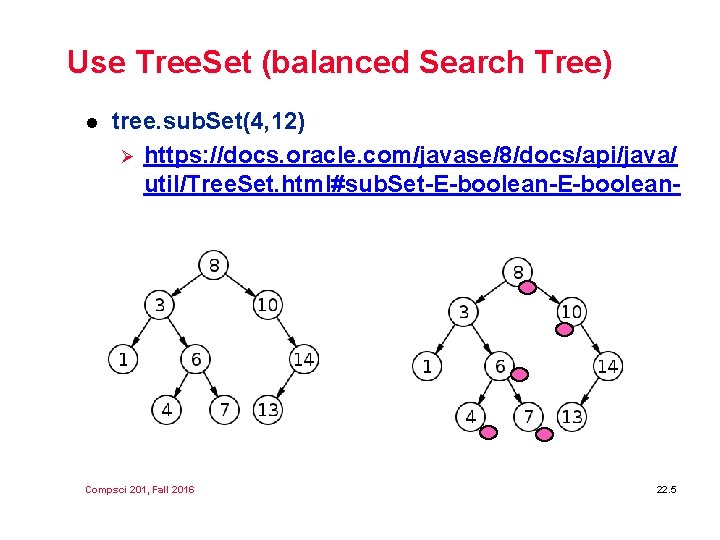
Use Tree. Set (balanced Search Tree) l tree. sub. Set(4, 12) Ø https: //docs. oracle. com/javase/8/docs/api/java/ util/Tree. Set. html#sub. Set-E-boolean- Compsci 201, Fall 2016 22. 5

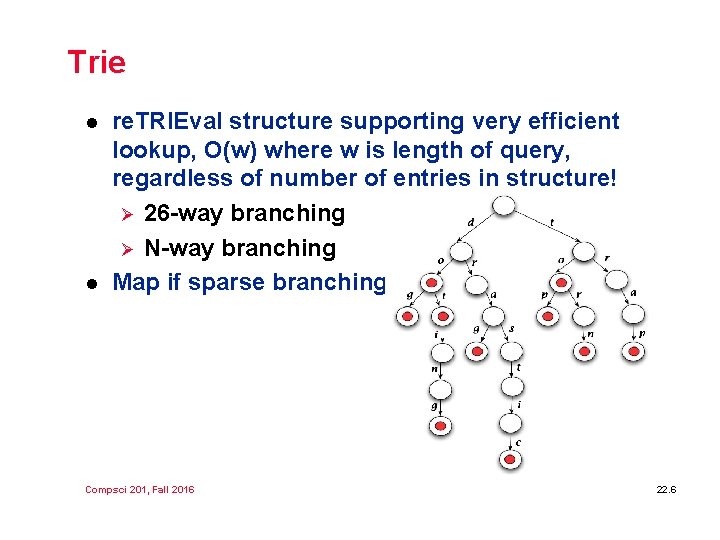
Trie l l re. TRIEval structure supporting very efficient lookup, O(w) where w is length of query, regardless of number of entries in structure! Ø 26 -way branching Ø N-way branching Map if sparse branching Compsci 201, Fall 2016 22. 6

Trie, and Trie again l https: //git. cs. duke. edu/201 fall 16/set-examples/blob/master/src/Trie. Set. java l Method. contains is similar to others Ø What does Node class look like? public boolean contains(String s) { Node t = my. Root; for (int k = 0; k < s. length(); k++) { char ch = s. char. At(k); t = t. children. get(ch); if (t == null) return false; // no path below? done } return t. is. Word; // was this marked as a word? } Compsci 201, Fall 2016 22. 7

Priority Queue implementation l Heap data structure is fast and reasonably simple Ø Uses array, contiguous memory, good performance with cache and more l Changing comparison when calculating priority? Ø Create object to replace, or in lieu of compare. To • Comparable interface compares this to passed object • Comparator interface compares two passed objects Ø Comparisons: compare. To() and compare() • Compare two objects (parameters or self and parameter) • Returns – 1, 0, +1 depending on <, ==, > Compsci 201, Fall 2016 22. 8

Creating Heaps l Heap: array-based implementation of binary tree used for implementing priority queues: Ø add/insert, peek/getmin, remove/deletemin, O(? ? ? ) Array minimizes storage (no explicit pointers), faster too, contiguous (cache) and indexing l Heap has shape property and heap/value property Ø shape: tree filled at all levels (except perhaps last) and filled left-to-right (complete binary tree) Ø each node has value smaller than both 22. 9 Compsci 201, Fall 2016 children l

Views of programming l Writing code from the method/function view is pretty similar across languages Ø Organizing methods is different, organizing code is different, not all languages have classes, Ø Loops, arrays, arithmetic, … Program using abstractions and high level concepts Ø Do we need to understand 32 -bit twoscomplement storage to understand x =x+1? Ø Do we need to understand how arrays map to 22. 10 Compsci 201, Fall 2016 contiguous memory to use Array. Lists? l

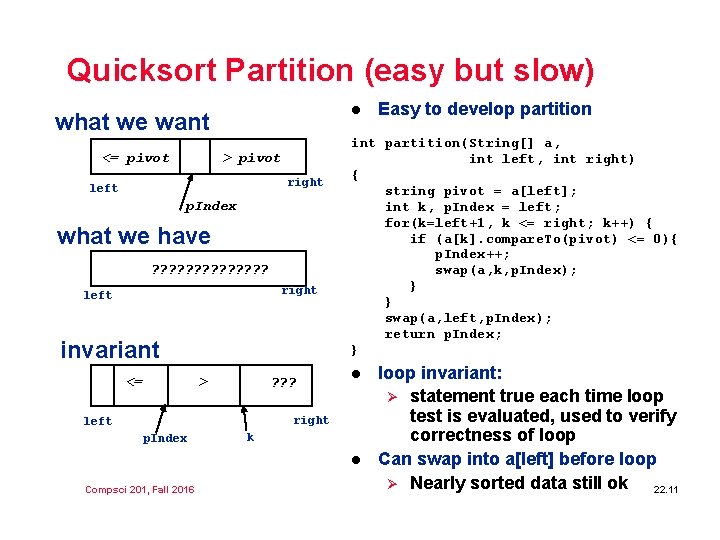
Quicksort Partition (easy but slow) l what we want <= pivot > pivot right left p. Index what we have ? ? ? ? right left invariant <= > ? ? ? int partition(String[] a, int left, int right) { string pivot = a[left]; int k, p. Index = left; for(k=left+1, k <= right; k++) { if (a[k]. compare. To(pivot) <= 0){ p. Index++; swap(a, k, p. Index); } } swap(a, left, p. Index); return p. Index; } l right left p. Index k l Compsci 201, Fall 2016 Easy to develop partition loop invariant: Ø statement true each time loop test is evaluated, used to verify correctness of loop Can swap into a[left] before loop Ø Nearly sorted data still ok 22. 11

Developing Loops l l The Science of Programming, David Gries The Discipline of Programming, Edsger Disjkstra Compsci 201, Fall 2016 22. 12

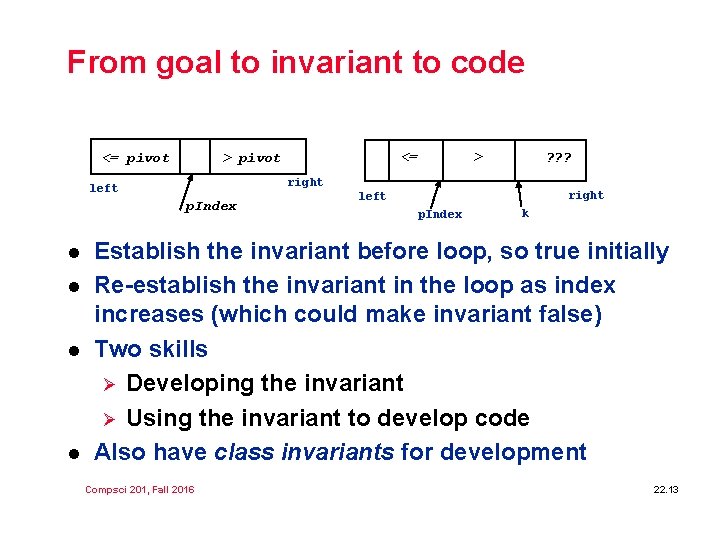
From goal to invariant to code <= pivot p. Index l l l > ? ? ? right left l <= > pivot right left p. Index k Establish the invariant before loop, so true initially Re-establish the invariant in the loop as index increases (which could make invariant false) Two skills Ø Developing the invariant Ø Using the invariant to develop code Also have class invariants for development Compsci 201, Fall 2016 22. 13

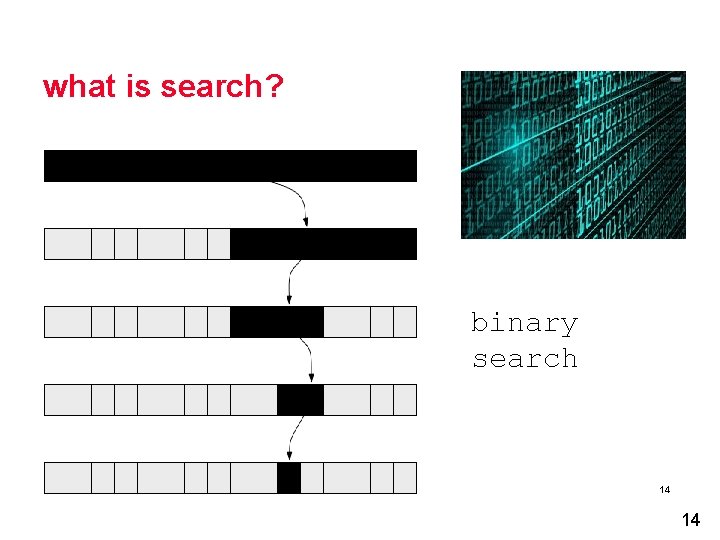
what is search? binary search We Teach_CS, Austin, 2016 14 14

Why write the binary search method? l After all, there is Collections. binary. Search Ø Which of several equal keys found? 1, 1, 2, 2, 2, 3, 3, 3 Ø Why does this matter? l Look up the code online!? *!#? Ø http: //stackoverflow. com/questions/6676360/fir st-occurrence-in-a-binary-search Why did you take Compsci 201? Ø How to write/develop? How to randomly permute and hope? Search skills? Compsci 201, Fall 2016 l 22. 15

Coding Interlude: Reason about code public class Looper { public static void main(String[] args){ int x = 0; while (x < x + 1) { x = x + 1; } System. out. println("value of x = "+x); } } We Teach_CS, Austin, 2016 16

What does this code do? int x = 0; A. while (x < x + 1) { B. x = x + 1; } System. out. println(x); C. D. Compsci 201, Fall 2016 Runs Forever Runs until memory exhausted (a few seconds with 8 Gb) Runs for a second, prints about 2 billion Runs for a second, prints about -2 billion 22. 17

From idea to code http: //bit. ly/ap-csa public static int binary. Search(int[] elements, int target){ int left = 0; int right = elements. length − 1; while (left <= right) { int mid = (left + right) / 2; if (target < elements[mid]) right = mid − 1; else if (target > elements[middle]) left = mid + 1; else return mid; } return − 1; } We Teach_CS, Austin, 2016 18 18

http: //googleresearch. blogspot. com/2006/06/extra-read-all-about-itnearly. html public static int binary. Search(int[] elements, int target) { int left = 0; int right = elements. length − 1; while (left <= right) { int mid = (left + right) / 2; if (target < elements[mid]) right = mid − 1; else if (target > elements[middle]) left = mid + 1; else return mid; } return − 1; } We Teach_CS, Austin, 2016 19 19

What should you remember? 10 2 = 1, 024 31 2 is about 2 billion Store that many values in memory? We Teach_CS, Austin, 2016 20 20

Don't know much about algebra (left + right)/2 (right - left)/2 + left right/2 - left/2 + 2*left/2 right/2 + left/2 (right + left)/2 We Teach_CS, Austin, 2016 21 21

Huffman Coding l l Understand Huffman Coding Ø Data compression Ø Priority Queue Ø Bits and Bytes Ø Greedy Algorithm Many compression algorithms Ø Huffman is optimal, per-character compression Ø Still used, e. g. , basis of Burrows-Wheeler Ø Other compression 'better', sometimes slower? Ø LZW, GZIP, BW, … Compsci 201, Fall 2016 22. 22

Compression and Coding l What gets compressed? Ø Save on storage, why is this a good idea? Ø Save on data transmission, how and why? l What is information, how is it compressible? Ø Exploit redundancy, without that, hard to compress Represent information: code (Morse cf. Huffman) Ø Dots and dashes or 0's and 1's Ø How to construct code? l Compsci 201, Fall 2016 22. 23

PQ Application: Data Compression l Compression is a high-profile application Ø. zip, . mp 3, . jpg, . gif, . gz, … Ø What property of MP 3 was a significant factor in what made Napster work (why did Napster ultimately fail? ) Why do we care? Ø Secondary storage capacity doubles every year Ø Disk space fills up there is more data to compress than ever before Ø Ever need to stop worrying about storage? Compsci 201, Fall 2016 l 22. 24

More on Compression l l Different compression techniques Ø. mp 3 files and. zip files? Ø. gif and. jpg? Impossible to compress/lossless everything: Why? Lossy methods Ø pictures, video, and audio (JPEG, MPEG, etc. ) Lossless methods Ø Run-length encoding, Huffman 11 3 5 3 2 6 5 3 5 3 10 Compsci 201, Fall 2016 22. 25

Coding/Compression/Concepts l For ASCII we use 8 bits, for Unicode 16 bits Ø Minimum number of bits to represent N values? Ø Representation of genomic data (a, c , g, t)? Ø What about noisy genomic data? l We can use a variable-length encoding, e. g. , Huffman Ø How do we decide on lengths? How do we decode? Ø Values for Morse code encodings, why? Ø … ---… Compsci 201, Fall 2016 22. 26

Huffman Coding D. A Huffman in early 1950’s: story of invention Ø Analyze and process data before compression Ø Not developed to compress data “on-the-fly” l Represent data using variable length codes Ø Each letter/chunk assigned a codeword/bitstring Ø Codeword for letter/chunk is produced by traversing the Huffman tree Ø Property: No codeword produced is the prefix of another Ø Frequent letters/chunk have short encoding, while those that appear rarely have longer ones l Huffman coding is optimal per-character coding method 22. 27 Compsci 201, Fall 2016 l

Mary Shaw l Software engineering and software architecture Ø Tools for constructing large software systems Ø Development is a small piece of total cost, maintenance is larger, depends on welldesigned and developed techniques l Interested in computer science, programming, curricula, and canoeing, health-care costs ACM Fellow, Alan Perlis Professor of Compsci at CMU l Compsci 201, Fall 2016 22. 28

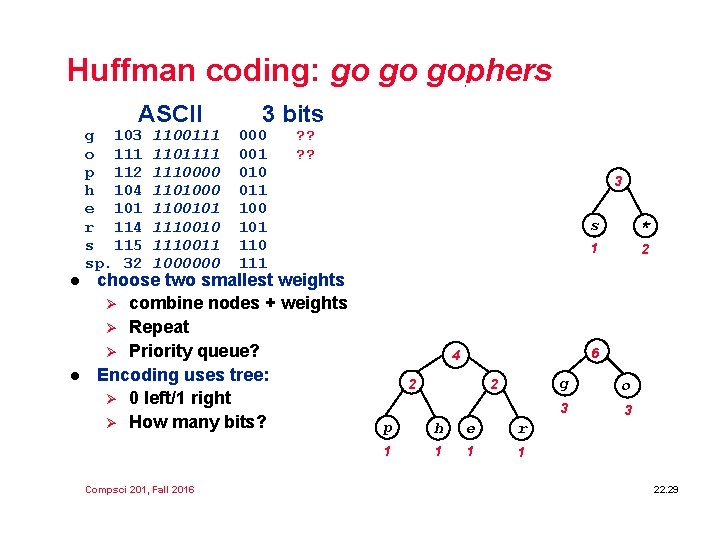
Huffman coding: go go gophers ASCII g 103 o 111 p 112 h 104 e 101 r 114 s 115 sp. 32 l l 1100111 1101111 1110000 1101000 1100101 1110010 1110011 1000000 3 bits 000 001 010 011 100 101 110 111 ? ? choose two smallest weights Ø combine nodes + weights Ø Repeat Ø Priority queue? Encoding uses tree: Ø 0 left/1 right Ø How many bits? Compsci 201, Fall 2016 g o p h e r s * 3 3 1 1 1 2 2 2 3 p h e r s * 1 1 1 2 6 4 2 2 p h e r 1 1 g o 3 3 22. 29

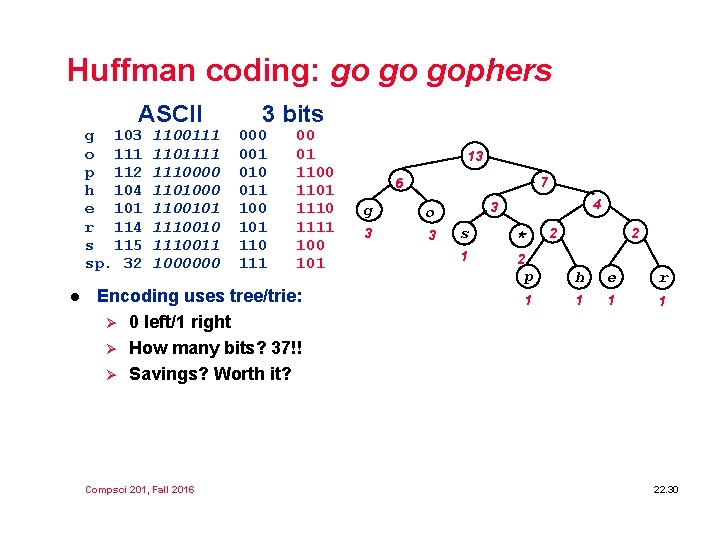
Huffman coding: go go gophers ASCII g 103 o 111 p 112 h 104 e 101 r 114 s 115 sp. 32 l 1100111 1101111 1110000 1101000 1100101 1110010 1110011 1000000 3 bits 000 001 010 011 100 101 110 111 00 01 1100 1101 1110 1111 100 101 13 7 6 g o 3 3 Encoding uses tree/trie: Ø 0 left/1 right Ø How many bits? 37!! Ø Savings? Worth it? 4 3 s * 1 2 2 2 p h e r 1 1 6 4 2 2 g o 3 3 3 Compsci 201, Fall 2016 p h e r 1 1 s * 1 2 22. 30

Building a Huffman tree l Begin with a forest of single-node trees/tries (leaves) Ø Each node/tree/leaf is weighted with character count Ø Node stores two values: character and count l Repeat until there is only one node left: root of tree Ø Remove two minimally weighted trees from forest Ø Create new tree/internal node with minimal trees as children, • Weight is sum of children’s weight (no char) How does process terminate? Finding minimum? l Ø Remove minimal trees, hummm…… Compsci 201, Fall 2016 22. 31

How do we create Huffman Tree/Trie? l Insert weighted values into priority queue Ø What are initial weights? Why? Ø l Remove minimal nodes, weight by sums, re-insert Ø Total number of nodes? Priority. Queue<Tree. Node> pq = new Priority. Queue<Tree. Node>(); for(int k=0; k < freq. length; k++){ pq. add(new Tree. Node(k, freq[k], null)); } while (pq. size() > 1){ Tree. Node left = pq. remove(); Tree. Node right = pq. remove(); pq. add(new Tree. Node(0, left. weight+right. weight, left, right)); } Tree. Node root = pq. remove(); Compsci 201, Fall 2016 22. 32

Creating compressed file l Once we have new encodings, read every character Ø Write encoding, not the character, to compressed file Ø Why does this save bits? Ø What other information needed in compressed file? l How do we uncompress? Ø How do we know foo. hf represents compressed file? Ø Is suffix sufficient? Alternatives? Why is Huffman coding a two-pass method? Compsci Fall 2016 Ø 201, Alternatives? l 22. 33

Uncompression with Huffman l We need the trie to uncompress Ø 00010011001101111 l As we read a bit, what do we do? Ø Go left on 0, go right on 1 Ø When do we stop? What to do? l How do we get the trie? Ø How did we get it originally? Store 256 int/counts • How do we read counts? Ø How do we store a trie? 20 Questions relevance? • Reading a trie? Leaf indicator? Node values? Compsci 201, Fall 2016 22. 34

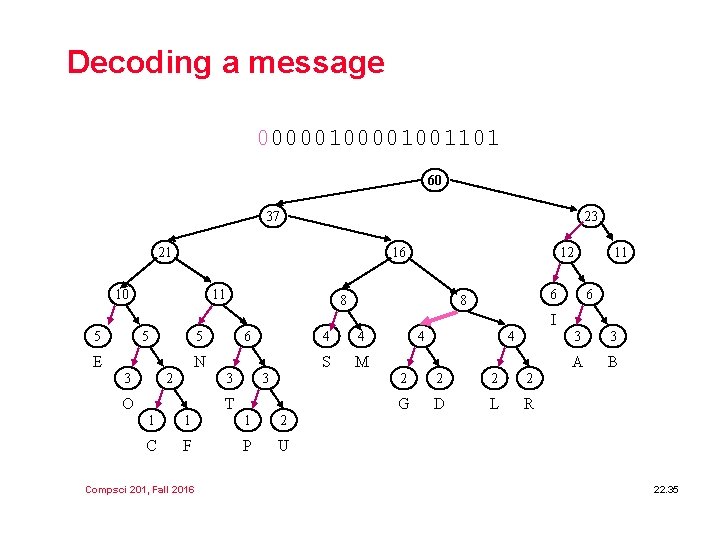
Decoding a message 000001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 4 4 S M 4 4 2 2 G D L R 3 3 A B 22. 35

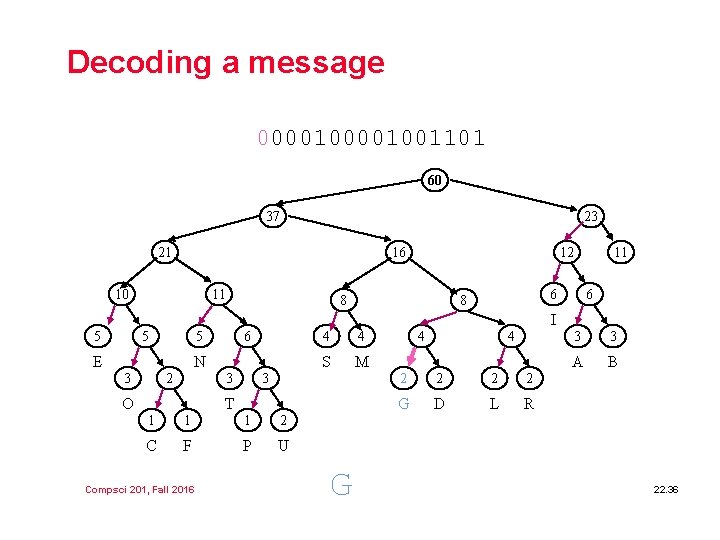
Decoding a message 00001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 G 4 4 2 2 G D L R 3 3 A B 22. 36

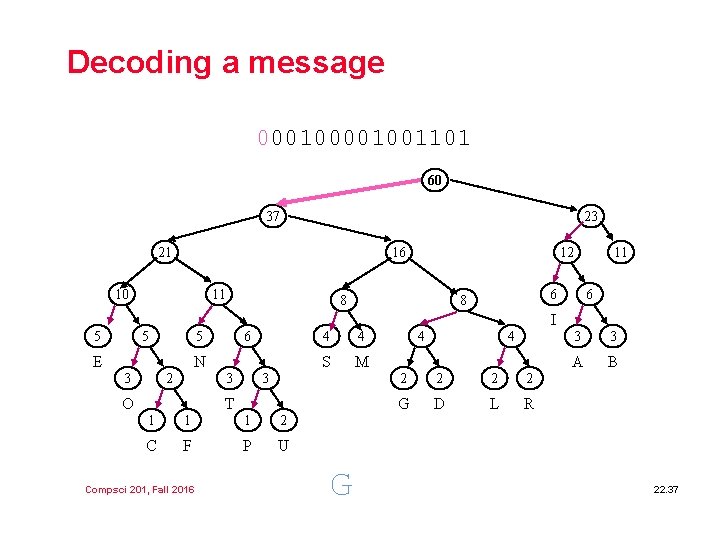
Decoding a message 0001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 G 4 4 2 2 G D L R 3 3 A B 22. 37

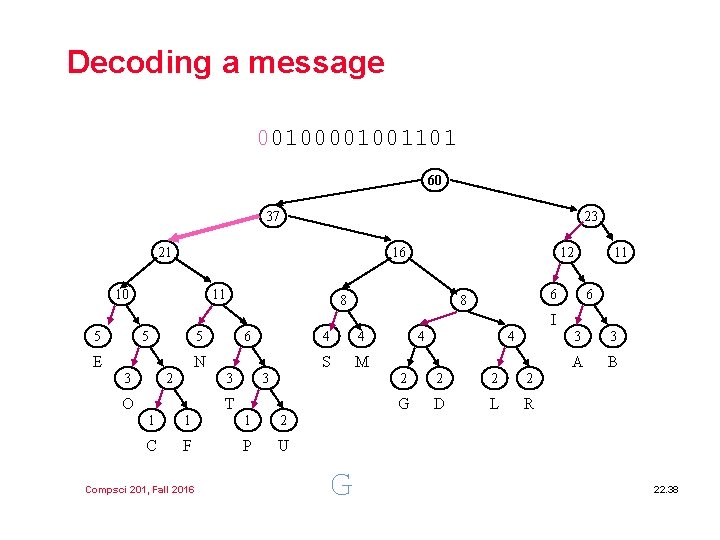
Decoding a message 001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 G 4 4 2 2 G D L R 3 3 A B 22. 38

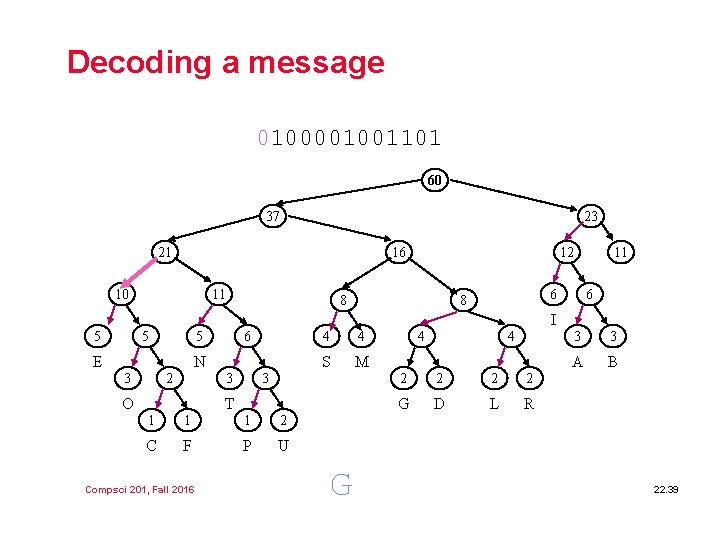
Decoding a message 0100001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 G 4 4 2 2 G D L R 3 3 A B 22. 39

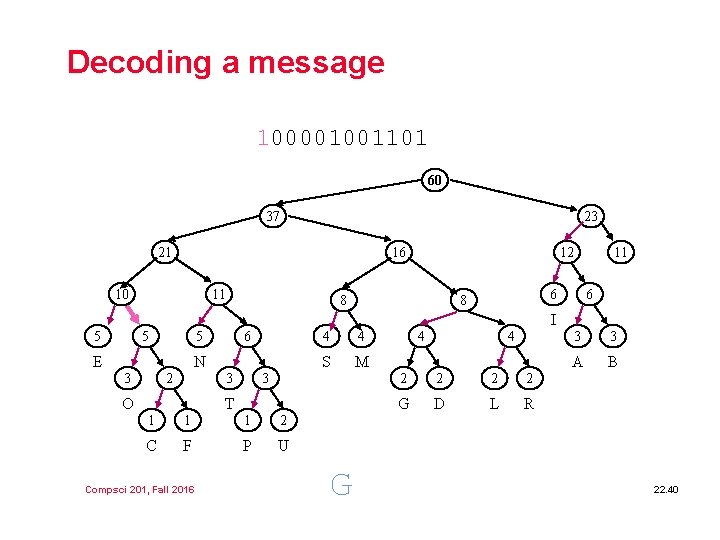
Decoding a message 100001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 G 4 4 2 2 G D L R 3 3 A B 22. 40

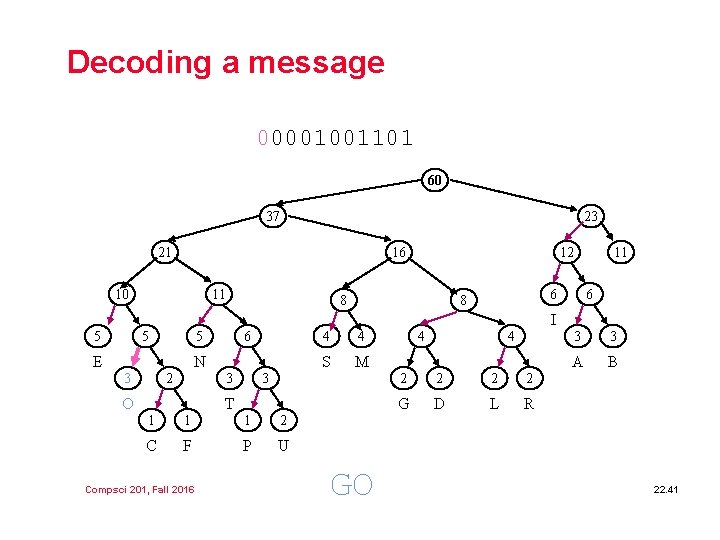
Decoding a message 00001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GO 4 4 2 2 G D L R 3 3 A B 22. 41

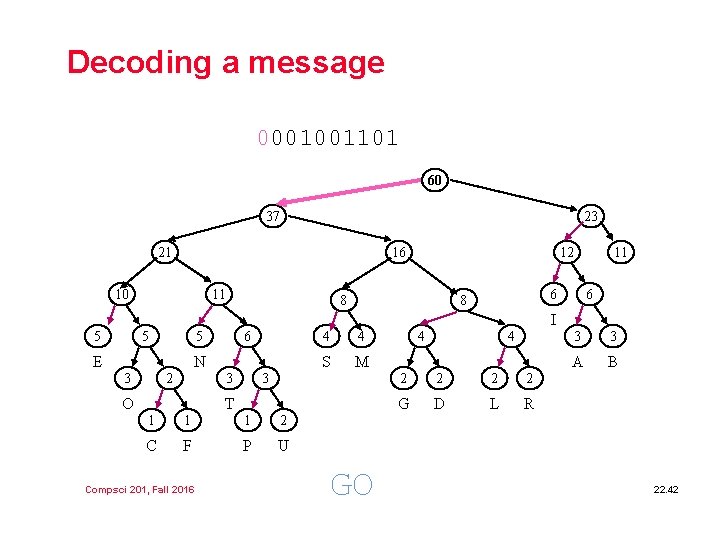
Decoding a message 0001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GO 4 4 2 2 G D L R 3 3 A B 22. 42

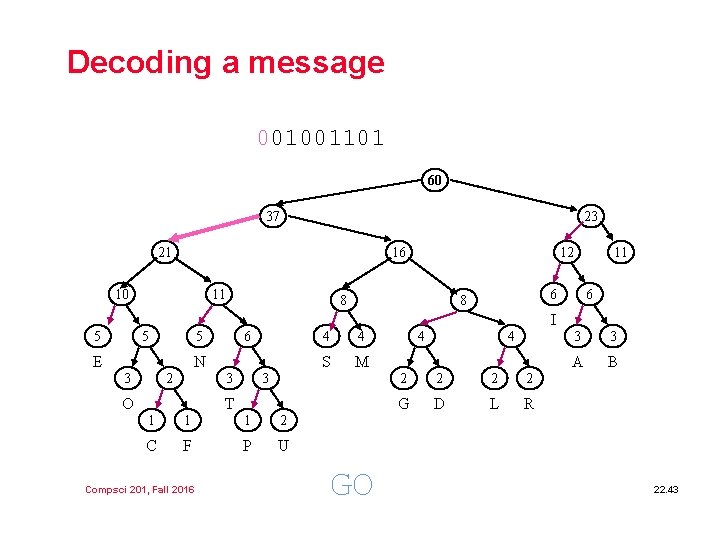
Decoding a message 001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GO 4 4 2 2 G D L R 3 3 A B 22. 43

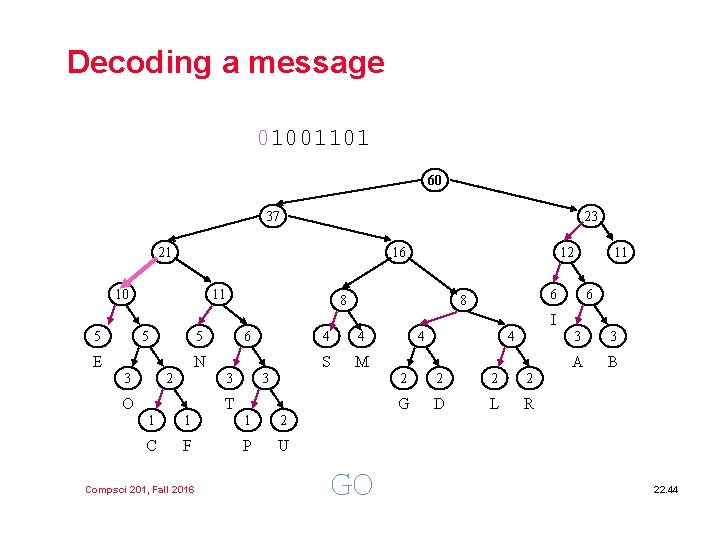
Decoding a message 01001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GO 4 4 2 2 G D L R 3 3 A B 22. 44

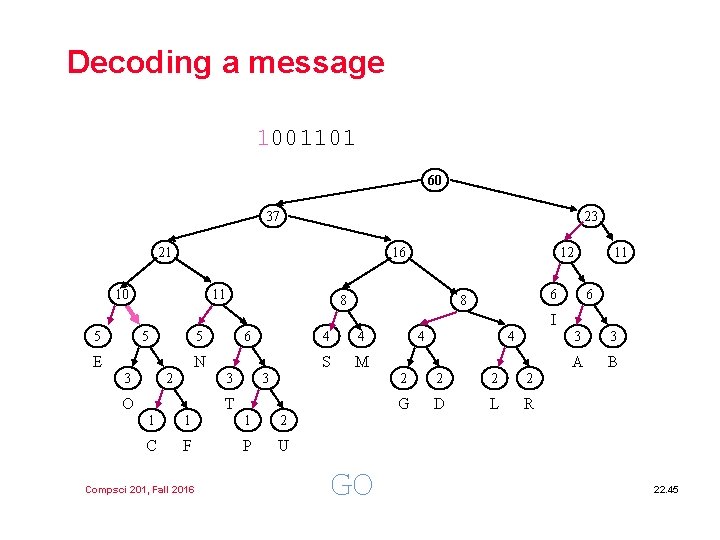
Decoding a message 1001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GO 4 4 2 2 G D L R 3 3 A B 22. 45

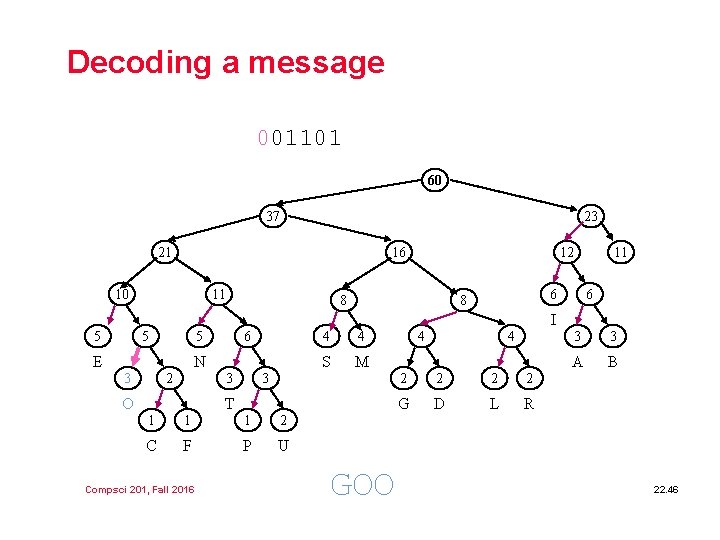
Decoding a message 001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GOO 4 4 2 2 G D L R 3 3 A B 22. 46

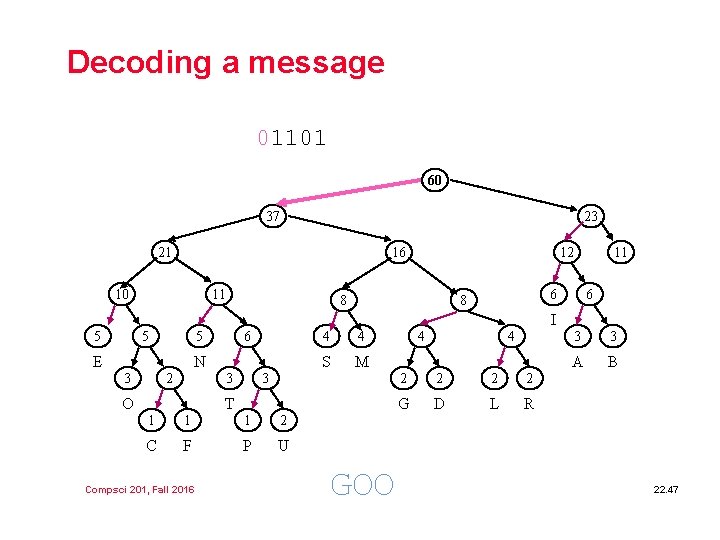
Decoding a message 01101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GOO 4 4 2 2 G D L R 3 3 A B 22. 47

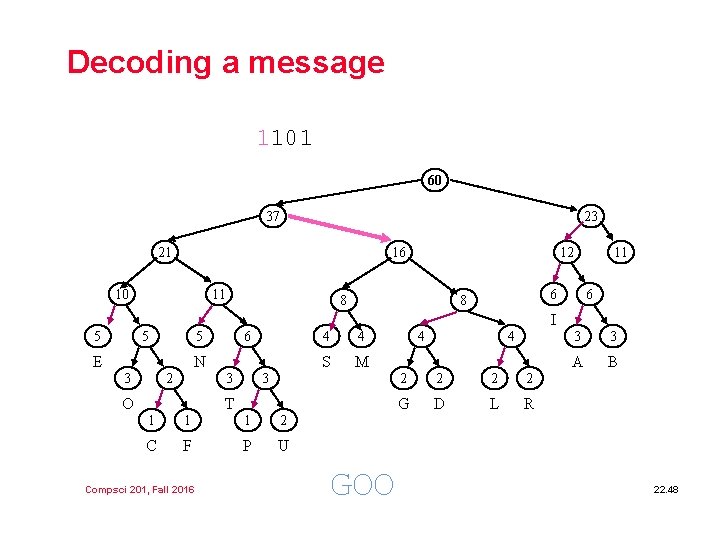
Decoding a message 1101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GOO 4 4 2 2 G D L R 3 3 A B 22. 48

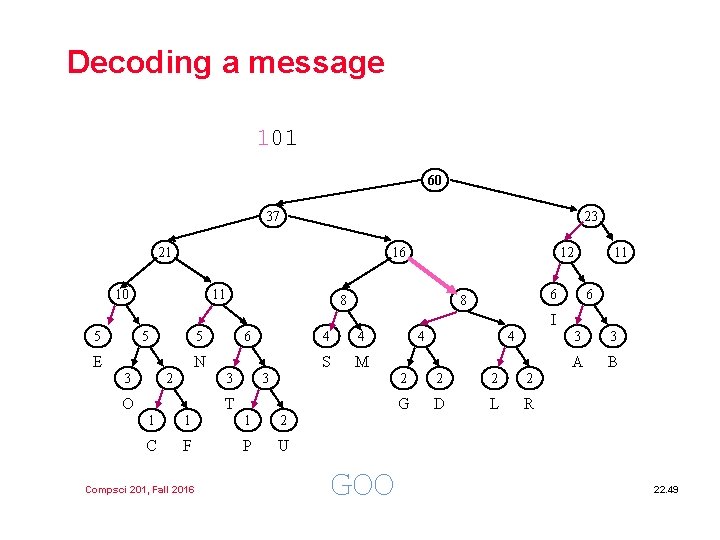
Decoding a message 101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GOO 4 4 2 2 G D L R 3 3 A B 22. 49

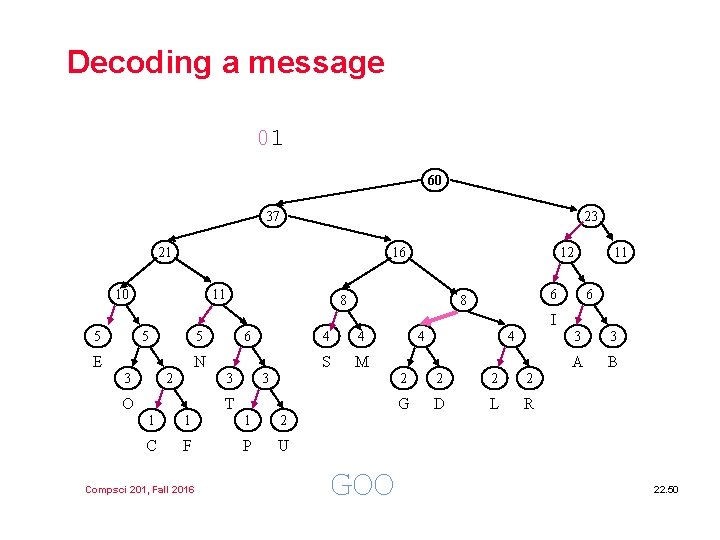
Decoding a message 01 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 4 4 S M 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 GOO 4 4 2 2 G D L R 3 3 A B 22. 50

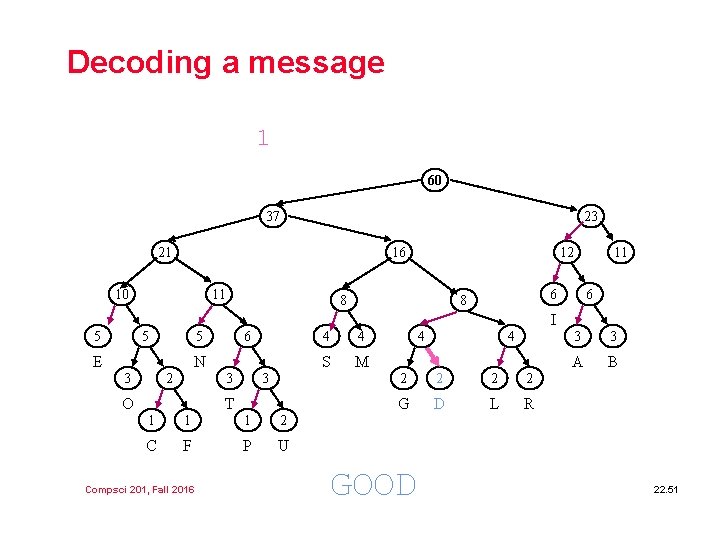
Decoding a message 1 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 4 4 S M 4 4 2 2 G D L R GOOD 3 3 A B 22. 51

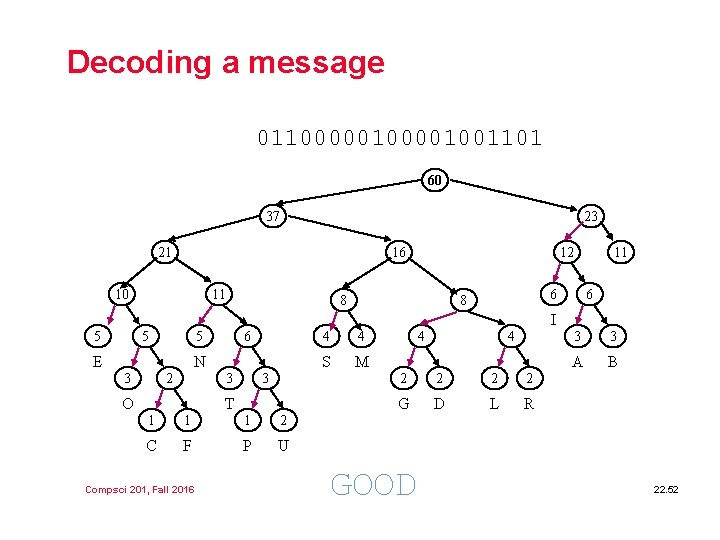
Decoding a message 011000001001101 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E 6 N 3 2 3 O 3 T 1 1 1 2 C F P U Compsci 201, Fall 2016 4 4 S M 4 4 2 2 G D L R GOOD 3 3 A B 22. 52

Other Huffman Issues l What do we need to decode? Ø How did we encode? How will we decode? Ø What information needed for decoding? l Reading and writing bits: chunks and stopping Ø Can you write 3 bits? Why not? Why? Ø PSEUDO_EOF Ø Bit. Input. Stream and Bit. Output. Stream: API l What should happen when the file won’t compress? Ø Silently compress bigger? Warn user? Alternatives? Compsci 201, Fall 2016 22. 53

Huffman Complexities l How do we measure? Size of input file, size of alphabet Ø Which is typically bigger? l Accumulating character counts: ______ Ø How can we do this in O(1) time, though not really Building the heap/priority queue from counts ____ Ø Initializing heap guaranteed Building Huffman tree ____ Ø Why? Create table of encodings from tree ____ Ø Why? Write tree and compressed file _____ l l Compsci 201, Fall 2016 22. 54