PETSc Portable Extensible Toolkit for Scientific computing Overview

PETSc Portable, Extensible Toolkit for Scientific computing

Overview n n Parallel & Sequential Object-oriented Available for virtually all UNIX platforms, as well as Windows 95/NT Flexible: many options for solver algorithms and parameters

Motivation n n Developing parallel, non-trivial PDE solvers that deliver high performance is still difficult and requires months (or even years) of concentrated effort. PETSc is a toolkit that can ease these difficulties and reduce the development time

Introduction n A freely available and supported research code n n n Available via http: //www. mcs. anl. gov/petsc Free for everyone, including industrial users Hyperlinked documentation and manual pages for all routines. Many tutorial-style examples Support via email: petsc-maint@mcs. anl. gov Usable from Fortran 77/90, C, and C++ Portable to any parallel system supporting MPI, including n Tightly coupled systems n n Cray T 3 E, SGI Origin, IBM SP, HP 9000, Sun Enterprise Loosely coupled systems, e. g. , networks of workstations n Compaq, HP, IBM, SGI, Sun, PCs running Linux or Windows

History n PETSc history n Begun in September 1991 n Keep on development n Now: over 8, 500 downloads since 1995 (versions 2. 0 and 2. 1)

PETSc Concepts n How to specify the mathematics of the problem n n - vectors, matrices How to solve the problem n n Data objects Solvers - linear, nonlinear, and time stepping (ODE) solvers Parallel computing complications n Parallel data layout - structured and unstructured meshes
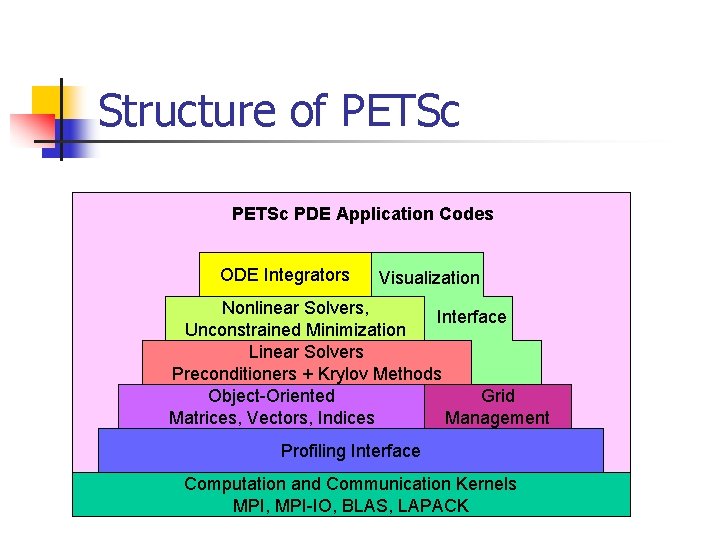
Structure of PETSc PDE Application Codes ODE Integrators Visualization Nonlinear Solvers, Interface Unconstrained Minimization Linear Solvers Preconditioners + Krylov Methods Object-Oriented Grid Matrices, Vectors, Indices Management Profiling Interface Computation and Communication Kernels MPI, MPI-IO, BLAS, LAPACK
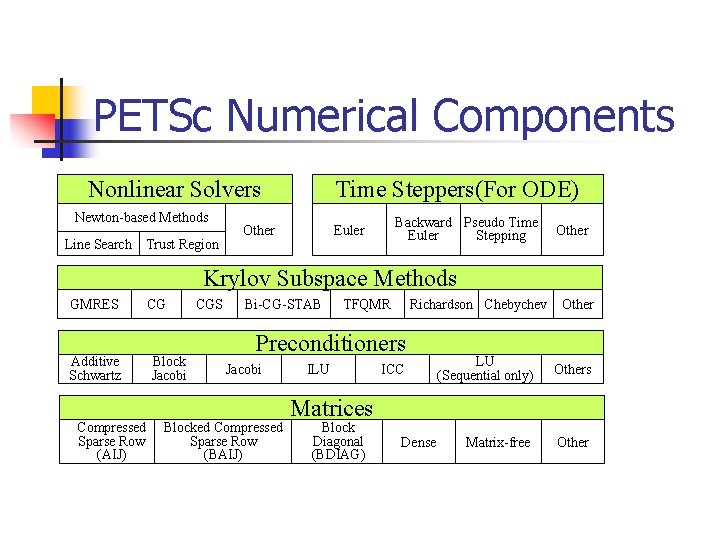
PETSc Numerical Components Nonlinear Solvers Newton-based Methods Line Search Trust Region Time Steppers(For ODE) Other Backward Pseudo Time Euler Stepping Euler Other Krylov Subspace Methods GMRES Additive Schwartz Compressed Sparse Row (AIJ) CG Block Jacobi CGS Bi-CG-STAB TFQMR Richardson Chebychev Preconditioners Jacobi Blocked Compressed Sparse Row (BAIJ) ILU ICC Other LU (Sequential only) Others Matrix-free Other Matrices Block Diagonal (BDIAG) Dense

What is not in PETSc? n n Discretizations Unstructured mesh generation and refinement tools n Load balancing tools n Sophisticated visualization capabilities

BUT! PETSc has interface to external software that provides some of this functionality n Linear solvers (AMG Block. Solve 95 LUSOL SPAI Super. LU) n Optimization software (TAO, Veltisto) n Mesh and discretization tools (overture, SAMRAI) n ODE solvers (PVODE) n Others (Matlab, Par. METIS)
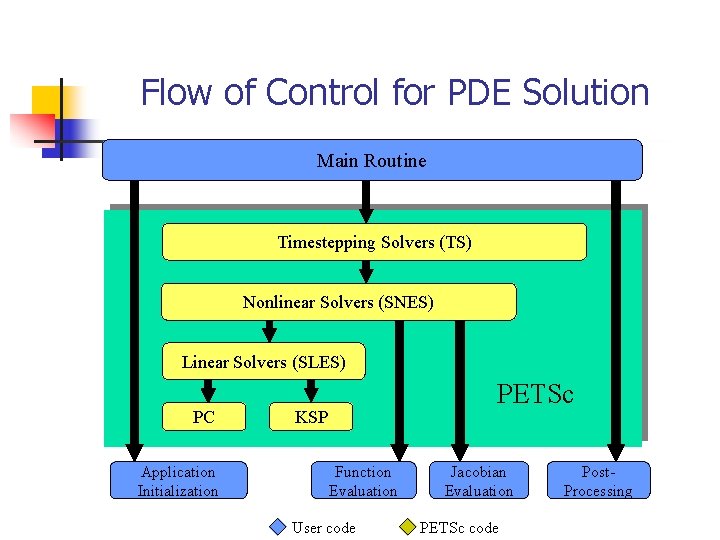
Flow of Control for PDE Solution Main Routine Timestepping Solvers (TS) Nonlinear Solvers (SNES) Linear Solvers (SLES) PC Application Initialization PETSc KSP Function Evaluation User code Jacobian Evaluation PETSc code Post. Processing
![A simple PETSc program #include “petsc. h” int main( int argc, char *argv[] ) A simple PETSc program #include “petsc. h” int main( int argc, char *argv[] )](http://slidetodoc.com/presentation_image/ffc41c8c800ef6d8df3eb5278950f91d/image-12.jpg)
A simple PETSc program #include “petsc. h” int main( int argc, char *argv[] ) { int rank; Petsc. Initialize(&argc, &argv, PETSC_NULL); MPI_Comm_rank(PETSC_COMM_WORLD, &rank ); Petsc. Synchronized. Printf(PETSC_COMM_WORLD, “Hello World from %dn”, rank); Petsc. Finalize(); return 0; }

Sparse Matrix Computation in PETSc n Variety Data Structures n Variety Preconditioners n Variety Iterative Solvers n Variety interface to External Softwares

Data Structure for sparse matrix n Compressed Sparse Row n Blocked compressed sparse Row n Block Diagonal

Example(BCRS) n Block Compressed Sparse Row NR: Number of blocks per side of the matrix NNZB: Number of Non-Zero Blocks NB: Number of elements per side of the Block N: Number of elements per side of the matrix

Preconditioners n n n Incomplete LU factorization Jacobi, Gauss-Seidel, SOR Schwarz; within blocks use LU, ILU, SOR, etc.

Solvers n n Direct method (LU) Krylov method (CG, GMRES, Bi. CGstab, CGS, QMR, …) Non-Krylov iterative method (Jacobi, G-S, SOR) Pre-conditioned Krylov method

Interface to external solver Both Iterative and Director solvers n AMG n Block. Solve 95 n LUSOL n SPAI n Super. LU

Functions n n Define the linear system (Ax=b) Mat. Create(), Mat. Set. Value(), Vec. Create() Create the Solver SLESCreate(), SLESSet. Operators() Solve System of Equations SLESSolve() Clean up SLESDestroy()

Example n n Solve Ax = b www. cs. ucsb. edu/~jh/example. cc
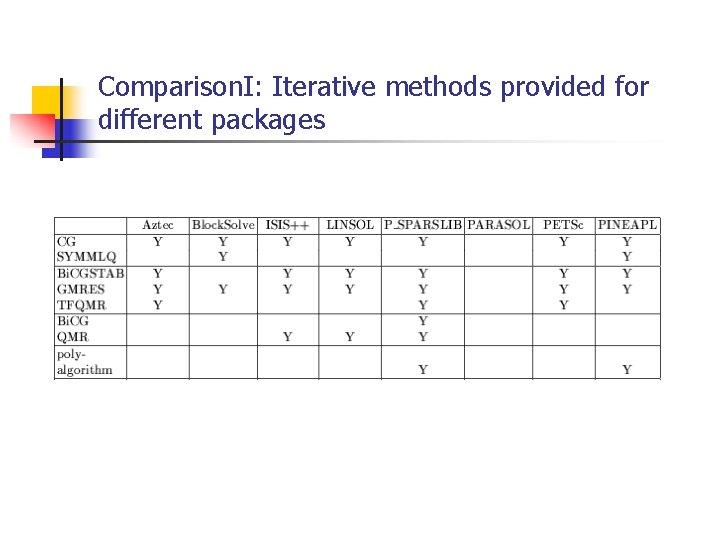
Comparison. I: Iterative methods provided for different packages
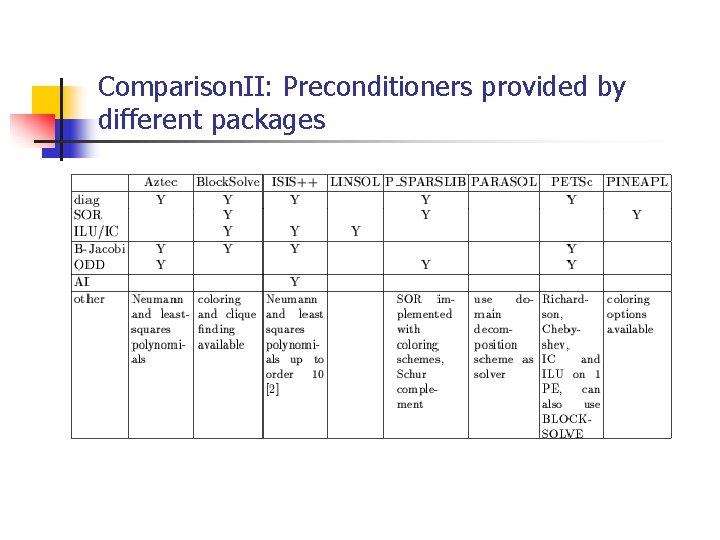
Comparison. II: Preconditioners provided by different packages
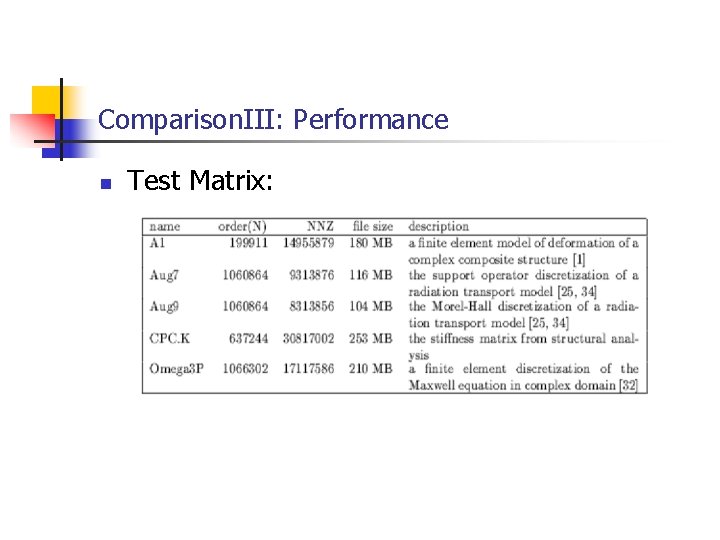
Comparison. III: Performance n Test Matrix:

Comparison. III: Performance n n Feed these matrices to Aztec and PETSc Generate a zero vector as initial guess and a vector of 1 as RHS Use GMRES without preconditoners, max iteration = 500 Run on 512 -processor Cray T 3 E 900
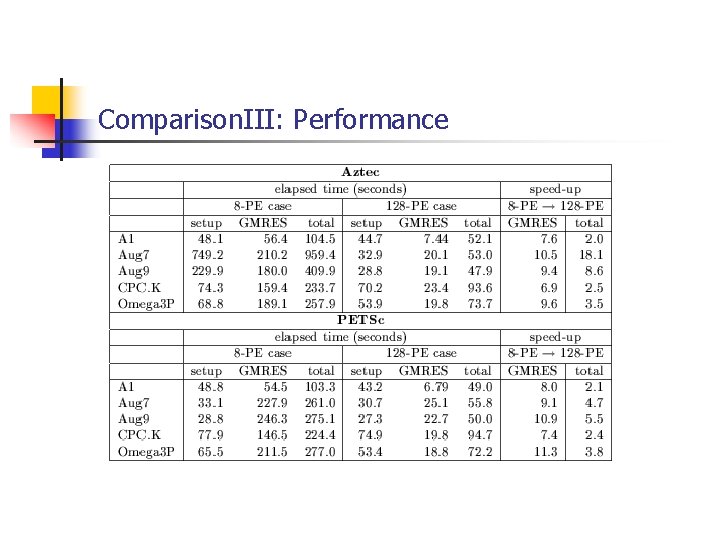
Comparison. III: Performance
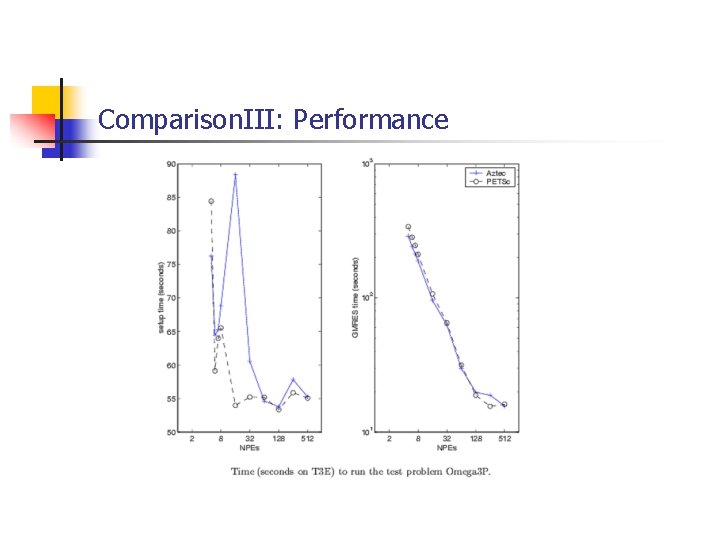
Comparison. III: Performance

Comparison. III: Performance n n Aztect suffers from setup varization PETSc did not optimize partition algorithm( PE 256 -> PE 512, performance decrease). Communication takes more time than computation

Conclusion n PETSc - Well designed and widely used - First MPI-based program to public Good set of iterative methods and preconditioners Good Support and excellent technical documents Still under developement

Thanks Comments ?
- Slides: 29