Petri Net Abstract formal model of information flow

Petri Net : Abstract formal model of information flow Major use: Modeling of systems of events in which it is possible for some events to occur concurrently, but there are constraints on the occurrences, precedence, or frequency of these occurrences. Petri Net 1

Petri Net as a Graph : Models static properties of a system • Graph contains 2 types of nodes – Circles (Places) – Bars (Transitions) • Petri net has dynamic properties that result from its execution – Markers (Tokens) – Tokens are moved by the firing of transitions of the net. Petri Net 2

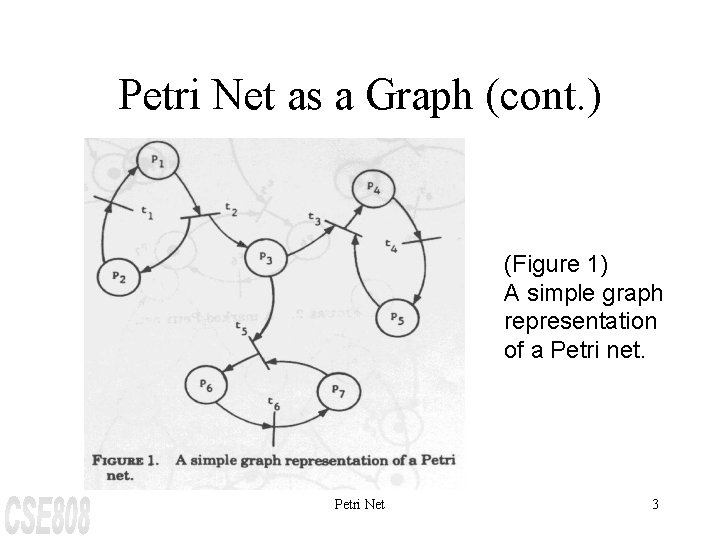
Petri Net as a Graph (cont. ) (Figure 1) A simple graph representation of a Petri net. Petri Net 3

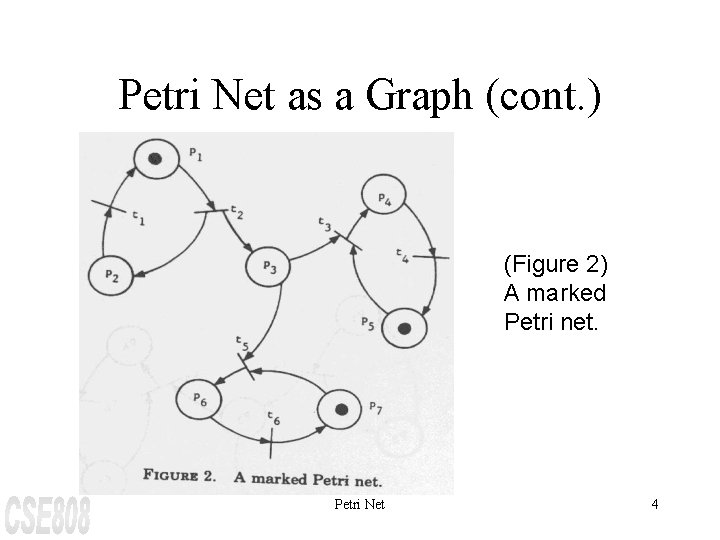
Petri Net as a Graph (cont. ) (Figure 2) A marked Petri net. Petri Net 4

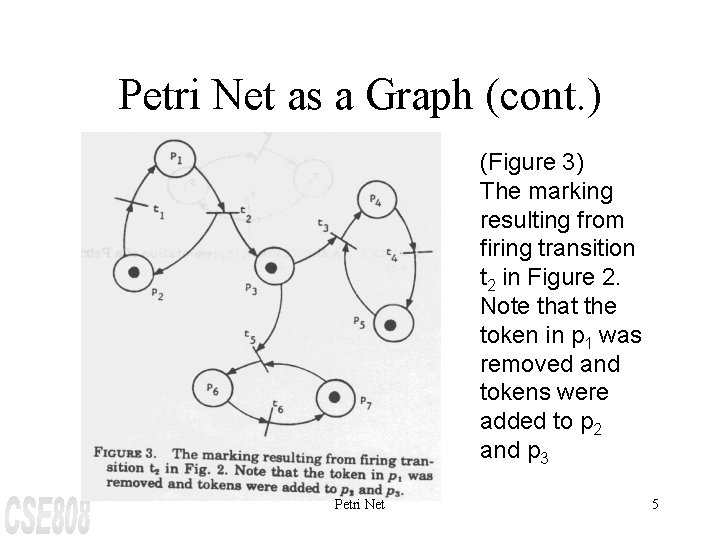
Petri Net as a Graph (cont. ) (Figure 3) The marking resulting from firing transition t 2 in Figure 2. Note that the token in p 1 was removed and tokens were added to p 2 and p 3 Petri Net 5

Petri Net as a Graph (cont. ) (Figure 4) Markings resulting from the firing of different transitions in the net of Figure 3. (a) Result of firing transition t 1 Petri Net 6

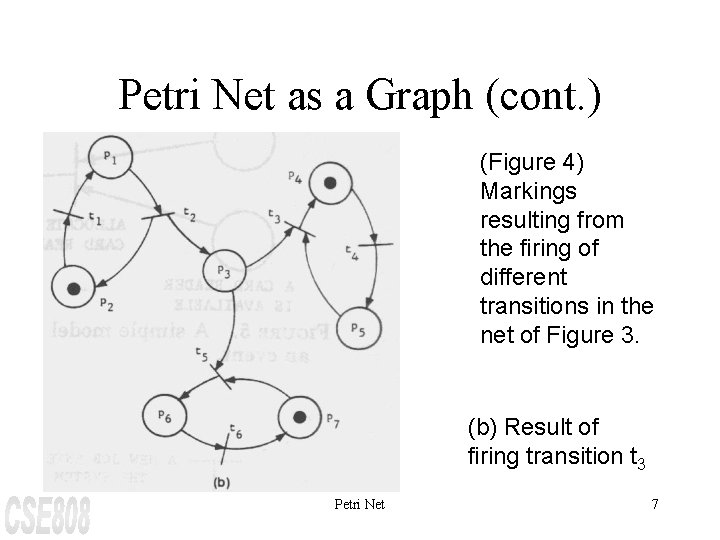
Petri Net as a Graph (cont. ) (Figure 4) Markings resulting from the firing of different transitions in the net of Figure 3. (b) Result of firing transition t 3 Petri Net 7

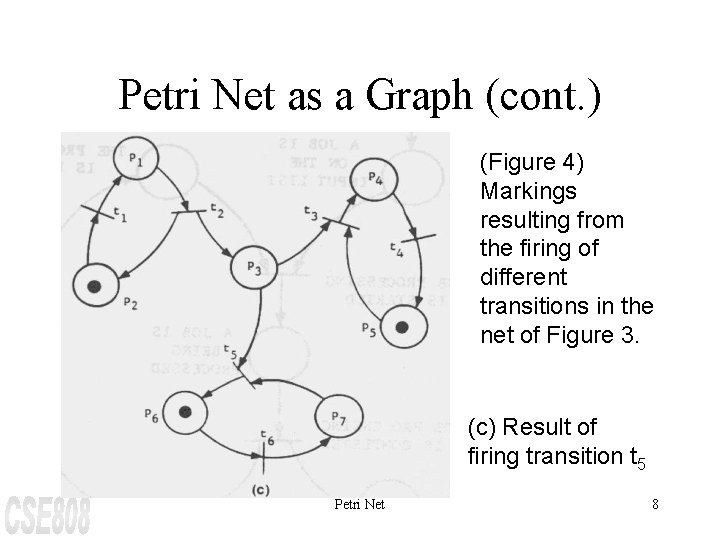
Petri Net as a Graph (cont. ) (Figure 4) Markings resulting from the firing of different transitions in the net of Figure 3. (c) Result of firing transition t 5 Petri Net 8

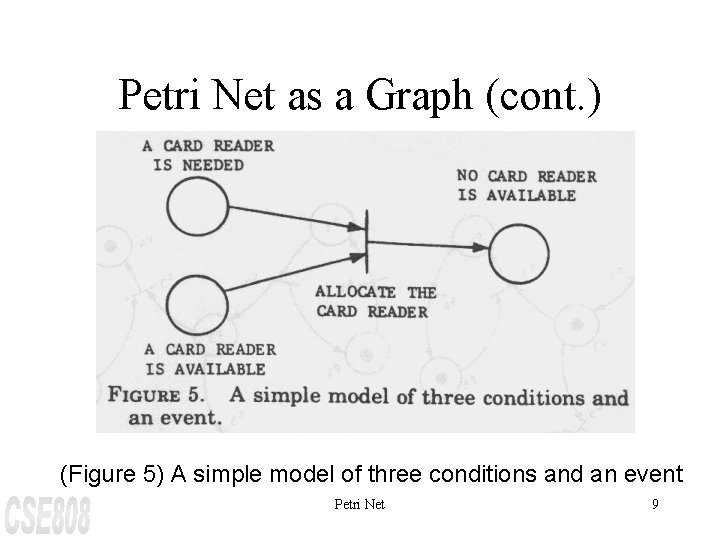
Petri Net as a Graph (cont. ) (Figure 5) A simple model of three conditions and an event Petri Net 9

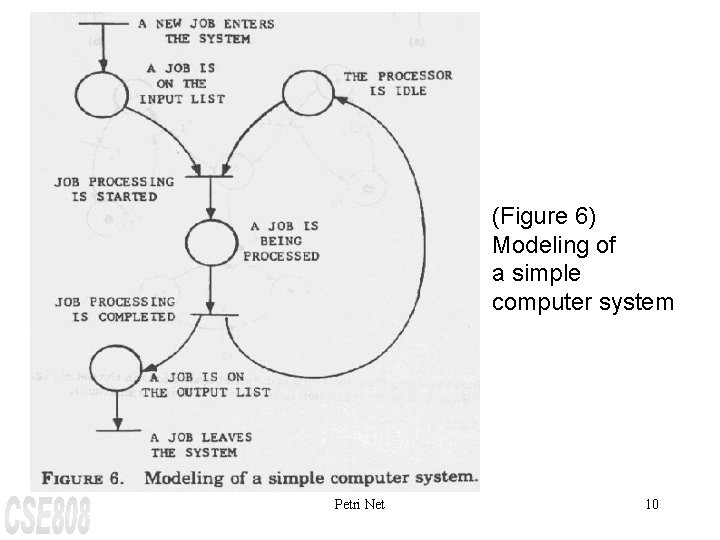
(Figure 6) Modeling of a simple computer system Petri Net 10

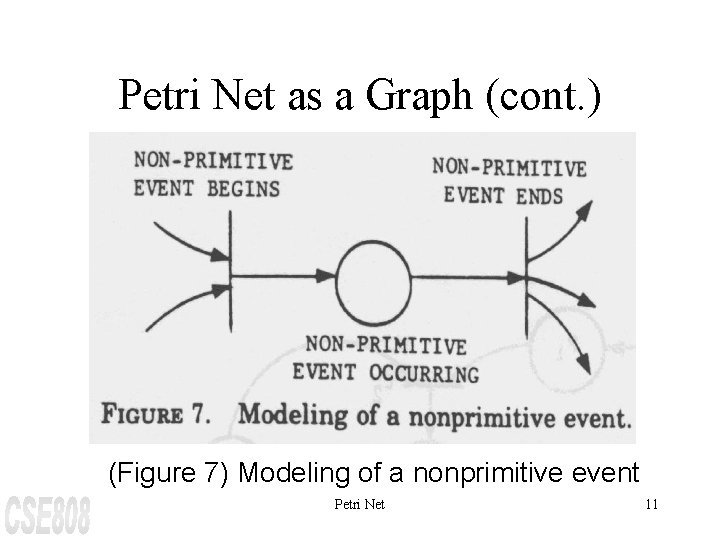
Petri Net as a Graph (cont. ) (Figure 7) Modeling of a nonprimitive event Petri Net 11

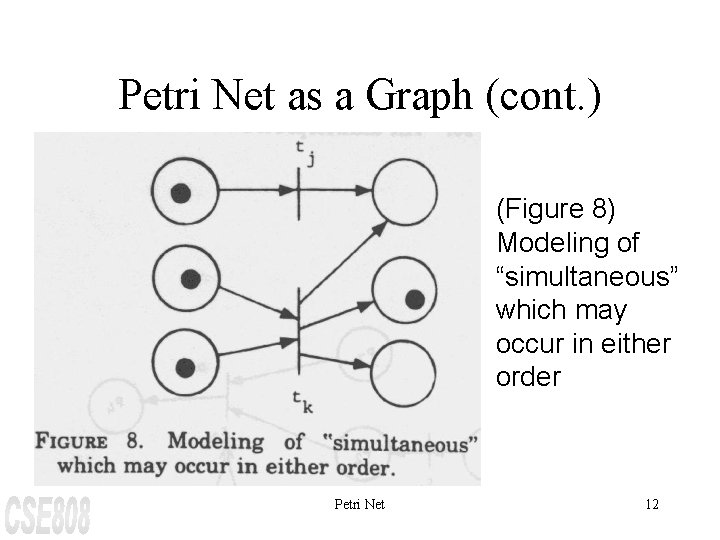
Petri Net as a Graph (cont. ) (Figure 8) Modeling of “simultaneous” which may occur in either order Petri Net 12

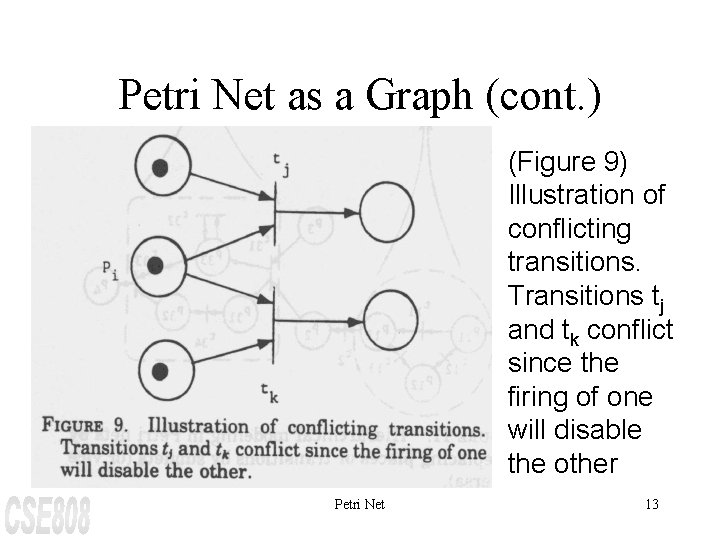
Petri Net as a Graph (cont. ) (Figure 9) Illustration of conflicting transitions. Transitions tj and tk conflict since the firing of one will disable the other Petri Net 13

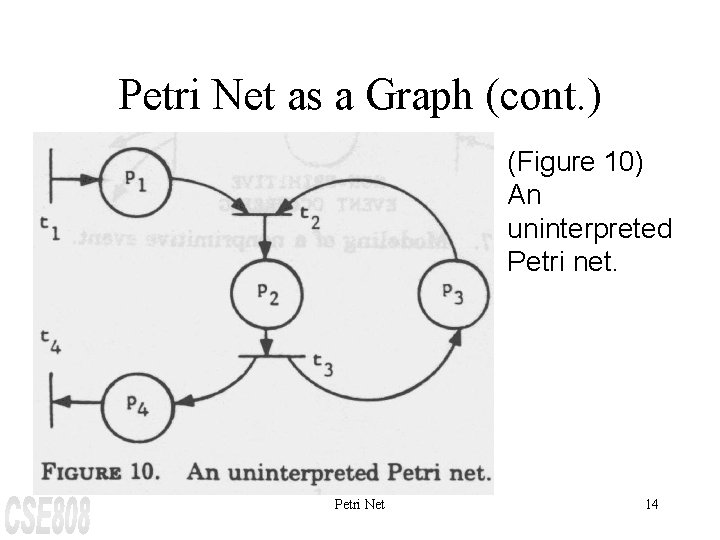
Petri Net as a Graph (cont. ) (Figure 10) An uninterpreted Petri net. Petri Net 14

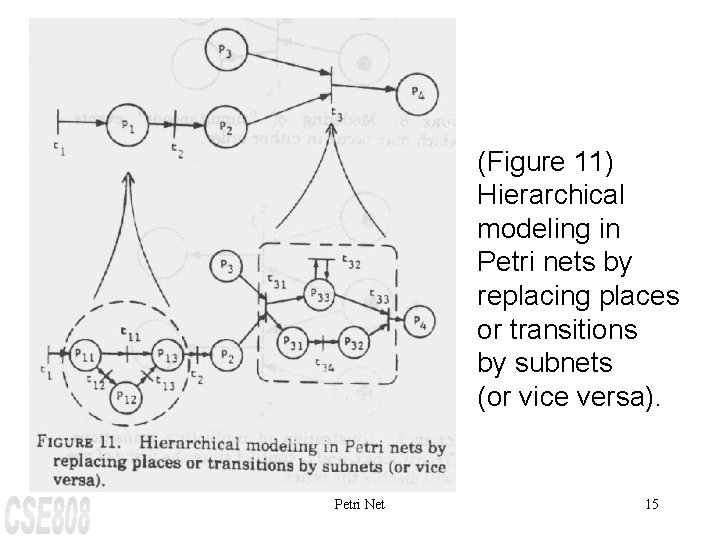
(Figure 11) Hierarchical modeling in Petri nets by replacing places or transitions by subnets (or vice versa). Petri Net 15

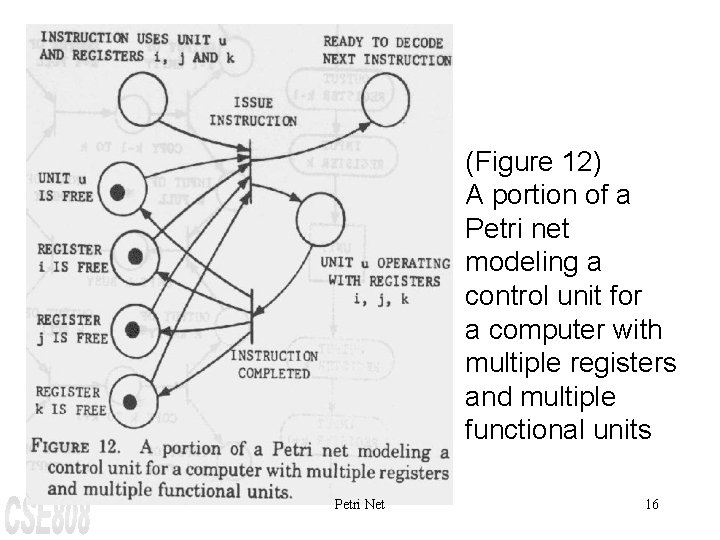
(Figure 12) A portion of a Petri net modeling a control unit for a computer with multiple registers and multiple functional units Petri Net 16

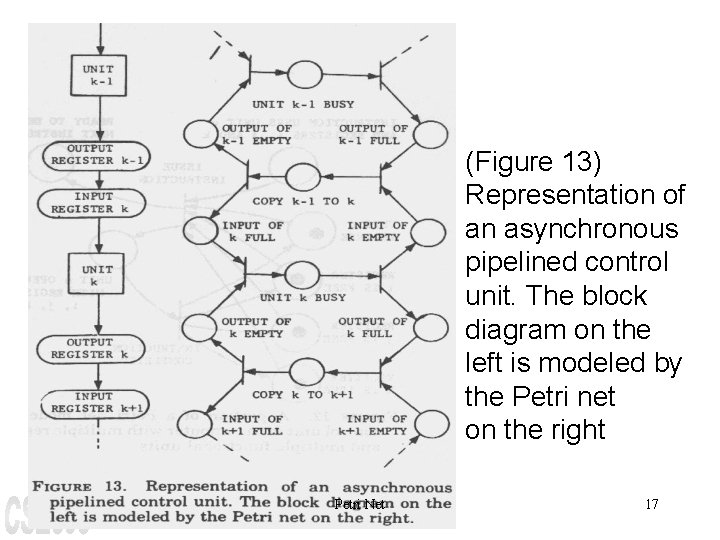
(Figure 13) Representation of an asynchronous pipelined control unit. The block diagram on the left is modeled by the Petri net on the right Petri Net 17

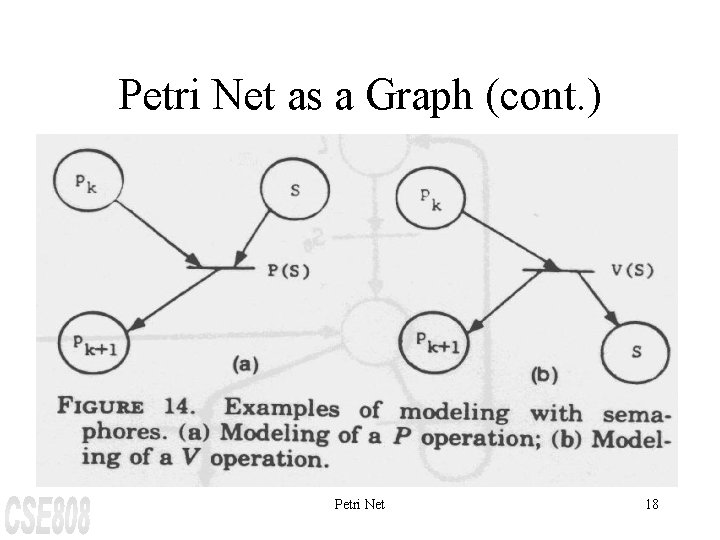
Petri Net as a Graph (cont. ) Petri Net 18

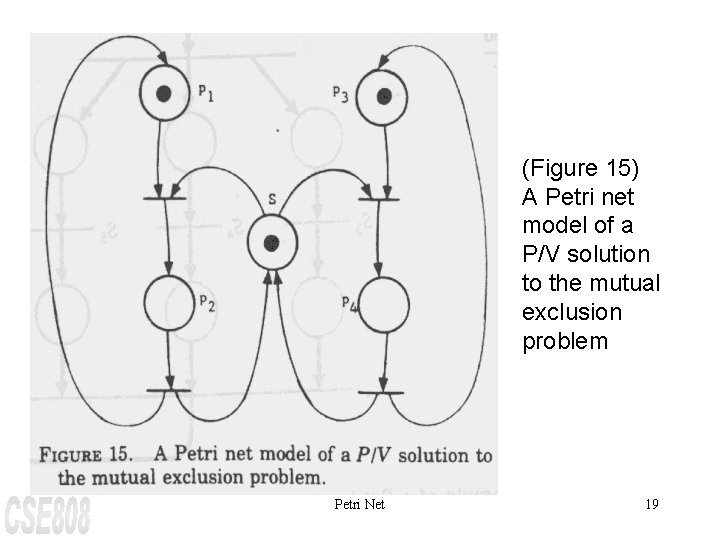
(Figure 15) A Petri net model of a P/V solution to the mutual exclusion problem Petri Net 19

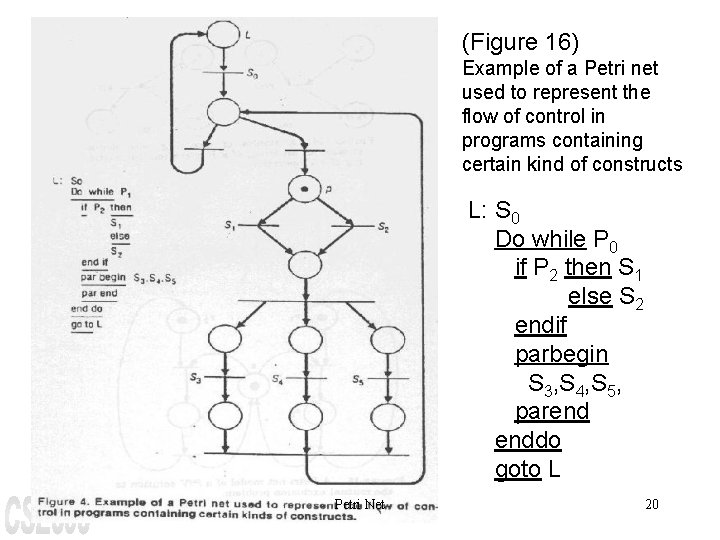
(Figure 16) Example of a Petri net used to represent the flow of control in programs containing certain kind of constructs L: S 0 Do while P 0 if P 2 then S 1 else S 2 endif parbegin S 3, S 4, S 5, parend enddo goto L Petri Net 20

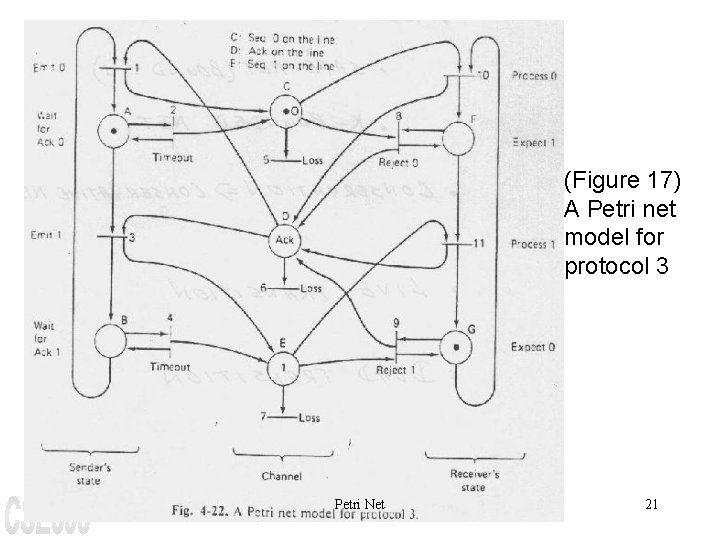
(Figure 17) A Petri net model for protocol 3 Petri Net 21

Other properties for analysis • Boundeness – Safe net (bound = 1) – K-bounded net • Conservation ==> conservative net • Live transition • Dead transition Petri Net 22

State of a Petri net • State - defined by its marking, m • State space - set of all markings: (m 0, m 1, m 2, . . . ) • Change in state - caused by firing a transition, defined by partial Fn, d (example) m 1 = d (m 0 , tj) • Note: marking -For a marking m , m(Pi) = mi A marked Petri net: m = (P, T, I, O, m) Petri Net 23

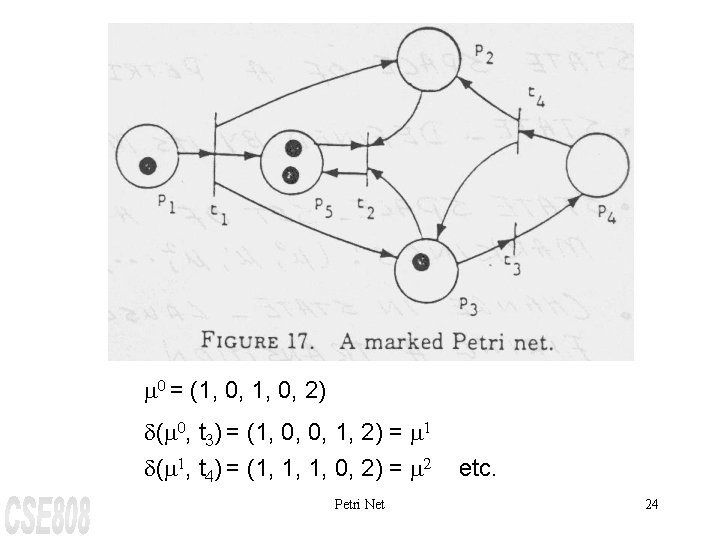
m 0 = (1, 0, 2) d(m 0, t 3) = (1, 0, 0, 1, 2) = m 1 d(m 1, t 4) = (1, 1, 1, 0, 2) = m 2 Petri Net etc. 24

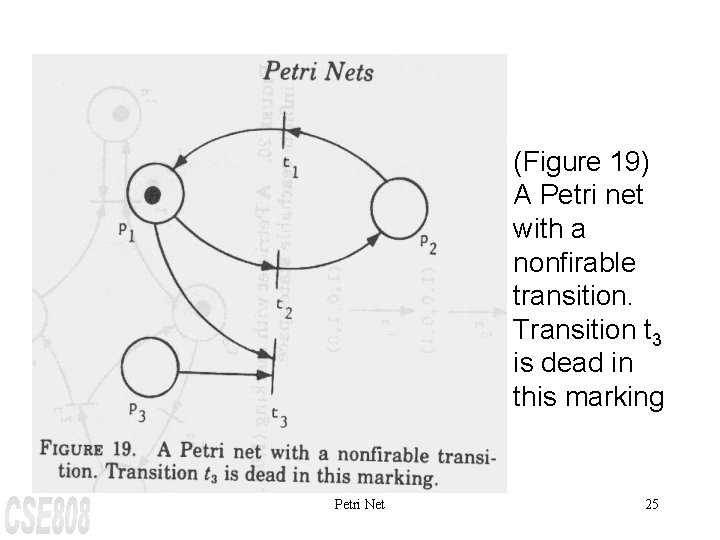
(Figure 19) A Petri net with a nonfirable transition. Transition t 3 is dead in this marking Petri Net 25

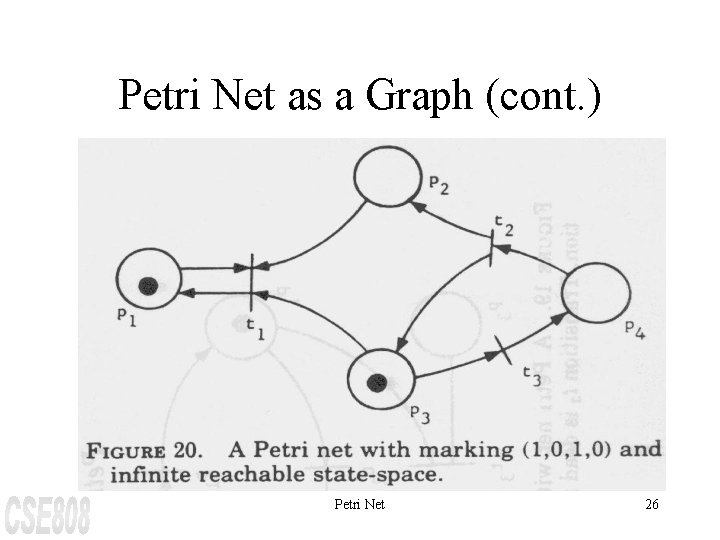
Petri Net as a Graph (cont. ) Petri Net 26

Petri Net as a Graph (cont. ) (1, 0, 1, 0) (Figure 21) The reachability tree of the Petri net of Figure 19 t 3 (1, 0, 0, 1) t 2 (1, w, 1, 0) t 1 (1, w, 0, 0) t 3 (1, w, 0, 1) t 2 (1, w, 1, 0) Petri Net 27

Unsolvable Problems • Subset problem - given 2 marked Petri nets, is the reachability of one net a subset of the reachability of the other net undecidable (Hack). . . • Complexity reachability problem is exponential time-hard and exponential space-hard. Petri Net 28