Peta Kendali Atribut Dani Leonidas S MT Peta

Peta Kendali Atribut Dani Leonidas S, MT

Peta Kendali Atribut Peta kendali atribut menggolongkan setiap butir yang diperiksa termasuk ke dalam kategori sesuai atau tidak sesuai dengan spesifikasi. Spesifikasi ditentukan berdasarkan karakteristik yang tak bisa diukur.

Jenis Peta Kendali Atribut Jenis peta kendali atribut: 1. Peta p bagian/proporsi produk yang tak sesuai spesifikasi. 2. Peta np jumlah produk yang tak sesuai spesifikasi. 3. Peta c jumlah ketidaksesuaian pada produk. 4. Peta u jumlah ketidaksesuaian pada produk per satuan.

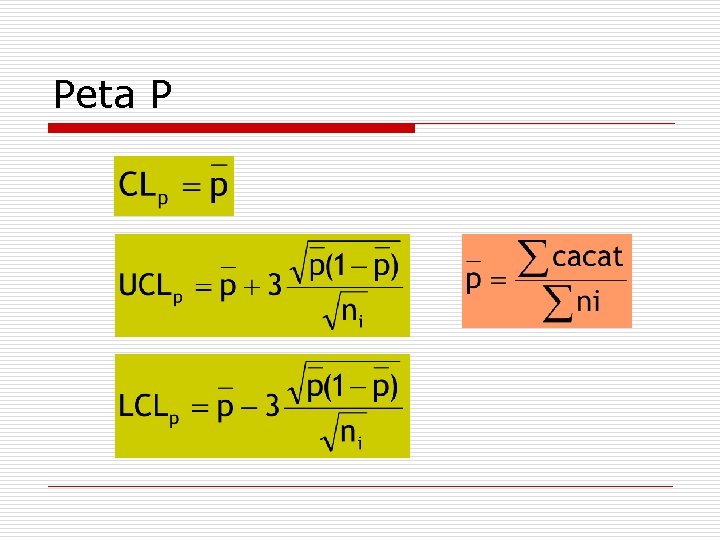
Peta P

PETA p (2) Peta p Untuk Ukuran Sampel Sama Peta p Untuk Ukuran Sampel Berbeda Peta p Berdasarkan Ukuran Rata-rata Sub Grup Peta p dengan p standard / diketahui dari penelitian sebelumnya

Peta p Untuk Ukuran Sampel Sama o - Diketahui 100 unit diperiksa setiap hari untuk produk sinar katode. Setelah 21 hari, didapat Σp = 5, 46. Hitung batas-batas kendali 3σ untuk bagan p

Jawab o Σp = 5, 46 p rata-rata = 5, 46/21 = 0, 26

Soal (peta p ukuran sampel berbeda) o Pemeriksaan 100% dilakukan terhadap sejenis produk tertentu segera setelah produk tersebut dibuat, dan datanya diringkas untuk setiap jam. Hitung batas-batas kendali yang berubah-ubah untuk bagan p

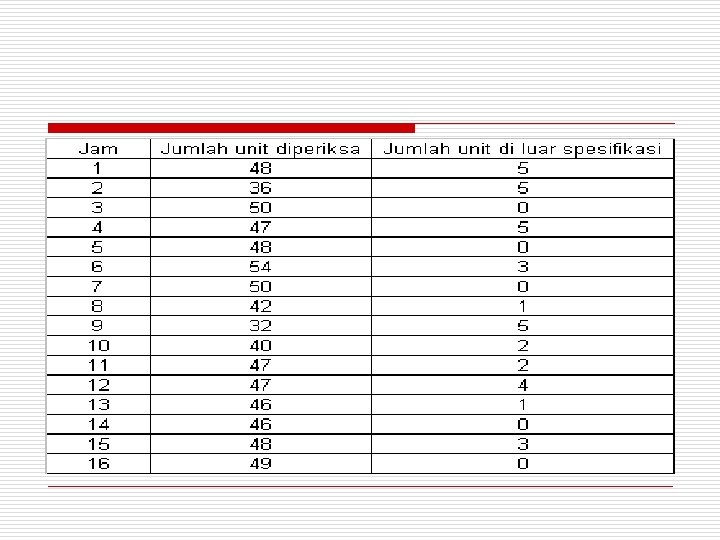
Jawab o - Σp= 730 p; Σnp= 36 rata-rata p = 36/730 = 0, 049

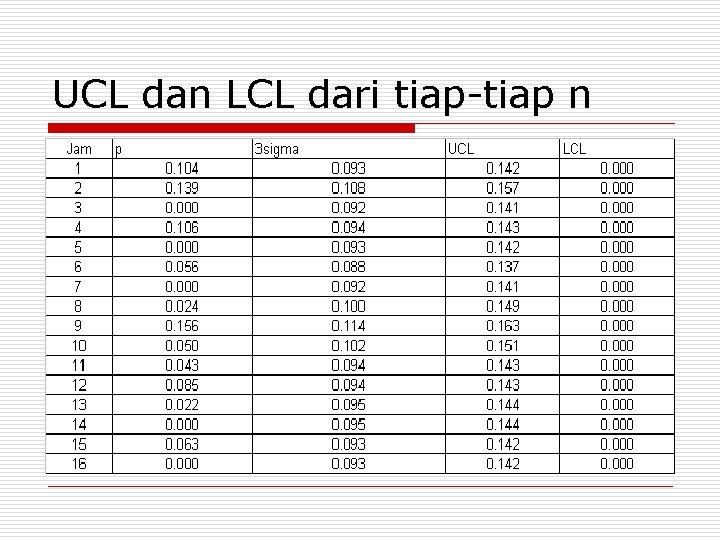
UCL dan LCL dari tiap-tiap n

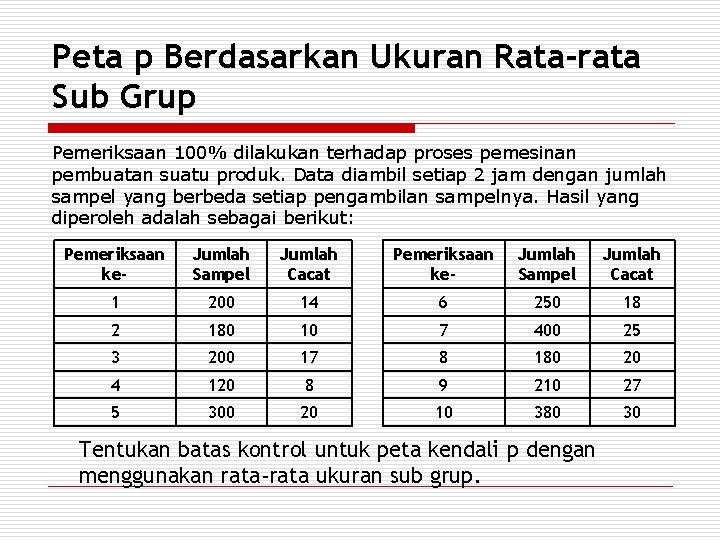
Peta p Berdasarkan Ukuran Rata-rata Sub Grup Pemeriksaan 100% dilakukan terhadap proses pemesinan pembuatan suatu produk. Data diambil setiap 2 jam dengan jumlah sampel yang berbeda setiap pengambilan sampelnya. Hasil yang diperoleh adalah sebagai berikut: Pemeriksaan ke- Jumlah Sampel Jumlah Cacat 1 200 14 6 250 18 2 180 10 7 400 25 3 200 17 8 180 20 4 120 8 9 210 27 5 300 20 10 380 30 Tentukan batas kontrol untuk peta kendali p dengan menggunakan rata-rata ukuran sub grup.

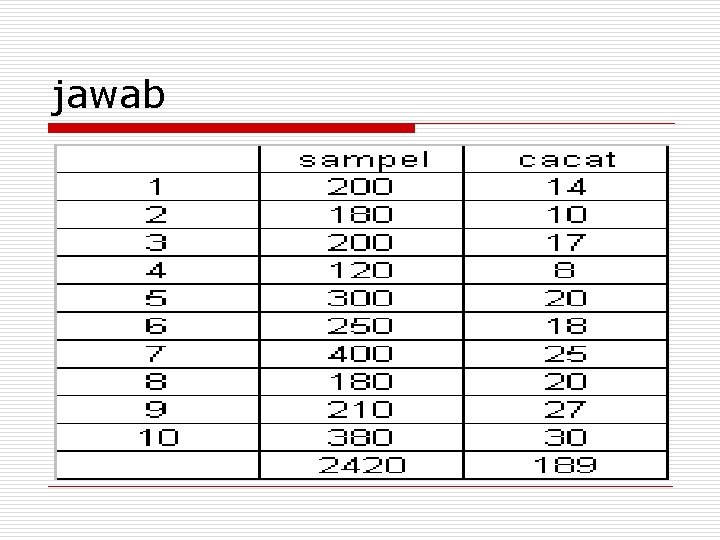
jawab

o o P rata-rata = 189/2420 = 0, 078 n rata-rata = 2420/10 = 242 UCLp = 0, 078 + 3σp = 0, 078+0, 052 = 0, 13 LCL = 0, 078 -0, 052 = 0, 026

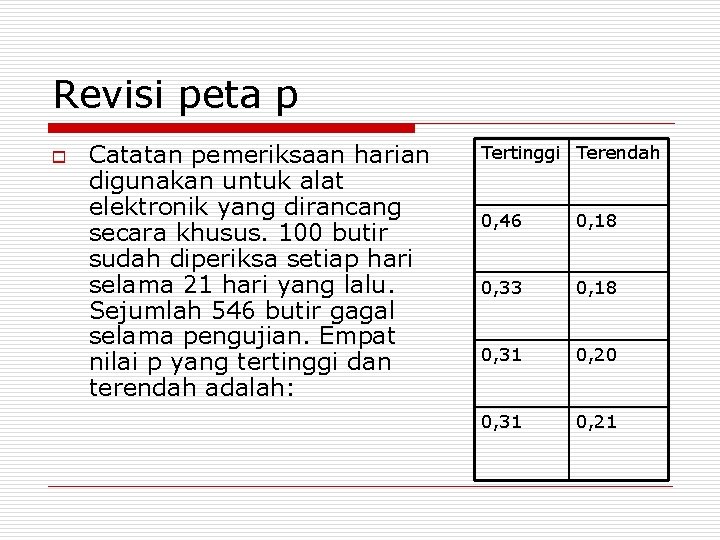
Revisi peta p o Catatan pemeriksaan harian digunakan untuk alat elektronik yang dirancang secara khusus. 100 butir sudah diperiksa setiap hari selama 21 hari yang lalu. Sejumlah 546 butir gagal selama pengujian. Empat nilai p yang tertinggi dan terendah adalah: Tertinggi Terendah 0, 46 0, 18 0, 33 0, 18 0, 31 0, 20 0, 31 0, 21

o o Hitung garis pusat dan batas-batas kendali percobaan 3σ untuk bagan p. Dalam keadaan terkendalikah operasi proses ini? Rekomendasikan nilai po sasaran dan batas-batas kendali 3σ untuk penggunaan bagan p secara kontinu

o o o P rata-rata = 546/(21 x 100) = 0, 26 UCL = 0, 26 + 0, 132 = 0, 392 LCL = 0, 26 – 0, 132 =0, 128

o o Ada satu titik berada di luar batas kendali, yaitu titik dengan p= 0, 46 P baru = (546 – 46 ) / (2100 – 100) = 0, 25

o o UCLp = p + 3σ = 0, 25 + 0, 130 = 0, 380 LCLp = p - 3σ = 0, 25 – 0, 130 = 0, 120

Peta np o o Jumlah produk yang tidak sesuai yang ditemukan dalam pemeriksaan atau sederetan pemeriksaan terhadap total barang yang benar-benar diperiksa. Digunakan hanya untuk ukuran sample yang sama

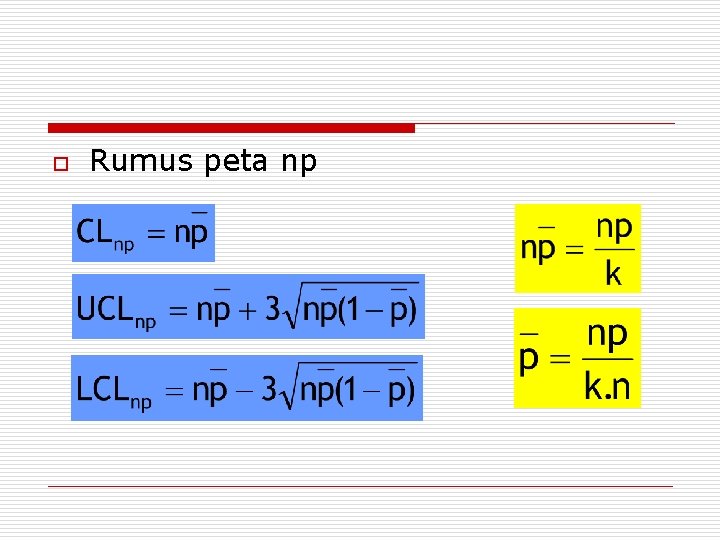
o Rumus peta np

Contoh soal o Sebuah pemeriksaan pada komponen logam lembaran ukuran lot 200 menghasilkan data seperti tabel berikut. Anda diminta untuk membuat peta kendali np

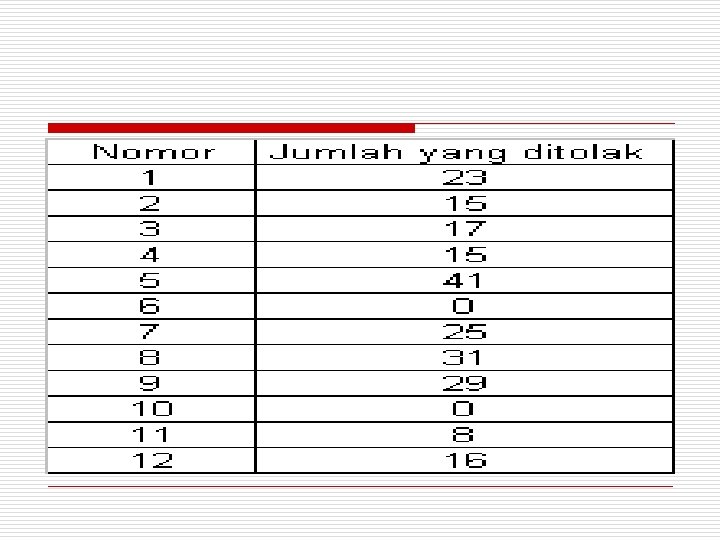
UCL = 18, 3 + 12, 2 = 30, 5 LCL = 18, 3 – 12, 2 = 6, 1

Penggunaan tabel G o Tabel G digunakan untuk mengetahui probabilitas dari terdapatnya jumlah cacat tertentu pada suatu rata-rata proses.

o - - Sejumlah 750 butir ditemukan tidak memenuhi spesifikasi dalam 50 lot pertama dari butir baru yang diproduksi dalam lotlot berukuran 500 unit. Hitung batas-batas kendali untuk bagan np Jika rata-rata proses tetap, Berapa probabilitas bahwa lot ke 51 akan berisi lebih dari 20 unit yang tak sesuai? Jika rata-rata proses naik 5, berapa probabilitas bahwa ke lot 51 akan berisi tepat 25 unit yang tak sesuai?

Batas kendali bagan np

Probabilitas bahwa lot ke 51 akan berisi lebih dari 20 unit yang tak sesuai

rata-rata proses naik 5, probabilitas bahwa ke lot 51 akan berisi tepat 25 unit yang tak sesuai

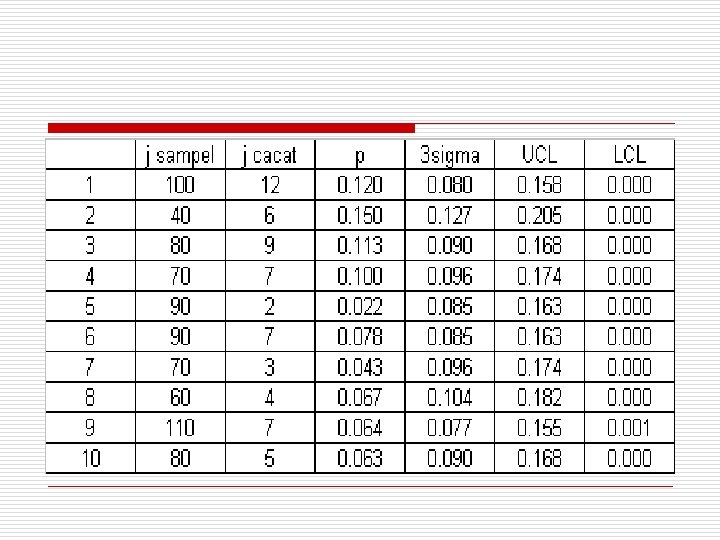
Latihan Pemeriksaan 100% dilakukan terhadap proses bubut pembuatan suatu produk. Data diambil 10 kali dengan hasil sebagai berikut: Pemeriksaan ke- Jumlah Sampel Jumlah Cacat 1 100 12 6 90 7 2 40 6 7 70 3 3 80 9 8 60 4 4 70 7 9 110 7 5 90 2 10 80 5 Tentukan batas kontrol untuk peta kendali p untuk setiap pemeriksaan. Bila ada data yang berada di luar batas kontrol lakukan revisi.

Jawab o - Σp= 790 p; Σnp= 62 rata-rata p = 62/790 = 0, 078

Perbedaan antara Barang yang tak sesuai dan ketaksesuaian o o Barang yang tak sesuai (cacat) = barang yang dalam beberapa hal gagal memenuhi satu atau lebih spesifikasi yang ditetapkan Ketaksesuaian =setiap kejadian dari kurangnya kesesuaian barang terhadap spesifikasi Setiap barang yang tak sesuai berisi satu atau lebih ketaksesuaian. Bagan c berlaku bagi sejumlah ketaksesuaian dalam sub grup berukuran konstan

Bagan c o o o Bagan c berlaku bagi sejumlah ketaksesuaian dalam sub grup berukuran konstan Peubah c adalah jumlah ketaksesuaian yang diamati dalam satu barang Namun bagan sub grup bagan c dapat terdiri dari 2 atau lebih barang, namun jumlahnya konstan

Bagan C o Bagan c berlaku bagi sejumlah ketidaksesuaian dalam sub group yang berukuran konstan

Contoh Soal (8) Tabel berikut ini menunjukkan jumlah ketidaksesuaian pada sebuah produk otomotif. No Jumlah Ketidaksesuaian 1 9 6 2 11 11 16 5 2 6 7 9 12 7 17 4 3 4 8 7 13 6 18 9 4 3 9 6 14 15 19 11 5 5 10 4 15 6 20 7 Tentukan batas-batas kendali hasil pemeriksaan di atas dan berapa nilai c 0 yang diusulkan untuk pemeriksaan berikutnya ?

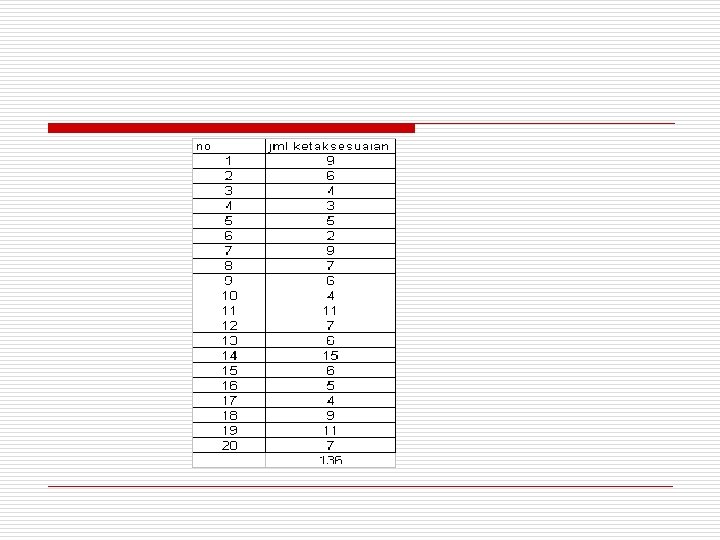
Batas kendali

o Sampel nomor 14 diatas UCL

Penggunaan tabel G o Tabel G juga digunakan untuk mengetahui probabilitas dari terdapatnya jumlah ketaksesuaian tertentu pada suatu rata-rata proses.

Peta u ketidaksesuaian per unit o Peta u berlaku bagi sejumlah ketidaksesuaian dalam sub group yang berukuran berbeda-beda.

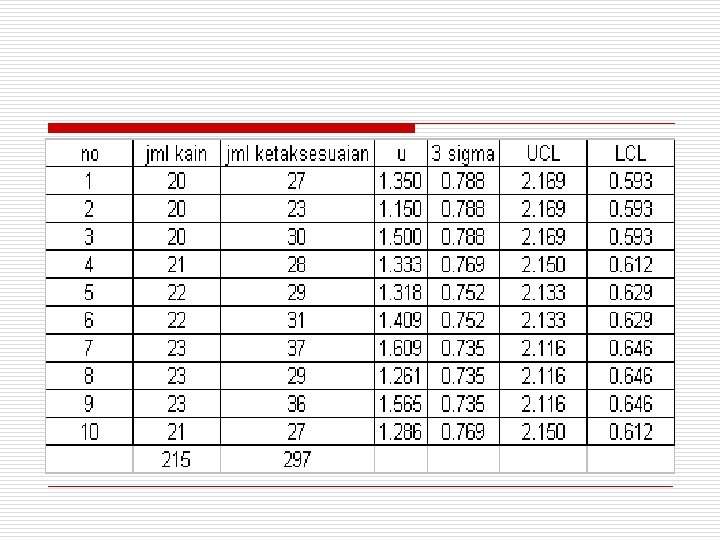
Contoh Soal Pada tabel berikut ini dicatat jumlah kain yang diproduksi per hari (satuan gulung). Gunakan data ini untuk menduga µ 0 dan hitung batas kendali pada bagan u. No Jumlah Kain Ketaksempurnaan 1 20 27 6 22 31 2 20 23 7 23 37 3 20 30 8 23 29 4 21 28 9 23 36 5 22 29 10 21 27