Pesquisa Operacional I Fundamentos Marcone Jamilson Freitas Souza

Pesquisa Operacional I Fundamentos Marcone Jamilson Freitas Souza Alexandre Xavier Martins Tatiana Alves Costa José Maria do Carmo Bento Alves Frederico Augusto Coimbra Guimarães Departamento de Computação Programa de Pós-Graduação em Engenharia Mineral Universidade Federal de Ouro Preto http: //www. iceb. ufop. br/prof/marcone

Roteiro l l l l Solução gráfica de um PPL Teorema Fundamental da Programação Linear Caracterização de vértice Fundamentação do Método SIMPLEX Método das duas fases Dualidade Análise de sensibilidade

Resolução gráfica de PPL’s Passos para resolver graficamente um PPL: l a) b) c) d) e) Escolher uma solução x viável qualquer Traçar o hiperplano definido pela função objetivo passando pelo ponto x Determinar o gradiente da função objetivo no ponto x Caminhar no sentido e direção do gradiente da função objetivo até tangenciar a região viável O ponto de tangência representa a solução ótima x*

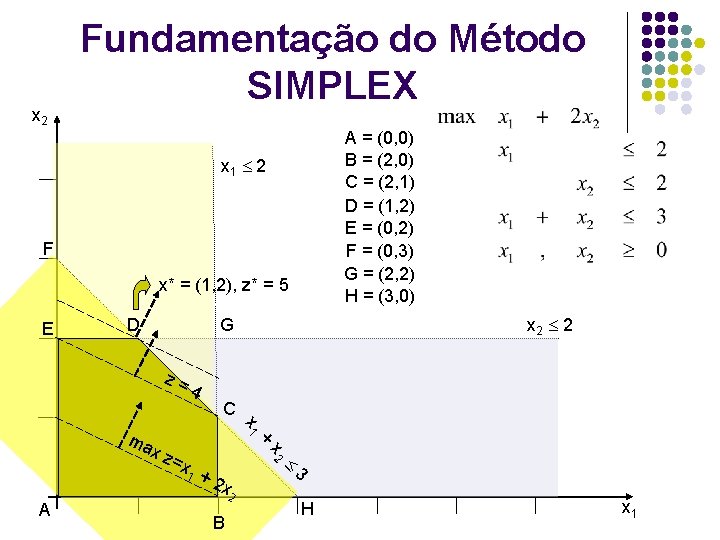
Fundamentação do Método SIMPLEX Seja resolver o seguinte PPL:

x 2 Fundamentação do Método SIMPLEX A = (0, 0) B = (2, 0) C = (2, 1) D = (1, 2) E = (0, 2) F = (0, 3) G = (2, 2) H = (3, 0) x 1 2 F x* = (1, 2), z* = 5 E z= 4 + B 3 +2 x 2 =x x 2 xz 1 A C x 1 ma x 2 2 G D H x 1

Teorema Fundamental da Programação Linear O ótimo de um PPL, se existir, ocorre em pelo menos um vértice do conjunto de soluções viáveis. Situações que podem ocorrer com relação ao conjunto M de soluções viáveis: l l 1) M = {} Neste caso não há solução viável => Não há solução ótima

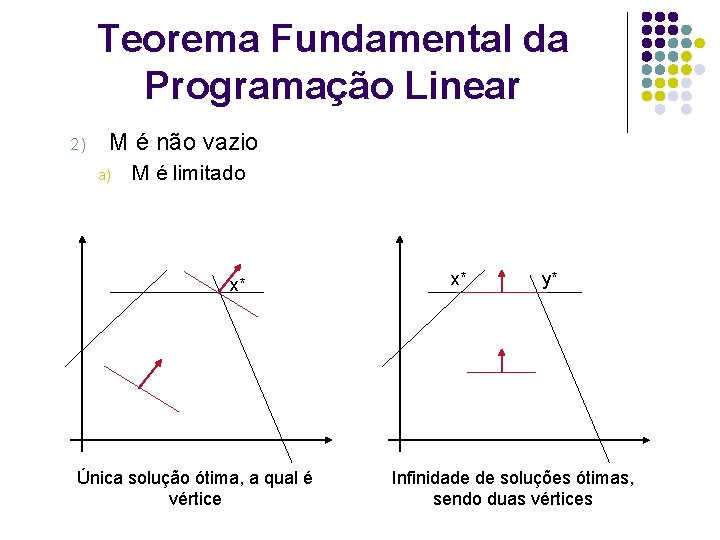
Teorema Fundamental da Programação Linear 2) M é não vazio a) M é limitado x* Única solução ótima, a qual é vértice x* y* Infinidade de soluções ótimas, sendo duas vértices

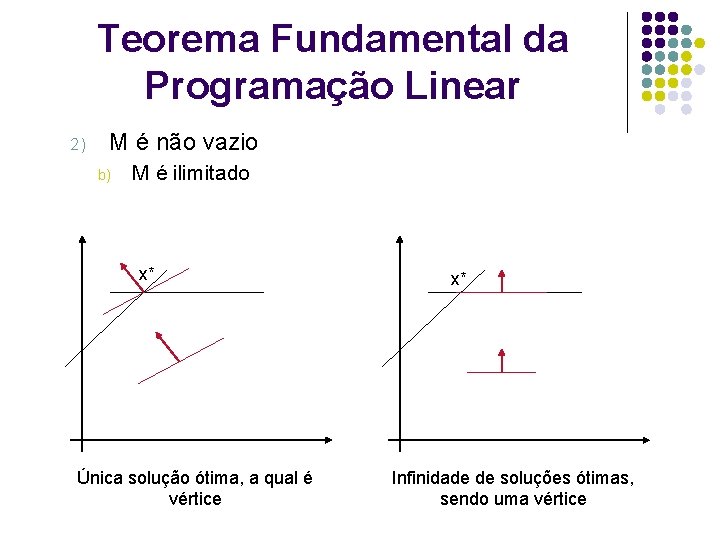
Teorema Fundamental da Programação Linear 2) M é não vazio b) M é ilimitado x* Única solução ótima, a qual é vértice x* Infinidade de soluções ótimas, sendo uma vértice

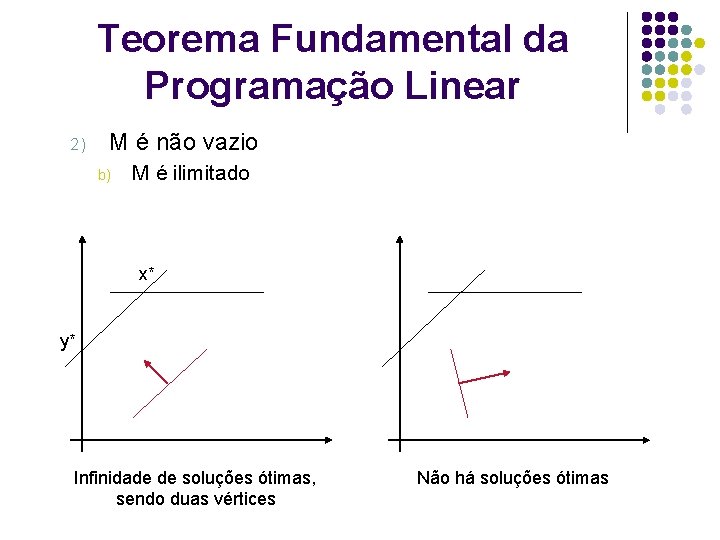
Teorema Fundamental da Programação Linear 2) M é não vazio b) M é ilimitado x* y* Infinidade de soluções ótimas, sendo duas vértices Não há soluções ótimas

Forma-padrão de um PPL l PPL está na forma-padrão quando é posto na forma: sendo

Redução de um PPL qualquer à forma-padrão l Restrições do tipo x 3 0 l Restrições do tipo x 4 0

Redução de um PPL qualquer à forma-padrão l Existe bi < 0 Solução: Basta multiplicar restrição i por -1 l Existem variáveis não-positivas Seja xk 0: Solução: Criar variável xk’ tal que xk’ = - xk Assim, modelo terá variável xk’ 0

Redução de um PPL qualquer à forma-padrão l Existem variáveis livres, isto é, variáveis xk que podem assumir qualquer valor real (negativo, nulo ou positivo) Solução: Substituir xk por xk’ – xk’’ , com xk’ 0 e xk’’ 0 xk’ > xk’’ xk > 0 xk’ = xk’’ xk = 0 xk’ < xk’’ xk < 0 l PPL é de maximização: max f(x) = - min {-f(x)}

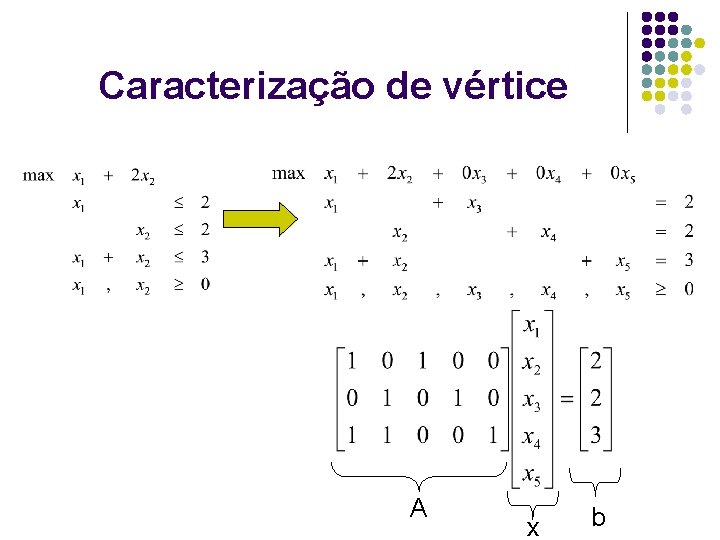
Caracterização de vértice A x b

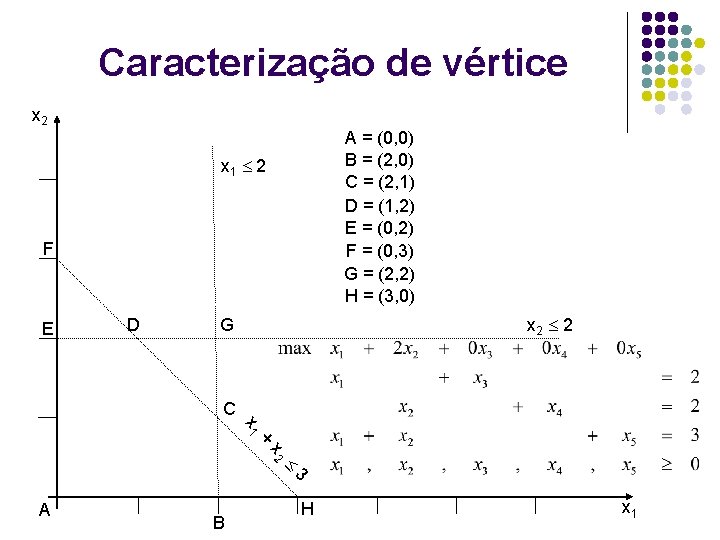
Caracterização de vértice x 2 A = (0, 0) B = (2, 0) C = (2, 1) D = (1, 2) E = (0, 2) F = (0, 3) G = (2, 2) H = (3, 0) x 1 2 F E D x 2 2 G C x 1 + x 2 3 A B H x 1

Caracterização de vértice l l l Em um ponto no interior do conjunto (não pertencente a nenhuma aresta) não há variáveis nulas Em uma aresta há, pelo menos, uma variável nula Em um vértice há, pelo menos, n-m variáveis nulas n-m m R B n m

Caracterização de vértice l Para gerar um vértice: l l Escolher uma matriz não-singular B tal que: Bx. B + Rx. R = b Fazer x. R = 0 Se ao resolver o sistema Bx. B = b, for obtido x. B 0, então x = (x. B x. R)t = (x. B 0)t é vértice Deste procedimento resulta uma Solução Básica Viável (SBV), com o significado geométrico de vértice.

Definições l l l B = base x. B = vetor das variáveis básicas x. R = vetor das variáveis não-básicas Solução Básica (SB) = vetor x tal que Bx. B=b e x. R = 0 Solução Básica Viável (SBV) = vetor x tal que Bx. B=b; x. B 0 e x. R = 0 Solução Básica Viável Degenerada (SBVD) = SBV em que existe variável básica nula

Princípio de funcionamento do Algoritmo SIMPLEX SBV inicial Esta SBV pode ser melhorada? Sim Determine VNB que deve entrar na base Determine VB que deve deixar a base Encontre nova SBV Não Pare: Esta SBV é ótima

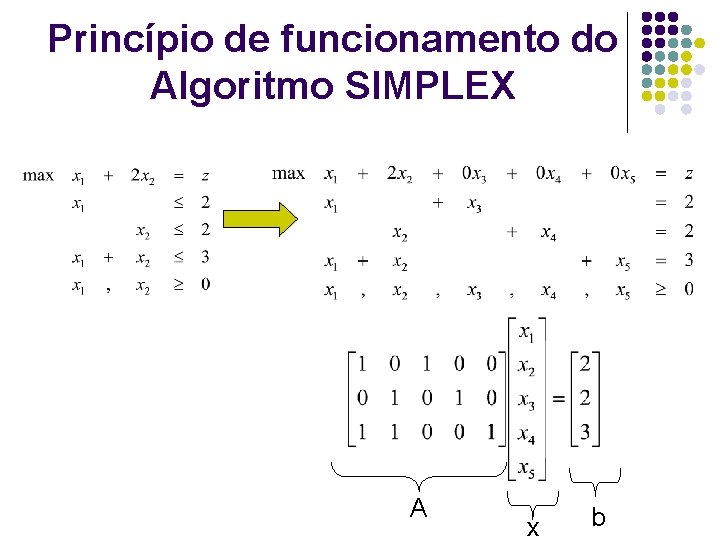
Princípio de funcionamento do Algoritmo SIMPLEX A x b

Princípio de funcionamento do Algoritmo SIMPLEX VB x 1 x 2 x 3 x 4 x 5 x 3 1 0 0 2 x 4 0 1 0 2 x 5 1 1 0 0 1 3 1 2 0 0 0 z PPL na forma canônica: Base é a identidade e coeficientes das VB’s na função objetivo são todos nulos.

Princípio de funcionamento do Algoritmo SIMPLEX VB x 1 x 2 x 3 x 4 x 5 x 3 1 0 0 2 x 4 0 1 0 2 x 5 1 1 0 0 1 3 1 2 0 0 0 z VB = {x 3 = 2, x 4 = 2, x 5 = 2} VNB = {x 1 = 0, x 2 = 0} Solução inicial: x(0) = (0 0 2 2 3)t ; z = 0

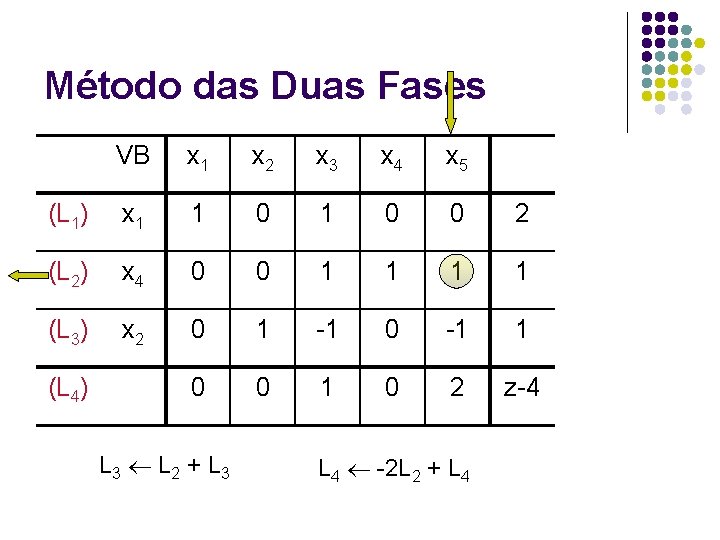
Princípio de funcionamento do Algoritmo SIMPLEX VB x 1 x 2 x 3 x 4 x 5 (L 1) x 3 1 0 0 2 (L 2) x 4 0 1 0 2 (L 3) x 5 1 1 0 0 1 3 1 2 0 0 0 z (L 4) Transformações L 3 -L 2 + L 3 elementares: L 4 -2 L 2 + L 4

Princípio de funcionamento do Algoritmo SIMPLEX VB x 1 x 2 x 3 x 4 x 5 (L 1) x 3 1 0 0 2 (L 2) x 2 0 1 0 2 (L 3) x 5 1 0 0 -1 1 0 0 -2 0 z-4 (L 4) VB = {x 3 = 2, x 2 = 2, x 5 = 1} VNB = {x 1 = 0, x 4 = 0} Final da Iteração 1: x(1) = (0 2 2 0 1)t ; z = 4

Princípio de funcionamento do Algoritmo SIMPLEX VB x 1 x 2 x 3 x 4 x 5 (L 1) x 3 1 0 0 2 (L 2) x 2 0 1 0 2 (L 3) x 5 1 0 0 -1 1 0 0 -2 0 z-4 (L 4) L 1 -L 3 + L 1 L 4 -L 3 + L 4

Princípio de funcionamento do Algoritmo SIMPLEX VB x 1 x 2 x 3 x 4 x 5 (L 1) x 3 0 0 1 1 -1 1 (L 2) x 2 0 1 0 2 (L 3) x 1 1 0 0 -1 1 1 0 0 0 -1 -1 z-5 (L 4) VB = {x 1 = 1, x 2 = 2, x 3 = 1} VNB = {x 4 = 0, x 5 = 0} Final da Iteração 2: x(2) = (1 2 1 0 0)t ; z = 5

Interpretação geométrica x 2 A = (0, 0) B = (2, 0) C = (1, 1) D = (1, 2) E = (0, 2) F = (0, 3) G = (2, 2) H = (3, 0) x 1 2 F E D x 2 2 G C x 1 + x 2 3 A B H x 1

Situação em que a origem não pode ser solução inicial: Exemplo 2 A x b

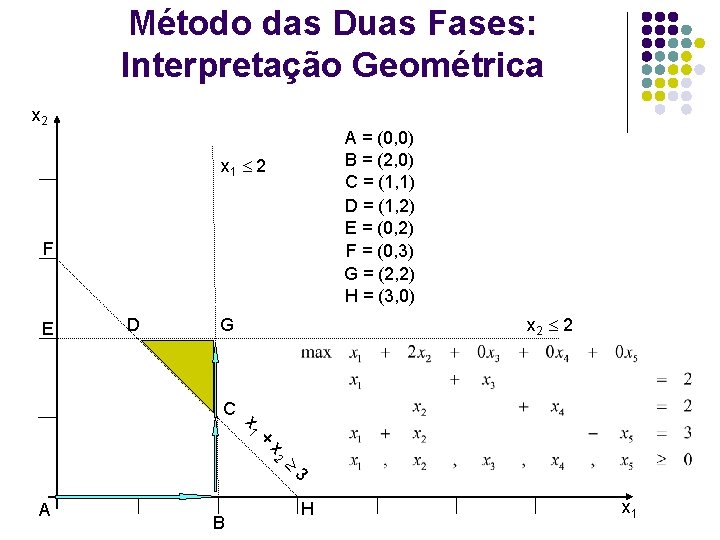
Método das Duas Fases x 2 A = (0, 0) B = (2, 0) C = (1, 1) D = (1, 2) E = (0, 2) F = (0, 3) G = (2, 2) H = (3, 0) x 1 2 F E D x 2 2 G C x 1 + x 2 3 A B H x 1

Método das Duas Fases l Primeira fase (Criar problema auxiliar P’): l l l l Introduzir variáveis de folga e variáveis artificiais Variáveis de folga: introduzidas quando há variáveis do tipo ou Variáveis artificiais: introduzidas quando há restrições do tipo ou = Criar função objetivo artificial: Variáveis básicas iniciais: variáveis de folga associadas às restrições e variáveis artificiais Objetivo da primeira fase: minimizar a função objetivo artificial Caminhar de SBV em SBV de P’ até alcançar SBV do problema original P (situação que ocorre quando todas as variáveis artificiais são nulas).

Método das Duas Fases l Segunda fase: l l A partir de uma SBV do problema original P, gerar SBV cada vez melhores até se atingir a solução ótima. Aplicando o método das duas fases ao PPL dado, tem-se:

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a (L 1) x 3 1 0 0 0 2 (L 2) x 4 0 1 0 0 2 (L 3) x 1 a 1 1 0 0 -1 1 3 (L 4) 0 0 0 1 za (L 5) 1 2 0 0 z Redução à forma canônica: L 4 -L 3 + L 4

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a (L 1) x 3 1 0 0 0 2 (L 2) x 4 0 1 0 0 2 (L 3) x 1 a 1 1 0 0 -1 1 3 (L 4) -1 -1 0 0 1 0 za -3 (L 5) 1 2 0 0 z L 3 -L 1 + L 3 L 4 L 1 + L 4 L 5 -L 1 + L 5

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a (L 1) x 1 1 0 0 0 2 (L 2) x 4 0 1 0 0 2 (L 3) x 1 a 0 1 -1 0 -1 1 1 (L 4) 0 -1 1 0 za -1 (L 5) 0 2 -1 0 0 0 z-2 L 2 -L 3 + L 2 L 4 L 3 + L 4 L 5 -2 L 3 + L 5

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a (L 1) x 1 1 0 0 0 2 (L 2) x 4 0 0 1 1 1 -1 1 (L 3) x 2 0 1 -1 0 -1 1 1 (L 4) 0 0 1 za (L 5) 0 0 1 0 2 -2 z-4 Fim da primeira fase: za = 0 x = (2, 1); z = 4

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 (L 1) x 1 1 0 0 2 (L 2) x 4 0 0 1 1 (L 3) x 2 0 1 -1 0 -1 1 0 0 1 0 2 z-4 (L 4) L 3 L 2 + L 3 L 4 -2 L 2 + L 4

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 (L 1) x 1 1 0 0 2 (L 2) x 5 0 0 1 1 (L 3) x 2 0 1 0 2 0 0 -1 -2 0 z-6 (L 4) Solução ótima: x* = (2, 2); z* = 6

Método das Duas Fases: Interpretação Geométrica x 2 A = (0, 0) B = (2, 0) C = (1, 1) D = (1, 2) E = (0, 2) F = (0, 3) G = (2, 2) H = (3, 0) x 1 2 F E D x 2 2 G C x 1 + x 2 3 A B H x 1

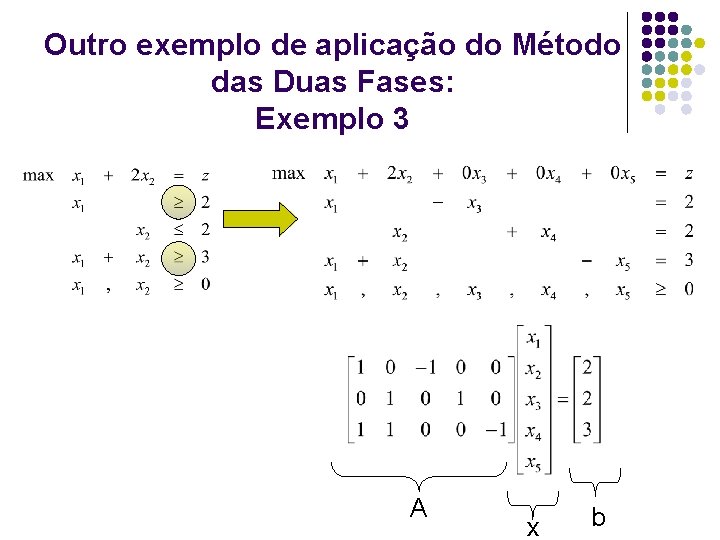
Outro exemplo de aplicação do Método das Duas Fases: Exemplo 3 A x b

Método das Duas Fases: Exemplo 3 l Introduzindo variáveis artificiais no PPL dado, tem -se:

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a x 2 a (L 1) x 1 a 1 0 -1 0 0 1 0 2 (L 2) x 4 0 1 0 0 0 2 (L 3) x 2 a 1 1 0 0 -1 0 1 3 (L 4) 0 0 0 1 1 za (L 5) 1 2 0 0 0 z Transf. para forma canônica: L 4 -L 1 – L 3 + L 4

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a x 2 a (L 1) x 1 a 1 0 -1 0 0 1 0 2 (L 2) x 4 0 1 0 0 0 2 (L 3) x 2 a 1 1 0 0 -1 0 1 3 (L 4) -2 -1 1 0 0 za -5 (L 5) 1 2 0 0 0 z L 3 -L 1 + L 3 L 4 2 L 1 + L 4 L 5 -L 1 + L 5

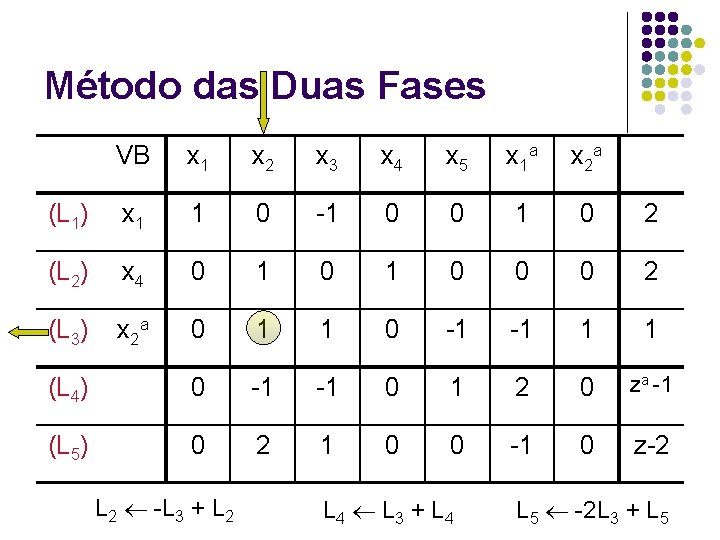
Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a x 2 a (L 1) x 1 1 0 -1 0 0 1 0 2 (L 2) x 4 0 1 0 0 0 2 (L 3) x 2 a 0 1 1 0 -1 -1 1 1 (L 4) 0 -1 -1 0 1 2 0 za -1 (L 5) 0 2 1 0 0 -1 0 z-2 L 2 -L 3 + L 2 L 4 L 3 + L 4 L 5 -2 L 3 + L 5

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a x 2 a (L 1) x 1 1 0 -1 0 0 1 0 2 (L 2) x 4 0 0 -1 1 (L 3) x 2 0 1 1 0 -1 -1 1 1 (L 4) 0 0 0 1 1 za (L 5) 0 0 -1 0 2 1 -2 z-4 Fim da primeira fase: za = 0 x = (2, 1); z = 4

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 (L 1) x 1 1 0 -1 0 0 2 (L 2) x 4 0 0 -1 1 (L 3) x 2 0 1 1 0 -1 1 0 0 -1 0 2 z-4 (L 4) L 3 L 2 + L 3 L 4 -2 L 2 + L 4

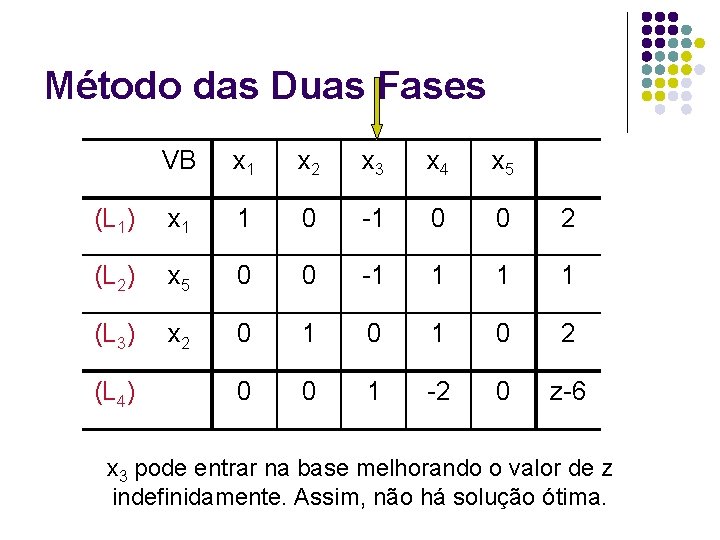
Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 (L 1) x 1 1 0 -1 0 0 2 (L 2) x 5 0 0 -1 1 (L 3) x 2 0 1 0 2 0 0 1 -2 0 z-6 (L 4) x 3 pode entrar na base melhorando o valor de z indefinidamente. Assim, não há solução ótima.

Método das Duas Fases: Interpretação Geométrica x 2 A = (0, 0) B = (2, 0) C = (1, 1) D = (1, 2) E = (0, 2) F = (0, 3) G = (2, 2) H = (3, 0) x 1 2 F E D x 2 2 G C x 1 + x 2 3 A B H x 1

Método das Duas Fases: Exemplo 4 A x b

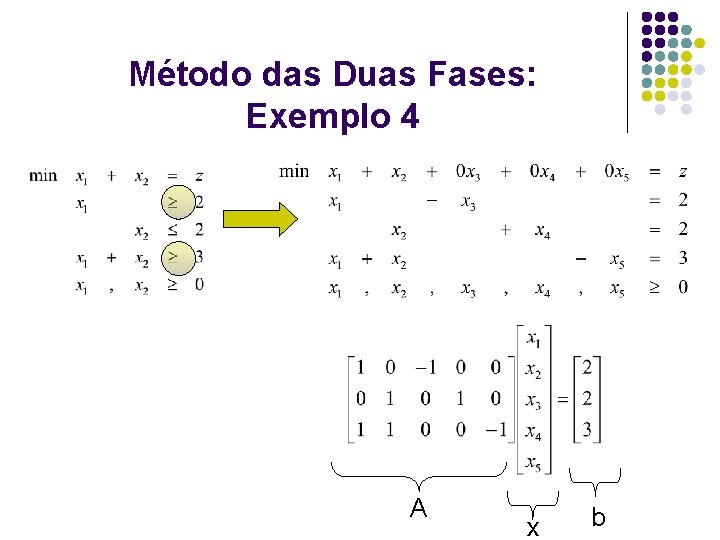
Método das Duas Fases: Exemplo 4 l Introduzindo variáveis artificiais no PPL dado, tem -se:

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a x 2 a (L 1) x 1 a 1 0 -1 0 0 1 0 2 (L 2) x 4 0 1 0 0 0 2 (L 3) x 2 a 1 1 0 0 -1 0 1 3 (L 4) 0 0 0 1 1 za (L 5) 1 1 0 0 0 z Transf. para forma canônica: L 4 -L 1 – L 3 + L 4

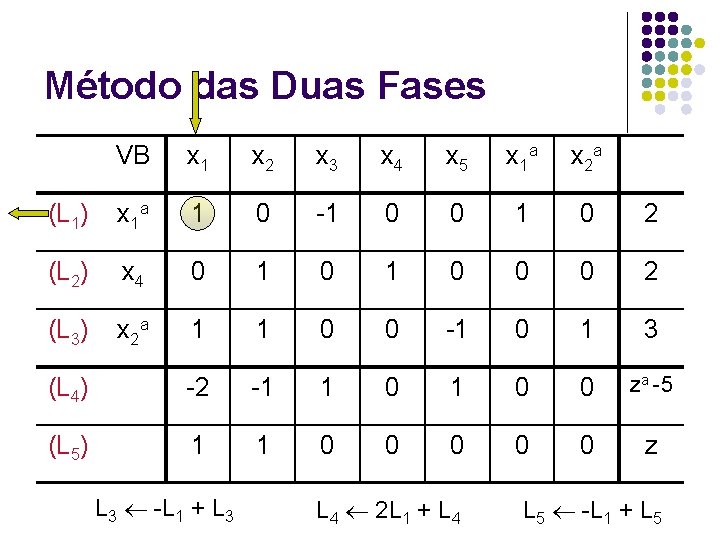
Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a x 2 a (L 1) x 1 a 1 0 -1 0 0 1 0 2 (L 2) x 4 0 1 0 0 0 2 (L 3) x 2 a 1 1 0 0 -1 0 1 3 (L 4) -2 -1 1 0 0 za -5 (L 5) 1 1 0 0 0 z L 3 -L 1 + L 3 L 4 2 L 1 + L 4 L 5 -L 1 + L 5

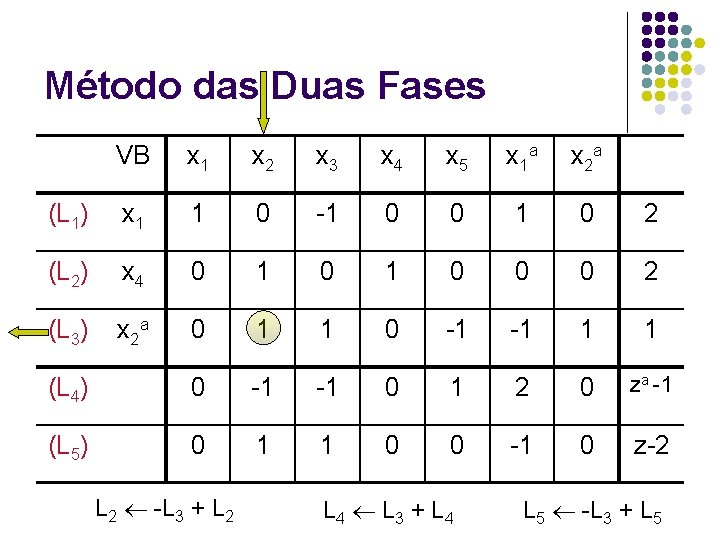
Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a x 2 a (L 1) x 1 1 0 -1 0 0 1 0 2 (L 2) x 4 0 1 0 0 0 2 (L 3) x 2 a 0 1 1 0 -1 -1 1 1 (L 4) 0 -1 -1 0 1 2 0 za -1 (L 5) 0 1 1 0 0 -1 0 z-2 L 2 -L 3 + L 2 L 4 L 3 + L 4 L 5 -L 3 + L 5

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 x 1 a x 2 a (L 1) x 1 1 0 -1 0 0 1 0 2 (L 2) x 4 0 0 -1 1 (L 3) x 2 0 1 1 0 -1 -1 1 1 (L 4) 0 0 0 1 1 za (L 5) 0 0 1 1 -1 z-3 Fim da primeira fase: za = 0 x = (2, 1); z = 3

Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 (L 1) x 1 1 0 -1 0 0 2 (L 2) x 4 0 0 -1 1 (L 3) x 2 0 1 1 0 -1 1 0 0 1 z-3 (L 4) Solução ótima: z = 3; x 1 = 2; x 2 = 1; x 3 é VNB nula L 1 L 3 + L 1 L 2 L 3 + L 2

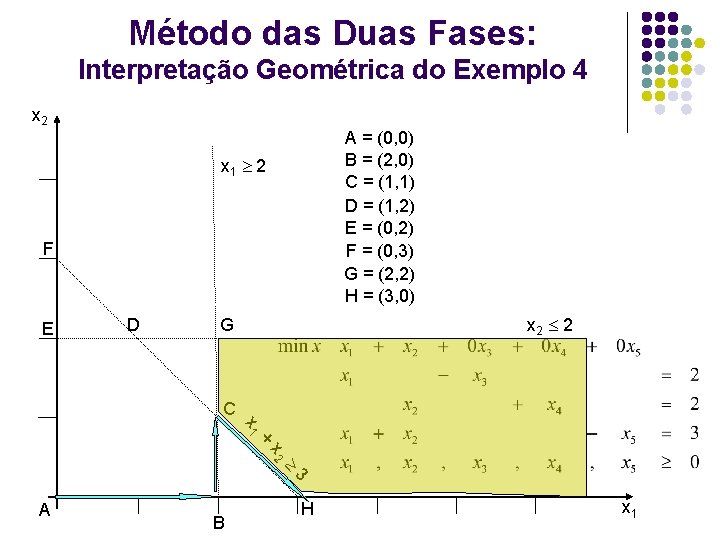
Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 (L 1) x 1 1 1 0 0 -1 3 (L 2) x 4 0 1 0 2 (L 3) x 3 0 1 1 0 -1 1 0 0 1 z-3 (L 4) Outra solução ótima: z = 3; x 1 = 3; x 2 = 0

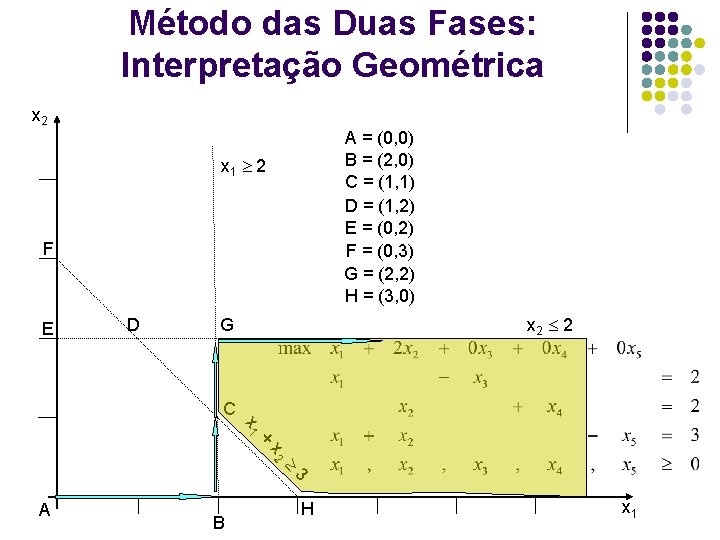
Método das Duas Fases VB x 1 x 2 x 3 x 4 x 5 (L 1) x 1 1 1 0 0 -1 3 (L 2) x 4 0 1 0 2 (L 3) x 3 0 1 1 0 -1 1 0 0 1 z-3 (L 4) Assim, todos os pontos da aresta que liga os pontos (2, 1) e (3, 0) são ótimos. Isto é, todos os pontos da forma: x* = (x 1 , x 2) = (2, 1) + (1 - ) (3, 0), sendo [0, 1]

Método das Duas Fases: Interpretação Geométrica do Exemplo 4 x 2 A = (0, 0) B = (2, 0) C = (1, 1) D = (1, 2) E = (0, 2) F = (0, 3) G = (2, 2) H = (3, 0) x 1 2 F E D x 2 2 G C x 1 + x 2 3 A B H x 1

Dualidade l Seja o PPL, doravante chamado de PPL primal: l ou, na forma expandida:

Dualidade l Associado a este PPL, existe um PPL, chamado PPL dual: l ou, na forma expandida:

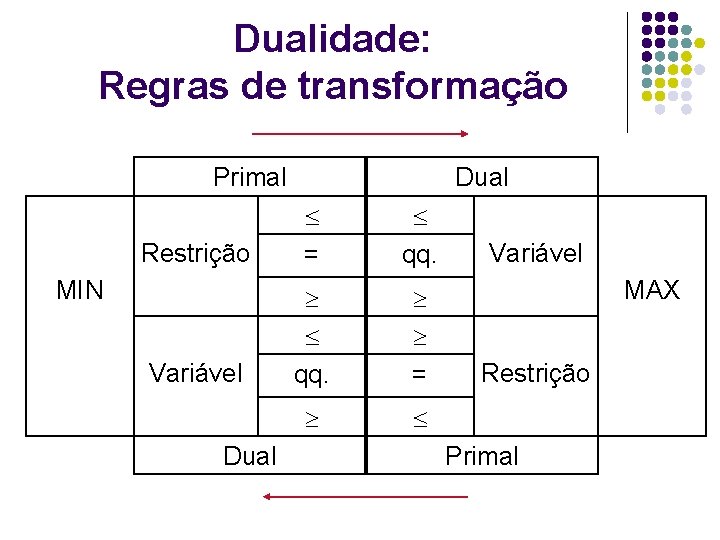
Dualidade: Regras de transformação Primal Dual Restrição = qq. Variável qq. = MIN Dual Variável MAX Restrição Primal

Dualidade: Vantagens l Em situações na qual a matriz de coeficientes do primal tem maior número de linhas do que de colunas: Dual A base no DUAL é menor!!!

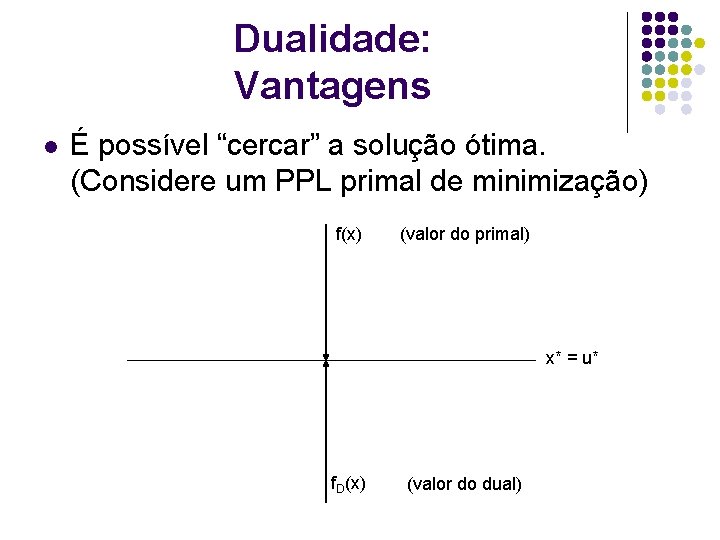
Dualidade: Vantagens l É possível “cercar” a solução ótima. (Considere um PPL primal de minimização) f(x) (valor do primal) x* = u* f. D(x) (valor do dual)

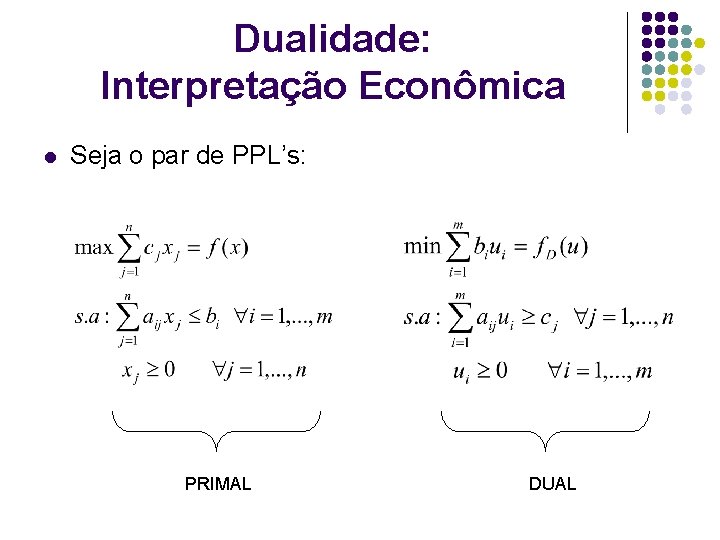
Dualidade: Interpretação Econômica l Seja o par de PPL’s: PRIMAL DUAL

Dualidade: Interpretação Econômica l Sejam x* e u* soluções ótimas desses PPL’s e seja B* a base relativa a essas soluções. Então: l Supondo b variável e derivando em relação a b, temos: l Então u* é a taxa de variação do valor ótimo da função objetivo f(x*) com b. Como u* 0, então f(x*) cresce à medida que bi cresce

Dualidade: Interpretação Econômica l l l Considere o primal um problema de alocação de recursos, com m recursos disponíveis nas quantidades b 1, b 2, . . . , bm com os quais desejamos fabricar n produtos nas quantidades x 1, x 2, . . . , xn a serem determinadas. Cada unidade do produto j consome aij unidades do recurso i trazendo um retorno de cj unidades monetárias. Queremos determinar a quantidade a ser fabricada de cada produto de modo a maximizar o retorno.

Dualidade: Interpretação Econômica l l Suponha, agora, aumentada em uma unidade a quantidade disponível do recurso k, isto é, temos (bk + 1) unidades. Suponha que a base associada permaneça a mesma. Neste caso, a nova solução ótima u** do dual permanece a mesma uma vez que: u** = u* = (c. B*)t. B*-1. A nova solução ótima x** será:

Dualidade: Interpretação Econômica l l Isto é, f(x**) – f(x*) = uk*, ou seja, uk* é o incremento no lucro trazido pelo aumento de uma unidade da matéria disponível k. uk* é chamado shadow price, dual, valor incremental, efficiency price, valor implícito, etc.

Análise de Sensibilidade (Pós-otimização) l l Seja o sistema Ax=b, com uma base B, e uma função objetivo f(x) Seja o quadro genérico do Simplex em uma dada iteração colocado na forma matricial não canônica (x. R)t (x. B)t (L 1) (L 2) x. B R B b (c. R)t (c. B)t f(x)

Análise de Sensibilidade (Pós-otimização) l Para colocar esse quadro na forma canônica devemos efetuar as seguintes transformações elementares: L 1 B-1 L 1 (x. R)t (x. B)t (L 1) (L 2) x. B BI B-1 b 1 R (c. R)t (c. B)t f(x) L 2 -(c. B)t L 1+ L 2

Análise de Sensibilidade (Pós-otimização) (L 1) (x. R)t (x. B)t B-1 R I B-1 b (c. R)t - (c. B)t. B-1 R (0)t f(x)-(c. B)t. B-1 b x. B (L 2) Seja: Y = B-1 R yj = B-1 aj x. B = B-1 b z = (c. B)t. B-1 R zj = (c. B)t. B-1 aj

Análise de Sensibilidade (Pós-otimização) (L 1) (L 2) x. B (x. R)t (x. B)t Y I x. B (c. R)t - z (0)t f(x)-f(x) Sendo: f(x) = ctx = (c. B)tx. B + (c. R)tx. R = = (c. B)tx. B = (c. B)t. B-1 b

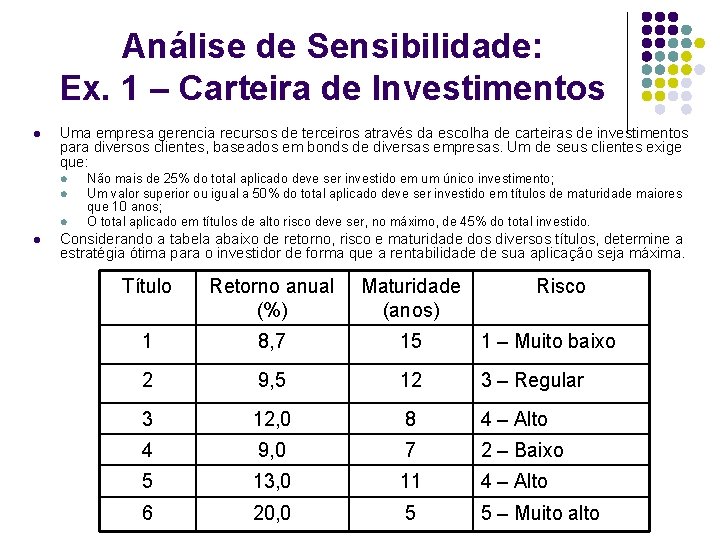
Análise de Sensibilidade: Ex. 1 – Carteira de Investimentos l Uma empresa gerencia recursos de terceiros através da escolha de carteiras de investimentos para diversos clientes, baseados em bonds de diversas empresas. Um de seus clientes exige que: l l Não mais de 25% do total aplicado deve ser investido em um único investimento; Um valor superior ou igual a 50% do total aplicado deve ser investido em títulos de maturidade maiores que 10 anos; O total aplicado em títulos de alto risco deve ser, no máximo, de 45% do total investido. Considerando a tabela abaixo de retorno, risco e maturidade dos diversos títulos, determine a estratégia ótima para o investidor de forma que a rentabilidade de sua aplicação seja máxima. Título Retorno anual (%) Maturidade (anos) Risco 1 8, 7 15 1 – Muito baixo 2 9, 5 12 3 – Regular 3 12, 0 8 4 – Alto 4 9, 0 7 2 – Baixo 5 13, 0 11 4 – Alto 6 20, 0 5 5 – Muito alto

Carteira de Investimentos: Modelo de Programação Matemática

Análise de sensibilidade: Carteira de Investimentos - Questões 1. 2. 3. 4. 5. Qual o melhor retorno que se pode obter? Quanto se deve aplicar em cada título para que se tenha o retorno ótimo? Em qual percentual aumentaria o retorno se fosse permitido aplicar 1% a mais no Título 2? De quanto seria o retorno? Essa regra vale até quanto? A partir de qual percentual a aplicação no título 3 é vantajosa? Se fosse imposto limitar a aplicação em cada título em 24% para um dentre os títulos 2, 4 e 6, em qual título deveria ser feita a diminuição de aplicação? Justifique. Quanto está influenciando a restrição de limitação de aplicação em título de alto risco? Qual seria o retorno se esta limitação fosse de 49%?

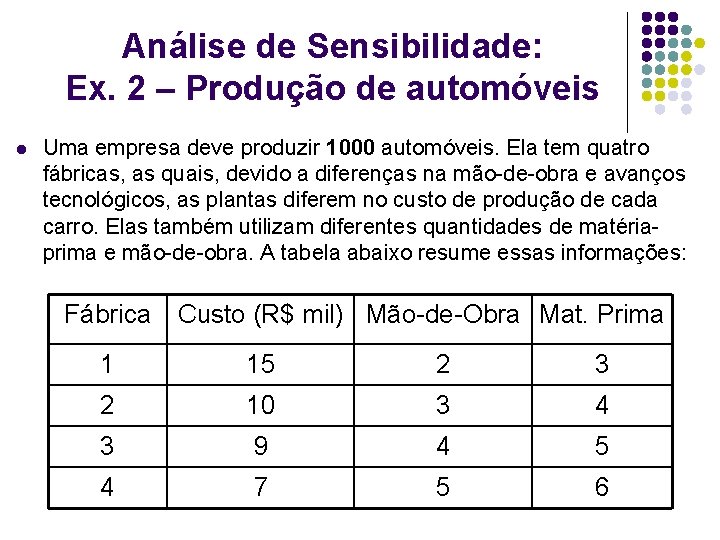
Análise de Sensibilidade: Ex. 2 – Produção de automóveis l Uma empresa deve produzir 1000 automóveis. Ela tem quatro fábricas, as quais, devido a diferenças na mão-de-obra e avanços tecnológicos, as plantas diferem no custo de produção de cada carro. Elas também utilizam diferentes quantidades de matériaprima e mão-de-obra. A tabela abaixo resume essas informações: Fábrica Custo (R$ mil) Mão-de-Obra Mat. Prima 1 15 2 3 2 10 3 4 3 9 4 5 4 7 5 6

Análise de Sensibilidade Ex. 2 – Produção de automóveis l Um acordo trabalhista requer que pelo menos 400 carros sejam produzidos na fábrica 3. Existem 3300 horas de mão-de-obra e 4000 unidades de material que podem ser alocas às 4 fábricas. O modelo de programação matemática que otimiza a produção é:

Análise de sensibilidade: Ex. 2 – Produção de automóveis 1. 2. 3. 4. 5. 6. 7. Quais são as quantias ótimas de produção? Qual o custo da produção? Quanto custa produzir mais um veículo? Quanto economizamos produzindo um veículo a menos? Como mudaria a solução se custasse somente R$8. 000, 00 para produzir na fábrica 2? Como ficaria o custo? Quanto estamos dispostos a pagar por uma hora de trabalho? Quanto o acordo está custando? Qual seria a variação no custo se o acordo fosse de 250 carros? Quanto vale a matéria-prima (conseguir mais uma unidade)? Quantas unidades estamos dispostos a pagar por esse preço? Até que custo ainda é vantajoso produzir na fábrica 2?